2.1.1合情推理
图片预览








文档简介
课件37张PPT。推理与证明推理证明言之有理,论证有据!第二章 推理与证明已知的判断新的判断 根据一个或几个已知的判断来确定一个新的判断的思维过程就叫推理.32.1.1合情推理 佛教《百喻经》中有这样一则故事。 从前有一位富翁想吃芒果,打发他的仆人到果园去买,并告诉他:"要甜的,好吃的,你才买."仆人拿好钱就去了.到了果园,园主说:"我这里树上的芒果个个都是甜的,你尝一个看."仆人说:"我尝一个怎能知道全体呢 我应当个个都尝过,尝一个买一个,这样最可靠."仆人于是自己动手摘芒果,摘一个尝一口,甜的就都买回去.带回家去,富翁见了,觉得非常恶心,一齐都扔了.第一个芒果是甜的第二个芒果是甜的第三个芒果是甜的这个果园的芒果都是甜的10= 3+7
20= 3+17
30= 13+17 ——哥德巴赫猜想铜能导电
铝能导电
金能导电
银能导电三角形内角和
为
凸四边形内角
和为
凸五边形内角
和为
第一个芒果是甜的
第二个芒果是甜的
第三个芒果是甜的第一个数为2
第二个数为4
第三个数为6
第四个数为8
部分
个别整 体
一 般 由某类事物的 具有某些特征,
推出该类事物的 都具有这些特征
的推理,或者由 概括出
的推理,称为归纳推理(简称归纳).部分对象全部对象个别事实一般结论归纳推理归纳推理的基础归纳推理的作用归纳推理观察、分析发现新事实、获得新结论由部分到整体、
个别到一般的推理注意归纳推理的结论不一定成立成语“一叶知秋”统计初步中的用样本估计总体 通过从总体中抽取部分对象进
行观测或试验,进而对整体做出推断. 意思是从一片树叶的凋落,知道秋
天将要来到.比喻由细微的迹象看出整体
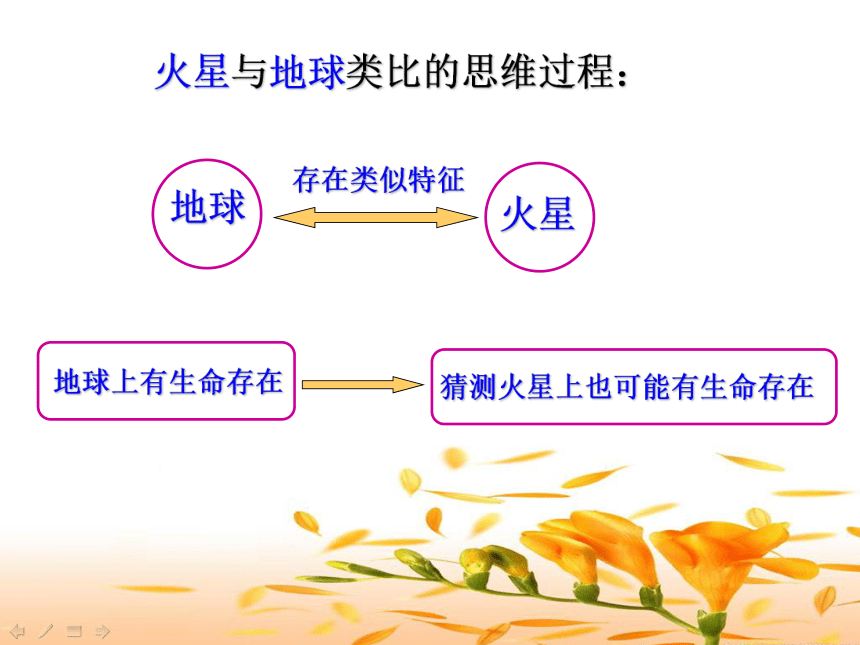
形势的变化,由部分推知全体.可能有生命存在有生命存在温度适合生物的生存一年中有四季的变更有大气层行星、围绕太阳运行、绕轴自转火星地球火星上是否存在生命火星与地球类比的思维过程:火星地球存在类似特征 我国古代工匠鲁班类比带齿的草叶和蝗虫的牙齿,发明了锯;人们仿照鱼类的外型和它们在水中沉浮的原理,发明了潜水艇.
仿生学中许多发明的最初构想
都是类比生物机制得到的. 苍蝇的楫翅(又叫平衡棒)是“天然导航仪”,
人们模仿它制成了“振动陀螺仪”.这种仪器目前已
经应用在火箭和高速飞机上,实现了自动驾驶。
苍蝇的眼睛是一种“复眼”,由3000多只小眼
组成,人们模仿它制成了“蝇眼透镜” ,一次就能
照出千百张相同的相片。 由两类对象具有某些类似特征和其中
一类对象的某些已知特征,推出另一类对
象也具有这些特征的推理称为类比推理.类比推理简言之,类比推理是由特殊到特殊的推理.在研究球体时,自然联想到圆.探究:类比圆的特征,说说球的相关特征,并说明推理的过程。试将平面上的圆与空间的球进行类比.圆的定义:平面内到一个定点的距离等于定长的点的集合球的定义:空间中到一个定点的距离等于定长的点的集合圆
弦
直径周长
面积球
截面圆大圆表面积体积15圆的概念和性质球的概念和性质与圆心距离相等的两弦相等与圆心距离不相等的两弦不相等,距圆心较近的弦较长以点(x0,y0)为圆心, r为半径的圆的方程为(x-x0)2+(y-y0)2 = r2圆心与弦(非直径)中点的连线垂直于弦球心与不过球心的截面(圆面)的圆心的连线垂直于截面与球心距离相等的两截面面积相等与球心距离不相等的两截面面积不相等,距球心较近的面积较大以点(x0,y0,z0)为球心, r为半径的球的方程为(x-x0)2+(y-y0)2+(z-z0)2 = r2利用圆的性质类比得出求的性质球的体积球的表面积圆的周长 圆的面积16 在数学中,由已经解决的问题和已经获得的知识出发,通过类比而提出新问题和作出新发现.如:立体几何与平面几何的类比向量与数的类比无限与有限的类比不等与相等的类比……17例1 类比实数的加法和乘法,列出它们相似的运算性质.Rab=ba
(ab)c=a(bc)ax=1(a≠0)
x=1/a
1*a=a18等差数列{an}中①an= am+(n-m)d③若m+n=p+q,
则am+an=ap+aq④若 p+q=2n,ap+ aq= 2an②等比数列{an}中①an= am· qn-m③若m+n=p+q,
则am·an=ap·aq④若 p+q=2n,ap· aq= an2② an÷ am= qn-m概念
性
质
差商相似点:都是相邻两项的关系,都为常数和积例2.19例3:试根据等式的性质猜想不等式的性质.等 式不等式(1) a=b a+c=b+ca>b a+c>b+c(2) a=b ac=bca>b ac>bca>b a2>b2(3) a=b a2=b2等等解:等式与不等式有不少相似的属性,例如:问:这样猜想出的结论是否一定正确?分析:面积法2121ABCDOO2222例5:类比平面内直角三角形的勾股定理,试给出空间中四面体性质的猜想.s1s2s3c2=a2+b2平面图形(二维)立体图形(三维)点点或线线线或面平面直角坐标系空间直角坐标系 运用类比法的关键是:周长面积面积体积2424我们要根据实际情况选择适当的类比对象.如:平 面空 间正方形正方体圆球三角形三棱锥注意:进行类比
时,合理地确定
类比对象是非常
重要的,否则会
使类比成为“乱比”25长方体空间向量复数我们要根据实际情况选择适当的类比对象.平 面空 间注意:进行类比
时,合理地确定
类比对象是非常
重要的,否则会
使类比成为“乱比”正方形正方体圆球三角形三棱锥类比推理的几个特点;1.类比是从人们已经掌握了的事物的属性,推测正在研究的事物的属性,是以旧有的认识为基础,类比出新的结果.2.类比是从一种事物的特殊属性推测另一种事物的特殊属性.3.类比的结果是猜测性的不一定可靠,单它却有发现的功能.类比推理类比推理
以旧的知识为基础,推测新的结果,具有发现的功能
由特殊到特殊的推理类比推理的结论不一定成立注意我们已经学习过“等差数列”与“等比数列”.你是否想过“等和数列”、“等积数列” ?类比推理由特殊到特殊的推理;以旧的知识为基础,推测新的结果;结论不一定成立.归纳推理由部分到整体、特殊到一般的推理;以观察分析为基础,推测新的结论;具有发现的功能;结论不一定成立.具有发现的功能;归纳推理和类比推理的过程通俗地说,合情推理是指“合乎情理”的推理. 传说中开天辟地的神勃拉玛在古老的印度贝拿勒斯的神庙中留下了三根针和套在一根针上的64个圆环.神指示他的僧侣们按下列规则,把圆环从一根针上全部移到另一根针上,第三根针起“过渡”的作用.
1.每次只能移动1个圆环;
2.较大的圆环不能放在较小的圆环上面.
如果有一天,僧侣们将这64个圆环全部移到另一根针上,那么世界末日就来临了.
请你试着推测:把 个圆环从1号针移到3号针,最少需要移动多少次?123游戏:河内塔(Tower of Hanoi)123第1个圆环从1到3.设 为把 个圆环从1号针移到3号针的最少次数,则 =1时, =1 =2时,123第1个圆环从1到3.前1个圆环从1到2;
第2个圆环从1到3;
第1个圆环从2到3.设 为把 个圆环从1号针移到3号针的最少次数,则 =1 =1时, =3 =2时, =3 =1时, =1 =3时,123第1个圆环从1到3.前1个圆环从1到2;
第2个圆环从1到3;
前1个圆环从2到3.前2个圆环从1到2;
第3个圆环从1到3;
前2个圆环从2到3.设 为把 个圆环从1号针移到3号针的最少次数,则 =7一年有多少秒?( 60×60×24×365)秒
需要多少年?[18446744073709511615÷ (60×60×24×365)] ≈5846亿年善于观察勤于思考敢于猜想的人常常会冒出创造的灵感火花合情推理是地球上
最美丽的思维花朵之一!37
20= 3+17
30= 13+17 ——哥德巴赫猜想铜能导电
铝能导电
金能导电
银能导电三角形内角和
为
凸四边形内角
和为
凸五边形内角
和为
第一个芒果是甜的
第二个芒果是甜的
第三个芒果是甜的第一个数为2
第二个数为4
第三个数为6
第四个数为8
部分
个别整 体
一 般 由某类事物的 具有某些特征,
推出该类事物的 都具有这些特征
的推理,或者由 概括出
的推理,称为归纳推理(简称归纳).部分对象全部对象个别事实一般结论归纳推理归纳推理的基础归纳推理的作用归纳推理观察、分析发现新事实、获得新结论由部分到整体、
个别到一般的推理注意归纳推理的结论不一定成立成语“一叶知秋”统计初步中的用样本估计总体 通过从总体中抽取部分对象进
行观测或试验,进而对整体做出推断. 意思是从一片树叶的凋落,知道秋
天将要来到.比喻由细微的迹象看出整体
形势的变化,由部分推知全体.可能有生命存在有生命存在温度适合生物的生存一年中有四季的变更有大气层行星、围绕太阳运行、绕轴自转火星地球火星上是否存在生命火星与地球类比的思维过程:火星地球存在类似特征 我国古代工匠鲁班类比带齿的草叶和蝗虫的牙齿,发明了锯;人们仿照鱼类的外型和它们在水中沉浮的原理,发明了潜水艇.
仿生学中许多发明的最初构想
都是类比生物机制得到的. 苍蝇的楫翅(又叫平衡棒)是“天然导航仪”,
人们模仿它制成了“振动陀螺仪”.这种仪器目前已
经应用在火箭和高速飞机上,实现了自动驾驶。
苍蝇的眼睛是一种“复眼”,由3000多只小眼
组成,人们模仿它制成了“蝇眼透镜” ,一次就能
照出千百张相同的相片。 由两类对象具有某些类似特征和其中
一类对象的某些已知特征,推出另一类对
象也具有这些特征的推理称为类比推理.类比推理简言之,类比推理是由特殊到特殊的推理.在研究球体时,自然联想到圆.探究:类比圆的特征,说说球的相关特征,并说明推理的过程。试将平面上的圆与空间的球进行类比.圆的定义:平面内到一个定点的距离等于定长的点的集合球的定义:空间中到一个定点的距离等于定长的点的集合圆
弦
直径周长
面积球
截面圆大圆表面积体积15圆的概念和性质球的概念和性质与圆心距离相等的两弦相等与圆心距离不相等的两弦不相等,距圆心较近的弦较长以点(x0,y0)为圆心, r为半径的圆的方程为(x-x0)2+(y-y0)2 = r2圆心与弦(非直径)中点的连线垂直于弦球心与不过球心的截面(圆面)的圆心的连线垂直于截面与球心距离相等的两截面面积相等与球心距离不相等的两截面面积不相等,距球心较近的面积较大以点(x0,y0,z0)为球心, r为半径的球的方程为(x-x0)2+(y-y0)2+(z-z0)2 = r2利用圆的性质类比得出求的性质球的体积球的表面积圆的周长 圆的面积16 在数学中,由已经解决的问题和已经获得的知识出发,通过类比而提出新问题和作出新发现.如:立体几何与平面几何的类比向量与数的类比无限与有限的类比不等与相等的类比……17例1 类比实数的加法和乘法,列出它们相似的运算性质.Rab=ba
(ab)c=a(bc)ax=1(a≠0)
x=1/a
1*a=a18等差数列{an}中①an= am+(n-m)d③若m+n=p+q,
则am+an=ap+aq④若 p+q=2n,ap+ aq= 2an②等比数列{an}中①an= am· qn-m③若m+n=p+q,
则am·an=ap·aq④若 p+q=2n,ap· aq= an2② an÷ am= qn-m概念
性
质
差商相似点:都是相邻两项的关系,都为常数和积例2.19例3:试根据等式的性质猜想不等式的性质.等 式不等式(1) a=b a+c=b+ca>b a+c>b+c(2) a=b ac=bca>b ac>bca>b a2>b2(3) a=b a2=b2等等解:等式与不等式有不少相似的属性,例如:问:这样猜想出的结论是否一定正确?分析:面积法2121ABCDOO2222例5:类比平面内直角三角形的勾股定理,试给出空间中四面体性质的猜想.s1s2s3c2=a2+b2平面图形(二维)立体图形(三维)点点或线线线或面平面直角坐标系空间直角坐标系 运用类比法的关键是:周长面积面积体积2424我们要根据实际情况选择适当的类比对象.如:平 面空 间正方形正方体圆球三角形三棱锥注意:进行类比
时,合理地确定
类比对象是非常
重要的,否则会
使类比成为“乱比”25长方体空间向量复数我们要根据实际情况选择适当的类比对象.平 面空 间注意:进行类比
时,合理地确定
类比对象是非常
重要的,否则会
使类比成为“乱比”正方形正方体圆球三角形三棱锥类比推理的几个特点;1.类比是从人们已经掌握了的事物的属性,推测正在研究的事物的属性,是以旧有的认识为基础,类比出新的结果.2.类比是从一种事物的特殊属性推测另一种事物的特殊属性.3.类比的结果是猜测性的不一定可靠,单它却有发现的功能.类比推理类比推理
以旧的知识为基础,推测新的结果,具有发现的功能
由特殊到特殊的推理类比推理的结论不一定成立注意我们已经学习过“等差数列”与“等比数列”.你是否想过“等和数列”、“等积数列” ?类比推理由特殊到特殊的推理;以旧的知识为基础,推测新的结果;结论不一定成立.归纳推理由部分到整体、特殊到一般的推理;以观察分析为基础,推测新的结论;具有发现的功能;结论不一定成立.具有发现的功能;归纳推理和类比推理的过程通俗地说,合情推理是指“合乎情理”的推理. 传说中开天辟地的神勃拉玛在古老的印度贝拿勒斯的神庙中留下了三根针和套在一根针上的64个圆环.神指示他的僧侣们按下列规则,把圆环从一根针上全部移到另一根针上,第三根针起“过渡”的作用.
1.每次只能移动1个圆环;
2.较大的圆环不能放在较小的圆环上面.
如果有一天,僧侣们将这64个圆环全部移到另一根针上,那么世界末日就来临了.
请你试着推测:把 个圆环从1号针移到3号针,最少需要移动多少次?123游戏:河内塔(Tower of Hanoi)123第1个圆环从1到3.设 为把 个圆环从1号针移到3号针的最少次数,则 =1时, =1 =2时,123第1个圆环从1到3.前1个圆环从1到2;
第2个圆环从1到3;
第1个圆环从2到3.设 为把 个圆环从1号针移到3号针的最少次数,则 =1 =1时, =3 =2时, =3 =1时, =1 =3时,123第1个圆环从1到3.前1个圆环从1到2;
第2个圆环从1到3;
前1个圆环从2到3.前2个圆环从1到2;
第3个圆环从1到3;
前2个圆环从2到3.设 为把 个圆环从1号针移到3号针的最少次数,则 =7一年有多少秒?( 60×60×24×365)秒
需要多少年?[18446744073709511615÷ (60×60×24×365)] ≈5846亿年善于观察勤于思考敢于猜想的人常常会冒出创造的灵感火花合情推理是地球上
最美丽的思维花朵之一!37
