数列[上学期]
图片预览








文档简介
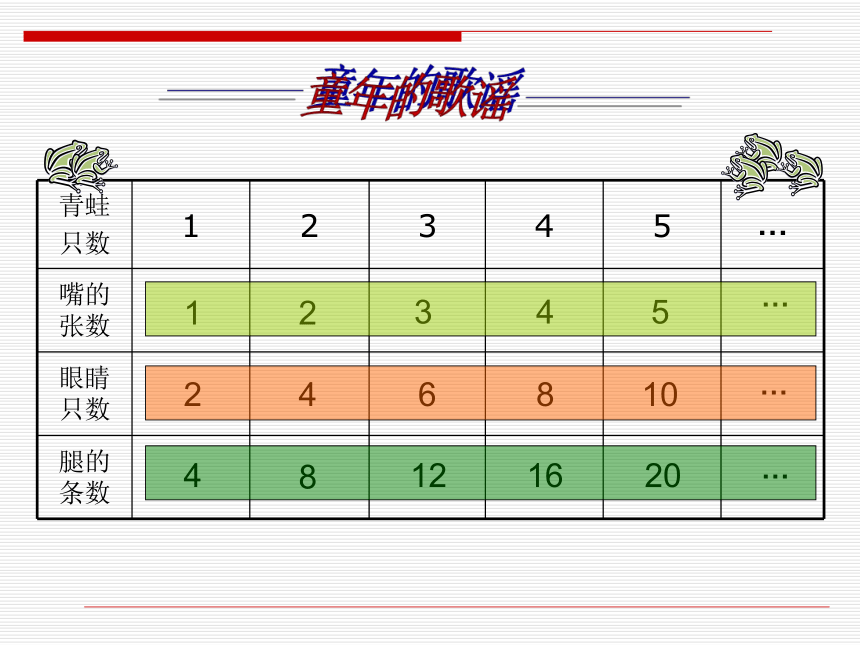
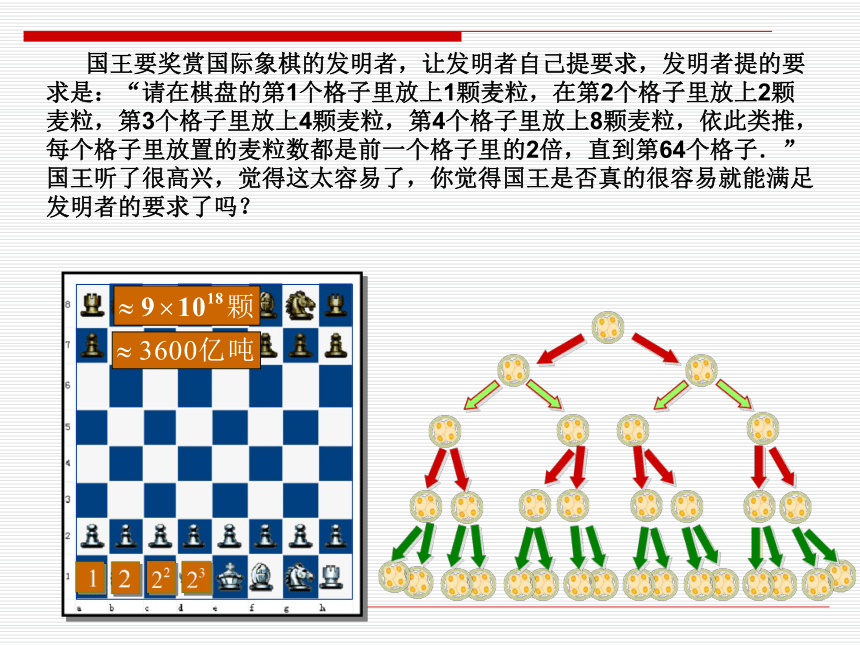
课件33张PPT。数 列数 列全日制普通高级中学教科书(必修)第一册(上)1242483612481651020………童年的歌谣 国王要奖赏国际象棋的发明者,让发明者自己提要求,发明者提的要求是:“请在棋盘的第1个格子里放上1颗麦粒,在第2个格子里放上2颗麦粒,第3个格子里放上4颗麦粒,第4个格子里放上8颗麦粒,依此类推,每个格子里放置的麦粒数都是前一个格子里的2倍,直到第64个格子.”国王听了很高兴,觉得这太容易了,你觉得国王是否真的很容易就能满足发明者的要求了吗?15516162832…数列数列序号n 1 2 3 4 5 …项 an 2 4 6 8 10 ……2×12×22×32×42×5数列数列练习1.根据下面数列的通项公式,写出它的前5项:试判断 是否在数列(1)中?数列练习2.写出下面数列的一个通项公式,使它的前4项分别是下列各数:数列序号n 1 2 3 4 5 …项 an 2 4 6 8 10 ……2×12×22×32×42×5数列是按照项的序号排列的一列函数值数列的图象数列的图象 假设一对刚出生的小兔一个月就能长成大兔,再过一个月便能生下一对小兔,并且此后每个月都生一对小兔,如果没有发生死亡,按逐月计算,每个月初的兔子对数构成如下数列
1,1,2,3,5,8,13,21,34….
这就是为以意大利著名数学家裴波那契命名的“裴波那契数列” .有趣的兔子数列裴波那契螺旋http://www.wxws.cn欢迎各位领导和同行指导数列的概念和简单表示, 26318446744073709551615陛下国库里的麦子不够啊!OK?某种细胞的分裂(1)传说中棋盘上麦粒数按放置的先后排成的一列数:
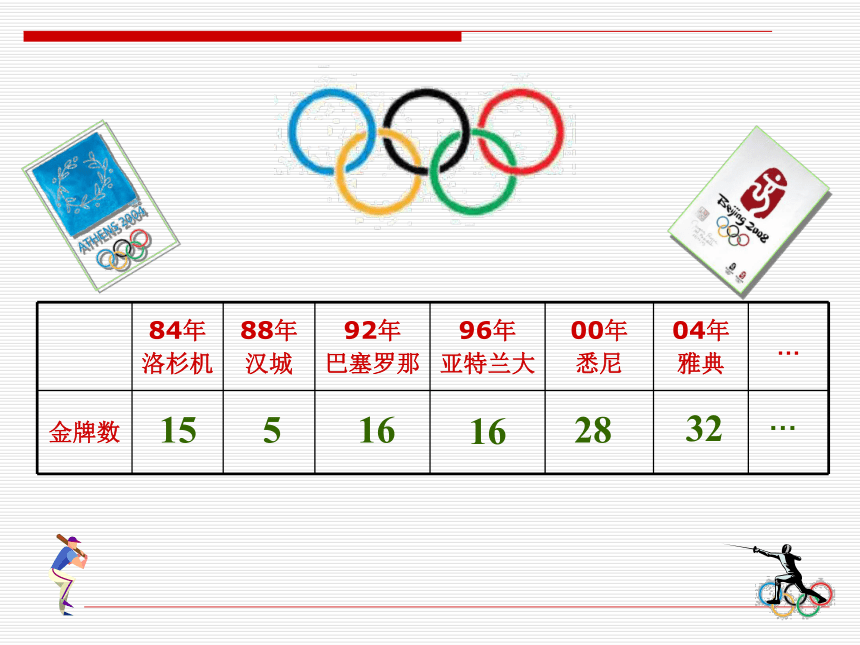
1,2,2 2,2 3,…,2 63(2)某种细胞分裂问题:1,2,4,8,16,…(6)从1984年到今年,我国体育健儿共参加了6次奥运会,获得的金牌数依次排成一列数: 15,5,16,16,28,32(3)π 精确到0.01,0.001,0.0001…的不足近似值排成一列数:3.14,3.141,3.1415,3.14159,3.141592…(5)某剧场有10排座位,第一排有20个座位,后一排都比前一排多2个,则各排的座位数依次为:20,22,24,26,…,38(4)人们在1740年发现了一颗彗星,并推算出它每隔83年出现一次,则从出现那次算起,这颗彗星出现的年份依次为1740,1823,1906,1989, …1、均是一列数,2、有一定次序.观察上面6个例子它们有什么共同特点?特点:(1)1,2,2 2,2 3,…,2 63(2)1,2,4,8,16,…(6)15,5,16,16,28,32(3)(5)20,22,24,26,28,…,38(4)1740,1823,1906,1989, …3.14,3.141,3.1415,3.14159,3.141592…★按一定次序排列的一列数叫数列.
定义★数列中的每一个数叫做这个数列的项.★项数有限的数列叫做有穷数列; 项数无限的数列叫做无穷数列.各项依次叫做这个数列的第1项(首项)、第2项、…、第n项…问题2: -1,1,-1,1是否是一数列?问题1: 数列:1,2,3,4,5
数列:5,4,3,2,1
它们是否是同一数列?
问题3: 数列中的项和集合中的 元素
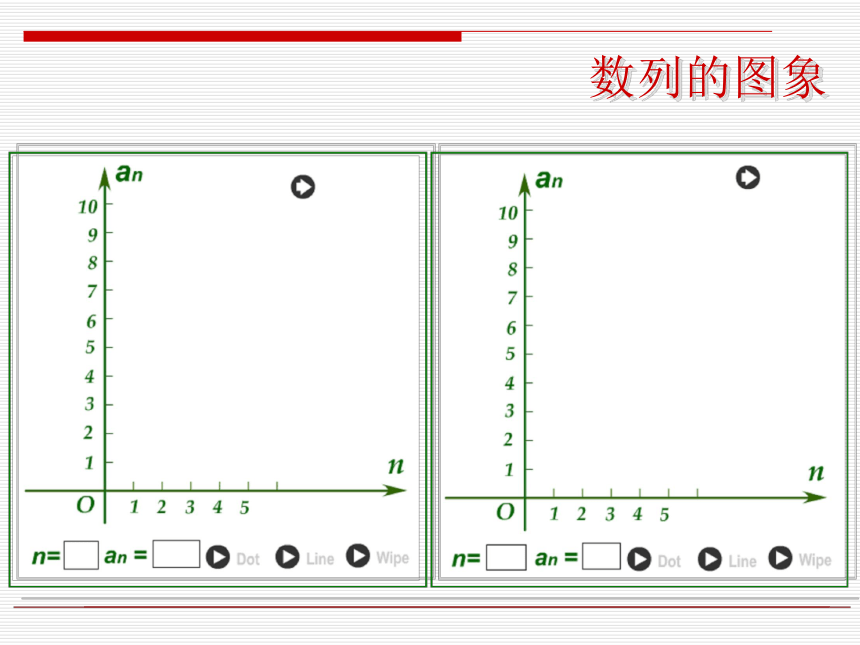
有何区别?区别1:数列中的项可以相同,但集合中的元素不能相同。区别2:数列中的项有一定的次序,而集合中的元素没有顺序。 区别3:数列中的项一定是数,而集合中的元素不一定是数。其中右下标n表示项的位置序号, 上面的数列又可简记为数列的一般形式可以写成: 对于数列中的每个序号n,都有唯一的一个数(项)an与之对应. 数列的项an与它对应的序号n能否用一个公式来表示呢? 从函数的观点看:数列可以看成以正整数集N*(或它的有限子集{1,2, …k})为定义域的函数an=f(n),当自变量按照从小到大的顺序依次取值时,所对应的一列函数值。反过来,对于函数y=f(x),如果f(i)(i=1,2,3, …)有意义 ,那么我们可以得到一个数列f(1),f(2),f(3), …,f(n) ,…(自变量)(函数值)如数列 2, 4, 6, …, 2n, …数列的通项公式已知数列{an}的通项公式为an=2n-1 ,用列表法写出这个数列的前5项,并作出图象.例1.解:数列的图象是一群孤立的点。数列的图象有何特点?y=2x-1问题1:数列的表示法:问题2:写出这个数列的第10项?问题3:2005是这个数列的项吗?2006呢? ∴ n=1003.5 N*
∴ 2006不是这个数列的项。
解:设2006是此数列的项,则 2n-1=2006例2. 写出数列的一个通项公式,使它的前4项分别是下列各数: (1) 1,4,9,16;找出项an与序号n的关系。关键是什么?an=n2练习:(2) -1, 1, -1, 1 an=(-1)n变题1:变题2:: 0, 2, 0, 2 an=1+(-1)n
注:给出数列的前几项,可以归纳
出不止一个通项公式。
注:并不是所有的数列都可以求出其
通项公式。
1,1,2,3,5,8,13,21,34….
这就是为以意大利著名数学家裴波那契命名的“裴波那契数列” .有趣的兔子数列裴波那契螺旋http://www.wxws.cn欢迎各位领导和同行指导数列的概念和简单表示, 26318446744073709551615陛下国库里的麦子不够啊!OK?某种细胞的分裂(1)传说中棋盘上麦粒数按放置的先后排成的一列数:
1,2,2 2,2 3,…,2 63(2)某种细胞分裂问题:1,2,4,8,16,…(6)从1984年到今年,我国体育健儿共参加了6次奥运会,获得的金牌数依次排成一列数: 15,5,16,16,28,32(3)π 精确到0.01,0.001,0.0001…的不足近似值排成一列数:3.14,3.141,3.1415,3.14159,3.141592…(5)某剧场有10排座位,第一排有20个座位,后一排都比前一排多2个,则各排的座位数依次为:20,22,24,26,…,38(4)人们在1740年发现了一颗彗星,并推算出它每隔83年出现一次,则从出现那次算起,这颗彗星出现的年份依次为1740,1823,1906,1989, …1、均是一列数,2、有一定次序.观察上面6个例子它们有什么共同特点?特点:(1)1,2,2 2,2 3,…,2 63(2)1,2,4,8,16,…(6)15,5,16,16,28,32(3)(5)20,22,24,26,28,…,38(4)1740,1823,1906,1989, …3.14,3.141,3.1415,3.14159,3.141592…★按一定次序排列的一列数叫数列.
定义★数列中的每一个数叫做这个数列的项.★项数有限的数列叫做有穷数列; 项数无限的数列叫做无穷数列.各项依次叫做这个数列的第1项(首项)、第2项、…、第n项…问题2: -1,1,-1,1是否是一数列?问题1: 数列:1,2,3,4,5
数列:5,4,3,2,1
它们是否是同一数列?
问题3: 数列中的项和集合中的 元素
有何区别?区别1:数列中的项可以相同,但集合中的元素不能相同。区别2:数列中的项有一定的次序,而集合中的元素没有顺序。 区别3:数列中的项一定是数,而集合中的元素不一定是数。其中右下标n表示项的位置序号, 上面的数列又可简记为数列的一般形式可以写成: 对于数列中的每个序号n,都有唯一的一个数(项)an与之对应. 数列的项an与它对应的序号n能否用一个公式来表示呢? 从函数的观点看:数列可以看成以正整数集N*(或它的有限子集{1,2, …k})为定义域的函数an=f(n),当自变量按照从小到大的顺序依次取值时,所对应的一列函数值。反过来,对于函数y=f(x),如果f(i)(i=1,2,3, …)有意义 ,那么我们可以得到一个数列f(1),f(2),f(3), …,f(n) ,…(自变量)(函数值)如数列 2, 4, 6, …, 2n, …数列的通项公式已知数列{an}的通项公式为an=2n-1 ,用列表法写出这个数列的前5项,并作出图象.例1.解:数列的图象是一群孤立的点。数列的图象有何特点?y=2x-1问题1:数列的表示法:问题2:写出这个数列的第10项?问题3:2005是这个数列的项吗?2006呢? ∴ n=1003.5 N*
∴ 2006不是这个数列的项。
解:设2006是此数列的项,则 2n-1=2006例2. 写出数列的一个通项公式,使它的前4项分别是下列各数: (1) 1,4,9,16;找出项an与序号n的关系。关键是什么?an=n2练习:(2) -1, 1, -1, 1 an=(-1)n变题1:变题2:: 0, 2, 0, 2 an=1+(-1)n
注:给出数列的前几项,可以归纳
出不止一个通项公式。
注:并不是所有的数列都可以求出其
通项公式。
