3.2 圆的对称性 课件(共28张PPT)
文档属性
| 名称 | 3.2 圆的对称性 课件(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-09 11:13:29 | ||
图片预览








文档简介
(共28张PPT)
3.2 圆的对称性
北师大版 九年级 下册
教学目标
教学目标:1.掌握圆的轴对称性和中心对称性.
2.掌握圆心角的概念.
3.掌握在同圆或等圆中,圆心角、弦、弧中有一个量相等就可
以推出其他的两个量对应相等,以及它们在解题中的应用.
教学重点:理解圆心角、弧、弦之间的关系.
教学难点:利用圆心角、弧、弦之间的关系进行计算.
观察与思考
观察图片,想一想,如何将一块蛋糕平均分成两块?四块?八块?分小组讨论一下.
新知讲解
合作学习
问题:什么是轴对称图形?
如果一个图形延着一条直线对折后两部分完全重合,那么这样的图形叫轴对称图形.
合作学习
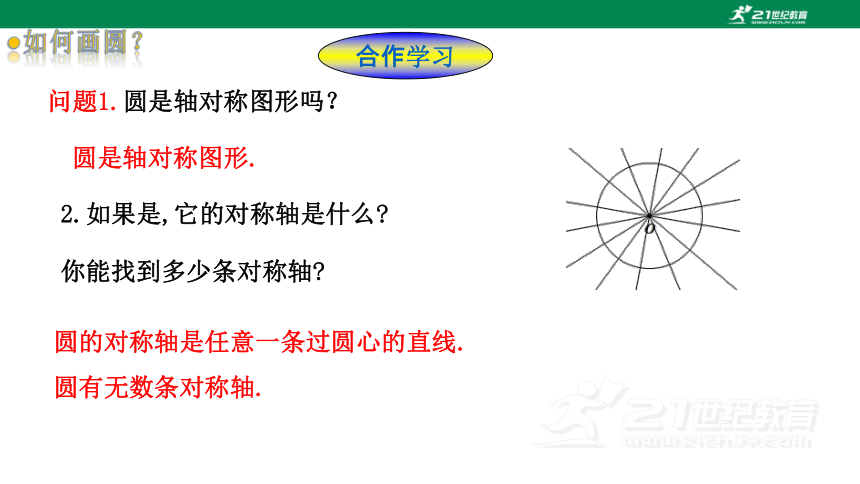
如何画圆?
问题1.圆是轴对称图形吗?
圆是轴对称图形.
圆的对称轴是任意一条过圆心的直线.
圆有无数条对称轴.
2.如果是,它的对称轴是什么
你能找到多少条对称轴
问题2 你是怎么得出结论的?
用折叠的方法
圆的对称性1:
圆是轴对称图形,其对称轴是直径所在的直线.
问题3:1.将圆绕圆心旋转180°后,得到的图形与原图形重合吗?由此你得到什么结论呢?
·
它具有旋转不变性.
一个圆绕着它的圆心旋转任意一个角度,都能与原来的图形重合.
圆具有旋转对称性——一个圆绕着它的圆心旋转任意一个角度之后,都能与原来的图形重合.
特别的,圆是中心对称图形,对称中心为圆心.
圆心角与所对的弧、弦之间的关系
探究
圆心角的定义:顶点在圆心的角叫做圆心角.
圆心角的判断方法:观察顶点是否在圆心.
A
O·
B
C
问题一 找出⊙O中的圆心角?
问题二:∠ABC是不是圆心角?并说明原因?
∠AOC、 ∠BOC
不是,顶点不在圆心.
如图,将圆心角∠AOB绕圆心O旋转到∠A1OB1的位置,你能发现哪些等量关系?为什么?
·
O
A
B
A1
B1
AB=A1B1 AB=A1B1
⌒
⌒
∵∠AOB=∠A1OB1
∴射线OB与OB1重合
而同圆的半径相等,OA=OA1,OB=OB1
∴点A与A1重合,B与B1重合.
因此AB与A1B1重合, 弦AB与A1B1重合,
即AB=A1B1 AB=A1B1
⌒
⌒
⌒
⌒
探索与思考
AB=A'B'
AB = A'B'
⌒
⌒
如图,在等圆中,如果∠AOB=∠A'O'B',你发现的等量关系是否依然成立?为什么?
由∠AOB=∠A'O'B'得到
B
A
● O
A'
B'
● O'
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
在同圆或等圆中,两条弧相等,则他们所对应的其余各组量有什么关系?
·
O
A
B
B1
A1
在同圆或等圆中,相等的弧所对的圆心角相等,所对的弦相等
将弧AB绕圆心O旋转,使弧AB与弧A1B1重合
∴点A与A1重合,B与B1重合
∴射线OB与OB1重合,射线OA与OA1重合
∴∠AOB=∠A1OB1
而同圆的半径相等OA=OA1,OB=OB1
∴AB=A1B1
⌒
⌒
⌒
提炼概念
在同圆或等圆中,两条弦相等,则他们所对应的其余各组量有什么关系?
·
O
A
B
B1
A1
在同圆或等圆中,相等的弦所对的圆心角相等,
所对优弧和劣弧分别相等
⌒
⌒
在△AOB和△A1OB1
OA=OA1
OB=OB1
AB=A1B1
∴△AOB≌△A1OB1
∴∠AOB=∠A1OB1
∴AB=A1B1
∴AA1B=A1AB1
⌒
⌒
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对的其余各组量都分别相等.
·
O
A
B
B1
A1
【问题】“同圆或等圆”的条件能少吗?
不能少,理由:如图下图,已知∠COD= ∠AOB
但是线段CD不等于线段AB ,弧CD也不等于弧AB.
练一练
已知:如图,AB,CD是⊙O的两条弦,
根据这节课所学的结论填空:
⌒
⌒
(2)如果AB=CD,那么 , ;
(3)如果AB=CD,那么 , 。
(1) 如果∠AOB=∠COD,那么 , ;
AB=CD
∠AOB=∠COD AB=CD
∠AOB=∠COD
典例精讲
如图, AB,DE是⊙O的直径,C是⊙O上的一点,且
. BE与CE的大小有什么关系?为什么?
例
解:
BE=CE. 理由是
∵ ∠AOD=∠BOE,
∴
又∵
∴
∴ BE=CE.
归纳概念
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
弧、弦与圆心角关系定理的推论
在一个圆中,如果圆心角相等,那么它们所对的弧_____,所对的弦_____.
在一个圆中,如果弧相等,那么所对的圆心角_____,所对的弦______.
在一个圆中,如果弦相等,那么所对的圆心角____,圆心角所对的弧____.
等圆中也同样.
相等
相等
相等
相等
相等
相等
课堂练习
1.下列说法中,不正确的是( )
A.过圆心的弦是圆的直径 B.等弧的长度一定相等
C.周长相等的两个圆是等圆 D.直径是弦,半圆不是弧
【详解】A.直径是通过圆心且两个端点都在圆上的线段,故正确
B.能重合的弧叫等弧,长度相等,故正确
C.周长相等的圆其半径也相等,为等圆,故正确
D.直径是弦,半圆是弧,故错误
故选:D
2.如图,已知A,B,C,D是⊙O上的点,∠1=∠2,则下列结论中正确的有( ) ①AB=CD;②BD=AC;③AC=BD;④∠BOD=∠AOC.
A.1个 B.2个
C.3个 D.4个
D
⌒
⌒
⌒
⌒
3.如图.A,B,C、D是圆O上的四点,AB=DC,△ABC与△DCB全等吗?为什么?
解∶△ABC≌△DCB.理由是∶
∵ AB=CD
∴ AB=CD
⌒
⌒
∴CA=BD
⌒
⌒
∴AC=BD
∵ AC=BD
AB=CD
BC=CB
∴△ABC≌△DCB
4.如图,⊙O中,弦AB与CD相交于点E,AB=CD,连接AD、BC.求证:
(1)AD=BC
(2)AE=CE.
【详解】(1)证明:∵AB=CD,
∴弧AB=弧CD,
∴弧AB-弧AC=弧CD-弧AC,
∴弧AD=弧BC,
∴AD=BC;
(2)∵∠ADE=∠CBE,∠AED=∠CEB,AD=BC
∴△ADE≌△CBE(AAS),
∴AE=EC.
5.如图.AB是圆O的直径,OD//AC. CD与BD的大小有什么关系 为什么
⌒
⌒
解∶CD=BD.理由是∶
⌒
⌒
∵OD//AC
∴∠ACO=∠COD
∠CAO=∠DOB
又∵OC=OA
∴∠ACO=∠CAO
∴∠COD=∠DOB
∴CD=BD
⌒
⌒
课堂总结
1、圆的对称性
圆的轴对称性(圆是轴对称图形)
圆的中心对称性(圆是中心对称图形)
圆心角、弧、弦之间的关系
2、证明圆弧相等:(1)定义
(2)圆心角、弧、弦之间的关系
3、证明线段相等:(1)利用原来的证“角相等,三角形全等”等方法
(2)圆心角、弧、弦之间的关系
对称轴是过圆心的直线
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
3.2 圆的对称性
北师大版 九年级 下册
教学目标
教学目标:1.掌握圆的轴对称性和中心对称性.
2.掌握圆心角的概念.
3.掌握在同圆或等圆中,圆心角、弦、弧中有一个量相等就可
以推出其他的两个量对应相等,以及它们在解题中的应用.
教学重点:理解圆心角、弧、弦之间的关系.
教学难点:利用圆心角、弧、弦之间的关系进行计算.
观察与思考
观察图片,想一想,如何将一块蛋糕平均分成两块?四块?八块?分小组讨论一下.
新知讲解
合作学习
问题:什么是轴对称图形?
如果一个图形延着一条直线对折后两部分完全重合,那么这样的图形叫轴对称图形.
合作学习
如何画圆?
问题1.圆是轴对称图形吗?
圆是轴对称图形.
圆的对称轴是任意一条过圆心的直线.
圆有无数条对称轴.
2.如果是,它的对称轴是什么
你能找到多少条对称轴
问题2 你是怎么得出结论的?
用折叠的方法
圆的对称性1:
圆是轴对称图形,其对称轴是直径所在的直线.
问题3:1.将圆绕圆心旋转180°后,得到的图形与原图形重合吗?由此你得到什么结论呢?
·
它具有旋转不变性.
一个圆绕着它的圆心旋转任意一个角度,都能与原来的图形重合.
圆具有旋转对称性——一个圆绕着它的圆心旋转任意一个角度之后,都能与原来的图形重合.
特别的,圆是中心对称图形,对称中心为圆心.
圆心角与所对的弧、弦之间的关系
探究
圆心角的定义:顶点在圆心的角叫做圆心角.
圆心角的判断方法:观察顶点是否在圆心.
A
O·
B
C
问题一 找出⊙O中的圆心角?
问题二:∠ABC是不是圆心角?并说明原因?
∠AOC、 ∠BOC
不是,顶点不在圆心.
如图,将圆心角∠AOB绕圆心O旋转到∠A1OB1的位置,你能发现哪些等量关系?为什么?
·
O
A
B
A1
B1
AB=A1B1 AB=A1B1
⌒
⌒
∵∠AOB=∠A1OB1
∴射线OB与OB1重合
而同圆的半径相等,OA=OA1,OB=OB1
∴点A与A1重合,B与B1重合.
因此AB与A1B1重合, 弦AB与A1B1重合,
即AB=A1B1 AB=A1B1
⌒
⌒
⌒
⌒
探索与思考
AB=A'B'
AB = A'B'
⌒
⌒
如图,在等圆中,如果∠AOB=∠A'O'B',你发现的等量关系是否依然成立?为什么?
由∠AOB=∠A'O'B'得到
B
A
● O
A'
B'
● O'
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
在同圆或等圆中,两条弧相等,则他们所对应的其余各组量有什么关系?
·
O
A
B
B1
A1
在同圆或等圆中,相等的弧所对的圆心角相等,所对的弦相等
将弧AB绕圆心O旋转,使弧AB与弧A1B1重合
∴点A与A1重合,B与B1重合
∴射线OB与OB1重合,射线OA与OA1重合
∴∠AOB=∠A1OB1
而同圆的半径相等OA=OA1,OB=OB1
∴AB=A1B1
⌒
⌒
⌒
提炼概念
在同圆或等圆中,两条弦相等,则他们所对应的其余各组量有什么关系?
·
O
A
B
B1
A1
在同圆或等圆中,相等的弦所对的圆心角相等,
所对优弧和劣弧分别相等
⌒
⌒
在△AOB和△A1OB1
OA=OA1
OB=OB1
AB=A1B1
∴△AOB≌△A1OB1
∴∠AOB=∠A1OB1
∴AB=A1B1
∴AA1B=A1AB1
⌒
⌒
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对的其余各组量都分别相等.
·
O
A
B
B1
A1
【问题】“同圆或等圆”的条件能少吗?
不能少,理由:如图下图,已知∠COD= ∠AOB
但是线段CD不等于线段AB ,弧CD也不等于弧AB.
练一练
已知:如图,AB,CD是⊙O的两条弦,
根据这节课所学的结论填空:
⌒
⌒
(2)如果AB=CD,那么 , ;
(3)如果AB=CD,那么 , 。
(1) 如果∠AOB=∠COD,那么 , ;
AB=CD
∠AOB=∠COD AB=CD
∠AOB=∠COD
典例精讲
如图, AB,DE是⊙O的直径,C是⊙O上的一点,且
. BE与CE的大小有什么关系?为什么?
例
解:
BE=CE. 理由是
∵ ∠AOD=∠BOE,
∴
又∵
∴
∴ BE=CE.
归纳概念
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
弧、弦与圆心角关系定理的推论
在一个圆中,如果圆心角相等,那么它们所对的弧_____,所对的弦_____.
在一个圆中,如果弧相等,那么所对的圆心角_____,所对的弦______.
在一个圆中,如果弦相等,那么所对的圆心角____,圆心角所对的弧____.
等圆中也同样.
相等
相等
相等
相等
相等
相等
课堂练习
1.下列说法中,不正确的是( )
A.过圆心的弦是圆的直径 B.等弧的长度一定相等
C.周长相等的两个圆是等圆 D.直径是弦,半圆不是弧
【详解】A.直径是通过圆心且两个端点都在圆上的线段,故正确
B.能重合的弧叫等弧,长度相等,故正确
C.周长相等的圆其半径也相等,为等圆,故正确
D.直径是弦,半圆是弧,故错误
故选:D
2.如图,已知A,B,C,D是⊙O上的点,∠1=∠2,则下列结论中正确的有( ) ①AB=CD;②BD=AC;③AC=BD;④∠BOD=∠AOC.
A.1个 B.2个
C.3个 D.4个
D
⌒
⌒
⌒
⌒
3.如图.A,B,C、D是圆O上的四点,AB=DC,△ABC与△DCB全等吗?为什么?
解∶△ABC≌△DCB.理由是∶
∵ AB=CD
∴ AB=CD
⌒
⌒
∴CA=BD
⌒
⌒
∴AC=BD
∵ AC=BD
AB=CD
BC=CB
∴△ABC≌△DCB
4.如图,⊙O中,弦AB与CD相交于点E,AB=CD,连接AD、BC.求证:
(1)AD=BC
(2)AE=CE.
【详解】(1)证明:∵AB=CD,
∴弧AB=弧CD,
∴弧AB-弧AC=弧CD-弧AC,
∴弧AD=弧BC,
∴AD=BC;
(2)∵∠ADE=∠CBE,∠AED=∠CEB,AD=BC
∴△ADE≌△CBE(AAS),
∴AE=EC.
5.如图.AB是圆O的直径,OD//AC. CD与BD的大小有什么关系 为什么
⌒
⌒
解∶CD=BD.理由是∶
⌒
⌒
∵OD//AC
∴∠ACO=∠COD
∠CAO=∠DOB
又∵OC=OA
∴∠ACO=∠CAO
∴∠COD=∠DOB
∴CD=BD
⌒
⌒
课堂总结
1、圆的对称性
圆的轴对称性(圆是轴对称图形)
圆的中心对称性(圆是中心对称图形)
圆心角、弧、弦之间的关系
2、证明圆弧相等:(1)定义
(2)圆心角、弧、弦之间的关系
3、证明线段相等:(1)利用原来的证“角相等,三角形全等”等方法
(2)圆心角、弧、弦之间的关系
对称轴是过圆心的直线
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
