立体几何全部复习课件[上下学期通用]
图片预览








文档简介
课件406张PPT。立体几何复习课件
平行问题垂直问题角度问题距离问题柱锥问题体积面积问题多面体与球的问题生活问题和翻折问题综合问题立几概念和方法动态的立体几何正方体的截面问题三棱柱的体积分割平行问题返回直线和平面的位置关系直线和平面的平行关系平面和平面的平行关系返回直线在平面内直线和平面相交直线和平面平行线面位置关系有无数个公共点有且仅有一个公共点没有公共点返回平行于同一平面的二直线的位置关系是 ( )(A) 一定平行(B) 平行或相交(C) 相交(D) 平行,相交,异面D返回(1)点A是平面?外的一点,过A和平面?平行的直线有 条。α无数返回(2)点A是直线l 外的一点,过A和直线l 平行的平面有 个。无数返回(3)过两条平行线中的一条和另一条平行的平面有 个。无数返回(4)过两条异面直线中的一条和另一条平行的平面有 个。且仅有一返回(5)如果l1 // l2 , l1 平行于平面?,则l2 平面?l1?? 或 //返回(6)如果两直线a,b相交,a平行于平面?,则b与平面?的位置关系是 。a?相交或平行返回过直线L外两点,作与直线L平行的平面,这样的平面( )(A) 有无数个(C) 只能作出一个(B) 不能作出(D) 以上都有可能情况一返回(A) 有无数个(C) 只能作出一个(B) 不能作出(D) 以上都有可能过直线L外两点,作与直线L平行的平面,这样的平面( )情况二返回过直线L外两点,作与直线L平行的平面,这样的平面( )(A) 有无数个(C) 只能作出一个(B) 不能作出(D) 以上都有可能D情况三返回例: 有以下四个命题:
① 若一条直线与另一条直线平行,则它就与经过另一条直线的平面平行;
② 若一条直线垂直于一个平面的一条垂线,则此直线平行于这个平面;
③ 若一条直线和一个平面内的两条直线都垂直,则此直线必垂直于这个平面;
④ 平面内两条平行直线,若其中一条直线与一个平面平行,则另一条直线也与这个平面平行. 其中正确命题的个数是( ).
A.0 B.1 C.2 D.3返回解:① 不正确,若一条直线与另一条直线平行,则这条直线可能与经过另一条直线的平面平行,也可能在平面内;
② 不正确,与①相仿,若一条直线垂直于一个平面的一条垂线,则此直线可能平行于这个平面,也可能在平面内;返回 ③ 不正确,若一条直线和一个平面内的两条直线都垂直,如果在平面内的两条直线平行,则无法判断直线是否垂直于这个平面;
④ 不正确,与①②相仿,该直线仍有可能在平面内。
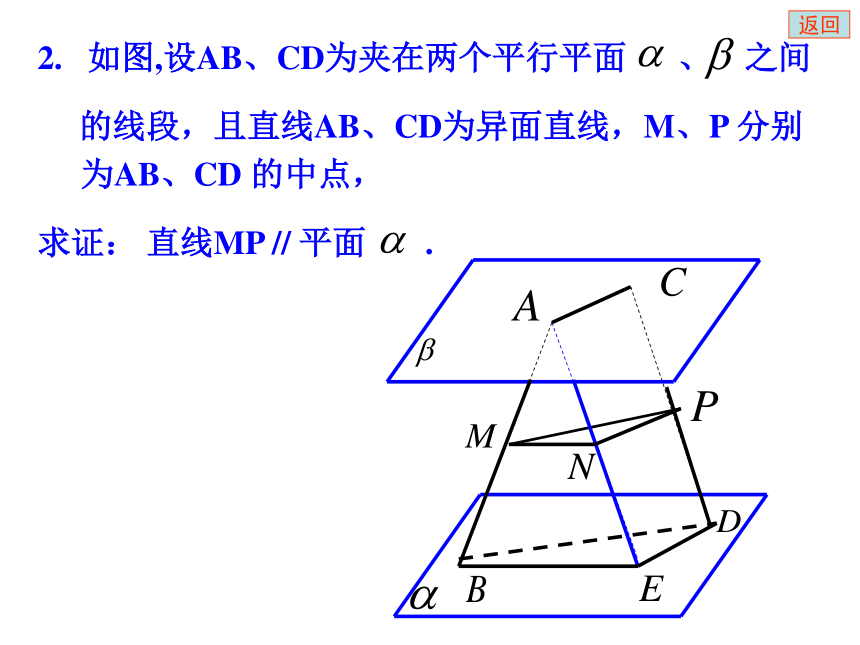
所以四个命题都是错误的,选A。返回线面平行的判定(1)定义——直线与平面没有公共点(2)定理——如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。返回线面平行判定定理——如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。已知:a??? b??? a//b求证:a//?ab?(1) a,b确定平面?,???=b(2) 假设a与?不平行则a与?有公共点P则P? ???=b(3) 这与已知a//b矛盾(4) ∴a // ??返回 如图,空间四面体P-ABC,M,N分别是面PCA和面PBC的重心,求证:MN//面BCAP∵MN// EF∴ MN //面BCA线线平行线面平行返回如图,两个全等的正方形ABCD和ABEF所在平面交于AB,M.N分别是对角线上的点,AM=FN。求证:MN//面BCE。ABCDEFMN∵MN // GH∴ MN //面BCE线线平行线面平行返回ABCDEFMN∵△AFN∽ △BNH∴ AN/NH=FN/BN∴ AN/NH=AM/MC∴ MN//CH∴ MN //面BCE如图,两个全等的正方形ABCD和ABEF所在平面交于AB, M.N分别是对角线上的点,AM=FN,求证:MN//面BCE。返回 在正方体AC1中,E为DD1的中点,求证:DB1//面A1C1EE∵DB1 // EF∴ DB1 //面A1C1E线线平行线面平行返回在正方体AC1中,O为平面ADD1A1的中心,求证:CO // 面A1C1BB1O返回(1)如果一条直线与一个平面平行,则这条直线与这个平面无公共点(2)如果一条直线与一个平面平行,则这条直线与这个平面内的直线成异面直线或平行直线(3)如果一条直线与一个平面平行,经过这条直线的平面和这个平面相交,则这条直线与交线平行。返回已知:a//?,a??, ? ? ?=b求证:a//b? ? ?=bb ? ?a //?a ? b=?a//b返回如果平面外的两条平行线中的一条与这个平面平行,则另一条直线与这个平面也平行abc返回如果一条直线和两个相交平面都平行,则这条直线与它们的交线平行a??l已知:a // ?, a// ? ,? ? ?=l求证:a // l返回abABOMNP如图,a,b是异面直线,O为AB的中点,过点O作平面?与两异面直线a,b都平行MN交平面于点P,求证:MP=PN?返回一、两个平面平行的判定方法1、两个平面没有公共点2、一个平面内有两条相交直线都平行于另一个平面3、都垂直于同一条直线的两个平面两个平面平行返回二、两个平面平行的性质4、一直线垂直于两个平行平面中的一个,则它也垂直于另一个平面2、其中一个平面内的直线平行于另一个平面3、两个平行平面同时和第三个平面相交,它们的交线平行两个平面平行5、夹在两个平行平面间的平行线段相等1、两个平面没有公共点返回判断下列命题是否正确?1、平行于同一直线的两平面平行2、垂直于同一直线的两平面平行3、与同一直线成等角的两平面平行返回4.垂直于同一平面的两平面平行5.若α∥β,则平面α内任一直线a ∥β返回2. 如图,设AB、CD为夹在两个平行平面 、 之间
的线段,且直线AB、CD为异面直线,M、P 分别为AB、CD 的中点,
求证: 直线MP // 平面 .返回例:如图,在正方体ABCD-A1B1C1D1 中,求证:面AB1D1∥面BDC1证明:B1D1∩AB1=B1面AB1D1∥
面BDC1线∥线线∥面面∥面返回证法2:A1C⊥BDBD∩BC1=BA1C⊥面BDC1面AB1D1
∥面BDC1返回变形1:如图,在正方体ABCD-A1B1C1D1中,E,F,G分别为A1D1,A1B1,A1A的中点,求证:面EFG∥面BDC1变形2:若O为BD上的点
求证:OC1 ∥面EFG
O面∥面 由上知面EFG∥面BDC1线∥面OC1 ∥面EFG证明:返回变形3:如图,在正方体ABCD-A1B1C1D1 中,E,F,M,N分别为A1B1,A1D1, B1C1, C1D1 的中点求证:面AEF∥面BDMN返回小结:线
平行
线 线
平行
面 面
平行
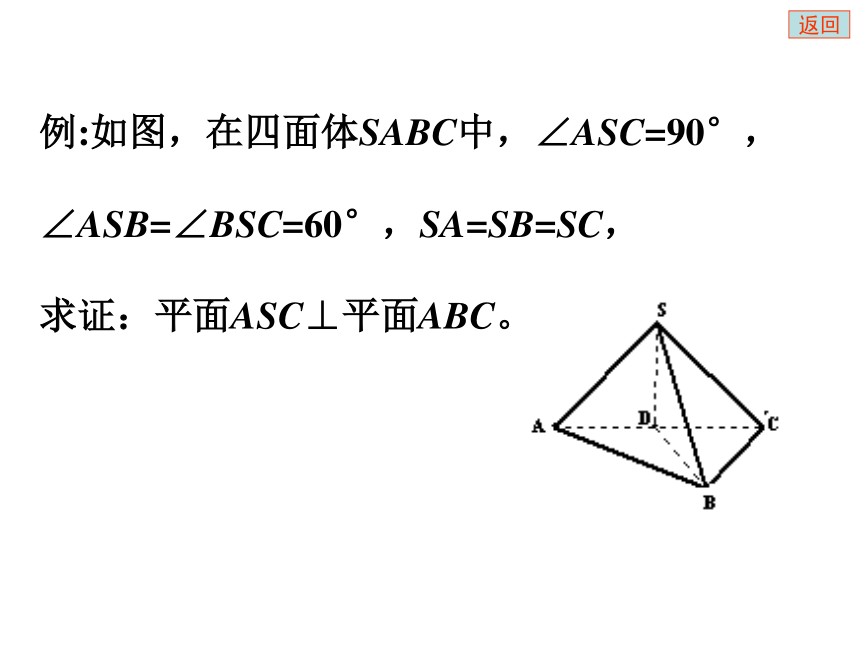
面线面平行判定线面平行性质面面平行判定面面平行性质三种平行关系的转化返回 已知:四面体A-BCD,E,F,G分别为AB,AC,AD的中点.求证:面EFG∥面BCD练习返回垂直问题线面垂直的判定方法(1)定义——如果一条直线和一个平面内的任意一条直线都垂直,则直线与平面垂直。(2)判定定理1——如果两条平行线中的一条垂直于一个平面,则另一条也垂直于这个平面。(3)判定定理2——如果一条直线和一个平面内的两条相交直线都垂直,则直线与平面垂直。返回线面垂直的性质(1)定义——如果一条直线和一个平面垂直则这条直线垂直于平面内的任意一条直线(2)性质定理——如果两条直线同垂直于一个平面,则这两条直线平行。返回填空(1)l ?? , m?? ? l____m(2) n??, m?? , m与n_____, l ?m, l ?n, ? l ?? (3)l ?? , m ?? , ? l____m(4)l //m , l ?? , ? m____ ?相交?//?返回PABC?如图,AB是圆O的直径,C是异于A,B的圆周上的任意一点,PA垂直于圆O所在的平面(1)BC⊥面PAC返回PABC?2)若AH⊥PC,则AH⊥面PBC如图,AB是圆O的直径,C是异于A,B的圆周上的任意一点,PA垂直于圆O所在的平面返回O在正方体AC1中,O为下底面的中心,求证:AC⊥面D1B1BD返回OH在正方体AC1中,O为下底面的中心,B1H ⊥D1O,求证:B1H⊥面D1AC返回已知: l // ? ,m? ?求证: l ? m m?返回返回如果一个平面经过另一个平面的一条垂线,则这两个平面互相垂直返回如图,C为以AB为直径的圆周上一点, PA⊥面ABC,找出图中互相垂直的平面。∵PA⊥面ABC∴面PAC⊥面ABC∴面PAB⊥面ABC∵BC⊥面PAC∴面PBC⊥面PAC返回如果两个平面垂直,则在一个平面内垂直于它们的交线的直线垂直于另一个平面返回求证:如果一个平面与另一个平面的垂线平行,则这两个平面互相垂直??返回求证:如果两个相交平面都与另一个平面垂直,则这两个平面的交线 l 垂直于另一个平面???l返回求证:如果两个相交平面都与另一个平面垂直,则这两个平面的交线 l 垂直于另一个平面???l返回四面体ABCD中,面ADC⊥面BCD,面ABD ⊥面BCD,设DE是BC边上的高, 求证: 平面ADE ⊥面ABC 面ADC⊥面BCD面ABD ⊥面BCDAD ⊥面BCDAD ⊥BCDE ⊥BCBC ⊥面ADE面ABC ⊥面ADE①②③④返回⊿ABC是直角三角形, ∠ACB=90°,P为平面外一点,且PA=PB=PC . 求证: 平面PAB ⊥面ABC 返回课堂练习课堂练习空间四面体ABCD中,若AB=BC,AD=CD,E为AC的中点,则有( )(A) 平面ABD ⊥面BCD(B) 平面BCD ⊥面ABC(C) 平面ACD ⊥面ABC(D) 平面ACD ⊥面BDE返回如图,ABCD是正方形,PA ⊥面ABCD,连接PB,PC,PD,AC,BD,问图中有几对互相垂直的平面?面PAC⊥面ABCD面PAB⊥面ABCD面PAD⊥面ABCD面PAD⊥面PAB面PAD⊥面PCD面PBC⊥面PAB面PBD⊥面PAC返回如图,三棱锥P-ABC中,PB⊥底面ABC,∠ACB= 90°,PB=BC=CA,E为PC中点,返回如图,四棱锥P-ABCD的底面是菱形,PA⊥底面ABCD,∠BAD= 120°,E为PC上任意一点,返回例:如图,在四面体SABC中,∠ASC=90°,∠ASB=∠BSC=60°,SA=SB=SC,
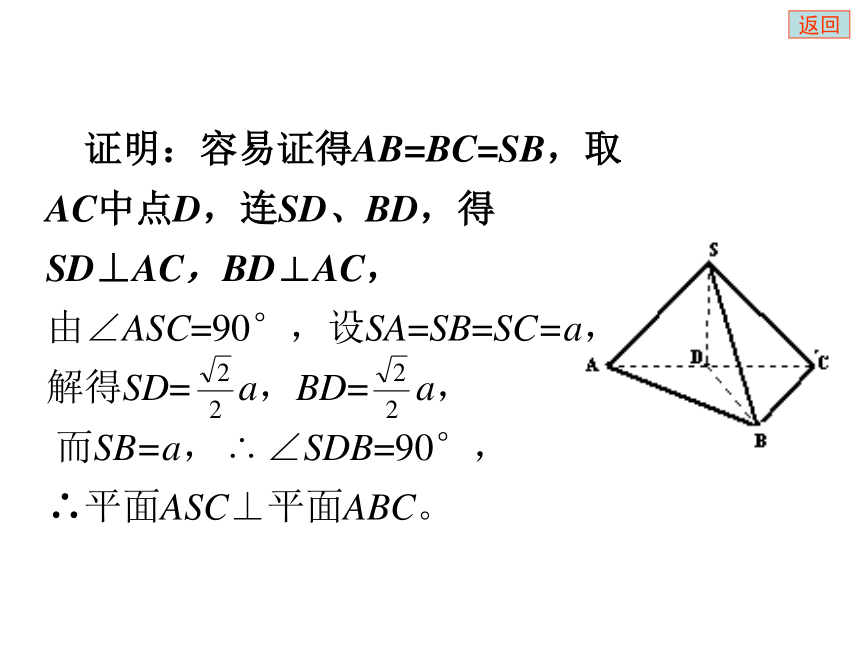
求证:平面ASC⊥平面ABC。返回 证明:容易证得AB=BC=SB,取AC中点D,连SD、BD,得SD⊥AC,BD⊥AC,
由∠ASC=90°,设SA=SB=SC=a,
解得SD= a,BD= a,
而SB=a, ∴ ∠SDB=90°,
∴平面ASC⊥平面ABC。返回角度问题一、概念直线a、b是异面直线,经过空间任意一点o,作直线a’、b’,并使a’//a,b’//b,我们把直线a’和b’所成的锐角(或直角)叫做异面直线a和b所成的角。返回aαbO是空间中的任意一点 点o常取在两条异面直线中的一条上θooooo返回一、概念直线a、b是异面直线,经过空间任意一点o,作直线a’、b’,并使a’//a,b’//b,我们把直线a’和b’所成的锐角(或直角)叫做异面直线a和b所成的角。返回θαBA返回一、概念直线a、b是异面直线,经过空间任意一点o,作直线a’、b’,并使a’//a,b’//b,我们把直线a’和b’所成的锐角(或直角)叫做异面直线a和b所成的角。从一条直线出发的两个半平面所组成的图形叫做二面角。以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角。返回ABO返回一、概念直线a、b是异面直线,经过空间任意一点o,作直线a’、b’,并使a’//a,b’//b,我们把直线a’和b’所成的锐角(或直角)叫做异面直线a和b所成的角。从一条直线出发的两个半平面所组成的图形叫做二面角。以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角。AαβLBO返回二、数学思想、方法、步骤: 解决空间角的问题涉及的数学思想主要是化归与转化,即把空间的角转化为平面的角,进而转化为三角形的内角,然后通过解三角形求得。2.方法:3.步骤:b.求直线与平面所成的角:a.求异面直线所成的角:c.求二面角的大小:①作(找)② 证③ 点④ 算1.数学思想:返回在正方体AC1中,求异面直线A1B和B1C所成的角?A1B和B1C所成的角为60°和A1B成角为60°的面对角线共有 条。返回在正方体AC1中,求异面直线D1B和B1C所成的角?ABDCA1B1D1C1返回在正方体AC1中,M,N分别是A1A和B1B的中点,求异面直线CM和D1N所成的角?MN返回PABCMN空间四边形P-ABC中,M,N分别是PB,AC的中点,PA=BC=4,MN=3,求PA与BC所成的角?返回1. 在正方体AC1中,E、G分别是AA1和
CC1的中点, F在AB上,且C1E⊥EF,
则EF与GD所成的角的大小为( )
(A) 30° (B) 45° (C) 60°(D) 90°DM EB1是EC1在平面AB1
内的射影EB1 ⊥EF
DG∥AM∥EB1
EF ⊥DG返回已知:两异面直线a,b所成的角是50 °,P为
空间中一定点,则过点P且与a,b都成30°角的
直线有 条。abPO2返回A1ABB1CDC1D1FE解:如图,取AB的中点G ,O(证)(点)(算)(作)例1:如图,在正方体ABCD-A1B1C1D1中,E、F分别是BB1 、CD中点。求AE与D1F所成的角。返回例2、长方体ABCD-A' B'C' D'中, AB=BC=4, AA' =6, E、F分别为BB' 、CC'的中点, 求AE、BF所成角的余弦值.返回例3:长方体ABCD-A1B1C1D1,AB=AA1=2 cm, AD=1cm,求异面直线A1C1与BD1所成角的余弦值。返回取BB1的中点M,连O1M,则O1M??D1B,如图,连B1D1与A1C1 交于O1,于是?A1O1M就是异面直线A1C1与BD1所成的角(或其补角)O1M解:为什么?返回解法二:方法归纳:补形法把空间图形补成熟悉的或完整的几何体,如正方体、长方体等,其目的在于易于发现两条异面直线的关系。 返回解法二:方法归纳:补形法把空间图形补成熟悉的或完整的几何体,如正方体、长方体等,其目的在于易于发现两条异面直线的关系。 在?A1C1E中,由余弦定理得?A1C1与BD1所成角的余弦值为 如图,补一个与原长方体全等的并与原长方体有公共面连结A1E,C1E,则?A1C1E为A1C1与BD1所成的角(或补角),BC1的长方体B1F,返回例: 如图,在正方体 ABCD-A1B1C1D1中,异面直线AC与BC1所成角的大小是( ).
A.30° B.45° C.60° D.90°返回例: 如图,正三棱锥S-A BC的侧棱与底面边长相等,如果E、F分别为SC、 A B的中点,那么异面直线EF与SA所成角等于( ) A.90° B.60° C.45° D.30°返回解:取AC的中点G,连接EG、FG,
∵ EG//SA,∴ ∠GEF是异面直线EF与SA所成角,又FG//BC,SA⊥BC,
∴ ∠EGF=90°,
△EGF是直角三角形,又EG=SA,FG=BC,
∴ EG=FG,△EGF是等腰直角三角形,
∴ ∠GEF=45°,选C.返回
正方体ABCD- A1B1C1D1中,AC、BD交于O,则OB1与A1C1所成的角的度数为练习1900返回在正四面体S-ABC中,SA⊥BC, E, F分别为SC、AB 的中点,那么异面直线EF 与SA 所成的角等于( )CD(A)300 (B)450 (C)600 (D)900练习2B返回例:已知正方体的棱长为 a , M 为 AB 的中点, N 为 BB1的中点,求 A1M 与 C1 N 所成角的余弦值。解:EG如图,取AB的中点E, 连BE, 有BE∥ A1M 取CC1的中点G,连BG. 有BG∥ C1N 则∠EBG即为所求角。BG=BE= a, F C1 = a由余弦定理,cos∠EBG=2/5F取EB1的中点F,连NF,有BE∥NF则∠FNC为所求角。想一想:还有其它定角的方法吗?在△EBG中返回定角一般方法有:(1)平移法(常用方法)小结:1、求异面直线所成的角是把空间角转化为平面 角,体现了化归的数学思想。2、用余弦定理求异面直线所成角时,要注意角的 范围: (1) 当 cosθ > 0 时,所成角为 θ(2) 当 cosθ < 0 时,所成角为π- θ(3) 当 cosθ = 0 时,所成角为 3、当异面直线垂直时,还可应用线面垂直的有 关知识解决。90o(2)补形法化归的一般步骤是:定角求角返回说明:异面直线所成角的范围是(0, ],在把异面直线所成的角平移转化为平面三角形中的角,常用余弦定理求其大小,当余弦值为负值时,其对应角为钝角,这不符合两条异面直线所成角的定义,故其补角为所求的角,这一点要注意。 返回斜线与平面所成的角平面的一条斜线和它在这个平面内的射影所成的锐角返回若斜线段AB的长度是它在平面?内的射影长的2倍,则AB与?所成的角为 。60°返回最小角原理C斜线与平面所成的角,是这条斜线和这个平面内的直线所成的一切角中最小的角。返回若直线 l1与平面所成的角为60 ° ,则这条直线与平面内的直线所成的一切角中最小的角 ,最大的角为 。90°60°Ol1返回若直线 l1与平面所成的角为30 ° ,直线 l2 与 l1 所成的角为60 °,求直线 l2与平面所成的角 的范围?l1返回如图,直线OA与平面?所成的角为?,平面内一条直线OC与OA的射影OB所成的角为,设∠AOC为?2求证:cos?2= cos ?1 ×cos ?返回求直线与平面所成的角时,应注意的问题:(1)先判断直线与平面的位置关系(2)当直线与平面斜交时,常采用以下步骤:①作出或找出斜线上的点到平面的垂线②作出或找出斜线在平面上的射影③求出斜线段,射影,垂线段的长度④解此直角三角形,求出所成角的相应函数值返回例题:如图,在正方体ABCD-A1B1C1D1中,求A1B与平面A1B1CD所成的角O返回SACBOFE如图,?ACB=90?,S为平面ABC外一点, ?SCA= ?SCB= 60?,求SC与平面ACB所成的角.返回SACBOFE如图,SA,SB,SC是三条射线,?BSC=60?,SA上一点P到平面BSC的距离是3, P到SB,SC的距离是5,求SA与平面BSC所成的角P返回ABCDFEADFD’A’CA1BE正方形ABCD边长为3,AE=2BE,CF=2DF,沿EF将直角梯形AEFD折起,使点A’的射影点G落在边BC上,求A’E与平面ABCD所成的角?返回如图,在正方体ABCD-A1B1C1D1中,O为下底面AC的中心,求A1O与平面BB1D1D所成的角.OO`返回正四面体P—ABC中,求侧棱PA与
底面ABC所成的角PABCD返回从一条直线出发的两个半平面所形成的图形叫做二面角这条直线叫做二面角的棱从一条直线出发的两个半平面所形成的图形叫做二面角这条直线叫做二面角的棱返回以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角返回基础题例题1.下列命题中:
①两个相交平面组成的图形叫做二面角;
②异面直线a、b分别和一个二面角的两个面垂直,则a、b组成的角与这个二面角的平面角相等或互补;
③二面角的平面角是从棱上一点出发,分别在两个面内作射线所成角的最小角;
④正四面体相邻两个面所成的二面角的平面角是锐角.
其中,正确命题的序号是______________.②、④返回2.如图,正方体ABCD—A1B1C1D1中,二面角B1-AA1-C1的大小为_____,二面角B-AA1-D的大小为______,二面角C1-BD-C的正切值是_______.45°90°基础题例题返回3. 在二面角α-l-β的一个平面α内有一条直线AB,它 与棱 l 所成的角为45°,与平面β所成的角为30°,则 这个二面角的大小是________________.45°或135°基础题例题返回B4. 在二面角α-a-β内,过a作一个半平面γ,使二面角 α-a-γ为45°,二面角γ-a-β为30°,则γ内的任意
一 点P到平面α与平面β的距离之比为( )
(A) (B)
(C) (D)基础题例题返回基础题例题5. PA、PB、PC是从P点引出的三条射线,每两条的夹角
都是60o,则二面角B –PA—C的余弦值是 ( )
A. B. C. D.AD返回ABCA′M已知:如图⊿ABC的顶点A在平面M上的射影为点A′, ⊿ABC的面积是S, ⊿A′BC的面积是S′,设二面角A-BC-A′为?.求证:COS ? = S ′÷ S返回在正方体AC1中,求二面角D1-AC-D的大小?返回 过正方形ABCD的顶点A引SA⊥底面ABCD,并使平面SBC,SCD都与底面ABCD成45度角,求二面角B-SC-D的大小.E返回7.已知斜三棱柱ABC—A1B1C1中,∠BCA=90°,AC=
BC,A1在底面ABC的射影恰为AC的中点M. 又知AA1
与底面ABC所成的角为60°.
(1)求证:BC⊥平面AA1C1C;
(2)求二面角B-AA1-C的大小.能力·思维·方法返回7.已知斜三棱柱ABC—A1B1C1中,∠BCA=90°,AC=BC,A1在底面ABC的射影恰为AC的中点M. 又知AA1与底面ABC所成的角为60.(1)求证:BC⊥平面AA1C1C;(2)求二面角
B-AA1-C的大小.能力·思维·方法证明: (1)由题设知,A1M⊥平面ABC,又A1M 平面AA1C1C,∴(1)平面AA1C1C⊥底面ABC,又BC⊥AC,平面AA1C1C∩平面ABC=AC,∴BC ⊥平面AA1C1C返回7.已知斜三棱柱ABC—A1B1C1中,∠BCA=90°,AC=BC,A1在底面ABC的射影恰为AC的中点M. 又知AA1与底面ABC所成的角为60.(1)求证:BC⊥平面AA1C1C;(2)求二面角
B-AA1-C的大小.能力·思维·方法证明: (2)由题设知,A1M⊥平面ABC,∴AA1与底面ABC所成角为∠A1AC,∴∠A1AC=60o,又M是AC中点,∴△AA1C是正三角形,作CN⊥AA1于N,∴点N是AA1的中点,连接BN,由BC ⊥平面AA1C1C,∴BC⊥AA1,∴作AA1 ⊥平面BNC,∴AA1 ⊥BN ,∴∠BNC是二面角B--AA1—C的平面角,返回7.已知斜三棱柱ABC—A1B1C1中,∠BCA=90°,AC=BC,A1在底面ABC的射影恰为AC的中点M. 又知AA1与底面ABC所成的角为60.(1)求证:BC⊥平面AA1C1C;(2)求二面角
B-AA1-C的大小.能力·思维·方法设AC=BC=a,正三角形AA1C的边长为a,∴在直角三角形BNC中,∴二面角B—AA1—C的大小是返回【解题回顾】①先由第(1)小题的结论易知BC⊥AA1,
再利用作出棱AA1的垂面BNC来确定平面角∠BNC.
②将题设中“AA1与底面ABC所成的角为60°”改为 “ BA1⊥AC1 ” 仍可证得三角形AA1C为正三角形,所求 二面角仍为 .
③本题的解答也可利用三垂线定理来推理.能力·思维·方法返回在正方体AC1中,E,F分别是AB,AD的中点,求二面角C1-EF-C的大小?EFABDCA1B1D1C1H返回⊿ABC中,AB⊥BC,SA ⊥平面ABC,DE垂直平分SC,又SA=AB,SB=BC,求二面角E-BD-C的大小?SABCED返回求正四面体的侧面与底面所成的二面角的大小?E返回三棱锥P-ABC中,PA ⊥平面ABC,PA=3,AC=4,PB=PC=BC. (1)求二面角P-BC-A的大小34H返回 (2)求二面角A-PC-B的大小COS ?=三棱锥P-ABC中,PA ⊥平面ABC,PA=3,AC=4,PB=PC=BC. (1)求二面角P-BC-A的大小返回在正方体AC1中,E,F分别是中点,求截面A1ECF和底面ABCD所成的锐二面角的大小.EF返回EF在正方体AC1中,E,F分别是中点,求截面A1ECF和底面ABCD所成的锐二面角的大小.返回例: 如图ABC-A1B1C1是各条棱长均为2的正三棱柱, (1)求 AB1与A1C所成角?(2)求AB1与平面BB1C1C所成角?(3) 若点D是侧棱CC1的中点,求平面AB1D与平面ABC所成角?
A1AB1C1BC返回例: 如图ABC-A1B1C1是各条棱长均为2的正三棱柱, (1)求 AB1与A1C所成角?返回解: 分别取A1A,AC, A1B1的中点N,M, G,连接GN,NM.则∠GNM为所求角.并连接GM.GM每条棱长为2GM= 所求角大小为:arccosN返回1. 如图ABC-A1B1C1是各条棱长均为2的正三棱柱, (1)求 AB1与A1C所成角?(2)求AB1与平面BB1C1C所成角?E所求角大小为:arcsin返回例: 如图ABC-A1B1C1是各条棱长均为2的正三棱柱,(3) 若点D是侧棱CC1的中点,求平面AB1D与平面ABC所成角?A1AB1C1BCD返回则:AG所求角大小为:返回A1AB1C1BCDM ∠B1AB为二面角B1-AM-B的平面角.返回 解:延长B1D交BC延长线于M,连接AMCM=CB=CA所求角大小为:点D是CC1的中点,且CD//BB1返回CABDA1B1C1D1MN返回CABDA1B1C1D1MN返回CABDA1B1C1D1MN返回CABDA1B1C1D1MN返回CABDA1B1C1D1MN返回CABDA1B1C1D1MN返回返回B1A1C1 ABC例: 在直三棱柱ABC-A1 B1 C1中, ∠ BAC=90o,AB=BB1=1,直线B1C与平面ABC成30o 的角,
求二面角B-B1C - A的余弦值。分析:求二面角B- B1C-A的度数,要作出平面角,显然二面
角的棱为B1C,故需在B1C上取一点,然后分别在两个面内作垂
直于棱的两条射线。返回C1 AA1B1BC返回1.熟练掌握求二面角大小的基本方法:(1)先作平面角,再求其大小;
(2)直接用公式2.掌握下列两类题型的解法:(1)折叠问题——将平面图形翻折成空间图形.(2)“无棱”二面角——在已知图形中未给出二面角的棱.返回基础题例题二面角α-AB-β的平面角是锐角,C是平面α内的
点(不在棱AB上),D是C在平面β上的射影,E是棱
AB上满足∠CEB为锐角的任意一点,则( )
(A)∠CEB>∠DEB (B)∠CEB=∠DEB
(C)∠CEB<∠DEB
(D)∠CEB与∠DEB的大小关系不能确定A返回2. 直线AB与直二面角α-l-β的两个半平面分别交于A、B两点,且A、B l. 如果直线AB与α、β所成的角 分别是θ1、θ2,则θ1+θ2的取值范围是( )
(A)
(B)
(C)
(D)D基础题例题返回在长、宽、高分别为1、1、2的长方体ABCD-A1B1
C1D1中,截面BA1C1与底面ABCD所成角的余弦值是__
_____.4. 把边长为a的正三角形ABC沿着过重心G且与BC平 行的直线折成二面角,此时A点变为 ,当
时,则此二面角的大小为__________________.arccos(1/3)基础题例题返回5.已知正方形ABCD中,AC、BD相交于O点,若将正方
形ABCD沿对角线BD折成60°的二面角后,给出下面4个
结论:
①AC⊥BD;②AD⊥CO;③△AOC为正三角形;
④过B点作直线l⊥平面BCD,则直线l∥平面AOC,
其中正确命题的序号是________①③④基础题例题返回6. 在四面体P—ABC中,PC⊥平面ABC,
AB=BC=CA=PC,求二面角B—AP—C的大小. EF解:如图过B作BE⊥AC于E,过E作EF⊥PA于F,连结BF。
∵PC⊥平面ABC,∴BE⊥平面PAC,∴BF⊥PA。
∴∠BFE就是二面角B―PA―C的平面角。设PC=1 则AB=BC=CA=PC=1,
∴E为AC的中点,∴所求二面角大小为: 能力·思维·方法………………返回能力·思维·方法7.平面四边形ABCD中,AB=BC=CD=a,∠B=90°,∠DCB=135°,沿对角线AC将四边形折成直二面角.
证:(1)AB⊥面BCD;(2)求面ABD与面ACD所成的角.返回能力·思维·方法7.平面四边形ABCD中,AB=BC=CD=a,∠B=90°,∠DCB=135°,沿对角线AC将四边形折成直二面角.
证:(1)AB⊥面BCD;(2)求面ABD与面ACD所成的角.证明: (1)D-AC-B是直二面角,又∵DC⊥AC,∴DC⊥平面ABC,(面面垂直性质定理)又AB 平面ABC,∴DC⊥AB,又AB⊥BC,∴AB⊥平面BCDABCD返回能力·思维·方法7.平面四边形ABCD中,AB=BC=CD=a,∠B=90°,∠DCB=135°,沿对角线AC将四边形折成直二面角.
证:(1)AB⊥面BCD;(2)求面ABD与面ACD所成的角.证明: (2)过C作CH⊥DB于H,∴平面ABD⊥平面DCB,∴CH⊥平面ABD,∵AB⊥平面BCD又∵平面ABD ∩平面DCB=DB,BH过H作HE⊥AD于E,E连接CE,由三垂线定理知 CE⊥ADHE⊥ADCE⊥AD∴∠CEH是所求二面角
的平面角,∴∠CEH=60o,即所求二面角为 60o返回【解题回顾】准确画出折叠后的图形,弄清有关点、 线之间的位置关系,便可知这是一个常见空间图形 (四个面都是直角三角形的四面体).能力·思维·方法返回例.A为二面角α-l-β的棱l上一点,射线AB α,且与棱成45°角,与β成30°角,则二面角α-l-β的大小是( )。(A)45° (B)30° (C)45°或135° (D)30°或150°提示:分锐二面角和钝二面角两种情况讨论返回∴sin∠BCD=
∴ ∠BCD=45°,返回如图(2),若二面角α-l-β是钝二面角,自B作BD⊥β,D为垂足,作BC⊥l于C,C为垂足,连接CD,延长DC到E,则由三垂线定理得CE⊥l,∴ ∠BCE是二面角α-l-β的平面角,而∠BCD是二面角α-l-β的平面角的补角,由(1)解得∠BCD=45°,
∴ ∠BCE=135°,
即二面角的大小是45°或135°,选C. 返回8.在直角梯形P1DCB中,P1D∥CB,CD⊥P1D,P1D=
6,BC=3,DC=3,A是P1D的中点. 沿AB把平面P1AB折起到平面PAB的位置,使二面角P-CD-B成45°,设E、F分别为AB、PD的中点.
(1)求证:AF∥平面PEC;
(2)求二面角P-BC-A的大小;能力·思维·方法EFP..证明:(1)取PC的中点G,.G连接FG、EG,则FG//CD,且FG= CD,∵AE//CD,且AE= CD∴AE//FG,AE=FG,从而四边形AEGF是平行四边形,∴AF//EG,EG 平面PEC,∴AF//平面PEC返回8.在直角梯形P1DCB中,P1D∥CB,CD⊥P1D,P1D=
6,BC=3,DC=3,A是P1D的中点. 沿AB把平面P1AB折起到平面PAB的位置,使二面角P-CD-B成45°,设E、F分别为AB、PD的中点.
(1)求证:AF∥平面PEC;
(2)求二面角P-BC-A的大小;能力·思维·方法P证明:(2)∵CD⊥平面PAD,∴平面PAD⊥平面ABCD∴∠PAB为二面角P-BC-A的平面角,在Rt△PAB中,PA=3,PB= ,∵PA=AD,且∠PDA=45o,∴PA⊥AD∴PA⊥平面ABCD,∴AB⊥BC由三垂线定理得 PB⊥BC∴sin∠PBA=得所求的二面角为60o返回【解题回顾】找二面角的平面角时不要盲目去作,而
应首先由题设去分析,题目中是否已有.能力·思维·方法返回9.正方体ABCD—A1B1C1D1中,E是BC的中点,求平面B1D1E和平面ABCD所成的二面角的正弦值.能力·思维·方法ADBCB1A1D1C1.E解题分析:所求二面角”无棱”,要么先找 “棱”,要么用面积投影.解法一:取B1C1的中点M,.M连接EM,∵E为BC的中点,∴EM⊥平面A1B1D1,∴△B1D1 M是△D1B1E的射影三角形,设平面B1D1E和平面A1B1C1D1所成的
二面角为α,∵平面ABCD//平面A1B1C1D1,∴平面B1D1E和平面ABCD所成的
二面角也为α,设正方体棱长为 a,∴所求二面角的正弦值为返回9.正方体ABCD—A1B1C1D1中,E是BC的中点,求平面B1D1E和平面ABCD所成的二面角的正弦值.能力·思维·方法ADBCB1A1D1C1.F解法二:取BC的中点F,.M连接BD、EF,∴所求二面角的正弦值为.E∵E为BC的中点,∴EF//BD,∵BD//B1D1,∴EF//B1D1,∴EF、B1D1共面,∴平面ABCD∩平面EB1D1F=EF,作BG⊥EF交FE的延长线于G,G连接B1G,则∠B1GB是平面B1D1E和平面ABCD所成二面角的平面角。设正方体棱长为 a,则BE= ,BG= ,在Rt△B1BG中,B1G= ,返回【解题回顾】解法一利用公式 . 思路简单明
了,但计算量较解法二大.解法二的关键是确定二 面角的棱,再通过三垂线定理作出平面角,最终解直 角三角形可求出.能力·思维·方法返回例:如图,已知在正三棱柱ABC-A1B1C1中,侧棱长大于底面边长,M、N分别在侧棱AA1、BB1上,且B1N=A1B1=2A1M,求截面C1MN与底面A1B1C1所成的二面角的大小。返回返回例:S是正△ABC所在平面外一点,SA=SB=SC且∠ASB=∠BSC=∠CSA=90°,M,N分别是AB和SC的中点,求异面直线SM与BN所成的角的余弦值.Paaa返回距离问题一、知识概念1.距离定义
(1)点到直线距离
从直线外一点引一条直线的垂线,这点和垂足之间的距离叫这点到这条直线的距离。
(2)点到平面的距离
从平面外一点引一个平面的垂线,这点和垂足之间的距离叫这点到这个平面的距离。
(3)两平行直线间的距离
两条平行线间的公垂线段的长,叫做两条平行线间的距离。返回(4)两条异面直线间的距离
和两条异面直线分别垂直相交的直线,叫两条异面直线的公垂线;公垂线上夹在两异面直线间的线段的长度,叫两异面直线的距离。
(5)直线与平面的距离
如果一条直线和一个平面平行,那么直线上各点到这个平面的距离相等,且这条直线上任意一点到平面的距离叫做这条直线和平面的距离。
(6)两平行平面间的距离
和两个平行平面同时垂直的直线,叫这两个平行平面的公垂线,它夹在两个平行平面间的公垂线段的长叫做这两个平行平面间的距离。返回2.求距离的步骤
(1)找出或作出有关距离的图形
(2)证明它们符合定义
(3)在平面图形内进行计算返回ABCA1B1D1C1正方体AC1的棱长为1,求下列距离问题(1)A到CD1的距离D点—线返回ABCA1B1D1C1正方体AC1的棱长为1,求下列距离问题(1)A到CD1的距离D(2)A到BD1的距离返回点—线ABCDA1B1C1D1H已知:长方体AC1中,AB=a,AA1=AD=b求点C1到BD的距离?C1H=返回线—线ABCDEF矩形CDFE和矩形ABFE所在的平面相交,EF=5,AD=13,求平行线AB和CD的距离?返回点—面从平面外一点引这个平面的垂线垂足叫做点在这个平面内的射影这个点和垂足间的距离叫做点到平面的距离线面垂直点的射影点面距离返回已知三棱锥P-ABC的三条侧棱PA=PB=PC
试判断点P在底面ABC的射影的位置?PABCOOA=OB=OCO为三角形ABC的外心返回已知三棱锥P-ABC的三条侧棱PA,PB,PC两两垂直,试判断点P在底面ABC的射影的位置?PABCO为三角形ABC的垂心DO返回已知三棱锥P-ABC的顶点P到底面三角形ABC的三条边的距离相等,试判断点P在底面ABC的射影的位置?PABCO为三角形ABC的内心OEF返回已知三棱锥P-ABC的三条侧棱PA=PB=PC
试判断点P在底面ABC的射影的位置?外心已知三棱锥P-ABC的三条侧棱PA,PB,PC两两垂直,试判断点P在底面ABC的射影的位置?垂心已知三棱锥P-ABC的顶点P到底面三角形ABC的三条边的距离相等,试判断点P在底面ABC的射影的位置?内心PABCO返回ABCA1B1D1C1正方体AC1的棱长为1,求下列距离问题D(1)A到面A1B1CD返回ABCA1B1D1C1正方体AC1的棱长为1,求下列距离问题D(1)A到面A1B1CD(2)A到平面BB1D1返回棱长为1的正四面体P——ABC中,求点P到平面ABC的距离?ABCOP返回4.如图,已知P为△ABC外一点,PA、PB、PC两两垂直,且PA=PB=PC=3,求P点到平面ABC的距离。返回3.如图,AB是⊙O的直径,PA⊥平面⊙O,C为圆周上一点,若AB=5,AC=2,求B到平面PAC的距离。返回直角三角形ACB确定平面 ? ,点P在平面 ? 外,
若点P到直角顶点C的距离是24,到两直角边的
距离都是6 ,求点P到平面 ? 的距离?PABCEFO?返回ABEFDCPZ返回线—面一条直线和一个平面平行时,直线上任意一点
到这个平面的距离叫做直线到平面的距离返回例:已知一条直线 l 和一个平面?平行,求证:直线 l 上各点到平面?的距离相等?AA`BB`l返回?lA`AB返回如果一条直线上有两个点到平面的距离
相等,则这条直线和平面平行吗?判断题:返回空间四面体ABCD,问和点A,B,C,D
距离相等的平面有几个?ABCD4ABCD3返回5.如图,已知在长方体ABCD-A’B’C’D’中,棱AA’=5,AB=12,求直线B’C’到平面A’BCD’的距离。练 习返回ABCDPFE已知:ABCD是边长为4的正方形,E,F分别是
AD,AB的中点,PC⊥面ABCD,PC=2,
求点B到平面PEF的距离?GOH点—线点—面线—面综合练习:返回例3:如图:已知ABCD是边长为4的正方形,E、F分别是AB、AD的中点,PC垂直平面ABCD,且PC=2,求点B到平面EFP的距离。解:连AC,BD,设交于O,设AC交EF于HOH连PH因为BD∥平面PEF,所以求B到平面的距离,可转化为求BD到平面的距离过O作OK⊥平面PEF,可证明OK就是所要求的距离K此时,得用△OKH∽△PCH,容易求得 OK的值。返回两个平行平面的距离ABA’B’ 和两个平行平面同时垂直的直线,叫做这两个平面的公垂线。 公垂线夹在平行平面间的部分,叫做这两个平面的公垂线段。直线AA’、BB’都是它们的公垂线段 两个平行平面的公垂线段的长度,叫做两个平行平面的距离。返回返回题型讲练:思考:在边长为1的正方体 中,M,N,E,F分别放 飞 思 维 的 翅 膀 是棱 的中点.(1)求证:平面 面 ;(2)求:平面 与面 的距离.返回思考题:(1999)如图:已知正四棱柱ABCD-A’B’C’D’中,点E在棱DD’上,截面EAC∥D’B,且面EAC与底面ABCD所成的角为450,AB=a
(1)求截面EAC的面积
(2)求异面直线A’B’与AC的距离返回二、例例1:在600二面角M-α-N内有一点P,P到平面M、平面N的距离分别为1和2,求P到直线a距离。解:设PA,PB分别垂直平面M,平面N与A、B,PA,PB所确定的平面为α,且平面α交直线a与Q,设PQ=x在直角△PAQ中sin∠AQP=1/x
在RT △PBQ中sin ∠AQP=2/xcos600=cos(∠AQP +∠AQP),由此可得关于x的方程最后可解得返回例2:菱形ABCD中,∠BAD=600,AB=10,PA⊥平面ABCD,且PA=5,求:
(1)P到CD的距离
(2)P到BD的距离
(3)P到AD的距离
(4)求PC的中点到
平面PAD的距离(1)过P作CD的垂线,交CD的延长线于E,连AEE(2)连BD,交AC于O,连POO返回1. α、β是两个平行平面,aìα,bìβ ,a与b之 间的距离为d1, α与β之间的距离为d2,则 ( )
(A)d1=d2 (B)d1>d2 (C)d1<d2 (D)d1≥d2基础题例题D2. 一副三角板如图拼接,使两个三角板所在的平面互 相垂直.如果公共边AC=a,则异面直线AB与CD的距离 是 ( )
(A) (B) a
(C) (D)C返回3. △ABC中,AB=9,AC=15,∠BAC=120°,△ABC
所在平面外一点P到三个顶点A、B、C的距离都是14,
那么点P到平面α的距离为 ( )
(A)7 (B)9 (C)11 (D)13A基础题例题4. 在长方体, 中,已知AB=4,AA1
=3,AD=1,则点C1到直线A1B的距离为_________.返回5.已知Rt△ABC的直角顶点C在平面α内,斜边 AB∥α,AB=2√6,AC、BC分别和平面α成45°和 30°角,则AB到平面α的距离为______.2基础题例题6.在二面角α- l –β的半平面α内有一点 A 到棱 l 的距
离为 2 ,到半面β所在平面的距离等于 1 ,则这个二面角
的度数为__________________30o 或 150o返回2.已知四面体ABCD,AB=AC=AD=6,BC=3,CD=4,BD=5,求点A到平面BCD的距离。练习:ABD返回7.平面α内的∠MON=60°,PO是平面α的斜线段,PO=3,且PO与∠MON的两边都成45°的角,则点P到α的距离为 ( )
A. B. C. D.A基础题例题8.直线 EF 平行于平面α内的两条直线AB和CD,EF
与α的距离为15,与AB的距离为17,又AB与CD的距
离是28,则EF与CD的距离是 .25或39返回9. 已知平面α∥β, AB⊥α, AB⊥β, A α, B β ,直线 a α,b β, a∥b,A到 a 的距离为2,B 到 b 的距离为5,AB=4,则a,b间的距离为 . 基础题例题ababαβαβABAB返回11.在棱长为1的正方体 中,
(1)求点A到平面 的距离;
(2)求点 到平面 的距离;
(3)求平面 与平面 的距离;
(4)求直线AB与平面 的距离.能力·思维·方法ACDBA1B1D1C1O 解析:
连AC、BD交于O,
AO⊥BD,
又AO⊥DD1,
∴AO⊥平面BD1,
AO的长即为所求返回11.在棱长为1的正方体 中,
(1)求点A到平面 的距离;
(2)求点 到平面 的距离;
(3)求平面 与平面 的距离;
(4)求直线AB与平面 的距离.能力·思维·方法ACDBA1B1D1C1O’E易知平面
A1ACC1⊥平面AB1D1
在矩形AA1CC1中,
易知A1 C⊥O1A
设A1E⊥AO1于E,
∴A1E⊥平面AB1 D1
∴A1E为所求。返回11.在棱长为1的正方体 中,
(1)求点A到平面 的距离;
(2)求点 到平面 的距离;
(3)求平面 与平面 的距离;
(4)求直线AB与平面 的距离.能力·思维·方法ACDBA1B1D1C1EF..易知A1C⊥平面AB1D1
A1C⊥平面BC1D
设直线A1C分别交平
面AB1D1、平面BC1D于
点E、F,则EF的长为
所求
返回11.在棱长为1的正方体 中,
(1)求点A到平面 的距离;
(2)求点 到平面 的距离;
(3)求平面 与平面 的距离;
(4)求直线AB与平面 的距离.能力·思维·方法ACDBA1B1D1C1G.因为直线AB∥平面CDA1B1
∴点B到平面CDA1B1 的距
离BG就是所求的距离,
(G是BC1与B1C的交点,
BG⊥B1C, BG⊥CD,
∴直线BG⊥平面A1B1CD)
此距离为: 返回【解题回顾】(1)求距离的一般步骤是:一作,二证,三计算.即先作出表示距离的线段,再证明它就是要求的距离,然后再计算,其中第二步的证明易被忽视,应引起重视.
(2)求距离问题体现了化归与转化的思想,一般情况下需要转化为解三角形.能力·思维·方法返回12. 已知如图,边长为a的菱形ABCD中,∠ABC=60°,PC⊥平面ABCD,E是PA的中点,求E到平面PBC的距离.能力·思维·方法解:∵E是PA的中点,∴E到平面PBC的距离等于A 到
平面PBC的距离的一半.由PC⊥平面ABCD,得到平面PBC⊥平面ABCD在平面ABCD内作AH⊥BC,
交BC于H,则AH= H所求距离为 返回12. 已知如图,边长为a的菱形ABCD中,∠ABC=60°,PC⊥平面ABCD,E是PA的中点,求E到平面PBC的距离.能力·思维·方法GO返回 距离离不开垂直,因此求距离问题的过程实质上是
论证线面关系(平面与垂直)与解三角形的过程,值得注
意的是,“作、证、算、答”是立体几何计算题不可缺少
的步骤,尤其是证明那一步.误解分析返回13. 在120°的二面角 内有一点P,它到二面角的两个面的距离分别是3cm和4cm,求它在α和β内的射影的距离和这点到 l 的距离.能力·思维·方法解析:设P到α、β的射影分别是M、N,则
PM=3cm,PN=4cm,过P、M、N作平面γ交l于Q则
l⊥γ∴l⊥QM,l⊥QN
∴∠MQN为二面角α-l-β的平面角。
∴∠MQN=120°
∴∠M+∠N=180°
∴P、M、Q、N四点共圆,
∴∠MPN=180°-120°=60°P到 l 的距离是: MN=返回棱柱问题棱锥问题复习:知识网络底面对角线高侧面侧棱顶点棱柱(概念)有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行的几何体。体积V=Sh返回复习:知识网络棱柱(分类)斜棱柱
直棱柱正棱柱返回复习:知识网络四棱柱四棱柱直四棱柱
侧棱垂直底面平行六面体
底面是平行四边形长方体正四棱柱正方体侧面垂直底面返回要点·疑点·考点一、棱柱(1)有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面围成的几何体叫棱柱 1.概念(2)侧棱不垂直于底面的棱柱叫斜棱柱,侧棱垂直于底面的棱柱叫直棱柱,底面是正多边形的直棱柱叫正棱柱 返回(2)两个底面与平行于底面的截面是全等的多边形;2.性质(3)过不相邻的两条侧棱的截面是平行四边形.(1)侧棱都相等,侧面是平行四边形;要点·疑点·考点3.长方体及其相关概念、性质(1)概念:底面是平行四边形的四棱柱叫平行六面体.
侧棱与底面垂直的平行六面体叫直平行六面体.
底面是矩形的直平行六面体叫长方体.
棱长都相等的长方体叫正方体.(2)性质:设长方体的长、宽、高分别为a、b、c,
对角线长为l ,则l2=a2+b2+c2返回复习:知识网络棱锥棱锥正四棱锥正三棱锥正四面体体积V=Sh/3顶点在底面正多边形的射影是底面的中心返回复习:重要定理三垂线定理(逆)作用:1 证明线线垂直;
2 作二面角的平面角。一作一连法返回棱锥基本性质如果棱锥被平行于底面的平面所截,那么截面和底面相似,并且它们面积的比等于截得的棱锥的高与已知棱锥的高的平方比返回棱锥基本性质棱锥的高、斜高和斜高在底面的射影组成一个直角三角形。棱锥的高、侧棱和侧棱在底面的射影组成一个直角三角形PCBDARt⊿ PEHRt⊿ PHBRt⊿ PEBRt⊿ BEH返回正棱锥如果一个棱锥 的底面是正多边形,并且顶点在底面的射影是底面中心这样的棱锥叫做正棱锥返回1、侧面与底面所成的角都相等的棱锥是正棱锥2、棱锥的高可以等于它的一条侧棱长3、棱锥的高一定在棱锥的内部4、侧面均为全等的等腰三角形的棱锥是正棱锥判断正误返回1、三条侧棱相等2、侧棱与底面所成的角相等3、侧面与底面所成的角相等4、顶点P到⊿ABC的三边距离相等5、三条侧棱两两垂直6、相对棱互相垂直7、三个侧面两两垂直外心外心内心内心垂心垂心垂心返回有没有侧棱长和底面边长相等的正四棱锥?有没有侧棱长和底面边长相等的正五棱锥?有没有侧棱长和底面边长相等的正六棱锥?返回1.一个三棱锥,如果它的底面是直角三角形,那么它的三个侧面( )
(A)至多只有一个是直角三角形
(B)至多只有两个是直角三角形
(C)可能都是直角三角形
(D)必然都是非直角三角形C基础题例题返回2.命题:
①底面是正多边形的棱锥,一定是正棱锥;
②所有的侧棱的长都相等的棱锥,一定是正棱锥;
③各侧面和底面所成的二面角都相等的棱锥,一定是正棱锥;
④底面多边形内接于一个圆的棱锥,它的侧棱长都相等;
⑤一个棱锥可以有两条侧棱和底面垂直;
⑥一个棱锥可以有两个侧面和底面垂直.
其中正确的有 ( )
(A)0个 (B)1个 (C)3个 (D)5个C基础题例题返回基础题例题2.正三棱柱ABC-A1B1C1中,若AB=√2 BB1,则AB1
与C1B所成角的大小是 ( )
A.60o B.90o C.105o D.75o
B返回3.长方体三边之和为a+b+c=6,总面积为11,则 其对角线长为__;若一条对角线与二个面所成的 角为30°或45°,则与另一个面所成的角为 ___;若一条对角线与各条棱所成的角为α、 β、γ,则sinα、sinβ、sinγ的关系为_____
___________________________.sin2α+sin2β+sin2γ=2基础题例题530°返回设棱锥的底面积是8cm2,则这个棱锥的中截面(过棱锥的高的中点且平行于底面的截面)的面积是多少?S中=2返回过棱锥的高的三等分点作两个平行于底面的截面,它将棱锥的侧面分为三部分面积之比(自上而下)为 。返回过棱锥的高作两个平行于底面的截面,它将棱锥的侧面分为三部分面积相等则它分棱锥的高的比是(自上而下) 。返回正三棱锥的底面边长为a.侧棱长为b,求它的高和侧面积?PABCO返回正三棱锥的底面边长为1.侧面与底面所成的角为60,求它的高和相邻两侧面所成的二面角的大小?PABCO返回正四棱锥的底面边长为1.侧面与底面所成的角为60,求它的高和相邻两侧面所成的二面角的大小?PABDCO返回正三棱锥的底面边长为a .侧棱与底面所成的角为60,过底面一边做一截面使其与底面成30的二面角,求此截面面积?PABCO返回 已知:三棱锥P-ABC的底面是等腰三角形,AB=AC=10,BC=12,棱锥的侧面与底面所成的二面角都是45,求棱锥的侧面积?返回连接棱长都是a的正三棱锥的侧面中心成一个三角形,求此三角形的面积?PABC返回在正四棱锥内有一个内接正方体,这正方体的四个顶点在四棱锥的侧棱上,另四个顶点在棱锥底面上,若棱锥底面边长为a,高为h,求内接正方体的棱长?ABDCOPH设内接正方体的棱长为x返回在正三棱锥P-ABC的底面边长和高都是4,其内接正三棱柱的三个侧面都是正方形,求内接正三棱柱的全面积?返回能力·思维·方法4. 在底面是直角梯形的四棱锥P-ABCD中,
侧棱PA⊥底面ABCD,∠ABC=90°,PA=AB=BC=2,AD=1, (1)求D到平面PBC的距离;
(2)求面PAB与面PCD所成的二面角的大小。?解: (1)∵AD//平面PBC∴D到平面PBC的距离等于A到平面PBC的距离∵PA⊥BC, AB⊥BC∴BC⊥平面PAB∴平面PBC⊥平面PAB∴A到PB的距离就是A到平面PBC的距离∵PA=AB=2, PA⊥AB,∴A到PB的距离为∴D到平面PBC的距离为返回能力·思维·方法4. 在底面是直角梯形的四棱锥P-ABCD中,
侧棱PA⊥底面ABCD,∠ABC=90°,PA=AB=BC=2,AD=1, (1)求D到平面PBC的距离;
(2)求面PAB与面PCD所成的二面角的大小。?Q (2)延长CD与BA相交于Q,∵AD∥BC,且 AD= BC∴A是QB的中点,又PA=AB=AQ∴BQ⊥PQ,又∵BC⊥平面PAB,∴CP⊥PQ,故∠CPB是所求二面角的
平面角,故面PCD与面PCD所成的二面角为返回例题讲解1、四棱锥P-ABCD的底面是边长为a的正方形,PB⊥面ABCD.
(1)若面PAD与面ABCD的二面角为600,求四棱锥的体积;作、证、求?∵ PB⊥面ABCD,BA⊥AD, ∴PA⊥AD ∴∠PAB就是面PAD与面ABCD的二面角的平面角解:即∠PAB=600V= a3返回例题讲解1、四棱锥P-ABCD的底面是边长为a的正方形,PB⊥面ABCD.
(2)证明不论高PB怎样变化,面PAD与面PCD所成的二面角恒大于900.M证:由题设侧面PAD与PCD为全等⊿,作CM⊥PD于M,连结MA,则⊿CDM≌⊿ADM,∴AM=CM,∠AMD=900故AMC就是所证二面角的平面角.连结AC在⊿AMC中,由余弦定理
cos∠AMC =故∠AMC>900,即证. 小结:作二面角平面角的方法
●有面的垂线,则一作一连法
●定义法,在两面内作棱的垂线
●面积射影定理返回变化一 四棱锥P-ABCD的底面是边长为a的菱形,∠BCD=600,PB⊥面ABCD.若面PAD与面ABCD的二面角为600,求四棱锥的体积;E返回 四棱锥P-ABCD的底面是边长为a的菱形,∠BCD=600,面PBC⊥面ABCD,且⊿PBC是等边⊿. 求侧面PAD与底面ABCD所成的二面角;变化二E注意:●面面垂直的应用
●分析平面图形返回例题讲解2、如图在直三棱柱ABC-A1B1C1中,底面ABC是等腰Rt⊿, ∠C=900 ,D、E分别是CC1和A1B的中点,AC=AA1=2
(1)求线段DE的长返回例题讲解2、如图在直三棱柱ABC-A1B1C1中,底面ABC是等腰Rt⊿, ∠C=900 ,D、E分别是CC1和A1B的中点,AC=AA1=2
(2)求二面角A-BD-C的大小(反三角表示)解:∵ ABC-A1B1C1是直棱柱,AC⊥BC,∴AC⊥侧面BB1C1C,作CM⊥BD于M,连结AM,则∠AMC就是所求二面角的平面角;在⊿ACM中,AC=2∴tan∠AMC=AC/CM=即所求为AC⊥CM,返回例题讲解3、如图在直三棱柱ABC-A1B1C1中,底面ABC是等腰Rt⊿,∠C=900 ,D、E分别是CC1和A1B的中点,AA1=2,若点E在平面ABD上的射影是⊿ABD的重心G.
(1)求A1B与平面ABD所成的角(用反三角表示);解:连结BG,由已知∠EBG就是所求的角,…… ……∴A1B与平面ABD所成的角为返回例题讲解3、如图在直三棱柱ABC-A1B1C1中,底面ABC是等腰Rt⊿,∠C=900 ,D、E分别是CC1和A1B的中点,AA1=2,若点E在平面ABD上的射影是⊿ABD的重心G.
(2)求点A1到平面AED的距离。方法A:作垂线法方法B:等体积法返回3、如图在直三棱柱ABC-A1B1C1中,底面ABC是等腰Rt⊿,∠C=900 ,D、E分别是CC1和A1B的中点,AA1=2,若点E在平面ABD上的射影是⊿ABD的重心G.
(2)求点A1到平面AED的距离。解A:由上题解知,DE⊥平面AA1B1B∴平面ADE⊥平面AA1B1B于AE在⊿A1AB1中,A1K=方法A:作垂线法返回3、如图在直三棱柱ABC-A1B1C1中,底面ABC是等腰Rt⊿,∠C=900 ,D、E分别是CC1和A1B的中点,AA1=2,若点E在平面ABD上的射影是⊿ABD的重心G.
(2)求点A1到平面AED的距离。解B:方法B:等体积法方法C:对象转换法返回小结:1、联想概念及其性质;
2、分解难点,掌握各类基本作图;
3、强调作证求过程;
4、空间问题平面化,尤三角形内
的计算。返回面积问题体积问题返回返回返回基础题例题C1.设棱锥的底面面积为8cm2,那么这个棱锥的中截面
(过棱锥的中点且平行于底面的截面)的面积是( )
(A)4cm2 (B) cm2 (C)2cm2 (D) cm22. 一个锥体被平行于底面的平面所截,若截面面积 是底面面积的四分之一,则锥体被截面截得的一个小 锥与原棱锥体积之比为 ( )
(A)1 : 4 (B) 1 : 3 (C) 1 : 8 (D) 1 : 7 C返回A3.设长方体三条棱长分别为a,b,c,若长方体所有棱的
长度之和为24,一条对角线长度为5 ,体积为2,则
等于 ( )
(A) (B) (C) (D)基础题例题返回C4.斜三棱柱的一个侧面的面积为S,另一条侧棱到这个
侧面的距离是a,则这个三棱柱的体积是 ( )
(A) (B) (C) (D)基础题例题5.在侧棱长为2√3,每个侧面的顶角均为40°的正三棱锥P-ABC中,过A作截面分别交PB、PC于E、F,则△AEF的最小周长是 ( )
(A) 6 (B) (C) 36 (D) A返回例.设P是棱长相等的四面体内任意一点,则P到各个面的距离之和是一个定值,这个定值等于( )。 (A)四面体的棱长 (B)四面体的斜高 (C)四面体的高 (D)四面体两对棱间的距离提示:用体积法求解 返回解:如图正四面体ABCD中,过点A作四面体的高AO,则由点P分别连接PA、PB、PC、PD,得到四个小四面体,
若点P到四个表面的距离分别为h1、h2、h3、h4,那么四面体被分成的四个小四面体,它们的体积和恰好是四面体ABCD的体积,返回∴ VABCD=VPBCD+VPABC+VPABD+VPACD,
∴
∴ h1+h2+h3+h4=AO. 选C.返回例.若正四棱柱的底面积为P,过相对两侧棱的截面面积是Q,则该四棱柱的体积是( )。 (A) (B) (C) (D)返回解:如图,设四棱柱底面边长AB=a,高AA1=b,则P=a2,过两侧棱AA1、CC1的截面面积Q= ab,∴ 返回6.若一个斜棱柱A1B1C1—ABC的底面是等腰△ABC,它的三边边长分别是AB=AC=10cm,BC=12cm,棱柱的顶点A1与A、B、C三点等距,且侧棱AA1=13cm,求此棱柱的全面积.解:自B引BD⊥AA1于D,连接CD,D∵AA1=A1B=A1C,底面△ABC为等腰△,故顶点A1在底面ABC上的射影O在底边
BC的高AE上,OE由三垂线定理知,BC⊥AA1,即侧面B1BCC1为矩形,由AA1⊥BC,AA1⊥BD,
得AA1⊥平面BDC,∴AA1⊥CD,在△A1AB中,引A1F⊥AB于F,F在Rt△A1FA中,由A1A=13,AF=5,A1F=12,得则BD=AB×sin∠A1AB=10×∴S柱侧=(BD+DC+BC)×A1A=396,又在△ABC中,AE⊥BC,AB=10,BE=6,得AE=8,∴S△ABC=8,∴S柱全=396+2×48=492(cm) 2返回7.已知E,F分别是棱长为a的正方体ABCD—A1B1C1D1的棱A1A,CC1的中点,求四棱锥C1—B1EDF的体积.能力·思维·方法...FE解:方法一:连接A1C1, B1D1交于O1,O1过O1作O1H⊥ B1D于H,H∵EF//A1C1, ∴A1C1//平面B1EDF ∴C1到平面B1EDF的距离 就是
A1C1就是 到平面B1EDF的距离∵平面B1D1D⊥平面B1EDF,∴O1H⊥平面B1EDF 即O1H为棱锥的高 ∵△B1O1H∽△B1DD1返回7.已知E,F分别是棱长为a的正方体ABCD—A1B1C1D1的棱A1A,CC1的中点,求四棱锥C1—B1EDF的体积.能力·思维·方法..FE解:方法二:连接EF设B1到平面C1EF的距离为h1,D到平面C1EF的距离为h2 ,则 h1+h2=B1D1=√2a , 返回7.已知E,F分别是棱长为a的正方体ABCD—A1B1C1D1的棱A1A,CC1的中点,求四棱锥C1—B1EDF的体积.能力·思维·方法..FE解:方法三:返回将边长为a的正方形ABCD沿对角线AC折起,使B,D两点间距离变为a,求所得三棱锥D-ABC的体积?ABCD返回将边长为a的正方形ABCD沿对角线AC折起,使B,D两点间距离变为a,求所得三棱锥D-ABC的体积?ABCD返回正方体ABCD-A1B1C1D1中,E,F分别是BB1,DD1的中点,棱长为a,求四棱锥D1-AEC1F的体积?EF返回平行六面体中,已知AB=AD=2a,AA1=a,∠ A1AD= ∠ A1AB= ∠ DAB= 60°(1)求证:AA1⊥面B1CD1A1B1C1D1ABCD返回A1B1C1D1ABCD平行六面体中,已知AB=AD=2a,AA1=a,∠ A1AD= ∠ A1AB= ∠ DAB= 60°(1)求证:AA1⊥面B1CD1返回(2)求平行六面体的体积?A1B1C1D1ABCDV= SA1B1CD1×CECE=SA1B1C1D1==平行六面体中,已知AB=AD=2a,AA1=a,∠ A1AD= ∠ A1AB= ∠ DAB= 60°(1)求证:AA1⊥面B1CD1返回A1B1C1D1ABCDS⊿B1CD1=VC1-B1CD1= S⊿B1CD1×CC1(2)求平行六面体的体积?平行六面体中,已知AB=AD=2a,AA1=a,∠ A1AD= ∠ A1AB= ∠ DAB= 60°(1)求证:AA1⊥面B1CD1返回A1B1C1D1ABCDS⊿B1CD1=VC1-B1CD1= S⊿B1CD1×CC1== S⊿B1C1D1×hV= ( 2 S⊿B1C1D1)×h(2)求平行六面体的体积?平行六面体中,已知AB=AD=2a,AA1=a,∠ A1AD= ∠ A1AB= ∠ DAB= 60°(1)求证:AA1⊥面B1CD1返回求多面体的体积时常用的方法直接法割补法变换法根据条件直接用柱体或锥体的体积公式如果一个多面体的体积直接用体积公式计算用困难,可将其分割成易求体积的几何体,逐块求积,然后求和。如果一个三棱锥的体积直接用体积公式计算用困难,可转换为等积的另一三棱锥,而这一三棱锥的底面面积和高都是容易求得返回求棱长为a的正四面体的体积.返回已知正三棱锥的侧面积是18 ,高为3,求它的体积?返回若正四棱锥的底面积是S,侧面积是Q,则它的体积为?返回过棱锥的高的三等分点作两个平行于底面的截面,它将棱锥分为三部分体积之比(自上而下)为 。返回PABC三棱锥P-ABC的三条侧棱两两垂直,PA=a, PB=b, PC=c , ⊿ABC的面积为S求点P到底面ABC的距离返回ABCDPFE已知:ABCD是边长为4的正方形,E,F分别是AD,AB的中点,PC⊥面ABCD,PC=2,
求点B到平面PEF的距离?GOH点—线点—面线—面返回ABCDPFEG= S⊿BFE×PC= S⊿PFE×h已知:ABCD是边长为4的正方形,E,F分别是AD,AB的中点,PC⊥面ABCD,PC=2,
求点B到平面PEF的距离?返回斜三棱柱ABC-A`B`C`的侧面BB`C`C的面积为S,AA`到此侧面的距离是a,求此三棱柱的体积?返回ABCA`B`C`斜三棱柱ABC-A`B`C`的侧面BB`C`C的面积为S,AA`到此侧面的距离是a,求此三棱柱的体积?返回如图,在多面体ABCDEF中,已知面ABCD是边长为3的正方形,EF//AB,EF=1.5, EF与面AC的距离为2,求此多面体的体积?=4.5=3返回=6=1.5如图,在多面体ABCDEF中,已知面ABCD是边长为3的正方形,EF//AB,EF=1.5, EF与面AC的距离为2,求此多面体的体积?返回正三棱柱ABC-A1B1C1的底面边长为3,侧棱长为4,求四面体ABB1C1的体积返回已知三棱锥有一条棱长为4,其余各棱长为3,求其体积?返回已知三棱锥有一条棱长为4,其余各棱长为3,求其体积?返回已知三棱锥P-ABC中,PA=1,AB=AC=2, ∠ PAB= ∠PAC= ∠BAC= 60°,求三棱锥的体积?返回已知三棱锥P-ABC中,PA=1,AB=AC=2, ∠ PAB= ∠PAC= ∠BAC= 60°,求三棱锥的体积?解法一直接法返回解法二变换法已知三棱锥P-ABC中,PA=1,AB=AC=2, ∠ PAB= ∠PAC= ∠BAC= 60°,求三棱锥的体积?返回解法三割补法已知三棱锥P-ABC中,PA=1,AB=AC=2, ∠ PAB= ∠PAC= ∠BAC= 60°,求三棱锥的体积?返回解法四割补法已知三棱锥P-ABC中,PA=1,AB=AC=2, ∠ PAB= ∠PAC= ∠BAC= 60°,求三棱锥的体积?返回例:如图已知正三棱锥S — ABC中,E、F分别是SB、SC 的中点,平面AEF⊥平面SCB.
求证:三棱锥S—ABC侧面 积与底面积的比。解:作正棱锥的高SO,连结AO并延长交BC于D,
连结SD交EF于G,连结AG.
GO返回设正三棱锥S—ABC的底面边长为 ,则AD= ,SA=SB=返回ABCSD例1、已知三棱锥的两个侧面都是边长为 的等边三角形,另一个侧面是等腰直角三角形。求此三棱锥的体积。法一:取AB中点D,连接SD,CD。
易得△ABC为等腰直角三角形,?ACB=90o。则有SD⊥AB,
CD⊥AB。又SA=SB=SC,
∴S在底面的射影为底面的外心,
即点D,∴SD⊥平面ABC。
∴由VS-ABC= S△ABC?SD得三棱锥体积。返回例、已知三棱锥的两个侧面都是边长为 的等边三角
形,另一个侧面是等腰直角三角形。求此三棱锥的体积。
ABCSEF注意:分割法求体积。解法二
提示:设三棱锥S-ABC,侧面SAC、SBC为等边三角形,边长为 ,SA?SB。取SA中点E,AB中点F,连接AE、BE、EF。可证得:SC ?平面ABE。利用:VS-ABC=VS-ABE+VC-ABE
得三棱锥体积。(KEY: )返回例、在棱长为a的正方体ABCD-A1B1C1D1中,求D1到截面C1BD的距离。ABCDA1B1C1D1提示:利用 = 求解。注意:等体积法求点面距离。KEY:返回例:如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
证明:D1E⊥A1D ;
当E为AB的中点时,求点E到面ACD1的距离;
AE等于何值时,二面角D1-EC-D的大小为等体积法求点面距离返回PBCDEA例:已知四棱锥P—ABCD ,PB⊥AD,侧面PAD为边长等于2的正三角形,底面ABCD为菱形,侧面PAD与底面ABCD所成的二面角为120。
(Ⅰ)求点P到平面ABCD的距离;(Ⅱ)求面APB与面CPB所成二面角的大小。等体积法求点面距离通过以上的解答,我们不难看出等体积法在处理点到面的距离和体积时非常有效,因此我们在平时的学习中应该掌握.利用等体积法我们能够从侧面迂回地解决一些从正面较难下手的问题——这是数学中的一种重要思想方法.在利用等体积法时我们应该在原图
形中寻找到一个较容易计算出面积及其高的面来。返回例:正三棱锥的侧面积为18 cm2,高为3cm.被一个过底面中心且平行于一个侧面的平面所截,求这个截面与底面所成的角和面积O解:过底面△ABC的中心O作OD∥BC,交AB、AC于D、E,过DE作平面DEF ∥平面VBC,与平面ABV、平面ACV分别交于DF、EF。设正三棱锥底面边长为 cm,AO与BC交于C,连VG设VG=h cm返回∴ S侧=3× × ×h=18在△VOG中 VG2 =VO2 +OG2
VO = 3
OG = ×解①②得h=2 =6 S截面= × DE×OF
DE= =4
OF= VG=∠AGV= ∠AOF=600返回体积问题: V棱柱=sh V棱锥= shD返回练习:
1.正方体的棱长位 , 以它的上底面中心以及下底面各边中点为顶点的四棱锥的侧面积是_______.
2.已知三棱锥的两个面是边长为 的正三角形,另外两个面是等腰直角三角形,则此三棱锥的体积____________.返回C3.设棱锥的底面面积为8cm2,那么这个棱锥的中截面
(过棱锥的中点且平行于底面的截面)的面积是( )
(A)4cm2 (B) cm2
(C)2cm2 (D) cm2返回4.若一个锥体被平行于底面的平面所截,若截面面积 是底面面积的四分之一,则锥体被截面截得的一个小 锥与原棱锥体积之比为( )
(A)1 : 4 (B) 1 : 3
(C) 1 : 8 (D) 1 : 7 C返回A5.设长方体三条棱长分别为a,b,c,若长方体所有棱的
长度之和为24,一条对角线长度为5 ,体积为2,则
等于( )
(A) (B)
(C) (D)返回C6.斜三棱柱的一个侧面的面积为S,另一条侧棱到这个
侧面的距离是a,则这个三棱柱的体积是( )
(A) (B)
(C) (D)返回A7.在侧棱长为23,每个侧面的顶角均为40°的正三棱锥P-ABC中,过A作截面分别交PB、PC于E、F,则△AEF的最小周长是( )
(A) 6 (B)
(C) 36 (D) 返回8. 如图,在多面体ABCDE中,AE⊥面ABC,BD∥
AE,且AC=AB=BC=BD=2,AE=1,F为CD中点.
(1)求证:EF⊥面BCD;
(2)求多面体ABCDE的体积;
(3)求面CDE与面ABDE所成的二面角的余弦值.【解题回顾】对于不规则几何体一定要能识别其本质,本题的多面体实际上是倒着的四棱锥.返回9.在三棱锥P-ABC中,PA、PB、PC两两成60°角,PA=a,PB=b,PC=c,求三棱锥P-ABC的体积. 【解题回顾】(1)把A、B、C中的任一个点作为顶点(其余三点构成的三角形作为底面)是解题的关键,这说明改变几何体的放置方式或改变对几何体的观察角度在解题中是十分重要的.
(2)当a=b=c时,得到正四面体的体积是?.
(3)若在PA、PB、PC上各任取一点M、N、R,设PM=
m,PN=n,PR=r,则容易证明 ,这一结论与
PA、PB、PC成多大的角无关.返回10.若一个斜棱柱A1B1C1—ABC的底面是等腰△ABC,它的三边边长分别是AB=AC=10cm,BC=12cm,棱柱的顶点A1与A、B、C三点等距,且侧棱AA1=13cm,求此棱柱的全面积.【解题回顾】求斜棱柱全面积的基本方法是求出各个侧面的面积与底面积.本题求侧面积时也可以用直截面BCD的周长去乘AA1而得到.E返回误解分析1.求斜棱柱的全面积,除直截面周长乘侧棱长这个公式外,大多采用逐一求出各表面面积,然后作和的方法,因此不要盲目套什么公式,或在相加时,漏了上、下底面积2.求三棱锥的体积非常灵活,有直接法、割补法、颠倒顶点法等,不管用何种方法,一定要看清字母位置,更不能漏乘1/3.返回与球的多面体问题例.一个凸多面体的棱数为30,面数为12,则它的各面多边形的内角总合是( )(A)5400° (B)6480° (C)7200° (D)7920°提示:运用“欧拉定理” E+2=V+F。返回解:根据欧拉定理 V=(E+2)-F=32-12=20.
设该多面体的12个面的边数分别为E1,E2,……,E12,
那么共有棱数30= ( E1+E2+……+E12),
∴ E1+E2+……+E12=60,
12个面中每个面的内角为
(i=1,2,……,12),
∴ 内角总合为
=6480°,∴ 选B.返回已知凸多面体每个面都是五边形,每个顶点都有三条棱,试求该多面体的面数、顶点数和棱数.返回A1.一个四面体的所有棱长都为√2,四个顶点在同一球面上,则此球的表面积为 ( )
(A) (B) (C) (D)基础题例题2.地球表面上从A地(北纬45°,东经120°)到B地(北纬
45°,东经30°)的最短距离为(地球半径为R) ( )
(A)R (B) (C) (D)C3.在北纬45o的圈上有甲、乙、丙三地,甲乙、乙丙之间
的经度差都是90o,则甲丙两地的球面距离是甲乙两地球
面距离的 ______倍 返回基础题例题C4.球的表面积膨胀为原来的 2 倍,膨胀后的体积为原来的
( )
A. √2倍 B.2倍 C.2√2倍 D.4倍5.棱长为2的正四面体的体积为_____________6.设P、A、B、C是球O面上的四点,且PA、PB、PC两两
互相垂直,若PA=PB=PC=a, 则球心O到截面ABC的距离
是______________返回能力·思维·方法7.求正八面体每相邻两个面所成二面角的大小。ABCFDE解:如图,设棱长为 a,AE中点为F, 连接BF、DF, ∵△ABE,△ADE是正三角形, ∴BF⊥AE,DF⊥AE, ∴∠BFD是二面角B-AE-D的平面角, △BDF中,BF=DE= BD= ∴所求二面角为π- arccos 返回三棱锥A-BCD的两条棱AB=CD=6,其余各棱长均为5,求
三棱锥的内切球半径.E解:取CD的中点E,连接AE,BE,由CD⊥AE,CD⊥BE,得CD⊥平面ABE又AD=5,DE=3,得AE=BE=4,故△ABE的面积为3√7于是,VA-BCD=VC-ABE+VD-ABE显然,三棱锥的三个侧面全等,各侧面的面积为12,设三棱锥的内切球半径为 r,则VA-BCD= (SABC+SBCD+SCDA+SDAB)·r= · 48r =16r 由16r=6√7 得内切球的半径为 返回【解题回顾】
正如三角形的内切圆经常与面积发生关 系一样,多面体的内切球的半径也常与体积发生联系.能力·思维·方法返回例题选讲OO2O1返回能力·思维·方法9.在球内有相距14cm 的两个平行截面,它们的面积分别是
64πcm2 和 36πcm2,求球的表面积。.解:设球半径为R,(1)当截面在球心同侧,如图(1)(1)则有√R2-36-√R2-64=14 而此方程无解,故截面在球心的同侧
不可能。(2)当截面在球心异侧,如图(2)(2)则有√R2-36 +√R2-64=14解得 R=10 ∴S球面=4πR2=400π(cm)2返回返回返回将一个半径为1的球投入底面边长是4的正四棱柱型盛水容器中,求水面上升的高度?返回将一个半径为1的球投入底面边长是4的正四棱柱型盛水容器中,求水面上升的高度?返回求正方体的内切球和它的外接球的表面积之比返回求正四面体的内切球和它的外接球的体积之比HO返回半球的半径为R,一正方体的四个顶点在半球的底面上,另四个顶点在球面上,求正方体的棱长返回例:共端点M的三条线段MA、MB、MC两两垂直,过M、A、B、C刚好可作一个半径为2的球,则MA、MB、MC的平方和为( ) 解:以MA、MB、MC为棱作长方体,那么这个长方体的八个顶点都在球上,且长方体的对角线恰好是球的直径,所以球的直径d=4,
而MA2+MB2+MC2=d2=16.返回延伸·拓展过半径为R的球面上一点作三条两两垂直的弦MA、MB、MC.
(1)求证:MA2+MB2+MC2为定值;
(2)求三棱锥M-ABC的体积的最大值.【解题回顾】(1)MA、MB、MC两两垂直.根据球的对称性,采用补形的方法,可以把它补成一个球的内接长方体.长方体的对角线的平方就是球的直径的平方,即MA2+MB2+MC2=4R2.在做选择题、填充题时就可直接用这个结论.
(2)在球中的线段计算问题,常转化为小圆半径,大圆半径及球心到截面距离来解决. 返回返回误解分析1.在涉及球内接正方体或长方体的题目中,作出的截面一般过多面体的对角线,且对角线长为球的直径?若过对棱中点作横截面,将会出错.2.球面上两点间距离不是直线距离,也不是纬度圈上的劣弧长,而是指过这两点的球大圆上 的劣弧长,不能错啊!返回例:如图所示,在纬度为α的北纬纬线上有一点A,其中α是△AOO’的三内角的等差中项,而t是 与 的等比中项,当地球自转t小时后,求点A转动前后的球面距离.返回解:由题意得 α=60° ,
, t=6,设点A转动后为点B,由于地球转一圈需24小时,因此6小时转了圆周长的 ,
所以∠AO’B=90°, ∠OAO’=30°,所以∠AO’B=90°, ∠OAO’=30°,
所以AO’=Rsin30°= R=BO’, AB= R, 返回返回A1.一个四面体的所有棱长都为2,四个顶点在同一球面上,则此球的表面积为( )
(A) (B) (C) (D)A2.已知一个简单多面体的各个顶点处都有三条棱,则顶点数V与面数F满足的关系式是( )
(A)2F+V=4 (B)2F-V=4
(C)2F+V=2 (D)2F-V=2返回A3.一个凸多面体的顶点数为20,棱数为30.则它的各面多边形的内角总和为( )
(A)2160° (B)5400° (C)6480° (D)7200°A4.将棱长为3的正四面体的各棱长三等分,经过靠近顶点的各分点,将原正四面体各顶点均截去一个棱长为1的小正四面体,剩下的多面体的棱数为( )
(A)16 (B)17 (C)18 (D)19返回A5.地球表面上从A地(北纬45°,东经120°)到B地(北纬
45°,东经30°)的最短距离为(地球半径为R)( )
(A)R (B)
(C) (D)返回翻折问题生活问题 如图,以等腰直角三角形斜边BC上的高AD为折痕,使⊿ ABD和⊿ ACD折成相垂直的两个面。
求证:(1)BD⊥CD;(2)∠ BAC=60°.ABCD返回 例:已知:E、F是正方形ABCD的边BC和CD的中点,分别沿AE、EF、AF将⊿ABE、 ⊿ECF、⊿AFD折起,使B、C、D三点重合于P点,如图所示。
(1)求证:AP ⊥ EF;
(2)?求二面角A-EF-P的大小。
返回解:(1)∵AP⊥PF,AP ⊥PE,
PE∩PE=P
∴ AP⊥平面PEF
又∵EF 平面PEF
∴AP ⊥EF.返回(2)取EF的中点H,连结PH、AH,
∵PE=PF,AE=AF ∴AH ⊥EF,PH ⊥EF
∴ ∠AHP是二面角A-EF-P的平面角。
由(1)知AP ⊥平面PEF,而PH 平面PEF
∴AP ⊥PH,即⊿ APH是Rt⊿.
∴ cos∠AHP= , ∠ AHP=arcos
∴二面角A-EF-P的大小为arcos 。
返回 例:在矩形ABCD中,AB=3,BC=4,沿对角线BD对折成二面角A-BD-C,使A在平面BCD上的射影在BC上。
(1)求异面直线AB与CD所成的角;
(2) 求AB和CD间的距离。
返回 例3:已知Rt⊿ABC中,AB=3,BC=4,E是斜边AC边上的一点,沿BE将ABE折起,使二面角A-BE-C是直二面角,当AC最短时,求∠ABE的大小。
返回练习
1、长方体ABCD-A1B1C1D1中,AB=3,
BC=2,AA1=1,一蚂蚁从点A沿其表面爬
到C1点的最短路程为( )
A、 B、 C、 D、
返回 2、如图代表未折叠正方体的展开图,将其折叠起来,变成正方体后图形是( )
返回5.如图是正方体的平面展开图,在这个正方体中①BM与ED平行;
②CN与BE是异面直线;
③CN与BM成60°的角;
④DM与BN垂直。以上四个命题中,正确
命题的序号是( ) ③ ④返回复习小结
1、解折叠问题首先是准确地画出原来的平面图形及折叠后的空间图形,对照两图形中对应元素的位置、大小、形状,确定不变元素,不变量是解题的基础,折叠所成的二面角往往是解题的关键。返回 2、求侧面上两点间的最短距离,一般都是将空间图形沿某一条棱或母线剪开铺平,化为求两点决定的线段长, 从而化“曲”为“直”,化“折”为“平”。展开是空间问题平面化的一种常用方法。返回一个立方体的六个面上分别标有字母A、B、C、D、F,下图是此立方体的两种不同放置,则与D面相对的面上的字母是 ( )
B返回如图,以长方体ABCD-A1B1C1D1的顶点为顶点且四个面都是直角三角形的四面体是__________
(注:只写出其中的一个,并在图中画出相应的四面体)
返回一间民房的屋顶有如图所示三种不同的盖法:①单向倾斜;②双向倾斜;③四向倾斜.记三种盖法屋顶面积分别为P1、P2、P3.若屋顶斜面与水平面所成的角都是α,则
( )?
(A)P3>P2>P1
(B)P3>P2=P1
(C)P3=P2>P1?
(D)P3=P2=P1?
D返回已知甲烷CH4的分子结构是:中心一个碳原子,外围有4个氢原子(这4个氢原子构成一个正四面体的四个顶点).设中心碳原子到外围4个氢原子连成的四条线段两两组成的角为θ,则cosθ等于 ( )
(A)-1/3 (B)1/3
(C)-1/2 (D)1/2A返回在直角坐标系xoy中,点A、B、C、D的坐标分别为(5,0)、(-3,0)、(0,-4)、(-4,-3),
将坐标平面沿y轴折成直二面角.
(1)求AD、BC所成的角;
(2)BC、OD相交于E,作
EF⊥AD于F,
求证:EF是AD、BC的公垂
线,并求出公垂线段EF的长;
(3)求四面体C-AOD的体积.【解题回顾】这是一道与解几结合的翻折题,画好折后
图将原平面图还原成四棱锥,进一步用三垂线定
理证明AD⊥BC.
返回(1)给出两块相同的正三角形纸片(如图1,图2),要求用其中一块剪拼成一个正三棱锥模型,另一块剪拼成一个正三棱柱模型,使它们的全面积都与原三角形的面积相等,请设计一种剪拼方法,分别用虚线标示在图1、图2中,并作简要说明;
(2)试比较你剪拼的正三棱锥与正三棱柱的体积的大小;
(3)(本小题为附加题)
如果给出的是一块任意三角形的纸片(如图3),要求剪拼成一个直三棱柱模型,使它们的全面积与给出的三角形的面积相等,请设计一种剪拼方法,用虚线标示在图3中,并作简要说明.图1图2返回【解题回顾】本题是2002年高考题,是一道集开放、探索、动手于一体的优秀考题,正三角形剪拼正三棱柱除参考答案的那种剪法外,还可以用如图4的剪法,当然参考答案的剪法是其本质解,因为它为(3)的解答提供了帮助.图1图2图3图4返回5.如图(甲),从三棱锥P-ABC的顶点P沿着三条侧棱PA、PB、PC剪开成平面图形,得到△P1P2P3(如图(乙)),且P1P2=P2P3.(1)在三棱锥P-ABC中,求证:PA⊥BC.
(2)若P1P2=26,P1P3=20,求三棱锥P-ABC的体积.返回综合问题例题讲解1、四棱锥P-ABCD的底面是边长为a的正方形,PB⊥面ABCD.
(1)若面PAD与面ABCD的二面角为600,求四棱锥的体积;作、证、求?∵ PB⊥面ABCD,BA⊥AD, ∴PA⊥AD ∴∠PAB就是面PAD与面ABCD的二面角的平面角解:即∠PAB=600V= a3返回例题讲解1、四棱锥P-ABCD的底面是边长为a的正方形,PB⊥面ABCD.
(2)证明不论高PB怎样变化,面PAD与面PCD所成的二面角恒大于900.M证:由题设侧面PAD与PCD为全等⊿,作CM⊥PD于M,连结MA,则⊿CDM≌⊿ADM,∴AM=CM,∠AMD=900故AMC就是所证二面角的平面角.连结AC在⊿AMC中,由余弦定理
cos∠AMC =故∠AMC>900,即证. 小结:作二面角平面角的方法
●有面的垂线,则一作一连法
●定义法,在两面内作棱的垂线
●面积射影定理返回变化一 四棱锥P-ABCD的底面是边长为a的菱形,∠BCD=600,PB⊥面ABCD.若面PAD与面ABCD的二面角为600,求四棱锥的体积;E返回 四棱锥P-ABCD的底面是边长为a的菱形,∠BCD=600,面PBC⊥面ABCD,且⊿PBC是等边⊿. 求侧面PAD与底面ABCD所成的二面角;变化二E注意:●面面垂直的应用
●分析平面图形返回例题讲解2、如图在直三棱柱ABC-A1B1C1中,底面ABC是等腰Rt⊿, ∠C=900 ,D、E分别是CC1和A1B的中点,AC=AA1=2
(1)求线段DE的长返回例题讲解2、如图在直三棱柱ABC-A1B1C1中,底面ABC是等腰Rt⊿, ∠C=900 ,D、E分别是CC1和A1B的中点,AC=AA1=2
(2)求二面角A-BD-C的大小(反三角表示)解:∵ ABC-A1B1C1是直棱柱,AC⊥BC,∴AC⊥侧面BB1C1C,作CM⊥BD于M,连结AM,则∠AMC就是所求二面角的平面角;在⊿ACM中,AC=2∴tan∠AMC=AC/CM=即所求为AC⊥CM,返回例题讲解3、如图在直三棱柱ABC-A1B1C1中,底面ABC是等腰Rt⊿,∠C=900 ,D、E分别是CC1和A1B的中点,AA1=2,若点E在平面ABD上的射影是⊿ABD的重心G.
(1)求A1B与平面ABD所成的角(用反三角表示);解:连结BG,由已知∠EBG就是所求的角,…… ……∴A1B与平面ABD所成的角为返回例题讲解3、如图在直三棱柱ABC-A1B1C1中,底面ABC是等腰Rt⊿,∠C=900 ,D、E分别是CC1和A1B的中点,AA1=2,若点E在平面ABD上的射影是⊿ABD的重心G.
(2)求点A1到平面AED的距离。方法A:作垂线法方法B:等体积法返回3、如图在直三棱柱ABC-A1B1C1中,底面ABC是等腰Rt⊿,∠C=900 ,D、E分别是CC1和A1B的中点,AA1=2,若点E在平面ABD上的射影是⊿ABD的重心G.
(2)求点A1到平面AED的距离。解A:由上题解知,DE⊥平面AA1B1B∴平面ADE⊥平面AA1B1B于AE在⊿A1AB1中,A1K=方法A:作垂线法返回3、如图在直三棱柱ABC-A1B1C1中,底面ABC是等腰Rt⊿,∠C=900 ,D、E分别是CC1和A1B的中点,AA1=2,若点E在平面ABD上的射影是⊿ABD的重心G.
(2)求点A1到平面AED的距离。解B:方法B:等体积法方法C:对象转换法返回例:如图,已知正三棱柱ABC-A1B1C1中,底面边长为a,侧棱长为 a, D是A1C1上一点.
(1)当 等于多少时,BC1//平面AB1D,
(2)若D是A1C1的中点,
求二面角A1-B1A-D的大小。返回解:(1)如图,连B1C交BC1于E,过E作EF//CA交BA1于F,则EF平行等于 AC,
又AC//A1C1,所以 EF//A1C1.取A1C1的中点D,连DF,则EF//DC1,EF=DC1,所以四边形EFDC1是平行四边形.故 EC1//DF.
又DF 平面AB1D,
EC1 //平面AB1D,
所以BC1//平面AB1D.返回(2)因为D是A1C1的中点,所以B1D⊥平面AA1C1C,所以平面AB1D⊥平面AA1C1C,过A1作A1G⊥AD交AD于G,则A1G⊥平面AB1D.过A1作A1H⊥AB1于H,连HG,则AB1⊥HG,所以∠A1HG是二面角A1-B1A-D的平面角.在Rt△AA1B中.
A1H=返回在Rt△AA1D中,
A1G=在Rt△A1HG中,sin∠A1HG= . 所以∠A1HG=45°, 即二面角A1-B1A-D的大小是45°.返回例:如图所示,在长方体ABCD-A1B1C1D1中,底面A1B1C1D1是正方形,过对角线AC1的一个截面是钝角为α的一个菱形AEC1F,求此截面与底面ABCD所成角φ的大小. 返回在Rt△AEH中,∠AEH= ,AH=HE·tan = a·tan , AC1=2AH= a·tan ,
= EF×AC1=a2tan ,
SABCD=a2, cosφ=
∴ φ=arccos(cot ).解:∠AEC1=α,设正方形AC1边长为a,则BD= a,且EF//BD,EF= a,EF⊥AC1,返回例:如图,在直三棱柱ABC-A1B1C1中,AB1⊥BC1,AB=CC1=a,BC=b,
(1)设E、F分别是AB1、BC1的
中点,求证:EF//平面ABC;
(2)求证:A1C1⊥AB;
(3)求B1到平面ABC1的距离. 返回(1)设E、F分别是AB1、BC1的中点,求证:EF//平面ABC;解:(1)分别取AB、BC的中点M、N,连EM、MN、NP,于是EM BB1,FN BB1,
从而EM FN,即四边形EFNM是平行四边形,
∴ EF//MN,而EF 平面ABC, MN 平面ABC,
∴ EF//平面ABC;返回(2)求证:A1C1⊥AB;(2)连A1B,∵ ABC-A1B1C1是直三棱柱,∴ AA1⊥AB,
又AB=CC1=AA1,∴ ABB1A1是正方形,从而AB1⊥BA1,
∵ AB1⊥BC1,∴ AB1⊥平面A1BC1,∴ A1C1⊥AB1,
而A1C1⊥AA1,∴ A1C1⊥平面ABB1A1,∴ A1C1⊥AB; 返回(3)求B1到平面ABC1的距离. (3)∵ A1B1//AB,∴ A1B1//平面ABC, 于是B1到平面ABC1的距离等于A1到平面ABC1的距离,
自A1作A1H⊥AC1于H,由(2)知 BA⊥平面ACC1A1, ∴ BA⊥A1H,于是A1H⊥平面ABC1,
在Rt△AA1C1中,AA1=CC1=a,返回此即B1到平面ABC1的距离。 返回在棱长为a的正方体ABCD-A1B1C1D1中,E、F分别是棱AB与BC的中点,(1)求二面角B-FB1-E的大小;(2)求点D到平面B1EF的距离;(3)在棱DD1上能否找一点M,使BM⊥平面EFB.若能,试确定点M的位置,若不能,请说明理由.【解题回顾】此题也可以作面B1EF的垂线与DD1相交,再
说明可以找到一点M满足条件.过程如下:先证明面B1BDD1
⊥面B1EF,且面B1BDD1∩面B1EF=B1G,在平面B1BDD1内作BM
⊥B1G,延长交直线DD1于M,由二平面垂直的性质可得:
BM⊥面B1EF,再通过△B1BG∽△BDM可得M是DD1的中点,
∴在棱上能找到一点M满足条件.
此题是一道探索性命题.往往可先通过对条件的分析,猜
想出命题的结论,然后再进行证明.返回M返回练习题BC返回返回返回返回返回(05,浙江)、如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
(Ⅰ)当k= 时,求直线PA与平面PBC所成角的大小
(Ⅱ) 当k取何值时,O在平面PBC内的射影恰好为△PBC的重心?返回 三棱锥P-ABC中,侧面PAC与底面ABC
垂直,PA=PB=PC=3,
(1)求证:AB ⊥ BC;
(2)设AB=BC= ,求AC与平面PBC所成
角的大小. (2004年全国文科试题)EF返回(Ⅰ)证明:面PAD⊥面PCD;
(Ⅱ)求AC与PB所成的角;
(Ⅲ)求面AMC与面BMC
所成二面角的大小。例1.(05,全国,18)已知四棱锥P-ABCD的底面为直角梯形,AB∥DC, 底面ABCD,且PA=AD=DC= AB=1,M是PB的中点。返回例3、如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
(Ⅰ)求证:AE⊥平面BCE;
(Ⅱ)求二面角B-AC-E的大小;
(Ⅲ)求点D到平面ACE的距离。返回如图,在四棱锥P—ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB= ,BC=1,PA=2,E为PD的中点.
(Ⅰ)求直线AC与PB所成角的余弦值;
(Ⅱ)在侧面PAB内找一点N,使NE⊥面PAC,并求出N点到AB和AP的距离.返回思想方法: 空间的距离主要指点面距、线面距和面面距,
而后两种的求解一般可转化为第一种,即线面距
及面面距都是通过转化最终转为求解点面距解决
而完成的。(转化的思想)
例如:
平行问题垂直问题角度问题距离问题柱锥问题体积面积问题多面体与球的问题生活问题和翻折问题综合问题立几概念和方法动态的立体几何正方体的截面问题三棱柱的体积分割平行问题返回直线和平面的位置关系直线和平面的平行关系平面和平面的平行关系返回直线在平面内直线和平面相交直线和平面平行线面位置关系有无数个公共点有且仅有一个公共点没有公共点返回平行于同一平面的二直线的位置关系是 ( )(A) 一定平行(B) 平行或相交(C) 相交(D) 平行,相交,异面D返回(1)点A是平面?外的一点,过A和平面?平行的直线有 条。α无数返回(2)点A是直线l 外的一点,过A和直线l 平行的平面有 个。无数返回(3)过两条平行线中的一条和另一条平行的平面有 个。无数返回(4)过两条异面直线中的一条和另一条平行的平面有 个。且仅有一返回(5)如果l1 // l2 , l1 平行于平面?,则l2 平面?l1?? 或 //返回(6)如果两直线a,b相交,a平行于平面?,则b与平面?的位置关系是 。a?相交或平行返回过直线L外两点,作与直线L平行的平面,这样的平面( )(A) 有无数个(C) 只能作出一个(B) 不能作出(D) 以上都有可能情况一返回(A) 有无数个(C) 只能作出一个(B) 不能作出(D) 以上都有可能过直线L外两点,作与直线L平行的平面,这样的平面( )情况二返回过直线L外两点,作与直线L平行的平面,这样的平面( )(A) 有无数个(C) 只能作出一个(B) 不能作出(D) 以上都有可能D情况三返回例: 有以下四个命题:
① 若一条直线与另一条直线平行,则它就与经过另一条直线的平面平行;
② 若一条直线垂直于一个平面的一条垂线,则此直线平行于这个平面;
③ 若一条直线和一个平面内的两条直线都垂直,则此直线必垂直于这个平面;
④ 平面内两条平行直线,若其中一条直线与一个平面平行,则另一条直线也与这个平面平行. 其中正确命题的个数是( ).
A.0 B.1 C.2 D.3返回解:① 不正确,若一条直线与另一条直线平行,则这条直线可能与经过另一条直线的平面平行,也可能在平面内;
② 不正确,与①相仿,若一条直线垂直于一个平面的一条垂线,则此直线可能平行于这个平面,也可能在平面内;返回 ③ 不正确,若一条直线和一个平面内的两条直线都垂直,如果在平面内的两条直线平行,则无法判断直线是否垂直于这个平面;
④ 不正确,与①②相仿,该直线仍有可能在平面内。
所以四个命题都是错误的,选A。返回线面平行的判定(1)定义——直线与平面没有公共点(2)定理——如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。返回线面平行判定定理——如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。已知:a??? b??? a//b求证:a//?ab?(1) a,b确定平面?,???=b(2) 假设a与?不平行则a与?有公共点P则P? ???=b(3) 这与已知a//b矛盾(4) ∴a // ??返回 如图,空间四面体P-ABC,M,N分别是面PCA和面PBC的重心,求证:MN//面BCAP∵MN// EF∴ MN //面BCA线线平行线面平行返回如图,两个全等的正方形ABCD和ABEF所在平面交于AB,M.N分别是对角线上的点,AM=FN。求证:MN//面BCE。ABCDEFMN∵MN // GH∴ MN //面BCE线线平行线面平行返回ABCDEFMN∵△AFN∽ △BNH∴ AN/NH=FN/BN∴ AN/NH=AM/MC∴ MN//CH∴ MN //面BCE如图,两个全等的正方形ABCD和ABEF所在平面交于AB, M.N分别是对角线上的点,AM=FN,求证:MN//面BCE。返回 在正方体AC1中,E为DD1的中点,求证:DB1//面A1C1EE∵DB1 // EF∴ DB1 //面A1C1E线线平行线面平行返回在正方体AC1中,O为平面ADD1A1的中心,求证:CO // 面A1C1BB1O返回(1)如果一条直线与一个平面平行,则这条直线与这个平面无公共点(2)如果一条直线与一个平面平行,则这条直线与这个平面内的直线成异面直线或平行直线(3)如果一条直线与一个平面平行,经过这条直线的平面和这个平面相交,则这条直线与交线平行。返回已知:a//?,a??, ? ? ?=b求证:a//b? ? ?=bb ? ?a //?a ? b=?a//b返回如果平面外的两条平行线中的一条与这个平面平行,则另一条直线与这个平面也平行abc返回如果一条直线和两个相交平面都平行,则这条直线与它们的交线平行a??l已知:a // ?, a// ? ,? ? ?=l求证:a // l返回abABOMNP如图,a,b是异面直线,O为AB的中点,过点O作平面?与两异面直线a,b都平行MN交平面于点P,求证:MP=PN?返回一、两个平面平行的判定方法1、两个平面没有公共点2、一个平面内有两条相交直线都平行于另一个平面3、都垂直于同一条直线的两个平面两个平面平行返回二、两个平面平行的性质4、一直线垂直于两个平行平面中的一个,则它也垂直于另一个平面2、其中一个平面内的直线平行于另一个平面3、两个平行平面同时和第三个平面相交,它们的交线平行两个平面平行5、夹在两个平行平面间的平行线段相等1、两个平面没有公共点返回判断下列命题是否正确?1、平行于同一直线的两平面平行2、垂直于同一直线的两平面平行3、与同一直线成等角的两平面平行返回4.垂直于同一平面的两平面平行5.若α∥β,则平面α内任一直线a ∥β返回2. 如图,设AB、CD为夹在两个平行平面 、 之间
的线段,且直线AB、CD为异面直线,M、P 分别为AB、CD 的中点,
求证: 直线MP // 平面 .返回例:如图,在正方体ABCD-A1B1C1D1 中,求证:面AB1D1∥面BDC1证明:B1D1∩AB1=B1面AB1D1∥
面BDC1线∥线线∥面面∥面返回证法2:A1C⊥BDBD∩BC1=BA1C⊥面BDC1面AB1D1
∥面BDC1返回变形1:如图,在正方体ABCD-A1B1C1D1中,E,F,G分别为A1D1,A1B1,A1A的中点,求证:面EFG∥面BDC1变形2:若O为BD上的点
求证:OC1 ∥面EFG
O面∥面 由上知面EFG∥面BDC1线∥面OC1 ∥面EFG证明:返回变形3:如图,在正方体ABCD-A1B1C1D1 中,E,F,M,N分别为A1B1,A1D1, B1C1, C1D1 的中点求证:面AEF∥面BDMN返回小结:线
平行
线 线
平行
面 面
平行
面线面平行判定线面平行性质面面平行判定面面平行性质三种平行关系的转化返回 已知:四面体A-BCD,E,F,G分别为AB,AC,AD的中点.求证:面EFG∥面BCD练习返回垂直问题线面垂直的判定方法(1)定义——如果一条直线和一个平面内的任意一条直线都垂直,则直线与平面垂直。(2)判定定理1——如果两条平行线中的一条垂直于一个平面,则另一条也垂直于这个平面。(3)判定定理2——如果一条直线和一个平面内的两条相交直线都垂直,则直线与平面垂直。返回线面垂直的性质(1)定义——如果一条直线和一个平面垂直则这条直线垂直于平面内的任意一条直线(2)性质定理——如果两条直线同垂直于一个平面,则这两条直线平行。返回填空(1)l ?? , m?? ? l____m(2) n??, m?? , m与n_____, l ?m, l ?n, ? l ?? (3)l ?? , m ?? , ? l____m(4)l //m , l ?? , ? m____ ?相交?//?返回PABC?如图,AB是圆O的直径,C是异于A,B的圆周上的任意一点,PA垂直于圆O所在的平面(1)BC⊥面PAC返回PABC?2)若AH⊥PC,则AH⊥面PBC如图,AB是圆O的直径,C是异于A,B的圆周上的任意一点,PA垂直于圆O所在的平面返回O在正方体AC1中,O为下底面的中心,求证:AC⊥面D1B1BD返回OH在正方体AC1中,O为下底面的中心,B1H ⊥D1O,求证:B1H⊥面D1AC返回已知: l // ? ,m? ?求证: l ? m m?返回返回如果一个平面经过另一个平面的一条垂线,则这两个平面互相垂直返回如图,C为以AB为直径的圆周上一点, PA⊥面ABC,找出图中互相垂直的平面。∵PA⊥面ABC∴面PAC⊥面ABC∴面PAB⊥面ABC∵BC⊥面PAC∴面PBC⊥面PAC返回如果两个平面垂直,则在一个平面内垂直于它们的交线的直线垂直于另一个平面返回求证:如果一个平面与另一个平面的垂线平行,则这两个平面互相垂直??返回求证:如果两个相交平面都与另一个平面垂直,则这两个平面的交线 l 垂直于另一个平面???l返回求证:如果两个相交平面都与另一个平面垂直,则这两个平面的交线 l 垂直于另一个平面???l返回四面体ABCD中,面ADC⊥面BCD,面ABD ⊥面BCD,设DE是BC边上的高, 求证: 平面ADE ⊥面ABC 面ADC⊥面BCD面ABD ⊥面BCDAD ⊥面BCDAD ⊥BCDE ⊥BCBC ⊥面ADE面ABC ⊥面ADE①②③④返回⊿ABC是直角三角形, ∠ACB=90°,P为平面外一点,且PA=PB=PC . 求证: 平面PAB ⊥面ABC 返回课堂练习课堂练习空间四面体ABCD中,若AB=BC,AD=CD,E为AC的中点,则有( )(A) 平面ABD ⊥面BCD(B) 平面BCD ⊥面ABC(C) 平面ACD ⊥面ABC(D) 平面ACD ⊥面BDE返回如图,ABCD是正方形,PA ⊥面ABCD,连接PB,PC,PD,AC,BD,问图中有几对互相垂直的平面?面PAC⊥面ABCD面PAB⊥面ABCD面PAD⊥面ABCD面PAD⊥面PAB面PAD⊥面PCD面PBC⊥面PAB面PBD⊥面PAC返回如图,三棱锥P-ABC中,PB⊥底面ABC,∠ACB= 90°,PB=BC=CA,E为PC中点,返回如图,四棱锥P-ABCD的底面是菱形,PA⊥底面ABCD,∠BAD= 120°,E为PC上任意一点,返回例:如图,在四面体SABC中,∠ASC=90°,∠ASB=∠BSC=60°,SA=SB=SC,
求证:平面ASC⊥平面ABC。返回 证明:容易证得AB=BC=SB,取AC中点D,连SD、BD,得SD⊥AC,BD⊥AC,
由∠ASC=90°,设SA=SB=SC=a,
解得SD= a,BD= a,
而SB=a, ∴ ∠SDB=90°,
∴平面ASC⊥平面ABC。返回角度问题一、概念直线a、b是异面直线,经过空间任意一点o,作直线a’、b’,并使a’//a,b’//b,我们把直线a’和b’所成的锐角(或直角)叫做异面直线a和b所成的角。返回aαbO是空间中的任意一点 点o常取在两条异面直线中的一条上θooooo返回一、概念直线a、b是异面直线,经过空间任意一点o,作直线a’、b’,并使a’//a,b’//b,我们把直线a’和b’所成的锐角(或直角)叫做异面直线a和b所成的角。返回θαBA返回一、概念直线a、b是异面直线,经过空间任意一点o,作直线a’、b’,并使a’//a,b’//b,我们把直线a’和b’所成的锐角(或直角)叫做异面直线a和b所成的角。从一条直线出发的两个半平面所组成的图形叫做二面角。以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角。返回ABO返回一、概念直线a、b是异面直线,经过空间任意一点o,作直线a’、b’,并使a’//a,b’//b,我们把直线a’和b’所成的锐角(或直角)叫做异面直线a和b所成的角。从一条直线出发的两个半平面所组成的图形叫做二面角。以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角。AαβLBO返回二、数学思想、方法、步骤: 解决空间角的问题涉及的数学思想主要是化归与转化,即把空间的角转化为平面的角,进而转化为三角形的内角,然后通过解三角形求得。2.方法:3.步骤:b.求直线与平面所成的角:a.求异面直线所成的角:c.求二面角的大小:①作(找)② 证③ 点④ 算1.数学思想:返回在正方体AC1中,求异面直线A1B和B1C所成的角?A1B和B1C所成的角为60°和A1B成角为60°的面对角线共有 条。返回在正方体AC1中,求异面直线D1B和B1C所成的角?ABDCA1B1D1C1返回在正方体AC1中,M,N分别是A1A和B1B的中点,求异面直线CM和D1N所成的角?MN返回PABCMN空间四边形P-ABC中,M,N分别是PB,AC的中点,PA=BC=4,MN=3,求PA与BC所成的角?返回1. 在正方体AC1中,E、G分别是AA1和
CC1的中点, F在AB上,且C1E⊥EF,
则EF与GD所成的角的大小为( )
(A) 30° (B) 45° (C) 60°(D) 90°DM EB1是EC1在平面AB1
内的射影EB1 ⊥EF
DG∥AM∥EB1
EF ⊥DG返回已知:两异面直线a,b所成的角是50 °,P为
空间中一定点,则过点P且与a,b都成30°角的
直线有 条。abPO2返回A1ABB1CDC1D1FE解:如图,取AB的中点G ,O(证)(点)(算)(作)例1:如图,在正方体ABCD-A1B1C1D1中,E、F分别是BB1 、CD中点。求AE与D1F所成的角。返回例2、长方体ABCD-A' B'C' D'中, AB=BC=4, AA' =6, E、F分别为BB' 、CC'的中点, 求AE、BF所成角的余弦值.返回例3:长方体ABCD-A1B1C1D1,AB=AA1=2 cm, AD=1cm,求异面直线A1C1与BD1所成角的余弦值。返回取BB1的中点M,连O1M,则O1M??D1B,如图,连B1D1与A1C1 交于O1,于是?A1O1M就是异面直线A1C1与BD1所成的角(或其补角)O1M解:为什么?返回解法二:方法归纳:补形法把空间图形补成熟悉的或完整的几何体,如正方体、长方体等,其目的在于易于发现两条异面直线的关系。 返回解法二:方法归纳:补形法把空间图形补成熟悉的或完整的几何体,如正方体、长方体等,其目的在于易于发现两条异面直线的关系。 在?A1C1E中,由余弦定理得?A1C1与BD1所成角的余弦值为 如图,补一个与原长方体全等的并与原长方体有公共面连结A1E,C1E,则?A1C1E为A1C1与BD1所成的角(或补角),BC1的长方体B1F,返回例: 如图,在正方体 ABCD-A1B1C1D1中,异面直线AC与BC1所成角的大小是( ).
A.30° B.45° C.60° D.90°返回例: 如图,正三棱锥S-A BC的侧棱与底面边长相等,如果E、F分别为SC、 A B的中点,那么异面直线EF与SA所成角等于( ) A.90° B.60° C.45° D.30°返回解:取AC的中点G,连接EG、FG,
∵ EG//SA,∴ ∠GEF是异面直线EF与SA所成角,又FG//BC,SA⊥BC,
∴ ∠EGF=90°,
△EGF是直角三角形,又EG=SA,FG=BC,
∴ EG=FG,△EGF是等腰直角三角形,
∴ ∠GEF=45°,选C.返回
正方体ABCD- A1B1C1D1中,AC、BD交于O,则OB1与A1C1所成的角的度数为练习1900返回在正四面体S-ABC中,SA⊥BC, E, F分别为SC、AB 的中点,那么异面直线EF 与SA 所成的角等于( )CD(A)300 (B)450 (C)600 (D)900练习2B返回例:已知正方体的棱长为 a , M 为 AB 的中点, N 为 BB1的中点,求 A1M 与 C1 N 所成角的余弦值。解:EG如图,取AB的中点E, 连BE, 有BE∥ A1M 取CC1的中点G,连BG. 有BG∥ C1N 则∠EBG即为所求角。BG=BE= a, F C1 = a由余弦定理,cos∠EBG=2/5F取EB1的中点F,连NF,有BE∥NF则∠FNC为所求角。想一想:还有其它定角的方法吗?在△EBG中返回定角一般方法有:(1)平移法(常用方法)小结:1、求异面直线所成的角是把空间角转化为平面 角,体现了化归的数学思想。2、用余弦定理求异面直线所成角时,要注意角的 范围: (1) 当 cosθ > 0 时,所成角为 θ(2) 当 cosθ < 0 时,所成角为π- θ(3) 当 cosθ = 0 时,所成角为 3、当异面直线垂直时,还可应用线面垂直的有 关知识解决。90o(2)补形法化归的一般步骤是:定角求角返回说明:异面直线所成角的范围是(0, ],在把异面直线所成的角平移转化为平面三角形中的角,常用余弦定理求其大小,当余弦值为负值时,其对应角为钝角,这不符合两条异面直线所成角的定义,故其补角为所求的角,这一点要注意。 返回斜线与平面所成的角平面的一条斜线和它在这个平面内的射影所成的锐角返回若斜线段AB的长度是它在平面?内的射影长的2倍,则AB与?所成的角为 。60°返回最小角原理C斜线与平面所成的角,是这条斜线和这个平面内的直线所成的一切角中最小的角。返回若直线 l1与平面所成的角为60 ° ,则这条直线与平面内的直线所成的一切角中最小的角 ,最大的角为 。90°60°Ol1返回若直线 l1与平面所成的角为30 ° ,直线 l2 与 l1 所成的角为60 °,求直线 l2与平面所成的角 的范围?l1返回如图,直线OA与平面?所成的角为?,平面内一条直线OC与OA的射影OB所成的角为,设∠AOC为?2求证:cos?2= cos ?1 ×cos ?返回求直线与平面所成的角时,应注意的问题:(1)先判断直线与平面的位置关系(2)当直线与平面斜交时,常采用以下步骤:①作出或找出斜线上的点到平面的垂线②作出或找出斜线在平面上的射影③求出斜线段,射影,垂线段的长度④解此直角三角形,求出所成角的相应函数值返回例题:如图,在正方体ABCD-A1B1C1D1中,求A1B与平面A1B1CD所成的角O返回SACBOFE如图,?ACB=90?,S为平面ABC外一点, ?SCA= ?SCB= 60?,求SC与平面ACB所成的角.返回SACBOFE如图,SA,SB,SC是三条射线,?BSC=60?,SA上一点P到平面BSC的距离是3, P到SB,SC的距离是5,求SA与平面BSC所成的角P返回ABCDFEADFD’A’CA1BE正方形ABCD边长为3,AE=2BE,CF=2DF,沿EF将直角梯形AEFD折起,使点A’的射影点G落在边BC上,求A’E与平面ABCD所成的角?返回如图,在正方体ABCD-A1B1C1D1中,O为下底面AC的中心,求A1O与平面BB1D1D所成的角.OO`返回正四面体P—ABC中,求侧棱PA与
底面ABC所成的角PABCD返回从一条直线出发的两个半平面所形成的图形叫做二面角这条直线叫做二面角的棱从一条直线出发的两个半平面所形成的图形叫做二面角这条直线叫做二面角的棱返回以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角返回基础题例题1.下列命题中:
①两个相交平面组成的图形叫做二面角;
②异面直线a、b分别和一个二面角的两个面垂直,则a、b组成的角与这个二面角的平面角相等或互补;
③二面角的平面角是从棱上一点出发,分别在两个面内作射线所成角的最小角;
④正四面体相邻两个面所成的二面角的平面角是锐角.
其中,正确命题的序号是______________.②、④返回2.如图,正方体ABCD—A1B1C1D1中,二面角B1-AA1-C1的大小为_____,二面角B-AA1-D的大小为______,二面角C1-BD-C的正切值是_______.45°90°基础题例题返回3. 在二面角α-l-β的一个平面α内有一条直线AB,它 与棱 l 所成的角为45°,与平面β所成的角为30°,则 这个二面角的大小是________________.45°或135°基础题例题返回B4. 在二面角α-a-β内,过a作一个半平面γ,使二面角 α-a-γ为45°,二面角γ-a-β为30°,则γ内的任意
一 点P到平面α与平面β的距离之比为( )
(A) (B)
(C) (D)基础题例题返回基础题例题5. PA、PB、PC是从P点引出的三条射线,每两条的夹角
都是60o,则二面角B –PA—C的余弦值是 ( )
A. B. C. D.AD返回ABCA′M已知:如图⊿ABC的顶点A在平面M上的射影为点A′, ⊿ABC的面积是S, ⊿A′BC的面积是S′,设二面角A-BC-A′为?.求证:COS ? = S ′÷ S返回在正方体AC1中,求二面角D1-AC-D的大小?返回 过正方形ABCD的顶点A引SA⊥底面ABCD,并使平面SBC,SCD都与底面ABCD成45度角,求二面角B-SC-D的大小.E返回7.已知斜三棱柱ABC—A1B1C1中,∠BCA=90°,AC=
BC,A1在底面ABC的射影恰为AC的中点M. 又知AA1
与底面ABC所成的角为60°.
(1)求证:BC⊥平面AA1C1C;
(2)求二面角B-AA1-C的大小.能力·思维·方法返回7.已知斜三棱柱ABC—A1B1C1中,∠BCA=90°,AC=BC,A1在底面ABC的射影恰为AC的中点M. 又知AA1与底面ABC所成的角为60.(1)求证:BC⊥平面AA1C1C;(2)求二面角
B-AA1-C的大小.能力·思维·方法证明: (1)由题设知,A1M⊥平面ABC,又A1M 平面AA1C1C,∴(1)平面AA1C1C⊥底面ABC,又BC⊥AC,平面AA1C1C∩平面ABC=AC,∴BC ⊥平面AA1C1C返回7.已知斜三棱柱ABC—A1B1C1中,∠BCA=90°,AC=BC,A1在底面ABC的射影恰为AC的中点M. 又知AA1与底面ABC所成的角为60.(1)求证:BC⊥平面AA1C1C;(2)求二面角
B-AA1-C的大小.能力·思维·方法证明: (2)由题设知,A1M⊥平面ABC,∴AA1与底面ABC所成角为∠A1AC,∴∠A1AC=60o,又M是AC中点,∴△AA1C是正三角形,作CN⊥AA1于N,∴点N是AA1的中点,连接BN,由BC ⊥平面AA1C1C,∴BC⊥AA1,∴作AA1 ⊥平面BNC,∴AA1 ⊥BN ,∴∠BNC是二面角B--AA1—C的平面角,返回7.已知斜三棱柱ABC—A1B1C1中,∠BCA=90°,AC=BC,A1在底面ABC的射影恰为AC的中点M. 又知AA1与底面ABC所成的角为60.(1)求证:BC⊥平面AA1C1C;(2)求二面角
B-AA1-C的大小.能力·思维·方法设AC=BC=a,正三角形AA1C的边长为a,∴在直角三角形BNC中,∴二面角B—AA1—C的大小是返回【解题回顾】①先由第(1)小题的结论易知BC⊥AA1,
再利用作出棱AA1的垂面BNC来确定平面角∠BNC.
②将题设中“AA1与底面ABC所成的角为60°”改为 “ BA1⊥AC1 ” 仍可证得三角形AA1C为正三角形,所求 二面角仍为 .
③本题的解答也可利用三垂线定理来推理.能力·思维·方法返回在正方体AC1中,E,F分别是AB,AD的中点,求二面角C1-EF-C的大小?EFABDCA1B1D1C1H返回⊿ABC中,AB⊥BC,SA ⊥平面ABC,DE垂直平分SC,又SA=AB,SB=BC,求二面角E-BD-C的大小?SABCED返回求正四面体的侧面与底面所成的二面角的大小?E返回三棱锥P-ABC中,PA ⊥平面ABC,PA=3,AC=4,PB=PC=BC. (1)求二面角P-BC-A的大小34H返回 (2)求二面角A-PC-B的大小COS ?=三棱锥P-ABC中,PA ⊥平面ABC,PA=3,AC=4,PB=PC=BC. (1)求二面角P-BC-A的大小返回在正方体AC1中,E,F分别是中点,求截面A1ECF和底面ABCD所成的锐二面角的大小.EF返回EF在正方体AC1中,E,F分别是中点,求截面A1ECF和底面ABCD所成的锐二面角的大小.返回例: 如图ABC-A1B1C1是各条棱长均为2的正三棱柱, (1)求 AB1与A1C所成角?(2)求AB1与平面BB1C1C所成角?(3) 若点D是侧棱CC1的中点,求平面AB1D与平面ABC所成角?
A1AB1C1BC返回例: 如图ABC-A1B1C1是各条棱长均为2的正三棱柱, (1)求 AB1与A1C所成角?返回解: 分别取A1A,AC, A1B1的中点N,M, G,连接GN,NM.则∠GNM为所求角.并连接GM.GM每条棱长为2GM= 所求角大小为:arccosN返回1. 如图ABC-A1B1C1是各条棱长均为2的正三棱柱, (1)求 AB1与A1C所成角?(2)求AB1与平面BB1C1C所成角?E所求角大小为:arcsin返回例: 如图ABC-A1B1C1是各条棱长均为2的正三棱柱,(3) 若点D是侧棱CC1的中点,求平面AB1D与平面ABC所成角?A1AB1C1BCD返回则:AG所求角大小为:返回A1AB1C1BCDM ∠B1AB为二面角B1-AM-B的平面角.返回 解:延长B1D交BC延长线于M,连接AMCM=CB=CA所求角大小为:点D是CC1的中点,且CD//BB1返回CABDA1B1C1D1MN返回CABDA1B1C1D1MN返回CABDA1B1C1D1MN返回CABDA1B1C1D1MN返回CABDA1B1C1D1MN返回CABDA1B1C1D1MN返回返回B1A1C1 ABC例: 在直三棱柱ABC-A1 B1 C1中, ∠ BAC=90o,AB=BB1=1,直线B1C与平面ABC成30o 的角,
求二面角B-B1C - A的余弦值。分析:求二面角B- B1C-A的度数,要作出平面角,显然二面
角的棱为B1C,故需在B1C上取一点,然后分别在两个面内作垂
直于棱的两条射线。返回C1 AA1B1BC返回1.熟练掌握求二面角大小的基本方法:(1)先作平面角,再求其大小;
(2)直接用公式2.掌握下列两类题型的解法:(1)折叠问题——将平面图形翻折成空间图形.(2)“无棱”二面角——在已知图形中未给出二面角的棱.返回基础题例题二面角α-AB-β的平面角是锐角,C是平面α内的
点(不在棱AB上),D是C在平面β上的射影,E是棱
AB上满足∠CEB为锐角的任意一点,则( )
(A)∠CEB>∠DEB (B)∠CEB=∠DEB
(C)∠CEB<∠DEB
(D)∠CEB与∠DEB的大小关系不能确定A返回2. 直线AB与直二面角α-l-β的两个半平面分别交于A、B两点,且A、B l. 如果直线AB与α、β所成的角 分别是θ1、θ2,则θ1+θ2的取值范围是( )
(A)
(B)
(C)
(D)D基础题例题返回在长、宽、高分别为1、1、2的长方体ABCD-A1B1
C1D1中,截面BA1C1与底面ABCD所成角的余弦值是__
_____.4. 把边长为a的正三角形ABC沿着过重心G且与BC平 行的直线折成二面角,此时A点变为 ,当
时,则此二面角的大小为__________________.arccos(1/3)基础题例题返回5.已知正方形ABCD中,AC、BD相交于O点,若将正方
形ABCD沿对角线BD折成60°的二面角后,给出下面4个
结论:
①AC⊥BD;②AD⊥CO;③△AOC为正三角形;
④过B点作直线l⊥平面BCD,则直线l∥平面AOC,
其中正确命题的序号是________①③④基础题例题返回6. 在四面体P—ABC中,PC⊥平面ABC,
AB=BC=CA=PC,求二面角B—AP—C的大小. EF解:如图过B作BE⊥AC于E,过E作EF⊥PA于F,连结BF。
∵PC⊥平面ABC,∴BE⊥平面PAC,∴BF⊥PA。
∴∠BFE就是二面角B―PA―C的平面角。设PC=1 则AB=BC=CA=PC=1,
∴E为AC的中点,∴所求二面角大小为: 能力·思维·方法………………返回能力·思维·方法7.平面四边形ABCD中,AB=BC=CD=a,∠B=90°,∠DCB=135°,沿对角线AC将四边形折成直二面角.
证:(1)AB⊥面BCD;(2)求面ABD与面ACD所成的角.返回能力·思维·方法7.平面四边形ABCD中,AB=BC=CD=a,∠B=90°,∠DCB=135°,沿对角线AC将四边形折成直二面角.
证:(1)AB⊥面BCD;(2)求面ABD与面ACD所成的角.证明: (1)D-AC-B是直二面角,又∵DC⊥AC,∴DC⊥平面ABC,(面面垂直性质定理)又AB 平面ABC,∴DC⊥AB,又AB⊥BC,∴AB⊥平面BCDABCD返回能力·思维·方法7.平面四边形ABCD中,AB=BC=CD=a,∠B=90°,∠DCB=135°,沿对角线AC将四边形折成直二面角.
证:(1)AB⊥面BCD;(2)求面ABD与面ACD所成的角.证明: (2)过C作CH⊥DB于H,∴平面ABD⊥平面DCB,∴CH⊥平面ABD,∵AB⊥平面BCD又∵平面ABD ∩平面DCB=DB,BH过H作HE⊥AD于E,E连接CE,由三垂线定理知 CE⊥ADHE⊥ADCE⊥AD∴∠CEH是所求二面角
的平面角,∴∠CEH=60o,即所求二面角为 60o返回【解题回顾】准确画出折叠后的图形,弄清有关点、 线之间的位置关系,便可知这是一个常见空间图形 (四个面都是直角三角形的四面体).能力·思维·方法返回例.A为二面角α-l-β的棱l上一点,射线AB α,且与棱成45°角,与β成30°角,则二面角α-l-β的大小是( )。(A)45° (B)30° (C)45°或135° (D)30°或150°提示:分锐二面角和钝二面角两种情况讨论返回∴sin∠BCD=
∴ ∠BCD=45°,返回如图(2),若二面角α-l-β是钝二面角,自B作BD⊥β,D为垂足,作BC⊥l于C,C为垂足,连接CD,延长DC到E,则由三垂线定理得CE⊥l,∴ ∠BCE是二面角α-l-β的平面角,而∠BCD是二面角α-l-β的平面角的补角,由(1)解得∠BCD=45°,
∴ ∠BCE=135°,
即二面角的大小是45°或135°,选C. 返回8.在直角梯形P1DCB中,P1D∥CB,CD⊥P1D,P1D=
6,BC=3,DC=3,A是P1D的中点. 沿AB把平面P1AB折起到平面PAB的位置,使二面角P-CD-B成45°,设E、F分别为AB、PD的中点.
(1)求证:AF∥平面PEC;
(2)求二面角P-BC-A的大小;能力·思维·方法EFP..证明:(1)取PC的中点G,.G连接FG、EG,则FG//CD,且FG= CD,∵AE//CD,且AE= CD∴AE//FG,AE=FG,从而四边形AEGF是平行四边形,∴AF//EG,EG 平面PEC,∴AF//平面PEC返回8.在直角梯形P1DCB中,P1D∥CB,CD⊥P1D,P1D=
6,BC=3,DC=3,A是P1D的中点. 沿AB把平面P1AB折起到平面PAB的位置,使二面角P-CD-B成45°,设E、F分别为AB、PD的中点.
(1)求证:AF∥平面PEC;
(2)求二面角P-BC-A的大小;能力·思维·方法P证明:(2)∵CD⊥平面PAD,∴平面PAD⊥平面ABCD∴∠PAB为二面角P-BC-A的平面角,在Rt△PAB中,PA=3,PB= ,∵PA=AD,且∠PDA=45o,∴PA⊥AD∴PA⊥平面ABCD,∴AB⊥BC由三垂线定理得 PB⊥BC∴sin∠PBA=得所求的二面角为60o返回【解题回顾】找二面角的平面角时不要盲目去作,而
应首先由题设去分析,题目中是否已有.能力·思维·方法返回9.正方体ABCD—A1B1C1D1中,E是BC的中点,求平面B1D1E和平面ABCD所成的二面角的正弦值.能力·思维·方法ADBCB1A1D1C1.E解题分析:所求二面角”无棱”,要么先找 “棱”,要么用面积投影.解法一:取B1C1的中点M,.M连接EM,∵E为BC的中点,∴EM⊥平面A1B1D1,∴△B1D1 M是△D1B1E的射影三角形,设平面B1D1E和平面A1B1C1D1所成的
二面角为α,∵平面ABCD//平面A1B1C1D1,∴平面B1D1E和平面ABCD所成的
二面角也为α,设正方体棱长为 a,∴所求二面角的正弦值为返回9.正方体ABCD—A1B1C1D1中,E是BC的中点,求平面B1D1E和平面ABCD所成的二面角的正弦值.能力·思维·方法ADBCB1A1D1C1.F解法二:取BC的中点F,.M连接BD、EF,∴所求二面角的正弦值为.E∵E为BC的中点,∴EF//BD,∵BD//B1D1,∴EF//B1D1,∴EF、B1D1共面,∴平面ABCD∩平面EB1D1F=EF,作BG⊥EF交FE的延长线于G,G连接B1G,则∠B1GB是平面B1D1E和平面ABCD所成二面角的平面角。设正方体棱长为 a,则BE= ,BG= ,在Rt△B1BG中,B1G= ,返回【解题回顾】解法一利用公式 . 思路简单明
了,但计算量较解法二大.解法二的关键是确定二 面角的棱,再通过三垂线定理作出平面角,最终解直 角三角形可求出.能力·思维·方法返回例:如图,已知在正三棱柱ABC-A1B1C1中,侧棱长大于底面边长,M、N分别在侧棱AA1、BB1上,且B1N=A1B1=2A1M,求截面C1MN与底面A1B1C1所成的二面角的大小。返回返回例:S是正△ABC所在平面外一点,SA=SB=SC且∠ASB=∠BSC=∠CSA=90°,M,N分别是AB和SC的中点,求异面直线SM与BN所成的角的余弦值.Paaa返回距离问题一、知识概念1.距离定义
(1)点到直线距离
从直线外一点引一条直线的垂线,这点和垂足之间的距离叫这点到这条直线的距离。
(2)点到平面的距离
从平面外一点引一个平面的垂线,这点和垂足之间的距离叫这点到这个平面的距离。
(3)两平行直线间的距离
两条平行线间的公垂线段的长,叫做两条平行线间的距离。返回(4)两条异面直线间的距离
和两条异面直线分别垂直相交的直线,叫两条异面直线的公垂线;公垂线上夹在两异面直线间的线段的长度,叫两异面直线的距离。
(5)直线与平面的距离
如果一条直线和一个平面平行,那么直线上各点到这个平面的距离相等,且这条直线上任意一点到平面的距离叫做这条直线和平面的距离。
(6)两平行平面间的距离
和两个平行平面同时垂直的直线,叫这两个平行平面的公垂线,它夹在两个平行平面间的公垂线段的长叫做这两个平行平面间的距离。返回2.求距离的步骤
(1)找出或作出有关距离的图形
(2)证明它们符合定义
(3)在平面图形内进行计算返回ABCA1B1D1C1正方体AC1的棱长为1,求下列距离问题(1)A到CD1的距离D点—线返回ABCA1B1D1C1正方体AC1的棱长为1,求下列距离问题(1)A到CD1的距离D(2)A到BD1的距离返回点—线ABCDA1B1C1D1H已知:长方体AC1中,AB=a,AA1=AD=b求点C1到BD的距离?C1H=返回线—线ABCDEF矩形CDFE和矩形ABFE所在的平面相交,EF=5,AD=13,求平行线AB和CD的距离?返回点—面从平面外一点引这个平面的垂线垂足叫做点在这个平面内的射影这个点和垂足间的距离叫做点到平面的距离线面垂直点的射影点面距离返回已知三棱锥P-ABC的三条侧棱PA=PB=PC
试判断点P在底面ABC的射影的位置?PABCOOA=OB=OCO为三角形ABC的外心返回已知三棱锥P-ABC的三条侧棱PA,PB,PC两两垂直,试判断点P在底面ABC的射影的位置?PABCO为三角形ABC的垂心DO返回已知三棱锥P-ABC的顶点P到底面三角形ABC的三条边的距离相等,试判断点P在底面ABC的射影的位置?PABCO为三角形ABC的内心OEF返回已知三棱锥P-ABC的三条侧棱PA=PB=PC
试判断点P在底面ABC的射影的位置?外心已知三棱锥P-ABC的三条侧棱PA,PB,PC两两垂直,试判断点P在底面ABC的射影的位置?垂心已知三棱锥P-ABC的顶点P到底面三角形ABC的三条边的距离相等,试判断点P在底面ABC的射影的位置?内心PABCO返回ABCA1B1D1C1正方体AC1的棱长为1,求下列距离问题D(1)A到面A1B1CD返回ABCA1B1D1C1正方体AC1的棱长为1,求下列距离问题D(1)A到面A1B1CD(2)A到平面BB1D1返回棱长为1的正四面体P——ABC中,求点P到平面ABC的距离?ABCOP返回4.如图,已知P为△ABC外一点,PA、PB、PC两两垂直,且PA=PB=PC=3,求P点到平面ABC的距离。返回3.如图,AB是⊙O的直径,PA⊥平面⊙O,C为圆周上一点,若AB=5,AC=2,求B到平面PAC的距离。返回直角三角形ACB确定平面 ? ,点P在平面 ? 外,
若点P到直角顶点C的距离是24,到两直角边的
距离都是6 ,求点P到平面 ? 的距离?PABCEFO?返回ABEFDCPZ返回线—面一条直线和一个平面平行时,直线上任意一点
到这个平面的距离叫做直线到平面的距离返回例:已知一条直线 l 和一个平面?平行,求证:直线 l 上各点到平面?的距离相等?AA`BB`l返回?lA`AB返回如果一条直线上有两个点到平面的距离
相等,则这条直线和平面平行吗?判断题:返回空间四面体ABCD,问和点A,B,C,D
距离相等的平面有几个?ABCD4ABCD3返回5.如图,已知在长方体ABCD-A’B’C’D’中,棱AA’=5,AB=12,求直线B’C’到平面A’BCD’的距离。练 习返回ABCDPFE已知:ABCD是边长为4的正方形,E,F分别是
AD,AB的中点,PC⊥面ABCD,PC=2,
求点B到平面PEF的距离?GOH点—线点—面线—面综合练习:返回例3:如图:已知ABCD是边长为4的正方形,E、F分别是AB、AD的中点,PC垂直平面ABCD,且PC=2,求点B到平面EFP的距离。解:连AC,BD,设交于O,设AC交EF于HOH连PH因为BD∥平面PEF,所以求B到平面的距离,可转化为求BD到平面的距离过O作OK⊥平面PEF,可证明OK就是所要求的距离K此时,得用△OKH∽△PCH,容易求得 OK的值。返回两个平行平面的距离ABA’B’ 和两个平行平面同时垂直的直线,叫做这两个平面的公垂线。 公垂线夹在平行平面间的部分,叫做这两个平面的公垂线段。直线AA’、BB’都是它们的公垂线段 两个平行平面的公垂线段的长度,叫做两个平行平面的距离。返回返回题型讲练:思考:在边长为1的正方体 中,M,N,E,F分别放 飞 思 维 的 翅 膀 是棱 的中点.(1)求证:平面 面 ;(2)求:平面 与面 的距离.返回思考题:(1999)如图:已知正四棱柱ABCD-A’B’C’D’中,点E在棱DD’上,截面EAC∥D’B,且面EAC与底面ABCD所成的角为450,AB=a
(1)求截面EAC的面积
(2)求异面直线A’B’与AC的距离返回二、例例1:在600二面角M-α-N内有一点P,P到平面M、平面N的距离分别为1和2,求P到直线a距离。解:设PA,PB分别垂直平面M,平面N与A、B,PA,PB所确定的平面为α,且平面α交直线a与Q,设PQ=x在直角△PAQ中sin∠AQP=1/x
在RT △PBQ中sin ∠AQP=2/xcos600=cos(∠AQP +∠AQP),由此可得关于x的方程最后可解得返回例2:菱形ABCD中,∠BAD=600,AB=10,PA⊥平面ABCD,且PA=5,求:
(1)P到CD的距离
(2)P到BD的距离
(3)P到AD的距离
(4)求PC的中点到
平面PAD的距离(1)过P作CD的垂线,交CD的延长线于E,连AEE(2)连BD,交AC于O,连POO返回1. α、β是两个平行平面,aìα,bìβ ,a与b之 间的距离为d1, α与β之间的距离为d2,则 ( )
(A)d1=d2 (B)d1>d2 (C)d1<d2 (D)d1≥d2基础题例题D2. 一副三角板如图拼接,使两个三角板所在的平面互 相垂直.如果公共边AC=a,则异面直线AB与CD的距离 是 ( )
(A) (B) a
(C) (D)C返回3. △ABC中,AB=9,AC=15,∠BAC=120°,△ABC
所在平面外一点P到三个顶点A、B、C的距离都是14,
那么点P到平面α的距离为 ( )
(A)7 (B)9 (C)11 (D)13A基础题例题4. 在长方体, 中,已知AB=4,AA1
=3,AD=1,则点C1到直线A1B的距离为_________.返回5.已知Rt△ABC的直角顶点C在平面α内,斜边 AB∥α,AB=2√6,AC、BC分别和平面α成45°和 30°角,则AB到平面α的距离为______.2基础题例题6.在二面角α- l –β的半平面α内有一点 A 到棱 l 的距
离为 2 ,到半面β所在平面的距离等于 1 ,则这个二面角
的度数为__________________30o 或 150o返回2.已知四面体ABCD,AB=AC=AD=6,BC=3,CD=4,BD=5,求点A到平面BCD的距离。练习:ABD返回7.平面α内的∠MON=60°,PO是平面α的斜线段,PO=3,且PO与∠MON的两边都成45°的角,则点P到α的距离为 ( )
A. B. C. D.A基础题例题8.直线 EF 平行于平面α内的两条直线AB和CD,EF
与α的距离为15,与AB的距离为17,又AB与CD的距
离是28,则EF与CD的距离是 .25或39返回9. 已知平面α∥β, AB⊥α, AB⊥β, A α, B β ,直线 a α,b β, a∥b,A到 a 的距离为2,B 到 b 的距离为5,AB=4,则a,b间的距离为 . 基础题例题ababαβαβABAB返回11.在棱长为1的正方体 中,
(1)求点A到平面 的距离;
(2)求点 到平面 的距离;
(3)求平面 与平面 的距离;
(4)求直线AB与平面 的距离.能力·思维·方法ACDBA1B1D1C1O 解析:
连AC、BD交于O,
AO⊥BD,
又AO⊥DD1,
∴AO⊥平面BD1,
AO的长即为所求返回11.在棱长为1的正方体 中,
(1)求点A到平面 的距离;
(2)求点 到平面 的距离;
(3)求平面 与平面 的距离;
(4)求直线AB与平面 的距离.能力·思维·方法ACDBA1B1D1C1O’E易知平面
A1ACC1⊥平面AB1D1
在矩形AA1CC1中,
易知A1 C⊥O1A
设A1E⊥AO1于E,
∴A1E⊥平面AB1 D1
∴A1E为所求。返回11.在棱长为1的正方体 中,
(1)求点A到平面 的距离;
(2)求点 到平面 的距离;
(3)求平面 与平面 的距离;
(4)求直线AB与平面 的距离.能力·思维·方法ACDBA1B1D1C1EF..易知A1C⊥平面AB1D1
A1C⊥平面BC1D
设直线A1C分别交平
面AB1D1、平面BC1D于
点E、F,则EF的长为
所求
返回11.在棱长为1的正方体 中,
(1)求点A到平面 的距离;
(2)求点 到平面 的距离;
(3)求平面 与平面 的距离;
(4)求直线AB与平面 的距离.能力·思维·方法ACDBA1B1D1C1G.因为直线AB∥平面CDA1B1
∴点B到平面CDA1B1 的距
离BG就是所求的距离,
(G是BC1与B1C的交点,
BG⊥B1C, BG⊥CD,
∴直线BG⊥平面A1B1CD)
此距离为: 返回【解题回顾】(1)求距离的一般步骤是:一作,二证,三计算.即先作出表示距离的线段,再证明它就是要求的距离,然后再计算,其中第二步的证明易被忽视,应引起重视.
(2)求距离问题体现了化归与转化的思想,一般情况下需要转化为解三角形.能力·思维·方法返回12. 已知如图,边长为a的菱形ABCD中,∠ABC=60°,PC⊥平面ABCD,E是PA的中点,求E到平面PBC的距离.能力·思维·方法解:∵E是PA的中点,∴E到平面PBC的距离等于A 到
平面PBC的距离的一半.由PC⊥平面ABCD,得到平面PBC⊥平面ABCD在平面ABCD内作AH⊥BC,
交BC于H,则AH= H所求距离为 返回12. 已知如图,边长为a的菱形ABCD中,∠ABC=60°,PC⊥平面ABCD,E是PA的中点,求E到平面PBC的距离.能力·思维·方法GO返回 距离离不开垂直,因此求距离问题的过程实质上是
论证线面关系(平面与垂直)与解三角形的过程,值得注
意的是,“作、证、算、答”是立体几何计算题不可缺少
的步骤,尤其是证明那一步.误解分析返回13. 在120°的二面角 内有一点P,它到二面角的两个面的距离分别是3cm和4cm,求它在α和β内的射影的距离和这点到 l 的距离.能力·思维·方法解析:设P到α、β的射影分别是M、N,则
PM=3cm,PN=4cm,过P、M、N作平面γ交l于Q则
l⊥γ∴l⊥QM,l⊥QN
∴∠MQN为二面角α-l-β的平面角。
∴∠MQN=120°
∴∠M+∠N=180°
∴P、M、Q、N四点共圆,
∴∠MPN=180°-120°=60°P到 l 的距离是: MN=返回棱柱问题棱锥问题复习:知识网络底面对角线高侧面侧棱顶点棱柱(概念)有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行的几何体。体积V=Sh返回复习:知识网络棱柱(分类)斜棱柱
直棱柱正棱柱返回复习:知识网络四棱柱四棱柱直四棱柱
侧棱垂直底面平行六面体
底面是平行四边形长方体正四棱柱正方体侧面垂直底面返回要点·疑点·考点一、棱柱(1)有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面围成的几何体叫棱柱 1.概念(2)侧棱不垂直于底面的棱柱叫斜棱柱,侧棱垂直于底面的棱柱叫直棱柱,底面是正多边形的直棱柱叫正棱柱 返回(2)两个底面与平行于底面的截面是全等的多边形;2.性质(3)过不相邻的两条侧棱的截面是平行四边形.(1)侧棱都相等,侧面是平行四边形;要点·疑点·考点3.长方体及其相关概念、性质(1)概念:底面是平行四边形的四棱柱叫平行六面体.
侧棱与底面垂直的平行六面体叫直平行六面体.
底面是矩形的直平行六面体叫长方体.
棱长都相等的长方体叫正方体.(2)性质:设长方体的长、宽、高分别为a、b、c,
对角线长为l ,则l2=a2+b2+c2返回复习:知识网络棱锥棱锥正四棱锥正三棱锥正四面体体积V=Sh/3顶点在底面正多边形的射影是底面的中心返回复习:重要定理三垂线定理(逆)作用:1 证明线线垂直;
2 作二面角的平面角。一作一连法返回棱锥基本性质如果棱锥被平行于底面的平面所截,那么截面和底面相似,并且它们面积的比等于截得的棱锥的高与已知棱锥的高的平方比返回棱锥基本性质棱锥的高、斜高和斜高在底面的射影组成一个直角三角形。棱锥的高、侧棱和侧棱在底面的射影组成一个直角三角形PCBDARt⊿ PEHRt⊿ PHBRt⊿ PEBRt⊿ BEH返回正棱锥如果一个棱锥 的底面是正多边形,并且顶点在底面的射影是底面中心这样的棱锥叫做正棱锥返回1、侧面与底面所成的角都相等的棱锥是正棱锥2、棱锥的高可以等于它的一条侧棱长3、棱锥的高一定在棱锥的内部4、侧面均为全等的等腰三角形的棱锥是正棱锥判断正误返回1、三条侧棱相等2、侧棱与底面所成的角相等3、侧面与底面所成的角相等4、顶点P到⊿ABC的三边距离相等5、三条侧棱两两垂直6、相对棱互相垂直7、三个侧面两两垂直外心外心内心内心垂心垂心垂心返回有没有侧棱长和底面边长相等的正四棱锥?有没有侧棱长和底面边长相等的正五棱锥?有没有侧棱长和底面边长相等的正六棱锥?返回1.一个三棱锥,如果它的底面是直角三角形,那么它的三个侧面( )
(A)至多只有一个是直角三角形
(B)至多只有两个是直角三角形
(C)可能都是直角三角形
(D)必然都是非直角三角形C基础题例题返回2.命题:
①底面是正多边形的棱锥,一定是正棱锥;
②所有的侧棱的长都相等的棱锥,一定是正棱锥;
③各侧面和底面所成的二面角都相等的棱锥,一定是正棱锥;
④底面多边形内接于一个圆的棱锥,它的侧棱长都相等;
⑤一个棱锥可以有两条侧棱和底面垂直;
⑥一个棱锥可以有两个侧面和底面垂直.
其中正确的有 ( )
(A)0个 (B)1个 (C)3个 (D)5个C基础题例题返回基础题例题2.正三棱柱ABC-A1B1C1中,若AB=√2 BB1,则AB1
与C1B所成角的大小是 ( )
A.60o B.90o C.105o D.75o
B返回3.长方体三边之和为a+b+c=6,总面积为11,则 其对角线长为__;若一条对角线与二个面所成的 角为30°或45°,则与另一个面所成的角为 ___;若一条对角线与各条棱所成的角为α、 β、γ,则sinα、sinβ、sinγ的关系为_____
___________________________.sin2α+sin2β+sin2γ=2基础题例题530°返回设棱锥的底面积是8cm2,则这个棱锥的中截面(过棱锥的高的中点且平行于底面的截面)的面积是多少?S中=2返回过棱锥的高的三等分点作两个平行于底面的截面,它将棱锥的侧面分为三部分面积之比(自上而下)为 。返回过棱锥的高作两个平行于底面的截面,它将棱锥的侧面分为三部分面积相等则它分棱锥的高的比是(自上而下) 。返回正三棱锥的底面边长为a.侧棱长为b,求它的高和侧面积?PABCO返回正三棱锥的底面边长为1.侧面与底面所成的角为60,求它的高和相邻两侧面所成的二面角的大小?PABCO返回正四棱锥的底面边长为1.侧面与底面所成的角为60,求它的高和相邻两侧面所成的二面角的大小?PABDCO返回正三棱锥的底面边长为a .侧棱与底面所成的角为60,过底面一边做一截面使其与底面成30的二面角,求此截面面积?PABCO返回 已知:三棱锥P-ABC的底面是等腰三角形,AB=AC=10,BC=12,棱锥的侧面与底面所成的二面角都是45,求棱锥的侧面积?返回连接棱长都是a的正三棱锥的侧面中心成一个三角形,求此三角形的面积?PABC返回在正四棱锥内有一个内接正方体,这正方体的四个顶点在四棱锥的侧棱上,另四个顶点在棱锥底面上,若棱锥底面边长为a,高为h,求内接正方体的棱长?ABDCOPH设内接正方体的棱长为x返回在正三棱锥P-ABC的底面边长和高都是4,其内接正三棱柱的三个侧面都是正方形,求内接正三棱柱的全面积?返回能力·思维·方法4. 在底面是直角梯形的四棱锥P-ABCD中,
侧棱PA⊥底面ABCD,∠ABC=90°,PA=AB=BC=2,AD=1, (1)求D到平面PBC的距离;
(2)求面PAB与面PCD所成的二面角的大小。?解: (1)∵AD//平面PBC∴D到平面PBC的距离等于A到平面PBC的距离∵PA⊥BC, AB⊥BC∴BC⊥平面PAB∴平面PBC⊥平面PAB∴A到PB的距离就是A到平面PBC的距离∵PA=AB=2, PA⊥AB,∴A到PB的距离为∴D到平面PBC的距离为返回能力·思维·方法4. 在底面是直角梯形的四棱锥P-ABCD中,
侧棱PA⊥底面ABCD,∠ABC=90°,PA=AB=BC=2,AD=1, (1)求D到平面PBC的距离;
(2)求面PAB与面PCD所成的二面角的大小。?Q (2)延长CD与BA相交于Q,∵AD∥BC,且 AD= BC∴A是QB的中点,又PA=AB=AQ∴BQ⊥PQ,又∵BC⊥平面PAB,∴CP⊥PQ,故∠CPB是所求二面角的
平面角,故面PCD与面PCD所成的二面角为返回例题讲解1、四棱锥P-ABCD的底面是边长为a的正方形,PB⊥面ABCD.
(1)若面PAD与面ABCD的二面角为600,求四棱锥的体积;作、证、求?∵ PB⊥面ABCD,BA⊥AD, ∴PA⊥AD ∴∠PAB就是面PAD与面ABCD的二面角的平面角解:即∠PAB=600V= a3返回例题讲解1、四棱锥P-ABCD的底面是边长为a的正方形,PB⊥面ABCD.
(2)证明不论高PB怎样变化,面PAD与面PCD所成的二面角恒大于900.M证:由题设侧面PAD与PCD为全等⊿,作CM⊥PD于M,连结MA,则⊿CDM≌⊿ADM,∴AM=CM,∠AMD=900故AMC就是所证二面角的平面角.连结AC在⊿AMC中,由余弦定理
cos∠AMC =故∠AMC>900,即证. 小结:作二面角平面角的方法
●有面的垂线,则一作一连法
●定义法,在两面内作棱的垂线
●面积射影定理返回变化一 四棱锥P-ABCD的底面是边长为a的菱形,∠BCD=600,PB⊥面ABCD.若面PAD与面ABCD的二面角为600,求四棱锥的体积;E返回 四棱锥P-ABCD的底面是边长为a的菱形,∠BCD=600,面PBC⊥面ABCD,且⊿PBC是等边⊿. 求侧面PAD与底面ABCD所成的二面角;变化二E注意:●面面垂直的应用
●分析平面图形返回例题讲解2、如图在直三棱柱ABC-A1B1C1中,底面ABC是等腰Rt⊿, ∠C=900 ,D、E分别是CC1和A1B的中点,AC=AA1=2
(1)求线段DE的长返回例题讲解2、如图在直三棱柱ABC-A1B1C1中,底面ABC是等腰Rt⊿, ∠C=900 ,D、E分别是CC1和A1B的中点,AC=AA1=2
(2)求二面角A-BD-C的大小(反三角表示)解:∵ ABC-A1B1C1是直棱柱,AC⊥BC,∴AC⊥侧面BB1C1C,作CM⊥BD于M,连结AM,则∠AMC就是所求二面角的平面角;在⊿ACM中,AC=2∴tan∠AMC=AC/CM=即所求为AC⊥CM,返回例题讲解3、如图在直三棱柱ABC-A1B1C1中,底面ABC是等腰Rt⊿,∠C=900 ,D、E分别是CC1和A1B的中点,AA1=2,若点E在平面ABD上的射影是⊿ABD的重心G.
(1)求A1B与平面ABD所成的角(用反三角表示);解:连结BG,由已知∠EBG就是所求的角,…… ……∴A1B与平面ABD所成的角为返回例题讲解3、如图在直三棱柱ABC-A1B1C1中,底面ABC是等腰Rt⊿,∠C=900 ,D、E分别是CC1和A1B的中点,AA1=2,若点E在平面ABD上的射影是⊿ABD的重心G.
(2)求点A1到平面AED的距离。方法A:作垂线法方法B:等体积法返回3、如图在直三棱柱ABC-A1B1C1中,底面ABC是等腰Rt⊿,∠C=900 ,D、E分别是CC1和A1B的中点,AA1=2,若点E在平面ABD上的射影是⊿ABD的重心G.
(2)求点A1到平面AED的距离。解A:由上题解知,DE⊥平面AA1B1B∴平面ADE⊥平面AA1B1B于AE在⊿A1AB1中,A1K=方法A:作垂线法返回3、如图在直三棱柱ABC-A1B1C1中,底面ABC是等腰Rt⊿,∠C=900 ,D、E分别是CC1和A1B的中点,AA1=2,若点E在平面ABD上的射影是⊿ABD的重心G.
(2)求点A1到平面AED的距离。解B:方法B:等体积法方法C:对象转换法返回小结:1、联想概念及其性质;
2、分解难点,掌握各类基本作图;
3、强调作证求过程;
4、空间问题平面化,尤三角形内
的计算。返回面积问题体积问题返回返回返回基础题例题C1.设棱锥的底面面积为8cm2,那么这个棱锥的中截面
(过棱锥的中点且平行于底面的截面)的面积是( )
(A)4cm2 (B) cm2 (C)2cm2 (D) cm22. 一个锥体被平行于底面的平面所截,若截面面积 是底面面积的四分之一,则锥体被截面截得的一个小 锥与原棱锥体积之比为 ( )
(A)1 : 4 (B) 1 : 3 (C) 1 : 8 (D) 1 : 7 C返回A3.设长方体三条棱长分别为a,b,c,若长方体所有棱的
长度之和为24,一条对角线长度为5 ,体积为2,则
等于 ( )
(A) (B) (C) (D)基础题例题返回C4.斜三棱柱的一个侧面的面积为S,另一条侧棱到这个
侧面的距离是a,则这个三棱柱的体积是 ( )
(A) (B) (C) (D)基础题例题5.在侧棱长为2√3,每个侧面的顶角均为40°的正三棱锥P-ABC中,过A作截面分别交PB、PC于E、F,则△AEF的最小周长是 ( )
(A) 6 (B) (C) 36 (D) A返回例.设P是棱长相等的四面体内任意一点,则P到各个面的距离之和是一个定值,这个定值等于( )。 (A)四面体的棱长 (B)四面体的斜高 (C)四面体的高 (D)四面体两对棱间的距离提示:用体积法求解 返回解:如图正四面体ABCD中,过点A作四面体的高AO,则由点P分别连接PA、PB、PC、PD,得到四个小四面体,
若点P到四个表面的距离分别为h1、h2、h3、h4,那么四面体被分成的四个小四面体,它们的体积和恰好是四面体ABCD的体积,返回∴ VABCD=VPBCD+VPABC+VPABD+VPACD,
∴
∴ h1+h2+h3+h4=AO. 选C.返回例.若正四棱柱的底面积为P,过相对两侧棱的截面面积是Q,则该四棱柱的体积是( )。 (A) (B) (C) (D)返回解:如图,设四棱柱底面边长AB=a,高AA1=b,则P=a2,过两侧棱AA1、CC1的截面面积Q= ab,∴ 返回6.若一个斜棱柱A1B1C1—ABC的底面是等腰△ABC,它的三边边长分别是AB=AC=10cm,BC=12cm,棱柱的顶点A1与A、B、C三点等距,且侧棱AA1=13cm,求此棱柱的全面积.解:自B引BD⊥AA1于D,连接CD,D∵AA1=A1B=A1C,底面△ABC为等腰△,故顶点A1在底面ABC上的射影O在底边
BC的高AE上,OE由三垂线定理知,BC⊥AA1,即侧面B1BCC1为矩形,由AA1⊥BC,AA1⊥BD,
得AA1⊥平面BDC,∴AA1⊥CD,在△A1AB中,引A1F⊥AB于F,F在Rt△A1FA中,由A1A=13,AF=5,A1F=12,得则BD=AB×sin∠A1AB=10×∴S柱侧=(BD+DC+BC)×A1A=396,又在△ABC中,AE⊥BC,AB=10,BE=6,得AE=8,∴S△ABC=8,∴S柱全=396+2×48=492(cm) 2返回7.已知E,F分别是棱长为a的正方体ABCD—A1B1C1D1的棱A1A,CC1的中点,求四棱锥C1—B1EDF的体积.能力·思维·方法...FE解:方法一:连接A1C1, B1D1交于O1,O1过O1作O1H⊥ B1D于H,H∵EF//A1C1, ∴A1C1//平面B1EDF ∴C1到平面B1EDF的距离 就是
A1C1就是 到平面B1EDF的距离∵平面B1D1D⊥平面B1EDF,∴O1H⊥平面B1EDF 即O1H为棱锥的高 ∵△B1O1H∽△B1DD1返回7.已知E,F分别是棱长为a的正方体ABCD—A1B1C1D1的棱A1A,CC1的中点,求四棱锥C1—B1EDF的体积.能力·思维·方法..FE解:方法二:连接EF设B1到平面C1EF的距离为h1,D到平面C1EF的距离为h2 ,则 h1+h2=B1D1=√2a , 返回7.已知E,F分别是棱长为a的正方体ABCD—A1B1C1D1的棱A1A,CC1的中点,求四棱锥C1—B1EDF的体积.能力·思维·方法..FE解:方法三:返回将边长为a的正方形ABCD沿对角线AC折起,使B,D两点间距离变为a,求所得三棱锥D-ABC的体积?ABCD返回将边长为a的正方形ABCD沿对角线AC折起,使B,D两点间距离变为a,求所得三棱锥D-ABC的体积?ABCD返回正方体ABCD-A1B1C1D1中,E,F分别是BB1,DD1的中点,棱长为a,求四棱锥D1-AEC1F的体积?EF返回平行六面体中,已知AB=AD=2a,AA1=a,∠ A1AD= ∠ A1AB= ∠ DAB= 60°(1)求证:AA1⊥面B1CD1A1B1C1D1ABCD返回A1B1C1D1ABCD平行六面体中,已知AB=AD=2a,AA1=a,∠ A1AD= ∠ A1AB= ∠ DAB= 60°(1)求证:AA1⊥面B1CD1返回(2)求平行六面体的体积?A1B1C1D1ABCDV= SA1B1CD1×CECE=SA1B1C1D1==平行六面体中,已知AB=AD=2a,AA1=a,∠ A1AD= ∠ A1AB= ∠ DAB= 60°(1)求证:AA1⊥面B1CD1返回A1B1C1D1ABCDS⊿B1CD1=VC1-B1CD1= S⊿B1CD1×CC1(2)求平行六面体的体积?平行六面体中,已知AB=AD=2a,AA1=a,∠ A1AD= ∠ A1AB= ∠ DAB= 60°(1)求证:AA1⊥面B1CD1返回A1B1C1D1ABCDS⊿B1CD1=VC1-B1CD1= S⊿B1CD1×CC1== S⊿B1C1D1×hV= ( 2 S⊿B1C1D1)×h(2)求平行六面体的体积?平行六面体中,已知AB=AD=2a,AA1=a,∠ A1AD= ∠ A1AB= ∠ DAB= 60°(1)求证:AA1⊥面B1CD1返回求多面体的体积时常用的方法直接法割补法变换法根据条件直接用柱体或锥体的体积公式如果一个多面体的体积直接用体积公式计算用困难,可将其分割成易求体积的几何体,逐块求积,然后求和。如果一个三棱锥的体积直接用体积公式计算用困难,可转换为等积的另一三棱锥,而这一三棱锥的底面面积和高都是容易求得返回求棱长为a的正四面体的体积.返回已知正三棱锥的侧面积是18 ,高为3,求它的体积?返回若正四棱锥的底面积是S,侧面积是Q,则它的体积为?返回过棱锥的高的三等分点作两个平行于底面的截面,它将棱锥分为三部分体积之比(自上而下)为 。返回PABC三棱锥P-ABC的三条侧棱两两垂直,PA=a, PB=b, PC=c , ⊿ABC的面积为S求点P到底面ABC的距离返回ABCDPFE已知:ABCD是边长为4的正方形,E,F分别是AD,AB的中点,PC⊥面ABCD,PC=2,
求点B到平面PEF的距离?GOH点—线点—面线—面返回ABCDPFEG= S⊿BFE×PC= S⊿PFE×h已知:ABCD是边长为4的正方形,E,F分别是AD,AB的中点,PC⊥面ABCD,PC=2,
求点B到平面PEF的距离?返回斜三棱柱ABC-A`B`C`的侧面BB`C`C的面积为S,AA`到此侧面的距离是a,求此三棱柱的体积?返回ABCA`B`C`斜三棱柱ABC-A`B`C`的侧面BB`C`C的面积为S,AA`到此侧面的距离是a,求此三棱柱的体积?返回如图,在多面体ABCDEF中,已知面ABCD是边长为3的正方形,EF//AB,EF=1.5, EF与面AC的距离为2,求此多面体的体积?=4.5=3返回=6=1.5如图,在多面体ABCDEF中,已知面ABCD是边长为3的正方形,EF//AB,EF=1.5, EF与面AC的距离为2,求此多面体的体积?返回正三棱柱ABC-A1B1C1的底面边长为3,侧棱长为4,求四面体ABB1C1的体积返回已知三棱锥有一条棱长为4,其余各棱长为3,求其体积?返回已知三棱锥有一条棱长为4,其余各棱长为3,求其体积?返回已知三棱锥P-ABC中,PA=1,AB=AC=2, ∠ PAB= ∠PAC= ∠BAC= 60°,求三棱锥的体积?返回已知三棱锥P-ABC中,PA=1,AB=AC=2, ∠ PAB= ∠PAC= ∠BAC= 60°,求三棱锥的体积?解法一直接法返回解法二变换法已知三棱锥P-ABC中,PA=1,AB=AC=2, ∠ PAB= ∠PAC= ∠BAC= 60°,求三棱锥的体积?返回解法三割补法已知三棱锥P-ABC中,PA=1,AB=AC=2, ∠ PAB= ∠PAC= ∠BAC= 60°,求三棱锥的体积?返回解法四割补法已知三棱锥P-ABC中,PA=1,AB=AC=2, ∠ PAB= ∠PAC= ∠BAC= 60°,求三棱锥的体积?返回例:如图已知正三棱锥S — ABC中,E、F分别是SB、SC 的中点,平面AEF⊥平面SCB.
求证:三棱锥S—ABC侧面 积与底面积的比。解:作正棱锥的高SO,连结AO并延长交BC于D,
连结SD交EF于G,连结AG.
GO返回设正三棱锥S—ABC的底面边长为 ,则AD= ,SA=SB=返回ABCSD例1、已知三棱锥的两个侧面都是边长为 的等边三角形,另一个侧面是等腰直角三角形。求此三棱锥的体积。法一:取AB中点D,连接SD,CD。
易得△ABC为等腰直角三角形,?ACB=90o。则有SD⊥AB,
CD⊥AB。又SA=SB=SC,
∴S在底面的射影为底面的外心,
即点D,∴SD⊥平面ABC。
∴由VS-ABC= S△ABC?SD得三棱锥体积。返回例、已知三棱锥的两个侧面都是边长为 的等边三角
形,另一个侧面是等腰直角三角形。求此三棱锥的体积。
ABCSEF注意:分割法求体积。解法二
提示:设三棱锥S-ABC,侧面SAC、SBC为等边三角形,边长为 ,SA?SB。取SA中点E,AB中点F,连接AE、BE、EF。可证得:SC ?平面ABE。利用:VS-ABC=VS-ABE+VC-ABE
得三棱锥体积。(KEY: )返回例、在棱长为a的正方体ABCD-A1B1C1D1中,求D1到截面C1BD的距离。ABCDA1B1C1D1提示:利用 = 求解。注意:等体积法求点面距离。KEY:返回例:如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
证明:D1E⊥A1D ;
当E为AB的中点时,求点E到面ACD1的距离;
AE等于何值时,二面角D1-EC-D的大小为等体积法求点面距离返回PBCDEA例:已知四棱锥P—ABCD ,PB⊥AD,侧面PAD为边长等于2的正三角形,底面ABCD为菱形,侧面PAD与底面ABCD所成的二面角为120。
(Ⅰ)求点P到平面ABCD的距离;(Ⅱ)求面APB与面CPB所成二面角的大小。等体积法求点面距离通过以上的解答,我们不难看出等体积法在处理点到面的距离和体积时非常有效,因此我们在平时的学习中应该掌握.利用等体积法我们能够从侧面迂回地解决一些从正面较难下手的问题——这是数学中的一种重要思想方法.在利用等体积法时我们应该在原图
形中寻找到一个较容易计算出面积及其高的面来。返回例:正三棱锥的侧面积为18 cm2,高为3cm.被一个过底面中心且平行于一个侧面的平面所截,求这个截面与底面所成的角和面积O解:过底面△ABC的中心O作OD∥BC,交AB、AC于D、E,过DE作平面DEF ∥平面VBC,与平面ABV、平面ACV分别交于DF、EF。设正三棱锥底面边长为 cm,AO与BC交于C,连VG设VG=h cm返回∴ S侧=3× × ×h=18在△VOG中 VG2 =VO2 +OG2
VO = 3
OG = ×解①②得h=2 =6 S截面= × DE×OF
DE= =4
OF= VG=∠AGV= ∠AOF=600返回体积问题: V棱柱=sh V棱锥= shD返回练习:
1.正方体的棱长位 , 以它的上底面中心以及下底面各边中点为顶点的四棱锥的侧面积是_______.
2.已知三棱锥的两个面是边长为 的正三角形,另外两个面是等腰直角三角形,则此三棱锥的体积____________.返回C3.设棱锥的底面面积为8cm2,那么这个棱锥的中截面
(过棱锥的中点且平行于底面的截面)的面积是( )
(A)4cm2 (B) cm2
(C)2cm2 (D) cm2返回4.若一个锥体被平行于底面的平面所截,若截面面积 是底面面积的四分之一,则锥体被截面截得的一个小 锥与原棱锥体积之比为( )
(A)1 : 4 (B) 1 : 3
(C) 1 : 8 (D) 1 : 7 C返回A5.设长方体三条棱长分别为a,b,c,若长方体所有棱的
长度之和为24,一条对角线长度为5 ,体积为2,则
等于( )
(A) (B)
(C) (D)返回C6.斜三棱柱的一个侧面的面积为S,另一条侧棱到这个
侧面的距离是a,则这个三棱柱的体积是( )
(A) (B)
(C) (D)返回A7.在侧棱长为23,每个侧面的顶角均为40°的正三棱锥P-ABC中,过A作截面分别交PB、PC于E、F,则△AEF的最小周长是( )
(A) 6 (B)
(C) 36 (D) 返回8. 如图,在多面体ABCDE中,AE⊥面ABC,BD∥
AE,且AC=AB=BC=BD=2,AE=1,F为CD中点.
(1)求证:EF⊥面BCD;
(2)求多面体ABCDE的体积;
(3)求面CDE与面ABDE所成的二面角的余弦值.【解题回顾】对于不规则几何体一定要能识别其本质,本题的多面体实际上是倒着的四棱锥.返回9.在三棱锥P-ABC中,PA、PB、PC两两成60°角,PA=a,PB=b,PC=c,求三棱锥P-ABC的体积. 【解题回顾】(1)把A、B、C中的任一个点作为顶点(其余三点构成的三角形作为底面)是解题的关键,这说明改变几何体的放置方式或改变对几何体的观察角度在解题中是十分重要的.
(2)当a=b=c时,得到正四面体的体积是?.
(3)若在PA、PB、PC上各任取一点M、N、R,设PM=
m,PN=n,PR=r,则容易证明 ,这一结论与
PA、PB、PC成多大的角无关.返回10.若一个斜棱柱A1B1C1—ABC的底面是等腰△ABC,它的三边边长分别是AB=AC=10cm,BC=12cm,棱柱的顶点A1与A、B、C三点等距,且侧棱AA1=13cm,求此棱柱的全面积.【解题回顾】求斜棱柱全面积的基本方法是求出各个侧面的面积与底面积.本题求侧面积时也可以用直截面BCD的周长去乘AA1而得到.E返回误解分析1.求斜棱柱的全面积,除直截面周长乘侧棱长这个公式外,大多采用逐一求出各表面面积,然后作和的方法,因此不要盲目套什么公式,或在相加时,漏了上、下底面积2.求三棱锥的体积非常灵活,有直接法、割补法、颠倒顶点法等,不管用何种方法,一定要看清字母位置,更不能漏乘1/3.返回与球的多面体问题例.一个凸多面体的棱数为30,面数为12,则它的各面多边形的内角总合是( )(A)5400° (B)6480° (C)7200° (D)7920°提示:运用“欧拉定理” E+2=V+F。返回解:根据欧拉定理 V=(E+2)-F=32-12=20.
设该多面体的12个面的边数分别为E1,E2,……,E12,
那么共有棱数30= ( E1+E2+……+E12),
∴ E1+E2+……+E12=60,
12个面中每个面的内角为
(i=1,2,……,12),
∴ 内角总合为
=6480°,∴ 选B.返回已知凸多面体每个面都是五边形,每个顶点都有三条棱,试求该多面体的面数、顶点数和棱数.返回A1.一个四面体的所有棱长都为√2,四个顶点在同一球面上,则此球的表面积为 ( )
(A) (B) (C) (D)基础题例题2.地球表面上从A地(北纬45°,东经120°)到B地(北纬
45°,东经30°)的最短距离为(地球半径为R) ( )
(A)R (B) (C) (D)C3.在北纬45o的圈上有甲、乙、丙三地,甲乙、乙丙之间
的经度差都是90o,则甲丙两地的球面距离是甲乙两地球
面距离的 ______倍 返回基础题例题C4.球的表面积膨胀为原来的 2 倍,膨胀后的体积为原来的
( )
A. √2倍 B.2倍 C.2√2倍 D.4倍5.棱长为2的正四面体的体积为_____________6.设P、A、B、C是球O面上的四点,且PA、PB、PC两两
互相垂直,若PA=PB=PC=a, 则球心O到截面ABC的距离
是______________返回能力·思维·方法7.求正八面体每相邻两个面所成二面角的大小。ABCFDE解:如图,设棱长为 a,AE中点为F, 连接BF、DF, ∵△ABE,△ADE是正三角形, ∴BF⊥AE,DF⊥AE, ∴∠BFD是二面角B-AE-D的平面角, △BDF中,BF=DE= BD= ∴所求二面角为π- arccos 返回三棱锥A-BCD的两条棱AB=CD=6,其余各棱长均为5,求
三棱锥的内切球半径.E解:取CD的中点E,连接AE,BE,由CD⊥AE,CD⊥BE,得CD⊥平面ABE又AD=5,DE=3,得AE=BE=4,故△ABE的面积为3√7于是,VA-BCD=VC-ABE+VD-ABE显然,三棱锥的三个侧面全等,各侧面的面积为12,设三棱锥的内切球半径为 r,则VA-BCD= (SABC+SBCD+SCDA+SDAB)·r= · 48r =16r 由16r=6√7 得内切球的半径为 返回【解题回顾】
正如三角形的内切圆经常与面积发生关 系一样,多面体的内切球的半径也常与体积发生联系.能力·思维·方法返回例题选讲OO2O1返回能力·思维·方法9.在球内有相距14cm 的两个平行截面,它们的面积分别是
64πcm2 和 36πcm2,求球的表面积。.解:设球半径为R,(1)当截面在球心同侧,如图(1)(1)则有√R2-36-√R2-64=14 而此方程无解,故截面在球心的同侧
不可能。(2)当截面在球心异侧,如图(2)(2)则有√R2-36 +√R2-64=14解得 R=10 ∴S球面=4πR2=400π(cm)2返回返回返回将一个半径为1的球投入底面边长是4的正四棱柱型盛水容器中,求水面上升的高度?返回将一个半径为1的球投入底面边长是4的正四棱柱型盛水容器中,求水面上升的高度?返回求正方体的内切球和它的外接球的表面积之比返回求正四面体的内切球和它的外接球的体积之比HO返回半球的半径为R,一正方体的四个顶点在半球的底面上,另四个顶点在球面上,求正方体的棱长返回例:共端点M的三条线段MA、MB、MC两两垂直,过M、A、B、C刚好可作一个半径为2的球,则MA、MB、MC的平方和为( ) 解:以MA、MB、MC为棱作长方体,那么这个长方体的八个顶点都在球上,且长方体的对角线恰好是球的直径,所以球的直径d=4,
而MA2+MB2+MC2=d2=16.返回延伸·拓展过半径为R的球面上一点作三条两两垂直的弦MA、MB、MC.
(1)求证:MA2+MB2+MC2为定值;
(2)求三棱锥M-ABC的体积的最大值.【解题回顾】(1)MA、MB、MC两两垂直.根据球的对称性,采用补形的方法,可以把它补成一个球的内接长方体.长方体的对角线的平方就是球的直径的平方,即MA2+MB2+MC2=4R2.在做选择题、填充题时就可直接用这个结论.
(2)在球中的线段计算问题,常转化为小圆半径,大圆半径及球心到截面距离来解决. 返回返回误解分析1.在涉及球内接正方体或长方体的题目中,作出的截面一般过多面体的对角线,且对角线长为球的直径?若过对棱中点作横截面,将会出错.2.球面上两点间距离不是直线距离,也不是纬度圈上的劣弧长,而是指过这两点的球大圆上 的劣弧长,不能错啊!返回例:如图所示,在纬度为α的北纬纬线上有一点A,其中α是△AOO’的三内角的等差中项,而t是 与 的等比中项,当地球自转t小时后,求点A转动前后的球面距离.返回解:由题意得 α=60° ,
, t=6,设点A转动后为点B,由于地球转一圈需24小时,因此6小时转了圆周长的 ,
所以∠AO’B=90°, ∠OAO’=30°,所以∠AO’B=90°, ∠OAO’=30°,
所以AO’=Rsin30°= R=BO’, AB= R, 返回返回A1.一个四面体的所有棱长都为2,四个顶点在同一球面上,则此球的表面积为( )
(A) (B) (C) (D)A2.已知一个简单多面体的各个顶点处都有三条棱,则顶点数V与面数F满足的关系式是( )
(A)2F+V=4 (B)2F-V=4
(C)2F+V=2 (D)2F-V=2返回A3.一个凸多面体的顶点数为20,棱数为30.则它的各面多边形的内角总和为( )
(A)2160° (B)5400° (C)6480° (D)7200°A4.将棱长为3的正四面体的各棱长三等分,经过靠近顶点的各分点,将原正四面体各顶点均截去一个棱长为1的小正四面体,剩下的多面体的棱数为( )
(A)16 (B)17 (C)18 (D)19返回A5.地球表面上从A地(北纬45°,东经120°)到B地(北纬
45°,东经30°)的最短距离为(地球半径为R)( )
(A)R (B)
(C) (D)返回翻折问题生活问题 如图,以等腰直角三角形斜边BC上的高AD为折痕,使⊿ ABD和⊿ ACD折成相垂直的两个面。
求证:(1)BD⊥CD;(2)∠ BAC=60°.ABCD返回 例:已知:E、F是正方形ABCD的边BC和CD的中点,分别沿AE、EF、AF将⊿ABE、 ⊿ECF、⊿AFD折起,使B、C、D三点重合于P点,如图所示。
(1)求证:AP ⊥ EF;
(2)?求二面角A-EF-P的大小。
返回解:(1)∵AP⊥PF,AP ⊥PE,
PE∩PE=P
∴ AP⊥平面PEF
又∵EF 平面PEF
∴AP ⊥EF.返回(2)取EF的中点H,连结PH、AH,
∵PE=PF,AE=AF ∴AH ⊥EF,PH ⊥EF
∴ ∠AHP是二面角A-EF-P的平面角。
由(1)知AP ⊥平面PEF,而PH 平面PEF
∴AP ⊥PH,即⊿ APH是Rt⊿.
∴ cos∠AHP= , ∠ AHP=arcos
∴二面角A-EF-P的大小为arcos 。
返回 例:在矩形ABCD中,AB=3,BC=4,沿对角线BD对折成二面角A-BD-C,使A在平面BCD上的射影在BC上。
(1)求异面直线AB与CD所成的角;
(2) 求AB和CD间的距离。
返回 例3:已知Rt⊿ABC中,AB=3,BC=4,E是斜边AC边上的一点,沿BE将ABE折起,使二面角A-BE-C是直二面角,当AC最短时,求∠ABE的大小。
返回练习
1、长方体ABCD-A1B1C1D1中,AB=3,
BC=2,AA1=1,一蚂蚁从点A沿其表面爬
到C1点的最短路程为( )
A、 B、 C、 D、
返回 2、如图代表未折叠正方体的展开图,将其折叠起来,变成正方体后图形是( )
返回5.如图是正方体的平面展开图,在这个正方体中①BM与ED平行;
②CN与BE是异面直线;
③CN与BM成60°的角;
④DM与BN垂直。以上四个命题中,正确
命题的序号是( ) ③ ④返回复习小结
1、解折叠问题首先是准确地画出原来的平面图形及折叠后的空间图形,对照两图形中对应元素的位置、大小、形状,确定不变元素,不变量是解题的基础,折叠所成的二面角往往是解题的关键。返回 2、求侧面上两点间的最短距离,一般都是将空间图形沿某一条棱或母线剪开铺平,化为求两点决定的线段长, 从而化“曲”为“直”,化“折”为“平”。展开是空间问题平面化的一种常用方法。返回一个立方体的六个面上分别标有字母A、B、C、D、F,下图是此立方体的两种不同放置,则与D面相对的面上的字母是 ( )
B返回如图,以长方体ABCD-A1B1C1D1的顶点为顶点且四个面都是直角三角形的四面体是__________
(注:只写出其中的一个,并在图中画出相应的四面体)
返回一间民房的屋顶有如图所示三种不同的盖法:①单向倾斜;②双向倾斜;③四向倾斜.记三种盖法屋顶面积分别为P1、P2、P3.若屋顶斜面与水平面所成的角都是α,则
( )?
(A)P3>P2>P1
(B)P3>P2=P1
(C)P3=P2>P1?
(D)P3=P2=P1?
D返回已知甲烷CH4的分子结构是:中心一个碳原子,外围有4个氢原子(这4个氢原子构成一个正四面体的四个顶点).设中心碳原子到外围4个氢原子连成的四条线段两两组成的角为θ,则cosθ等于 ( )
(A)-1/3 (B)1/3
(C)-1/2 (D)1/2A返回在直角坐标系xoy中,点A、B、C、D的坐标分别为(5,0)、(-3,0)、(0,-4)、(-4,-3),
将坐标平面沿y轴折成直二面角.
(1)求AD、BC所成的角;
(2)BC、OD相交于E,作
EF⊥AD于F,
求证:EF是AD、BC的公垂
线,并求出公垂线段EF的长;
(3)求四面体C-AOD的体积.【解题回顾】这是一道与解几结合的翻折题,画好折后
图将原平面图还原成四棱锥,进一步用三垂线定
理证明AD⊥BC.
返回(1)给出两块相同的正三角形纸片(如图1,图2),要求用其中一块剪拼成一个正三棱锥模型,另一块剪拼成一个正三棱柱模型,使它们的全面积都与原三角形的面积相等,请设计一种剪拼方法,分别用虚线标示在图1、图2中,并作简要说明;
(2)试比较你剪拼的正三棱锥与正三棱柱的体积的大小;
(3)(本小题为附加题)
如果给出的是一块任意三角形的纸片(如图3),要求剪拼成一个直三棱柱模型,使它们的全面积与给出的三角形的面积相等,请设计一种剪拼方法,用虚线标示在图3中,并作简要说明.图1图2返回【解题回顾】本题是2002年高考题,是一道集开放、探索、动手于一体的优秀考题,正三角形剪拼正三棱柱除参考答案的那种剪法外,还可以用如图4的剪法,当然参考答案的剪法是其本质解,因为它为(3)的解答提供了帮助.图1图2图3图4返回5.如图(甲),从三棱锥P-ABC的顶点P沿着三条侧棱PA、PB、PC剪开成平面图形,得到△P1P2P3(如图(乙)),且P1P2=P2P3.(1)在三棱锥P-ABC中,求证:PA⊥BC.
(2)若P1P2=26,P1P3=20,求三棱锥P-ABC的体积.返回综合问题例题讲解1、四棱锥P-ABCD的底面是边长为a的正方形,PB⊥面ABCD.
(1)若面PAD与面ABCD的二面角为600,求四棱锥的体积;作、证、求?∵ PB⊥面ABCD,BA⊥AD, ∴PA⊥AD ∴∠PAB就是面PAD与面ABCD的二面角的平面角解:即∠PAB=600V= a3返回例题讲解1、四棱锥P-ABCD的底面是边长为a的正方形,PB⊥面ABCD.
(2)证明不论高PB怎样变化,面PAD与面PCD所成的二面角恒大于900.M证:由题设侧面PAD与PCD为全等⊿,作CM⊥PD于M,连结MA,则⊿CDM≌⊿ADM,∴AM=CM,∠AMD=900故AMC就是所证二面角的平面角.连结AC在⊿AMC中,由余弦定理
cos∠AMC =故∠AMC>900,即证. 小结:作二面角平面角的方法
●有面的垂线,则一作一连法
●定义法,在两面内作棱的垂线
●面积射影定理返回变化一 四棱锥P-ABCD的底面是边长为a的菱形,∠BCD=600,PB⊥面ABCD.若面PAD与面ABCD的二面角为600,求四棱锥的体积;E返回 四棱锥P-ABCD的底面是边长为a的菱形,∠BCD=600,面PBC⊥面ABCD,且⊿PBC是等边⊿. 求侧面PAD与底面ABCD所成的二面角;变化二E注意:●面面垂直的应用
●分析平面图形返回例题讲解2、如图在直三棱柱ABC-A1B1C1中,底面ABC是等腰Rt⊿, ∠C=900 ,D、E分别是CC1和A1B的中点,AC=AA1=2
(1)求线段DE的长返回例题讲解2、如图在直三棱柱ABC-A1B1C1中,底面ABC是等腰Rt⊿, ∠C=900 ,D、E分别是CC1和A1B的中点,AC=AA1=2
(2)求二面角A-BD-C的大小(反三角表示)解:∵ ABC-A1B1C1是直棱柱,AC⊥BC,∴AC⊥侧面BB1C1C,作CM⊥BD于M,连结AM,则∠AMC就是所求二面角的平面角;在⊿ACM中,AC=2∴tan∠AMC=AC/CM=即所求为AC⊥CM,返回例题讲解3、如图在直三棱柱ABC-A1B1C1中,底面ABC是等腰Rt⊿,∠C=900 ,D、E分别是CC1和A1B的中点,AA1=2,若点E在平面ABD上的射影是⊿ABD的重心G.
(1)求A1B与平面ABD所成的角(用反三角表示);解:连结BG,由已知∠EBG就是所求的角,…… ……∴A1B与平面ABD所成的角为返回例题讲解3、如图在直三棱柱ABC-A1B1C1中,底面ABC是等腰Rt⊿,∠C=900 ,D、E分别是CC1和A1B的中点,AA1=2,若点E在平面ABD上的射影是⊿ABD的重心G.
(2)求点A1到平面AED的距离。方法A:作垂线法方法B:等体积法返回3、如图在直三棱柱ABC-A1B1C1中,底面ABC是等腰Rt⊿,∠C=900 ,D、E分别是CC1和A1B的中点,AA1=2,若点E在平面ABD上的射影是⊿ABD的重心G.
(2)求点A1到平面AED的距离。解A:由上题解知,DE⊥平面AA1B1B∴平面ADE⊥平面AA1B1B于AE在⊿A1AB1中,A1K=方法A:作垂线法返回3、如图在直三棱柱ABC-A1B1C1中,底面ABC是等腰Rt⊿,∠C=900 ,D、E分别是CC1和A1B的中点,AA1=2,若点E在平面ABD上的射影是⊿ABD的重心G.
(2)求点A1到平面AED的距离。解B:方法B:等体积法方法C:对象转换法返回例:如图,已知正三棱柱ABC-A1B1C1中,底面边长为a,侧棱长为 a, D是A1C1上一点.
(1)当 等于多少时,BC1//平面AB1D,
(2)若D是A1C1的中点,
求二面角A1-B1A-D的大小。返回解:(1)如图,连B1C交BC1于E,过E作EF//CA交BA1于F,则EF平行等于 AC,
又AC//A1C1,所以 EF//A1C1.取A1C1的中点D,连DF,则EF//DC1,EF=DC1,所以四边形EFDC1是平行四边形.故 EC1//DF.
又DF 平面AB1D,
EC1 //平面AB1D,
所以BC1//平面AB1D.返回(2)因为D是A1C1的中点,所以B1D⊥平面AA1C1C,所以平面AB1D⊥平面AA1C1C,过A1作A1G⊥AD交AD于G,则A1G⊥平面AB1D.过A1作A1H⊥AB1于H,连HG,则AB1⊥HG,所以∠A1HG是二面角A1-B1A-D的平面角.在Rt△AA1B中.
A1H=返回在Rt△AA1D中,
A1G=在Rt△A1HG中,sin∠A1HG= . 所以∠A1HG=45°, 即二面角A1-B1A-D的大小是45°.返回例:如图所示,在长方体ABCD-A1B1C1D1中,底面A1B1C1D1是正方形,过对角线AC1的一个截面是钝角为α的一个菱形AEC1F,求此截面与底面ABCD所成角φ的大小. 返回在Rt△AEH中,∠AEH= ,AH=HE·tan = a·tan , AC1=2AH= a·tan ,
= EF×AC1=a2tan ,
SABCD=a2, cosφ=
∴ φ=arccos(cot ).解:∠AEC1=α,设正方形AC1边长为a,则BD= a,且EF//BD,EF= a,EF⊥AC1,返回例:如图,在直三棱柱ABC-A1B1C1中,AB1⊥BC1,AB=CC1=a,BC=b,
(1)设E、F分别是AB1、BC1的
中点,求证:EF//平面ABC;
(2)求证:A1C1⊥AB;
(3)求B1到平面ABC1的距离. 返回(1)设E、F分别是AB1、BC1的中点,求证:EF//平面ABC;解:(1)分别取AB、BC的中点M、N,连EM、MN、NP,于是EM BB1,FN BB1,
从而EM FN,即四边形EFNM是平行四边形,
∴ EF//MN,而EF 平面ABC, MN 平面ABC,
∴ EF//平面ABC;返回(2)求证:A1C1⊥AB;(2)连A1B,∵ ABC-A1B1C1是直三棱柱,∴ AA1⊥AB,
又AB=CC1=AA1,∴ ABB1A1是正方形,从而AB1⊥BA1,
∵ AB1⊥BC1,∴ AB1⊥平面A1BC1,∴ A1C1⊥AB1,
而A1C1⊥AA1,∴ A1C1⊥平面ABB1A1,∴ A1C1⊥AB; 返回(3)求B1到平面ABC1的距离. (3)∵ A1B1//AB,∴ A1B1//平面ABC, 于是B1到平面ABC1的距离等于A1到平面ABC1的距离,
自A1作A1H⊥AC1于H,由(2)知 BA⊥平面ACC1A1, ∴ BA⊥A1H,于是A1H⊥平面ABC1,
在Rt△AA1C1中,AA1=CC1=a,返回此即B1到平面ABC1的距离。 返回在棱长为a的正方体ABCD-A1B1C1D1中,E、F分别是棱AB与BC的中点,(1)求二面角B-FB1-E的大小;(2)求点D到平面B1EF的距离;(3)在棱DD1上能否找一点M,使BM⊥平面EFB.若能,试确定点M的位置,若不能,请说明理由.【解题回顾】此题也可以作面B1EF的垂线与DD1相交,再
说明可以找到一点M满足条件.过程如下:先证明面B1BDD1
⊥面B1EF,且面B1BDD1∩面B1EF=B1G,在平面B1BDD1内作BM
⊥B1G,延长交直线DD1于M,由二平面垂直的性质可得:
BM⊥面B1EF,再通过△B1BG∽△BDM可得M是DD1的中点,
∴在棱上能找到一点M满足条件.
此题是一道探索性命题.往往可先通过对条件的分析,猜
想出命题的结论,然后再进行证明.返回M返回练习题BC返回返回返回返回返回(05,浙江)、如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
(Ⅰ)当k= 时,求直线PA与平面PBC所成角的大小
(Ⅱ) 当k取何值时,O在平面PBC内的射影恰好为△PBC的重心?返回 三棱锥P-ABC中,侧面PAC与底面ABC
垂直,PA=PB=PC=3,
(1)求证:AB ⊥ BC;
(2)设AB=BC= ,求AC与平面PBC所成
角的大小. (2004年全国文科试题)EF返回(Ⅰ)证明:面PAD⊥面PCD;
(Ⅱ)求AC与PB所成的角;
(Ⅲ)求面AMC与面BMC
所成二面角的大小。例1.(05,全国,18)已知四棱锥P-ABCD的底面为直角梯形,AB∥DC, 底面ABCD,且PA=AD=DC= AB=1,M是PB的中点。返回例3、如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
(Ⅰ)求证:AE⊥平面BCE;
(Ⅱ)求二面角B-AC-E的大小;
(Ⅲ)求点D到平面ACE的距离。返回如图,在四棱锥P—ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB= ,BC=1,PA=2,E为PD的中点.
(Ⅰ)求直线AC与PB所成角的余弦值;
(Ⅱ)在侧面PAB内找一点N,使NE⊥面PAC,并求出N点到AB和AP的距离.返回思想方法: 空间的距离主要指点面距、线面距和面面距,
而后两种的求解一般可转化为第一种,即线面距
及面面距都是通过转化最终转为求解点面距解决
而完成的。(转化的思想)
例如:
