立体几何基础知识回顾[上学期]
图片预览
文档简介
立体几何基础知识回顾
尚月如
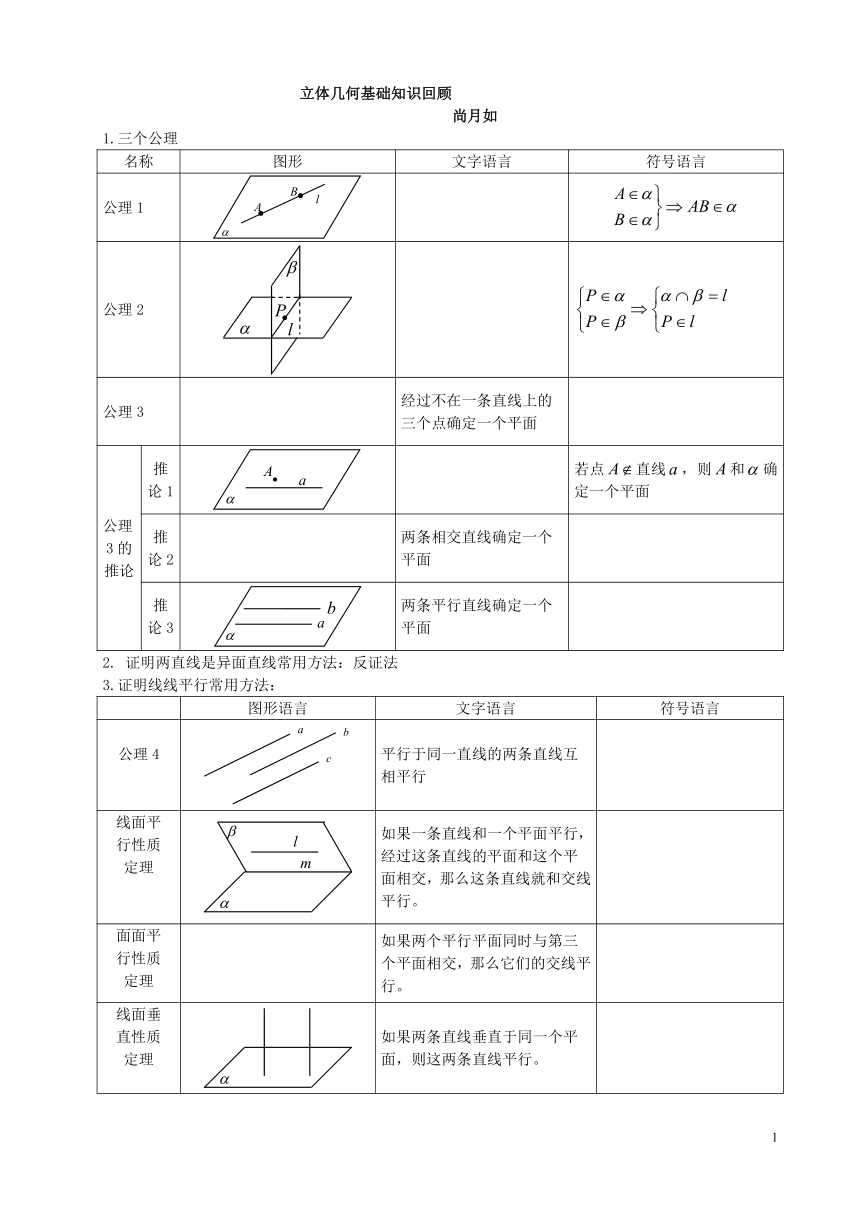
1.三个公理
名称 图形 文字语言 符号语言
公理1
公理2
公理3 经过不在一条直线上的三个点确定一个平面
公理3的推论 推论1 若点直线,则和确定一个平面
推论2 两条相交直线确定一个平面
推论3 两条平行直线确定一个平面
2. 证明两直线是异面直线常用方法:反证法
3.证明线线平行常用方法:
图形语言 文字语言 符号语言
公理4 平行于同一直线的两条直线互相平行
线面平行性质定理 如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行。
面面平行性质定理 如果两个平行平面同时与第三个平面相交,那么它们的交线平行。
线面垂直性质定理 如果两条直线垂直于同一个平面,则这两条直线平行。
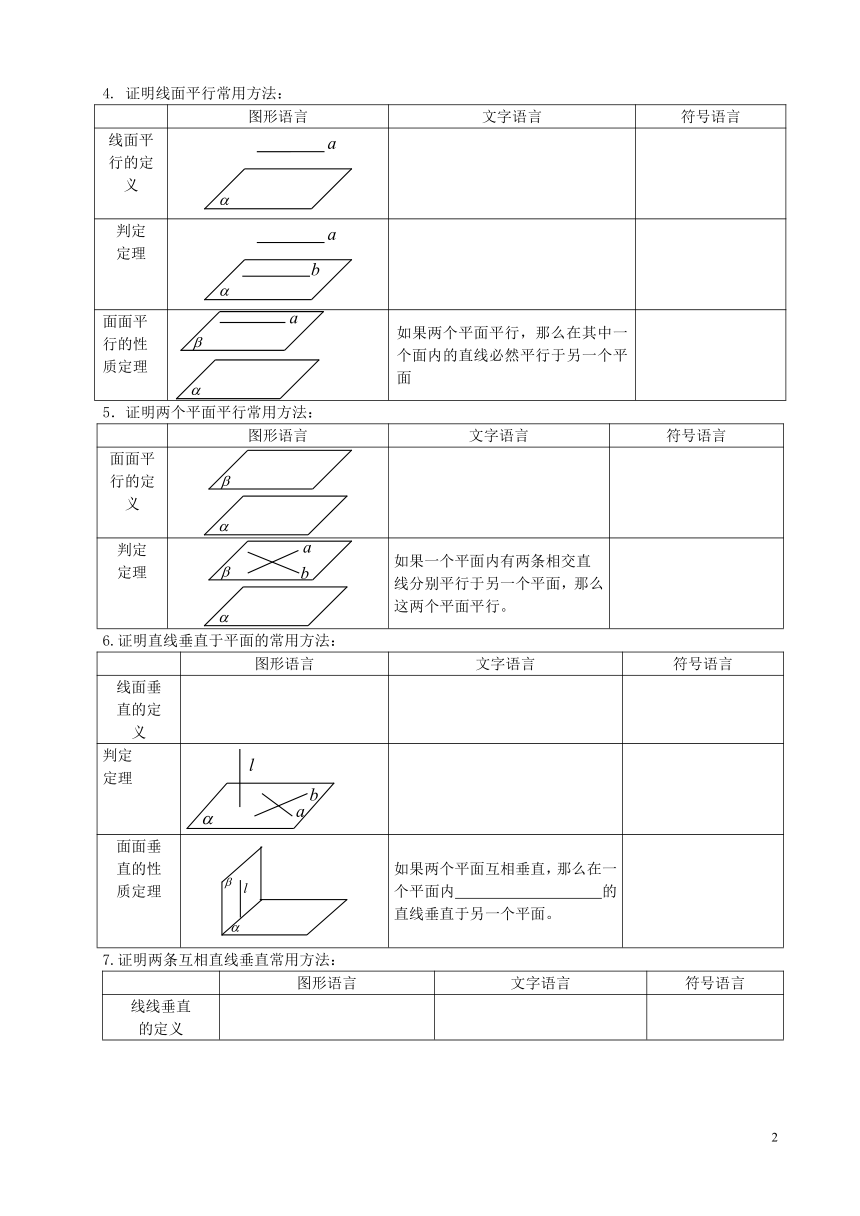
4. 证明线面平行常用方法:
图形语言 文字语言 符号语言
线面平行的定义
判定定理
面面平行的性质定理 如果两个平面平行,那么在其中一个面内的直线必然平行于另一个平面
5.证明两个平面平行常用方法:
图形语言 文字语言 符号语言
面面平行的定义
判定定理 如果一个平面内有两条相交直线分别平行于另一个平面,那么这两个平面平行。
6.证明直线垂直于平面的常用方法:
图形语言 文字语言 符号语言
线面垂直的定义
判定定理
面面垂直的性质定理 如果两个平面互相垂直,那么在一个平面内 的直线垂直于另一个平面。
7.证明两条互相直线垂直常用方法:
图形语言 文字语言 符号语言
线线垂直的定义
线面垂直的性质 如果一条直线和一个平面垂直,那么平面内的任何一条直线都和这条直线垂直。
8.证明两个平面互相垂直常用方法:
图形语言 文字语言 符号语言
两个平面垂直的定义
判定定理 如果一个平面经过另一个平面的 ,那么这两个平面互相 。
9.空间两条直线的位置关系是 ;
10.直线与平面的位置关系是 ;
11.平面与平面的位置关系是 。
12.两条异面直线所成角的取值范围是 ;
13.直线与平面所成角的取值范围是 ;
14.二面角的取值范围是 。
15.典型例题选讲
例1 已知平面α∥β,直线,且直线AB∥α,求证:AB∥β。
例2 已知正方体,是底对角线的交点.
求证:(1)C1O∥面;(2 )面.
例3已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是
AB、PC的中点.
(1) 求证:EF∥平面PAD;
(2) 求证:EF⊥CD;
(3) 若∠PDA=45°,求EF与平面ABCD所成的角的大小.
例4 如图,斜三棱柱ABC—A1B1C1中,AB=3,AC=2,AB⊥AC,A1C1⊥BC1侧棱与底面成600角,
(1)求证:AC⊥平面ABC1;
(2)求证:C1在平面ABC上的射影H在直线AB上;
例5如图,在棱长为1的正方体ABCD-A1B1C1D1中,E、F分别是面对角线BD和棱B1B上的任意一点.(1)求证:不论点E、F怎样移动,EF与A1C1所成的角均为定值;
(2)又若F为B1B的中点,当等于多少时,平面.
解:(1)在正方体ABCD-A1B1C1D1中,
即:不论点E、F怎样移动,EF与A1C1所成的角均为定值900.
(2)当时,平面.
连B1D1交A1C1于O1,连O1F,在,
由于,则,而,
又
平面
A
B
C
D
A1
B1
C1
D1
E
F
PAGE
1
尚月如
1.三个公理
名称 图形 文字语言 符号语言
公理1
公理2
公理3 经过不在一条直线上的三个点确定一个平面
公理3的推论 推论1 若点直线,则和确定一个平面
推论2 两条相交直线确定一个平面
推论3 两条平行直线确定一个平面
2. 证明两直线是异面直线常用方法:反证法
3.证明线线平行常用方法:
图形语言 文字语言 符号语言
公理4 平行于同一直线的两条直线互相平行
线面平行性质定理 如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行。
面面平行性质定理 如果两个平行平面同时与第三个平面相交,那么它们的交线平行。
线面垂直性质定理 如果两条直线垂直于同一个平面,则这两条直线平行。
4. 证明线面平行常用方法:
图形语言 文字语言 符号语言
线面平行的定义
判定定理
面面平行的性质定理 如果两个平面平行,那么在其中一个面内的直线必然平行于另一个平面
5.证明两个平面平行常用方法:
图形语言 文字语言 符号语言
面面平行的定义
判定定理 如果一个平面内有两条相交直线分别平行于另一个平面,那么这两个平面平行。
6.证明直线垂直于平面的常用方法:
图形语言 文字语言 符号语言
线面垂直的定义
判定定理
面面垂直的性质定理 如果两个平面互相垂直,那么在一个平面内 的直线垂直于另一个平面。
7.证明两条互相直线垂直常用方法:
图形语言 文字语言 符号语言
线线垂直的定义
线面垂直的性质 如果一条直线和一个平面垂直,那么平面内的任何一条直线都和这条直线垂直。
8.证明两个平面互相垂直常用方法:
图形语言 文字语言 符号语言
两个平面垂直的定义
判定定理 如果一个平面经过另一个平面的 ,那么这两个平面互相 。
9.空间两条直线的位置关系是 ;
10.直线与平面的位置关系是 ;
11.平面与平面的位置关系是 。
12.两条异面直线所成角的取值范围是 ;
13.直线与平面所成角的取值范围是 ;
14.二面角的取值范围是 。
15.典型例题选讲
例1 已知平面α∥β,直线,且直线AB∥α,求证:AB∥β。
例2 已知正方体,是底对角线的交点.
求证:(1)C1O∥面;(2 )面.
例3已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是
AB、PC的中点.
(1) 求证:EF∥平面PAD;
(2) 求证:EF⊥CD;
(3) 若∠PDA=45°,求EF与平面ABCD所成的角的大小.
例4 如图,斜三棱柱ABC—A1B1C1中,AB=3,AC=2,AB⊥AC,A1C1⊥BC1侧棱与底面成600角,
(1)求证:AC⊥平面ABC1;
(2)求证:C1在平面ABC上的射影H在直线AB上;
例5如图,在棱长为1的正方体ABCD-A1B1C1D1中,E、F分别是面对角线BD和棱B1B上的任意一点.(1)求证:不论点E、F怎样移动,EF与A1C1所成的角均为定值;
(2)又若F为B1B的中点,当等于多少时,平面.
解:(1)在正方体ABCD-A1B1C1D1中,
即:不论点E、F怎样移动,EF与A1C1所成的角均为定值900.
(2)当时,平面.
连B1D1交A1C1于O1,连O1F,在,
由于,则,而,
又
平面
A
B
C
D
A1
B1
C1
D1
E
F
PAGE
1
