利用典型立体几何模型[下学期]
图片预览



文档简介
立体几何复习方法
利用典型立体几何模型
复习立体几何
要有准确的空间想象能力,有看图、画图、理解图能力,同时具有必要的逻辑推理能力,运算能力.
利用典型的空间模型复习立体几何
典型的空间模型就是典型的空间环境,利用典型的空间模型可以很顺利地解决高考中大型的立体几何题.
立体几何的概念、法则、定理都是在一定的“几何环境”中形成的,我们把它叫做几何环境,典型的空间模型就是典型的几何环境,许多同学对典型的几何环境理解地不深,他们把它当做佷一般的一道题解,所以在高考出现了很多很多与典型空间模型相关的甚至很难的大型立体几何题的时候,他们也感觉到上不去手.
下面的例题在高考中学生做得并不顺利,其原因就是典型的空间模型认识不足,利用典型的空间模型、熟悉几何环境意识不够.分几部分说:
一、长方体模型
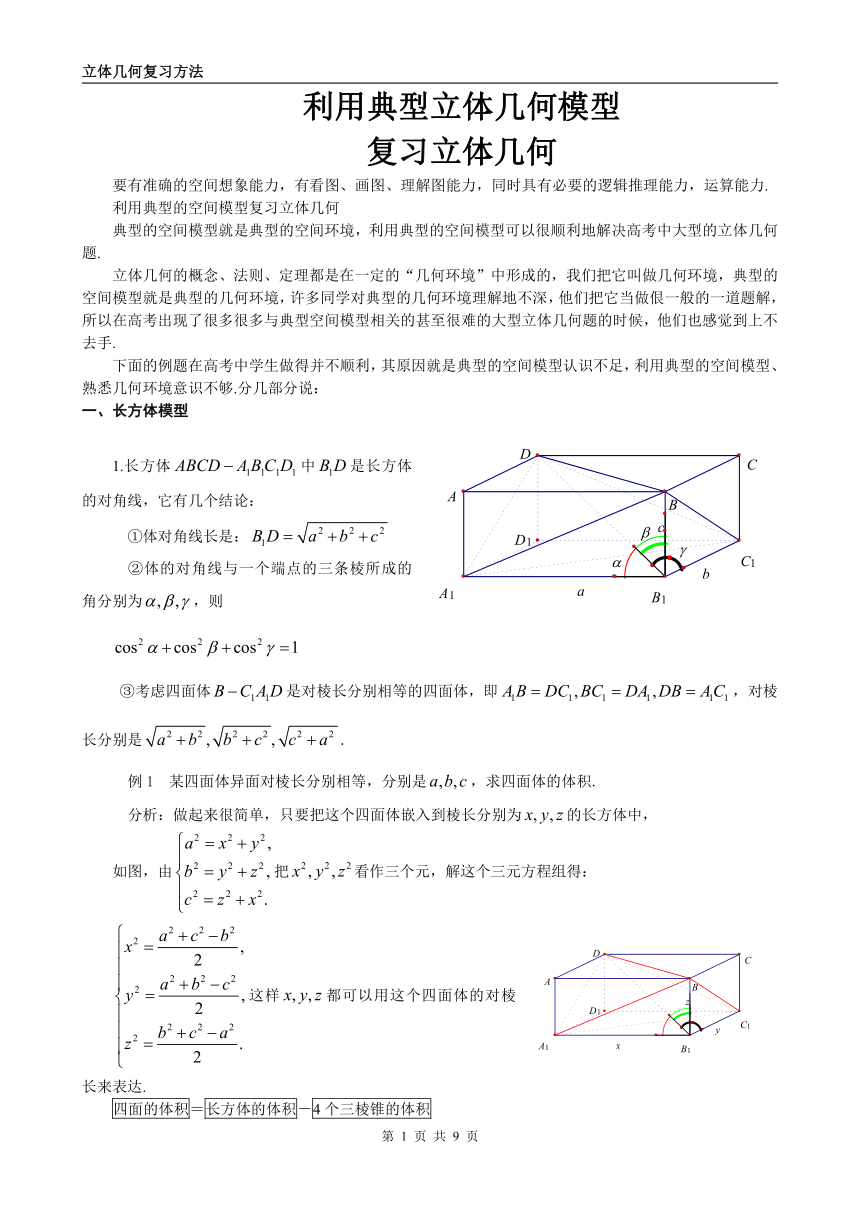
1.长方体中是长方体的对角线,它有几个结论:
①体对角线长是:
②体的对角线与一个端点的三条棱所成的角分别为,则
③考虑四面体是对棱长分别相等的四面体,即,对棱长分别是.
例1 某四面体异面对棱长分别相等,分别是,求四面体的体积.
分析:做起来很简单,只要把这个四面体嵌入到棱长分别为的长方体中,
如图,由把看作三个元,解这个三元方程组得:
这样都可以用这个四面体的对棱长来表达.
四面的体积=长方体的体积-4个三棱锥的体积
所以.
四面体中异面对棱长分别为的四面体的体积的算法——嵌入法.这种方法叫做嵌入法,“嵌入”的意思就是把不容易找到体积的空间图形放到能够嵌住的一个大的长方体,而那个大的长方体的体积是比较好求的.这就是长方体模型的一个利用.
例2 如图,三棱锥中,,在△内,,求的度数.
在三棱锥内部嵌入一个长方体,长方体的三个面与三棱锥的三个面是吻合的,这样PM是这个长方体的对角线.根据,可得,从而.如果在图中随便连MC,解△MPC那恐怕不是好办法.
这说明思路不同常常造成解题繁简相差是很大的.我们这个题比较成功的是把长方体嵌到三棱锥里面去,而这个三棱锥是一个大长方体的一个角,以PM为对角线的长方体嵌到三棱锥是完全可能的.
例3 四棱锥中,是矩形,
,求PC与BD的成角.
解:延长AB到E,使AB=BE,连结EP、EC
所以PC与BD成角为.
长方体模型对于确立起了很大的作用.
二、长方体的“一角”模型
在三棱锥中,,且.
①以P为公共点的三个面两两垂直;
②△ABC是锐角三角形
证明:设
△ABC中
.
所以为锐角,同理也为锐角.
③P在底面ABC的射影是△ABC的垂心
④三棱锥的高
设直线AH交BC于D点,由于H点一定在△ABC内部,所以D点一定在BC上,连结PD.
在△PAD中,
这个结果也可以这样说:如果在三棱锥中,在底面上作于D,连结PD,
则.或者说:作则.这将来对二面角的平面角有好的影响.
⑤的平面角分别是
.
⑤体积:;⑥它的外接球直径是.
例4 四棱锥中,底面是边长为的正方形,,求的大小.
考虑三棱锥,它就是模型2-长方体的“一个角”.本来我们可以利用…,这儿只要过A作AF,连结BF,于是.则就是二面角A-DE-B的平面角,只要把这个角算出就行.首先△BAF是直角三角形,原因是是直角.
在Rt△BAF中
所以.
我们看到象例4这样本来是高考中大题目,可是抓到了长方体“一角”,做起来就变得很轻松了.
例5 直二面角中,ABCD是边长为2的正方形(见图)AE=BE,F为CE上的点,BF⊥面ACE,求D到面ACE的距离.
这是一道高考中的大题.因为D-AB-E是直二面角,BC⊥面ABE,当然面ABCD⊥面ABE,又因为ABCD是正方形,BC要垂直于面ABE.
在ABE中,AE就是面内的一条线,而BE就是BF在该面内的射影,而AE是垂直于BF,这是因为BF垂直面ACE的,所以AE是垂直于面ACE的.所以AE垂直于BF,又有AE=BE,所以△ABE是等腰直角三角形.这一小段是熟悉几何环境的过程.图形中特殊的位置关系约束△ABE的形状.
补充图形,在正方体看问题.在这里看直二面角的局部图形.
问题就转化为:求D到面ACE的距离,就是求O点到面AB1C的距离.
因为O,B到面ACB1的距离相等,所以只须求B到面ACB1的距离即可,
考虑三棱锥B-ACB1,它是模型2.
所以,D到面ACE的距离为.
比起高考评分标准给的答案那要简单得多了.这儿要注意:一个是把局部的直二面角根据它的AEB是以E为直角的等腰直角三角形和ABCD是正方形的图形特征,补足正方体,这就是一种扩大的几何环境,而正方体也就是长方体模型,另一方面又抓到这正方体的一个角B-ACB1,那么这个角的模型更高,这就使我们在运算过程中得以简化.
所以说一道看起来很复杂的几何题,用典型几何模型做就显得轻松.
例6 底面为ABCD的长方体被截面AEC1F所截,AB=4,BC=2,CC1=3,BE=1(见图),求C点到面AEC1F的距离.
这也是一道高考题,在评分标准中给出了很多的辅助线.现在我们用典型的空间模型,再对这道题解解看.
解:延长C1E,交CB的延长线于M,延长CD,交C1F延长线于N,C-C1NM是模型2.
因为
同理.
所以,C到面C1MN的距离为
.
利用模型解法比高考试卷评分标准中答案要简单得多.
三、公式的几何模型
AB是PB在内的射影,BC是内一条直线则有.
大家要注意搞清楚那个是,那个是,那个是,实际上只要搞清那个是,另外两个就是.
内的直线不一定过B,如右图所示:
在直线AB上有一点D,过D在画一直线DC,则是直线PB与DC所成的角,则
那么这样的有可能利用这样的模型计算出异面直线成角.PB和DC的成角.
例7 EA⊥面ABCD,ABCD是边长为的正方形,EA=1,在AC上是否存在P点,使PE、BC成角.
即所以.
可见AC中点即是要找的点P
例8 长方体中,AB=2,AA1=1,BD与面AA1B1B成30°角.AE⊥BD于E,F为A1B1的中点,求AE,BF成角.
=
所以AE,BF成角为.
这样的一个题目,最重要的是位.在高考评分标准中,都要有很长的解题过程中.
这些结论在高考中,教材中有的可以直接用,有的可以先用,然后把结论来源说明.这样可以减少思考的时间与计算量.这就相当于电脑中的集成块一样,减少空间.
四、正四面体
正四面体如同平面几何中的正三角形,是立体几何中最常见的基础四面体,特别在多球问题中有广泛的应用.正四面体的主要数量特征都集中在它的对称面上.如图1,正四面体,E、F分别是对棱BC、AD的中点,△AED是它的对称面,若正四面体的棱长为1,通过解△AED,可得它的对棱距离.高,内切球半径,外接球的半径,表面积为,体积为,相邻面所成的角的平面角为,侧棱与底面成的角为.
例1 (05全国卷Ⅰ,理第5题)如图2,在多面体ABCDEF中,已知ABCD是边长为1的正方形,且△ADE、△BCF均为正三角形,EF//AB,EF=2,则该多面体的体积为( )
A. B. C. D.
多面体ABCDEF是由一个侧面为正方形ABCD的正三棱柱,与一个边长为1的正四面体组合而成.这个正三棱柱的侧棱与对面的距离(即EF与面ABCD的距离)等于正四面体的对棱距离,因此它的体积为,故选A.
例2 (05全国卷Ⅱ,理第12题)将半径都为1的4个小球完全装入正四面体的容器里,这个正四面体高的最小值为( )
A. B. C. D.
这四个小球放入后,它们的球心也形成了一个边长为2的正四面体,这个四面体与正四面体容器有公共的中心(内切球与外接球的公共球心),中心到各个面的距离是它的半径,而中心到两个正四面体的对应面的距离相差1,若四面体的边长为2,对应这个距离为,容器的中心到面的距离为,则容器的高是它的四倍,故应选C.
五、双垂四面体
如图3,四面体A-BCD,AB⊥面BCD,CD⊥面BCA,这种四面体构成许多简单多面体的基本图形,不妨称为双垂四面体,主要性质:
(1)它的四个面都是直角三角形;
(2);
(3)以BD、BC和AC为棱的二面角都是直二面角,以AB、BC为棱的二面角的平面角,分别是与;
(4)以AD为棱的二面角为,则;
(5)对棱AB与CD垂直,且BC是它们的公垂线;
(6)对棱AD与BC为异面直线,它们夹角为,则,等等.
例3 (05湖南卷,理第17题)如图4,ABCD是上下底长分别为2和6,高为的等腰梯形,将它沿对称轴OO1拆成直二面角,如图5.
(1)证明:AC⊥BO1;
(2)求二面角O-AC-O1的大小.
(1)略
(2)∵平面AOO1⊥平面OO1C,又∵AO⊥O1C,∴AO平面OO1C,同理CO1⊥平面AOO1,四面体AOO1C是一个双垂四面体,若二面角O-AC-O1的平面角为,则,根据条件,从图5中可知AO=3,OC=2,,CO1=1,即可自得.
例4 (05福建·第20题)如图6,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
(1)求证:AE⊥平面BCE;
(2)求二面角B-AC-E的大小;
(3)求点D到平面ACE的距离.
当(1)证明后,我们很容易识别四面体A-EBC是一个双垂四面体,若二面角B-AC-E的平面角为,则,由条件可以计算出AB=CB=2,AE=,,∴.
值得注意的是此题的(3)并不需要用等积变换,根据平面斜线上两点到平面的距离等于它们的斜线长的比,∴点D到平面ACE的距离等于B点到平面ACE的距离,也就是线段BF的长为
(05广东卷第16题 ) (本小题共14分)
如图3所示,在四面体中,已知,
.是线段上一点,,点在线段上,且.
(Ⅰ)证明:;
(Ⅱ)求二面角的大小.
【答案】
(Ⅰ)证明:在中, ∵
∴
∴△PAC是以∠PAC为直角的直角三角形,
同理可证,△PAB是以∠PAB为直角的直角三角形,
△PCB是以∠PCB为直角的直角三角形.
在中,∵
∴ ∴ 又∵
∴
(II)由(I)知PB⊥CE,PA⊥平面ABC
∴AB是PB在平面ABC上的射影,故AB⊥CE ∴CE⊥平面PAB,而EF平面PAB,
∴EF⊥EC, 故∠FEB是二面角B—CE—F的平面角,
∵ ∴,
∴二面角B—CE—F的大小为.
(05重庆第20题文)(本小题满分13分)
如图,在四棱锥P—ABCD中,底面ABCD为矩形,PD⊥底面ABCD,E是AB上一点,PE⊥EC. 已知求
(Ⅰ)异面直线PD与EC的距离;
(Ⅱ)二面角E—PC—D的大小.
(Ⅰ)因PD⊥底面,故PD⊥DE,又因EC⊥PE,且DE
是PE在面ABCD内的射影,由三垂直线定理的逆定理知
EC⊥DE,因此DE是异面直线PD与EC的公垂线.
设DE=x,因△DAE∽△CED,故(负根舍去).
从而DE=1,即异面直线PD与EC的距离为1.
(Ⅱ)过E作EG⊥CD交CD于G,作GH⊥PC交PC于H,连接EH. 因PD⊥底面,
故PD⊥EG,从而EG⊥面PCD.
因GH⊥PC,且GH是EH在面PDC内的射影,由三垂线定理知EH⊥PC.
因此∠EHG为二面角的平面角.
在面PDC中,PD=,CD=2,GC=
因△PDC∽△GHC,故,
又
故在
即二面角E—PC—D的大小为
(05重庆理第20题).(本小题满分13分)
如图,在三棱柱ABC—A1B1C1中,AB⊥侧面BB1C1C,E为棱CC1上异于C、C1的一点,EA⊥EB1,已知AB=,BB1=2,BC=1,∠BCC1=,求:
(Ⅰ)异面直线AB与EB1的距离;
(Ⅱ)二面角A—EB1—A1的平面角的正切值.
(Ⅰ)因AB⊥面BB1C1C,故AB⊥BE.
又EB1⊥EA,且EA在面BCC1B1内的射影为EB.
由三垂线定理的逆定理知EB1⊥BE,因此BE是异面直线
AB与EB1的公垂线,
在平行四边形BCC1B1中,设EB=x,则EB1=,
作BD⊥CC1,交CC1于D,则BD=BC·
在△BEB1中,由面积关系得.
(负根舍去)
解之得CE=2,故此时E与C1重合,由题意舍去.
因此x=1,即异面直线AB与EB1的距离为1.
(Ⅱ)过E作EG//B1A1,则GE⊥面BCC1B,故GE⊥EB1且GE在圆A1B1E内,
又已知AE⊥EB1
故∠AEG是二面角A—EB1—A1的平面角.
因EG//B1A1//BA,∠AEG=∠BAE,故
(05天津第12题)若图,平面,且则异面直线PB与AC所成角的正切值等于__________。
A
D
A
E
A
图1
图2
A
C
B
P
F
E
图3
第 10 页 共 10 页
利用典型立体几何模型
复习立体几何
要有准确的空间想象能力,有看图、画图、理解图能力,同时具有必要的逻辑推理能力,运算能力.
利用典型的空间模型复习立体几何
典型的空间模型就是典型的空间环境,利用典型的空间模型可以很顺利地解决高考中大型的立体几何题.
立体几何的概念、法则、定理都是在一定的“几何环境”中形成的,我们把它叫做几何环境,典型的空间模型就是典型的几何环境,许多同学对典型的几何环境理解地不深,他们把它当做佷一般的一道题解,所以在高考出现了很多很多与典型空间模型相关的甚至很难的大型立体几何题的时候,他们也感觉到上不去手.
下面的例题在高考中学生做得并不顺利,其原因就是典型的空间模型认识不足,利用典型的空间模型、熟悉几何环境意识不够.分几部分说:
一、长方体模型
1.长方体中是长方体的对角线,它有几个结论:
①体对角线长是:
②体的对角线与一个端点的三条棱所成的角分别为,则
③考虑四面体是对棱长分别相等的四面体,即,对棱长分别是.
例1 某四面体异面对棱长分别相等,分别是,求四面体的体积.
分析:做起来很简单,只要把这个四面体嵌入到棱长分别为的长方体中,
如图,由把看作三个元,解这个三元方程组得:
这样都可以用这个四面体的对棱长来表达.
四面的体积=长方体的体积-4个三棱锥的体积
所以.
四面体中异面对棱长分别为的四面体的体积的算法——嵌入法.这种方法叫做嵌入法,“嵌入”的意思就是把不容易找到体积的空间图形放到能够嵌住的一个大的长方体,而那个大的长方体的体积是比较好求的.这就是长方体模型的一个利用.
例2 如图,三棱锥中,,在△内,,求的度数.
在三棱锥内部嵌入一个长方体,长方体的三个面与三棱锥的三个面是吻合的,这样PM是这个长方体的对角线.根据,可得,从而.如果在图中随便连MC,解△MPC那恐怕不是好办法.
这说明思路不同常常造成解题繁简相差是很大的.我们这个题比较成功的是把长方体嵌到三棱锥里面去,而这个三棱锥是一个大长方体的一个角,以PM为对角线的长方体嵌到三棱锥是完全可能的.
例3 四棱锥中,是矩形,
,求PC与BD的成角.
解:延长AB到E,使AB=BE,连结EP、EC
所以PC与BD成角为.
长方体模型对于确立起了很大的作用.
二、长方体的“一角”模型
在三棱锥中,,且.
①以P为公共点的三个面两两垂直;
②△ABC是锐角三角形
证明:设
△ABC中
.
所以为锐角,同理也为锐角.
③P在底面ABC的射影是△ABC的垂心
④三棱锥的高
设直线AH交BC于D点,由于H点一定在△ABC内部,所以D点一定在BC上,连结PD.
在△PAD中,
这个结果也可以这样说:如果在三棱锥中,在底面上作于D,连结PD,
则.或者说:作则.这将来对二面角的平面角有好的影响.
⑤的平面角分别是
.
⑤体积:;⑥它的外接球直径是.
例4 四棱锥中,底面是边长为的正方形,,求的大小.
考虑三棱锥,它就是模型2-长方体的“一个角”.本来我们可以利用…,这儿只要过A作AF,连结BF,于是.则就是二面角A-DE-B的平面角,只要把这个角算出就行.首先△BAF是直角三角形,原因是是直角.
在Rt△BAF中
所以.
我们看到象例4这样本来是高考中大题目,可是抓到了长方体“一角”,做起来就变得很轻松了.
例5 直二面角中,ABCD是边长为2的正方形(见图)AE=BE,F为CE上的点,BF⊥面ACE,求D到面ACE的距离.
这是一道高考中的大题.因为D-AB-E是直二面角,BC⊥面ABE,当然面ABCD⊥面ABE,又因为ABCD是正方形,BC要垂直于面ABE.
在ABE中,AE就是面内的一条线,而BE就是BF在该面内的射影,而AE是垂直于BF,这是因为BF垂直面ACE的,所以AE是垂直于面ACE的.所以AE垂直于BF,又有AE=BE,所以△ABE是等腰直角三角形.这一小段是熟悉几何环境的过程.图形中特殊的位置关系约束△ABE的形状.
补充图形,在正方体看问题.在这里看直二面角的局部图形.
问题就转化为:求D到面ACE的距离,就是求O点到面AB1C的距离.
因为O,B到面ACB1的距离相等,所以只须求B到面ACB1的距离即可,
考虑三棱锥B-ACB1,它是模型2.
所以,D到面ACE的距离为.
比起高考评分标准给的答案那要简单得多了.这儿要注意:一个是把局部的直二面角根据它的AEB是以E为直角的等腰直角三角形和ABCD是正方形的图形特征,补足正方体,这就是一种扩大的几何环境,而正方体也就是长方体模型,另一方面又抓到这正方体的一个角B-ACB1,那么这个角的模型更高,这就使我们在运算过程中得以简化.
所以说一道看起来很复杂的几何题,用典型几何模型做就显得轻松.
例6 底面为ABCD的长方体被截面AEC1F所截,AB=4,BC=2,CC1=3,BE=1(见图),求C点到面AEC1F的距离.
这也是一道高考题,在评分标准中给出了很多的辅助线.现在我们用典型的空间模型,再对这道题解解看.
解:延长C1E,交CB的延长线于M,延长CD,交C1F延长线于N,C-C1NM是模型2.
因为
同理.
所以,C到面C1MN的距离为
.
利用模型解法比高考试卷评分标准中答案要简单得多.
三、公式的几何模型
AB是PB在内的射影,BC是内一条直线则有.
大家要注意搞清楚那个是,那个是,那个是,实际上只要搞清那个是,另外两个就是.
内的直线不一定过B,如右图所示:
在直线AB上有一点D,过D在画一直线DC,则是直线PB与DC所成的角,则
那么这样的有可能利用这样的模型计算出异面直线成角.PB和DC的成角.
例7 EA⊥面ABCD,ABCD是边长为的正方形,EA=1,在AC上是否存在P点,使PE、BC成角.
即所以.
可见AC中点即是要找的点P
例8 长方体中,AB=2,AA1=1,BD与面AA1B1B成30°角.AE⊥BD于E,F为A1B1的中点,求AE,BF成角.
=
所以AE,BF成角为.
这样的一个题目,最重要的是位.在高考评分标准中,都要有很长的解题过程中.
这些结论在高考中,教材中有的可以直接用,有的可以先用,然后把结论来源说明.这样可以减少思考的时间与计算量.这就相当于电脑中的集成块一样,减少空间.
四、正四面体
正四面体如同平面几何中的正三角形,是立体几何中最常见的基础四面体,特别在多球问题中有广泛的应用.正四面体的主要数量特征都集中在它的对称面上.如图1,正四面体,E、F分别是对棱BC、AD的中点,△AED是它的对称面,若正四面体的棱长为1,通过解△AED,可得它的对棱距离.高,内切球半径,外接球的半径,表面积为,体积为,相邻面所成的角的平面角为,侧棱与底面成的角为.
例1 (05全国卷Ⅰ,理第5题)如图2,在多面体ABCDEF中,已知ABCD是边长为1的正方形,且△ADE、△BCF均为正三角形,EF//AB,EF=2,则该多面体的体积为( )
A. B. C. D.
多面体ABCDEF是由一个侧面为正方形ABCD的正三棱柱,与一个边长为1的正四面体组合而成.这个正三棱柱的侧棱与对面的距离(即EF与面ABCD的距离)等于正四面体的对棱距离,因此它的体积为,故选A.
例2 (05全国卷Ⅱ,理第12题)将半径都为1的4个小球完全装入正四面体的容器里,这个正四面体高的最小值为( )
A. B. C. D.
这四个小球放入后,它们的球心也形成了一个边长为2的正四面体,这个四面体与正四面体容器有公共的中心(内切球与外接球的公共球心),中心到各个面的距离是它的半径,而中心到两个正四面体的对应面的距离相差1,若四面体的边长为2,对应这个距离为,容器的中心到面的距离为,则容器的高是它的四倍,故应选C.
五、双垂四面体
如图3,四面体A-BCD,AB⊥面BCD,CD⊥面BCA,这种四面体构成许多简单多面体的基本图形,不妨称为双垂四面体,主要性质:
(1)它的四个面都是直角三角形;
(2);
(3)以BD、BC和AC为棱的二面角都是直二面角,以AB、BC为棱的二面角的平面角,分别是与;
(4)以AD为棱的二面角为,则;
(5)对棱AB与CD垂直,且BC是它们的公垂线;
(6)对棱AD与BC为异面直线,它们夹角为,则,等等.
例3 (05湖南卷,理第17题)如图4,ABCD是上下底长分别为2和6,高为的等腰梯形,将它沿对称轴OO1拆成直二面角,如图5.
(1)证明:AC⊥BO1;
(2)求二面角O-AC-O1的大小.
(1)略
(2)∵平面AOO1⊥平面OO1C,又∵AO⊥O1C,∴AO平面OO1C,同理CO1⊥平面AOO1,四面体AOO1C是一个双垂四面体,若二面角O-AC-O1的平面角为,则,根据条件,从图5中可知AO=3,OC=2,,CO1=1,即可自得.
例4 (05福建·第20题)如图6,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
(1)求证:AE⊥平面BCE;
(2)求二面角B-AC-E的大小;
(3)求点D到平面ACE的距离.
当(1)证明后,我们很容易识别四面体A-EBC是一个双垂四面体,若二面角B-AC-E的平面角为,则,由条件可以计算出AB=CB=2,AE=,,∴.
值得注意的是此题的(3)并不需要用等积变换,根据平面斜线上两点到平面的距离等于它们的斜线长的比,∴点D到平面ACE的距离等于B点到平面ACE的距离,也就是线段BF的长为
(05广东卷第16题 ) (本小题共14分)
如图3所示,在四面体中,已知,
.是线段上一点,,点在线段上,且.
(Ⅰ)证明:;
(Ⅱ)求二面角的大小.
【答案】
(Ⅰ)证明:在中, ∵
∴
∴△PAC是以∠PAC为直角的直角三角形,
同理可证,△PAB是以∠PAB为直角的直角三角形,
△PCB是以∠PCB为直角的直角三角形.
在中,∵
∴ ∴ 又∵
∴
(II)由(I)知PB⊥CE,PA⊥平面ABC
∴AB是PB在平面ABC上的射影,故AB⊥CE ∴CE⊥平面PAB,而EF平面PAB,
∴EF⊥EC, 故∠FEB是二面角B—CE—F的平面角,
∵ ∴,
∴二面角B—CE—F的大小为.
(05重庆第20题文)(本小题满分13分)
如图,在四棱锥P—ABCD中,底面ABCD为矩形,PD⊥底面ABCD,E是AB上一点,PE⊥EC. 已知求
(Ⅰ)异面直线PD与EC的距离;
(Ⅱ)二面角E—PC—D的大小.
(Ⅰ)因PD⊥底面,故PD⊥DE,又因EC⊥PE,且DE
是PE在面ABCD内的射影,由三垂直线定理的逆定理知
EC⊥DE,因此DE是异面直线PD与EC的公垂线.
设DE=x,因△DAE∽△CED,故(负根舍去).
从而DE=1,即异面直线PD与EC的距离为1.
(Ⅱ)过E作EG⊥CD交CD于G,作GH⊥PC交PC于H,连接EH. 因PD⊥底面,
故PD⊥EG,从而EG⊥面PCD.
因GH⊥PC,且GH是EH在面PDC内的射影,由三垂线定理知EH⊥PC.
因此∠EHG为二面角的平面角.
在面PDC中,PD=,CD=2,GC=
因△PDC∽△GHC,故,
又
故在
即二面角E—PC—D的大小为
(05重庆理第20题).(本小题满分13分)
如图,在三棱柱ABC—A1B1C1中,AB⊥侧面BB1C1C,E为棱CC1上异于C、C1的一点,EA⊥EB1,已知AB=,BB1=2,BC=1,∠BCC1=,求:
(Ⅰ)异面直线AB与EB1的距离;
(Ⅱ)二面角A—EB1—A1的平面角的正切值.
(Ⅰ)因AB⊥面BB1C1C,故AB⊥BE.
又EB1⊥EA,且EA在面BCC1B1内的射影为EB.
由三垂线定理的逆定理知EB1⊥BE,因此BE是异面直线
AB与EB1的公垂线,
在平行四边形BCC1B1中,设EB=x,则EB1=,
作BD⊥CC1,交CC1于D,则BD=BC·
在△BEB1中,由面积关系得.
(负根舍去)
解之得CE=2,故此时E与C1重合,由题意舍去.
因此x=1,即异面直线AB与EB1的距离为1.
(Ⅱ)过E作EG//B1A1,则GE⊥面BCC1B,故GE⊥EB1且GE在圆A1B1E内,
又已知AE⊥EB1
故∠AEG是二面角A—EB1—A1的平面角.
因EG//B1A1//BA,∠AEG=∠BAE,故
(05天津第12题)若图,平面,且则异面直线PB与AC所成角的正切值等于__________。
A
D
A
E
A
图1
图2
A
C
B
P
F
E
图3
第 10 页 共 10 页
