华师大版数学八年级下册17.2.1.2平面直角坐标系中的面积问题 课件(共16张PPT)
文档属性
| 名称 | 华师大版数学八年级下册17.2.1.2平面直角坐标系中的面积问题 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 644.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-09 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
17.2.1第二课时
平面直角坐标系中的面积问题
问题1
已知平面直角坐标系中,点A(1,-2),B(-4,-2),C(1,3).
则①线段AB与x轴的位置关系 ,线段AB的长度为 ;
②线段AC与y轴的位置关系 ,线段AC的长度为 。
平行
5
平行
5
平行x轴的直线上的AB两点间的距离为:AB=
平行y轴的直线上的AC两点间的距离为:AC=
问题2
求下列三角形的面积:
(1)A(1,4),B(0,0),C(4,0);
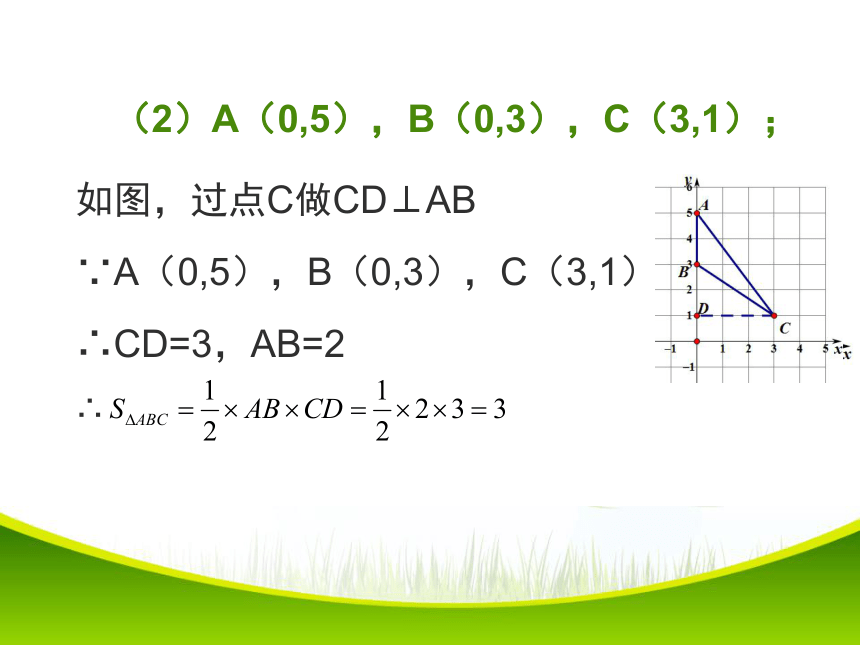
(2)A(0,5),B(0,3),C(3,1);
(1)A(1,4),B(0,0),C(4,0);
由图,过点A作AD⊥BC
∵A(1,4),B(0,0),C(4,0)
∴AD=4,BC=4
∴
(2)A(0,5),B(0,3),C(3,1);
如图,过点C做CD⊥AB
∵A(0,5),B(0,3),C(3,1)
∴CD=3,AB=2
∴
小结
平面直角坐标系中,求三角形的面积,关键在于找到平行x轴或平行y轴的线段作为规则图形的底和高。
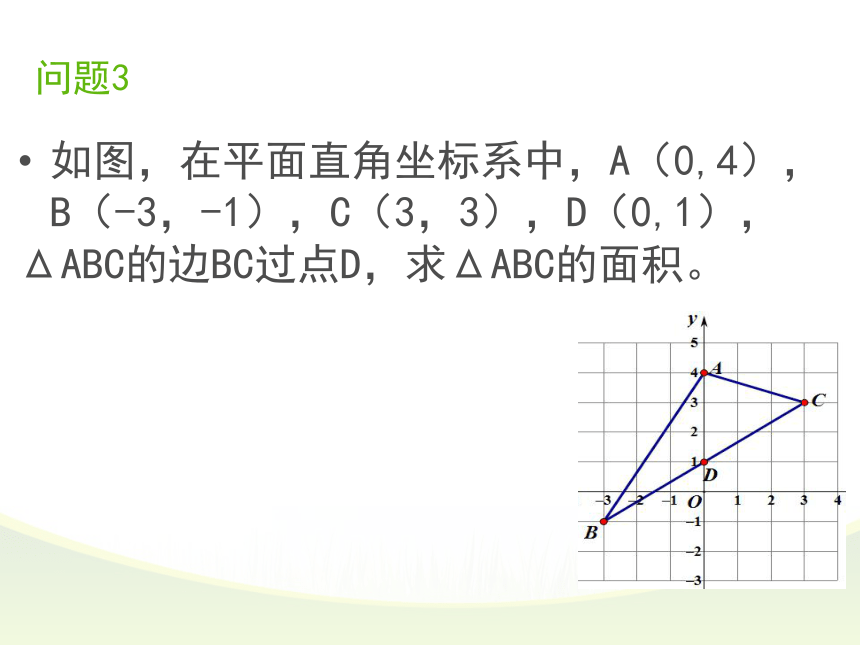
问题3
如图,在平面直角坐标系中,A(0,4),B(-3,-1),C(3,3),D(0,1),
ΔABC的边BC过点D,求ΔABC的面积。
方法一
将ΔABC补成如由图所示的长方形GEFB
方法二
将ΔABC补成如由图所示的直角梯形AEFB
方法三
∵A(0,4),D(0,1),且边BC过点D
∴AD=3,AD将ΔABC分割为ΔABD和ΔACD
分别过B、C作y轴的垂线BE,CF
∵B(-3,-1),C(3,3)
∴BE=3,CF=3
∴
F
E
补 补 割
F
E
问题4
在平面直角坐标系中,四边形OABC的顶点坐标分别为O(0,0),A(5,0),B(3,4),C(0,3),计算这个四边形的面积。
方法总结
割 割 割 补 补
小结
平面直角坐标系中求多边形的面积,通常通过割补法将多边行转化为规则图形进行求解。
拓展探索
如图,已知长方形ABCO中,边AB=8,BC=4,以点O为原点,OA,OC所在的直线为y轴和x轴,建立直角坐标系.
(1)点A的坐标为(0,4),则B点坐标为 ,C点坐标为 ;
(2)当点P从C出发,以2单位/秒速度沿CO方向移动(不过O点),Q从原点O出发以1单位/秒速度沿OA方向移动(不过A点),P,Q同时出发,在移动过程中,四边形OPBQ的面积是否变化?若不变,求其值;若变化,求其变化范围.
(8,4)
(8,0)
连接OB
由题意,t秒时,OQ=t CP=2t
∴OP=8-2t
∴
∴四边形OPBQ的面积不会发生改变
17.2.1第二课时
平面直角坐标系中的面积问题
问题1
已知平面直角坐标系中,点A(1,-2),B(-4,-2),C(1,3).
则①线段AB与x轴的位置关系 ,线段AB的长度为 ;
②线段AC与y轴的位置关系 ,线段AC的长度为 。
平行
5
平行
5
平行x轴的直线上的AB两点间的距离为:AB=
平行y轴的直线上的AC两点间的距离为:AC=
问题2
求下列三角形的面积:
(1)A(1,4),B(0,0),C(4,0);
(2)A(0,5),B(0,3),C(3,1);
(1)A(1,4),B(0,0),C(4,0);
由图,过点A作AD⊥BC
∵A(1,4),B(0,0),C(4,0)
∴AD=4,BC=4
∴
(2)A(0,5),B(0,3),C(3,1);
如图,过点C做CD⊥AB
∵A(0,5),B(0,3),C(3,1)
∴CD=3,AB=2
∴
小结
平面直角坐标系中,求三角形的面积,关键在于找到平行x轴或平行y轴的线段作为规则图形的底和高。
问题3
如图,在平面直角坐标系中,A(0,4),B(-3,-1),C(3,3),D(0,1),
ΔABC的边BC过点D,求ΔABC的面积。
方法一
将ΔABC补成如由图所示的长方形GEFB
方法二
将ΔABC补成如由图所示的直角梯形AEFB
方法三
∵A(0,4),D(0,1),且边BC过点D
∴AD=3,AD将ΔABC分割为ΔABD和ΔACD
分别过B、C作y轴的垂线BE,CF
∵B(-3,-1),C(3,3)
∴BE=3,CF=3
∴
F
E
补 补 割
F
E
问题4
在平面直角坐标系中,四边形OABC的顶点坐标分别为O(0,0),A(5,0),B(3,4),C(0,3),计算这个四边形的面积。
方法总结
割 割 割 补 补
小结
平面直角坐标系中求多边形的面积,通常通过割补法将多边行转化为规则图形进行求解。
拓展探索
如图,已知长方形ABCO中,边AB=8,BC=4,以点O为原点,OA,OC所在的直线为y轴和x轴,建立直角坐标系.
(1)点A的坐标为(0,4),则B点坐标为 ,C点坐标为 ;
(2)当点P从C出发,以2单位/秒速度沿CO方向移动(不过O点),Q从原点O出发以1单位/秒速度沿OA方向移动(不过A点),P,Q同时出发,在移动过程中,四边形OPBQ的面积是否变化?若不变,求其值;若变化,求其变化范围.
(8,4)
(8,0)
连接OB
由题意,t秒时,OQ=t CP=2t
∴OP=8-2t
∴
∴四边形OPBQ的面积不会发生改变
