华师大版数学八年级下册17.3.3一次函数的性质 课件(共13张PPT)
文档属性
| 名称 | 华师大版数学八年级下册17.3.3一次函数的性质 课件(共13张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-09 00:00:00 | ||
图片预览


文档简介
(共13张PPT)
八年级(下)
华师大版第17章 函数及其图象
温故知新
回忆:形如y=kx+b(k,b是常数,k≠0)的函数叫做一次函数。
如何求一次函数的图象与坐标轴的交点?
我们知道,函数反映了现实世界中量的变化规律,那么一次函数有什么性质呢?
情境激疑
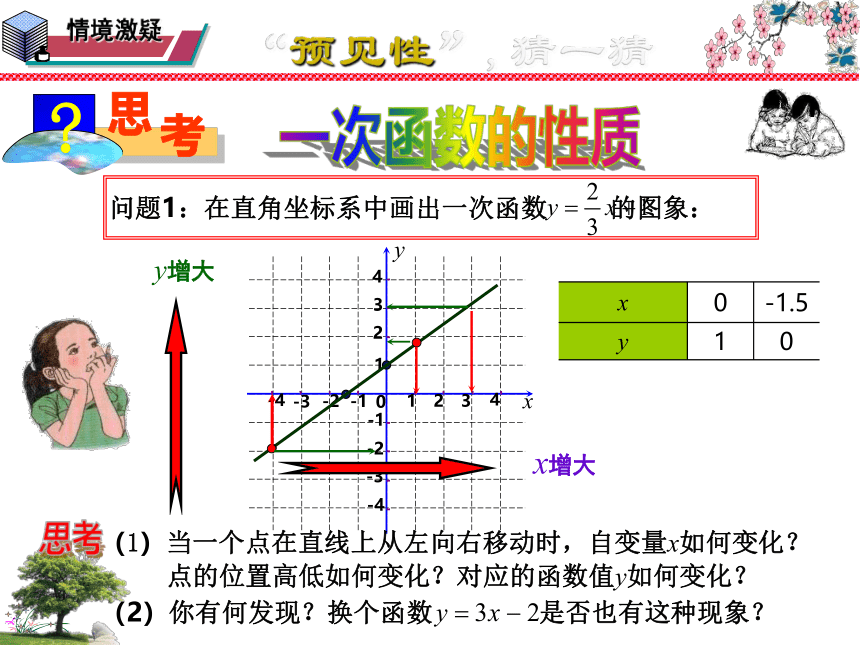
问题1:在直角坐标系中画出一次函数 的图象:
-1
-2
-3
1
2
3
4
4
3
0
2
1
-1
-2
-4
-3
-4
x 0 -1.5
y 1 0
(1)当一个点在直线上从左向右移动时,自变量x如何变化?
点的位置高低如何变化?对应的函数值y如何变化?
x增大
y增大
(2)你有何发现?换个函数 是否也有这种现象?
探究发现
x 0
y 0
1.5
-2
-1
-2
-3
1
2
3
4
4
3
0
2
1
-1
-2
-4
-3
-4
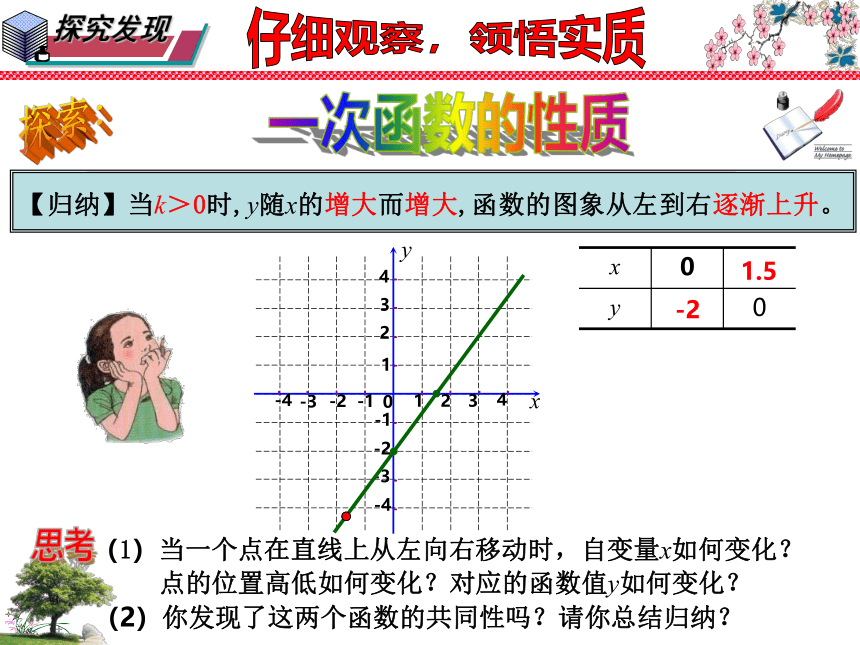
问题2:在直角坐标系中画出一次函数 的图象:
(1)当一个点在直线上从左向右移动时,自变量x如何变化?
点的位置高低如何变化?对应的函数值y如何变化?
(2)你发现了这两个函数的共同性吗?请你总结归纳?
【归纳】当k>0时,y随x的增大而增大,函数的图象从左到右逐渐上升。
探究发现
x 0
y 0
2
2
-1
-2
-3
1
2
3
4
4
3
0
2
1
-1
-2
-4
-3
-4
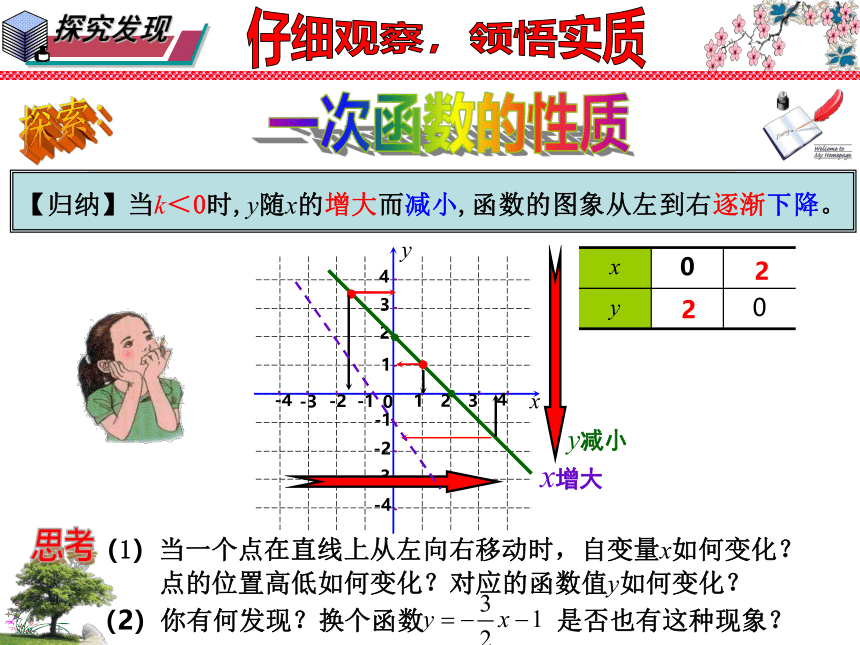
问题3:在直角坐标系中画出一次函数 的图象:
(1)当一个点在直线上从左向右移动时,自变量x如何变化?
点的位置高低如何变化?对应的函数值y如何变化?
x增大
y减小
(2)你有何发现?换个函数 是否也有这种现象?
【归纳】当k<0时,y随x的增大而减小,函数的图象从左到右逐渐下降。
要点解读
一次函数y=kx+b(k≠0)有下列性质:
(1)当k>0时,y随x的增大而增大,函数的图象从左到右逐渐上升;
(2)当k<0时,y随x的增大而减小,函数的图象从左到右逐渐下降;
(3)当b>0时,一次函数的图象与y交点在y轴正半轴(或x轴上方);
(4)当b<0时,一次函数的图象与y交点在y轴负半轴(或x轴下方).
(1)k决定一次函数y=kx+b图象的增减性和直线的倾斜方向;
(2)b决定一次函数y=kx+b图象与y轴的交点情况;
(3)一次函数的增减性对于正比例函数仍然适用,即增减性由k决定。
k 0,b 0
>
>
k 0,b 0
k 0,b 0
k 0,b 0
k 0,b 0
k 0,b 0
>
>
>
<
<
<
<
<
=
=
思考:根据一次函数的图象判断k,b的正负,并说出直线经过的象限:
学以致用
你是怎样考虑的…
解:(1)由题意得:
例 1
已知关于x的一次函数 ,回答下列问题:
(1)若y随x的增大而增大,且图象与y轴交点在x轴的上方,求m取值范围;
解得:
(2)若y随x的增大而减小,且图象与y轴交点在x轴的上方,求m取值范围。
(2)由题意得:
解得:
学以致用
你的解法是……
例 2
已知点(2,m),(-3,n)在直线 的图象上。试比较
m、n的大小,你能用几种方法呢?
数 学 活 动 室
学 以 致 用
1.已知点(-1,a)和( ,b)都在直线 上,试比较a和b大小.
已知点(-1,a)和( ,b)都在直线 上,并且a<b,求m的取值范围。
学以致用
例 3
画出函数 的图象,结合图象回答下列问题:
-1
-2
-3
1
2
3
4
4
3
O
2
1
-1
-2
-4
-3
-4
直线y=-2x+2
解:列表:
x 0
y=-2x+2 0
2
1
(1)随着x的增大,y将增大还是减小?图象从左到右怎样变化?
(2)当x取何值时,y=0;
(3)当x取何值时,y>0;
(4)当x取何值时,y<0.
学以致用
你的考虑是……
例 4
已知一次函数y=kx+b中自变量x的取值范围是-2≤x≤6,相应的函
数值是-11≤y≤9,求此函数的解析式。
【变式】已知一次函数y=kx+b(其中-1≤x≤2)的图象是一条线段,
且此线段两端点的纵坐标分别是1和4,求k和b的值。
我的收获是……
这节课我学到了什么?
我还有……的疑惑
小 结
八年级(下)
华师大版第17章 函数及其图象
温故知新
回忆:形如y=kx+b(k,b是常数,k≠0)的函数叫做一次函数。
如何求一次函数的图象与坐标轴的交点?
我们知道,函数反映了现实世界中量的变化规律,那么一次函数有什么性质呢?
情境激疑
问题1:在直角坐标系中画出一次函数 的图象:
-1
-2
-3
1
2
3
4
4
3
0
2
1
-1
-2
-4
-3
-4
x 0 -1.5
y 1 0
(1)当一个点在直线上从左向右移动时,自变量x如何变化?
点的位置高低如何变化?对应的函数值y如何变化?
x增大
y增大
(2)你有何发现?换个函数 是否也有这种现象?
探究发现
x 0
y 0
1.5
-2
-1
-2
-3
1
2
3
4
4
3
0
2
1
-1
-2
-4
-3
-4
问题2:在直角坐标系中画出一次函数 的图象:
(1)当一个点在直线上从左向右移动时,自变量x如何变化?
点的位置高低如何变化?对应的函数值y如何变化?
(2)你发现了这两个函数的共同性吗?请你总结归纳?
【归纳】当k>0时,y随x的增大而增大,函数的图象从左到右逐渐上升。
探究发现
x 0
y 0
2
2
-1
-2
-3
1
2
3
4
4
3
0
2
1
-1
-2
-4
-3
-4
问题3:在直角坐标系中画出一次函数 的图象:
(1)当一个点在直线上从左向右移动时,自变量x如何变化?
点的位置高低如何变化?对应的函数值y如何变化?
x增大
y减小
(2)你有何发现?换个函数 是否也有这种现象?
【归纳】当k<0时,y随x的增大而减小,函数的图象从左到右逐渐下降。
要点解读
一次函数y=kx+b(k≠0)有下列性质:
(1)当k>0时,y随x的增大而增大,函数的图象从左到右逐渐上升;
(2)当k<0时,y随x的增大而减小,函数的图象从左到右逐渐下降;
(3)当b>0时,一次函数的图象与y交点在y轴正半轴(或x轴上方);
(4)当b<0时,一次函数的图象与y交点在y轴负半轴(或x轴下方).
(1)k决定一次函数y=kx+b图象的增减性和直线的倾斜方向;
(2)b决定一次函数y=kx+b图象与y轴的交点情况;
(3)一次函数的增减性对于正比例函数仍然适用,即增减性由k决定。
k 0,b 0
>
>
k 0,b 0
k 0,b 0
k 0,b 0
k 0,b 0
k 0,b 0
>
>
>
<
<
<
<
<
=
=
思考:根据一次函数的图象判断k,b的正负,并说出直线经过的象限:
学以致用
你是怎样考虑的…
解:(1)由题意得:
例 1
已知关于x的一次函数 ,回答下列问题:
(1)若y随x的增大而增大,且图象与y轴交点在x轴的上方,求m取值范围;
解得:
(2)若y随x的增大而减小,且图象与y轴交点在x轴的上方,求m取值范围。
(2)由题意得:
解得:
学以致用
你的解法是……
例 2
已知点(2,m),(-3,n)在直线 的图象上。试比较
m、n的大小,你能用几种方法呢?
数 学 活 动 室
学 以 致 用
1.已知点(-1,a)和( ,b)都在直线 上,试比较a和b大小.
已知点(-1,a)和( ,b)都在直线 上,并且a<b,求m的取值范围。
学以致用
例 3
画出函数 的图象,结合图象回答下列问题:
-1
-2
-3
1
2
3
4
4
3
O
2
1
-1
-2
-4
-3
-4
直线y=-2x+2
解:列表:
x 0
y=-2x+2 0
2
1
(1)随着x的增大,y将增大还是减小?图象从左到右怎样变化?
(2)当x取何值时,y=0;
(3)当x取何值时,y>0;
(4)当x取何值时,y<0.
学以致用
你的考虑是……
例 4
已知一次函数y=kx+b中自变量x的取值范围是-2≤x≤6,相应的函
数值是-11≤y≤9,求此函数的解析式。
【变式】已知一次函数y=kx+b(其中-1≤x≤2)的图象是一条线段,
且此线段两端点的纵坐标分别是1和4,求k和b的值。
我的收获是……
这节课我学到了什么?
我还有……的疑惑
小 结
