华师大版数学八年级下册17.4.3反比例函数比例系数k的几何意义 课件(共14张PPT)
文档属性
| 名称 | 华师大版数学八年级下册17.4.3反比例函数比例系数k的几何意义 课件(共14张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-09 11:28:50 | ||
图片预览


文档简介
(共14张PPT)
八年级(下)
华师大版第17章 函数及其图象
温故知新
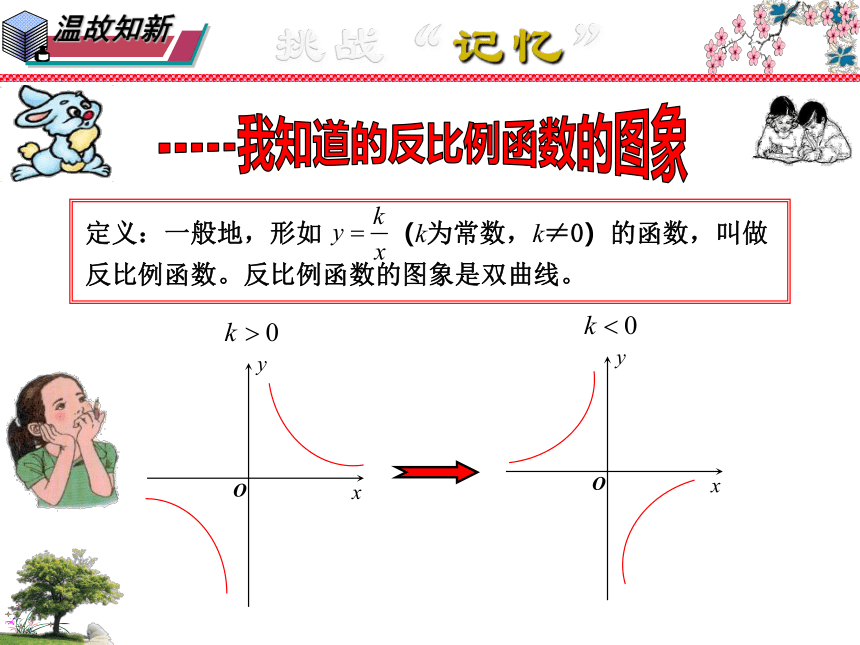
定义:一般地,形如 (k为常数,k≠0)的函数,叫做
反比例函数。反比例函数的图象是双曲线。
x
y
O
x
y
O
温故知新
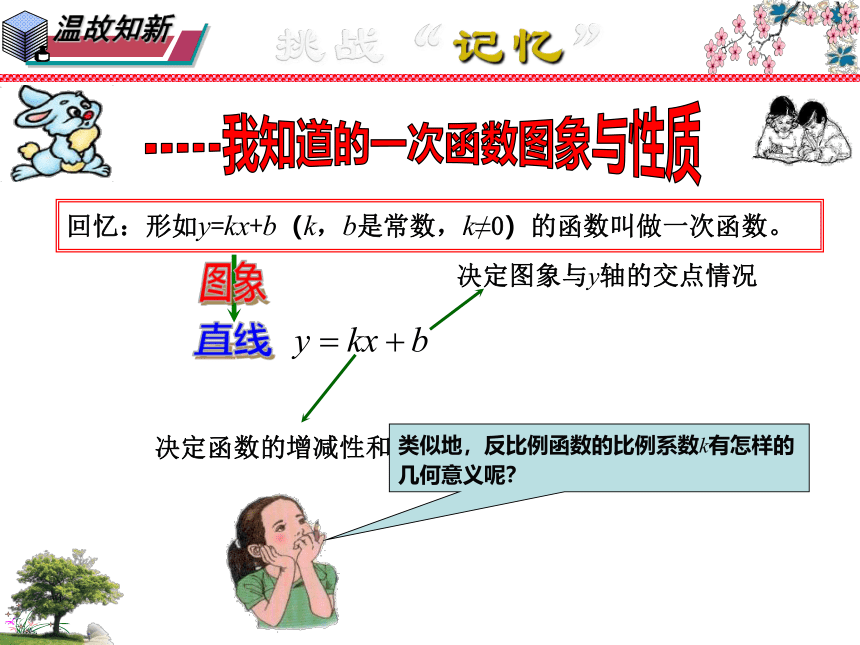
回忆:形如y=kx+b(k,b是常数,k≠0)的函数叫做一次函数。
决定函数的增减性和倾斜方向
决定图象与y轴的交点情况
类似地,反比例函数的比例系数k有怎样的几何意义呢?
探究发现
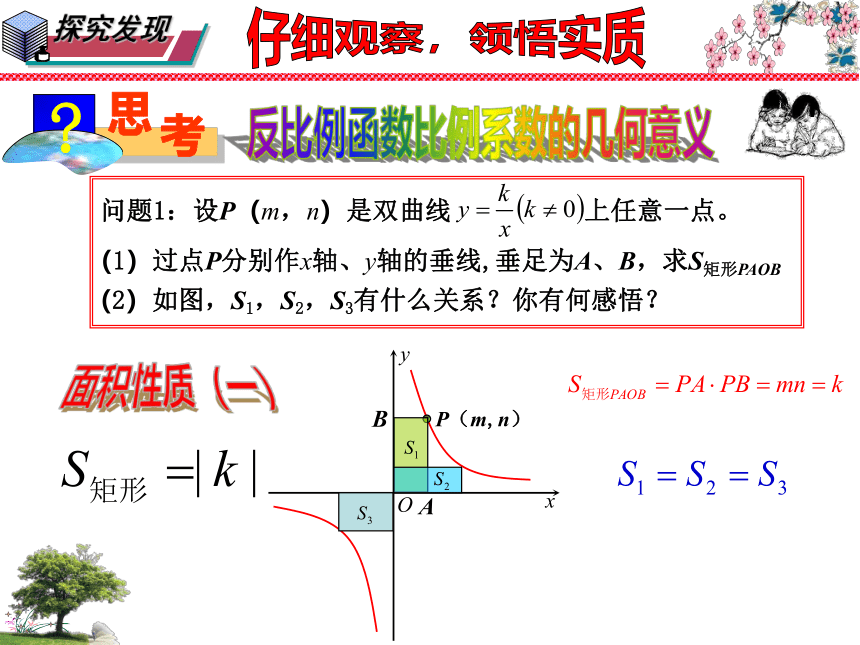
问题1:设P(m,n)是双曲线 上任意一点。
(1)过点P分别作x轴、y轴的垂线,垂足为A、B,求S矩形PAOB
y
O
x
P(m,n)
A
B
(2)如图,S1,S2,S3有什么关系?你有何感悟?
探究发现
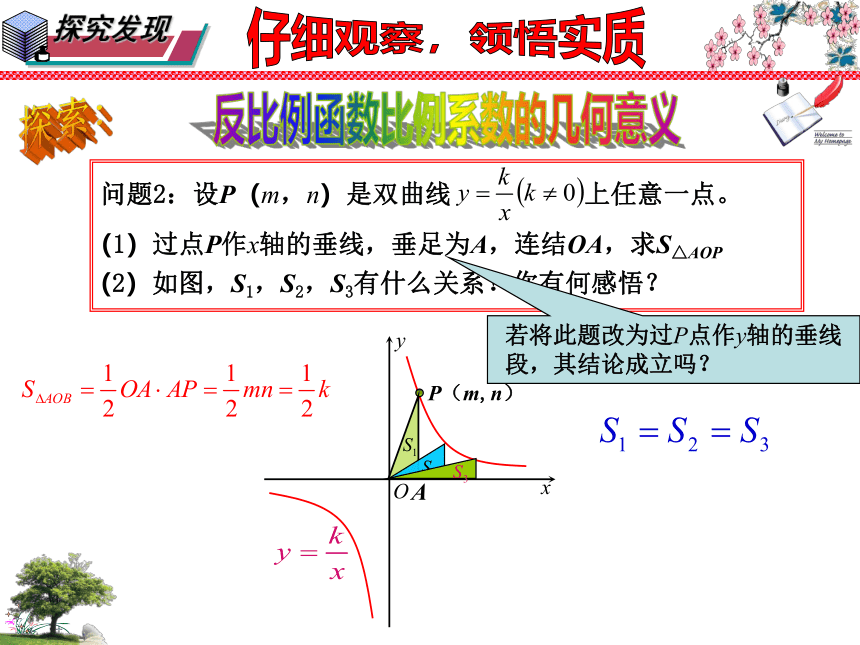
问题2:设P(m,n)是双曲线 上任意一点。
(1)过点P作x轴的垂线,垂足为A,连结OA,求S△AOP
(2)如图,S1,S2,S3有什么关系?你有何感悟?
y
O
x
P(m,n)
A
若将此题改为过P点作y轴的垂线段,其结论成立吗?
探究发现
P(m,n)
A
O
y
x
A
O
y
x
P(m,n)
学以致用
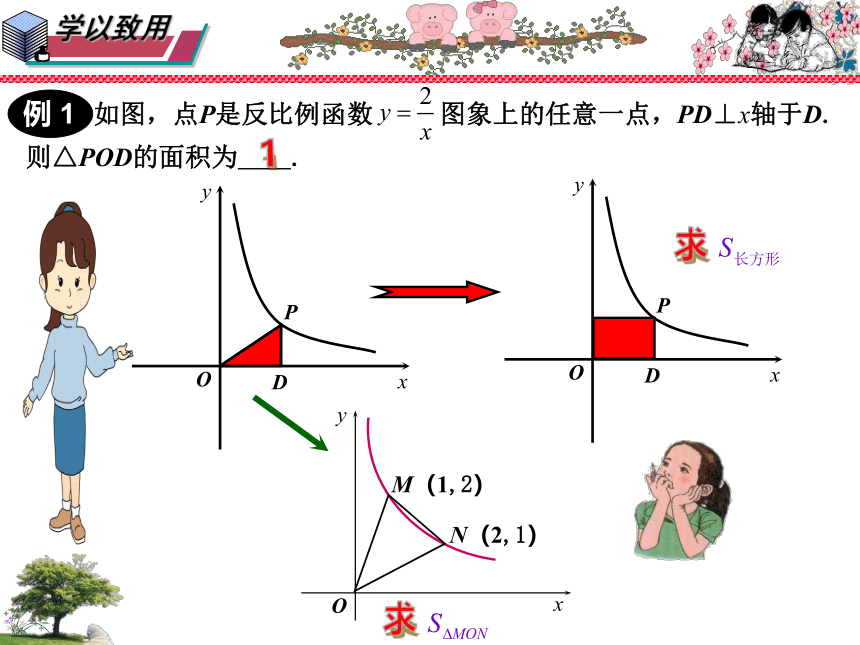
例 1
如图,点P是反比例函数 图象上的任意一点,PD⊥x轴于D.
则△POD的面积为 .
P
D
O
y
x
P
D
O
y
x
y
x
O
M(1,2)
N(2,1)
学以致用
例 2
如图,点P是反比例函数 的图象上任意一点,根据下列
条件,求k的值。
x
y
O
P
A
(1)若△PAO的面积为5,求k的值;
x
y
O
P
A
B
(2)若四边形PAOB的面积为5,求k的值。
数 学 活 动 室
学 以 致 用
1.如图所示的平面直角坐标系中,点P是反比例函数 图象上
的一点,PA⊥x轴于点A,则△POA的面积为 ;
x
y
O
P
A
2.如图,点P是反比例函数 图象上的一点,PA⊥y轴于点A,PB⊥x轴于点B,若矩形PBOA的面积为6,则k的值为 ;
x
y
O
P
B
A
学以致用
例 3
如图,点A、B是双曲线 上的点,分别经过A、B两点向x、y轴
作垂线段,若S阴影=0.5, .
y
x
O
y
x
O
1
2
3
4
学以致用
y
x
O
1
2
3
4
图形
变式
B2
O
x
y
P1
B1
A1
P2
A2
P3
B3
A3
A4
B4
P4
A5
B5
学以致用
例 4
如图,点A、点B分别在反比例函数 和 的图象上,且AB//x
轴,求△OAB的面积。
A
B
O
x
y
A
B
O
x
y
A
B
O
D
C
x
y
学以致用
争论
不休
x
y
B
P
D
A
C
O
例 5
如图,设点P在函数 的图象上,PC⊥x轴于点C,交函数
的图象于点A,PD⊥y轴于点D,交函数 的图象于点B,则四边形PAOB的面积为 .
我的收获是……
这节课我学到了什么?
我还有……的疑惑
小 结
八年级(下)
华师大版第17章 函数及其图象
温故知新
定义:一般地,形如 (k为常数,k≠0)的函数,叫做
反比例函数。反比例函数的图象是双曲线。
x
y
O
x
y
O
温故知新
回忆:形如y=kx+b(k,b是常数,k≠0)的函数叫做一次函数。
决定函数的增减性和倾斜方向
决定图象与y轴的交点情况
类似地,反比例函数的比例系数k有怎样的几何意义呢?
探究发现
问题1:设P(m,n)是双曲线 上任意一点。
(1)过点P分别作x轴、y轴的垂线,垂足为A、B,求S矩形PAOB
y
O
x
P(m,n)
A
B
(2)如图,S1,S2,S3有什么关系?你有何感悟?
探究发现
问题2:设P(m,n)是双曲线 上任意一点。
(1)过点P作x轴的垂线,垂足为A,连结OA,求S△AOP
(2)如图,S1,S2,S3有什么关系?你有何感悟?
y
O
x
P(m,n)
A
若将此题改为过P点作y轴的垂线段,其结论成立吗?
探究发现
P(m,n)
A
O
y
x
A
O
y
x
P(m,n)
学以致用
例 1
如图,点P是反比例函数 图象上的任意一点,PD⊥x轴于D.
则△POD的面积为 .
P
D
O
y
x
P
D
O
y
x
y
x
O
M(1,2)
N(2,1)
学以致用
例 2
如图,点P是反比例函数 的图象上任意一点,根据下列
条件,求k的值。
x
y
O
P
A
(1)若△PAO的面积为5,求k的值;
x
y
O
P
A
B
(2)若四边形PAOB的面积为5,求k的值。
数 学 活 动 室
学 以 致 用
1.如图所示的平面直角坐标系中,点P是反比例函数 图象上
的一点,PA⊥x轴于点A,则△POA的面积为 ;
x
y
O
P
A
2.如图,点P是反比例函数 图象上的一点,PA⊥y轴于点A,PB⊥x轴于点B,若矩形PBOA的面积为6,则k的值为 ;
x
y
O
P
B
A
学以致用
例 3
如图,点A、B是双曲线 上的点,分别经过A、B两点向x、y轴
作垂线段,若S阴影=0.5, .
y
x
O
y
x
O
1
2
3
4
学以致用
y
x
O
1
2
3
4
图形
变式
B2
O
x
y
P1
B1
A1
P2
A2
P3
B3
A3
A4
B4
P4
A5
B5
学以致用
例 4
如图,点A、点B分别在反比例函数 和 的图象上,且AB//x
轴,求△OAB的面积。
A
B
O
x
y
A
B
O
x
y
A
B
O
D
C
x
y
学以致用
争论
不休
x
y
B
P
D
A
C
O
例 5
如图,设点P在函数 的图象上,PC⊥x轴于点C,交函数
的图象于点A,PD⊥y轴于点D,交函数 的图象于点B,则四边形PAOB的面积为 .
我的收获是……
这节课我学到了什么?
我还有……的疑惑
小 结
