华师大版八年级下册19.2.2菱形判定--边的角度课件(共13张PPT)
文档属性
| 名称 | 华师大版八年级下册19.2.2菱形判定--边的角度课件(共13张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 899.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-09 12:17:01 | ||
图片预览




文档简介
(共13张PPT)
第2课时 从边的角度判定菱形
19.2 菱形
华师大版第19章 矩形、菱形与正方形
八年级(下)
数
学
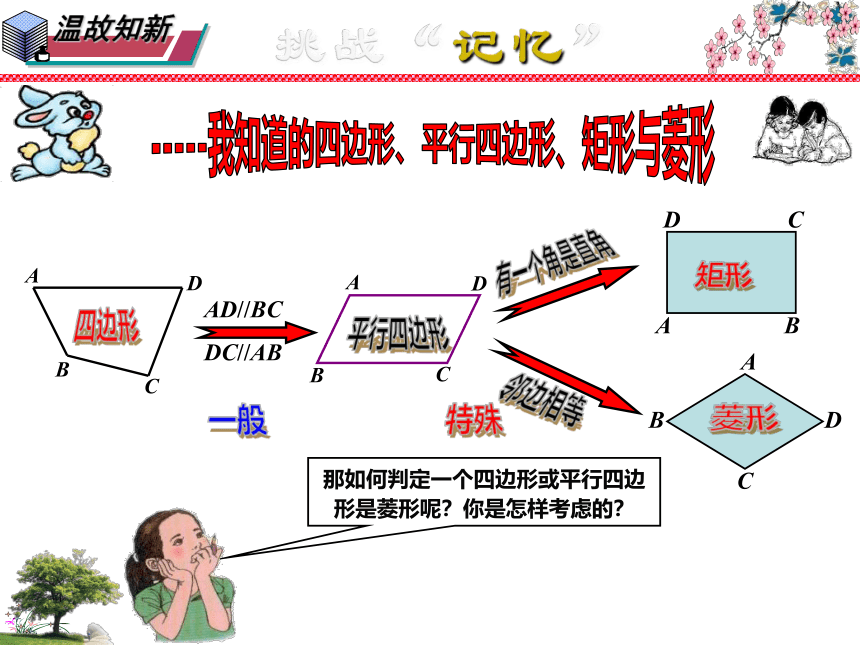
温故知新
-----我知道的四边形、平行四边形、矩形与菱形
平行四边形
A
B
C
D
四边形
A
B
C
D
AD//BC
DC//AB
一般
特殊
有一个角是直角
A
B
C
D
矩形
邻边相等
D
A
B
C
菱形
那如何判定一个四边形或平行四边形是菱形呢?你是怎样考虑的?
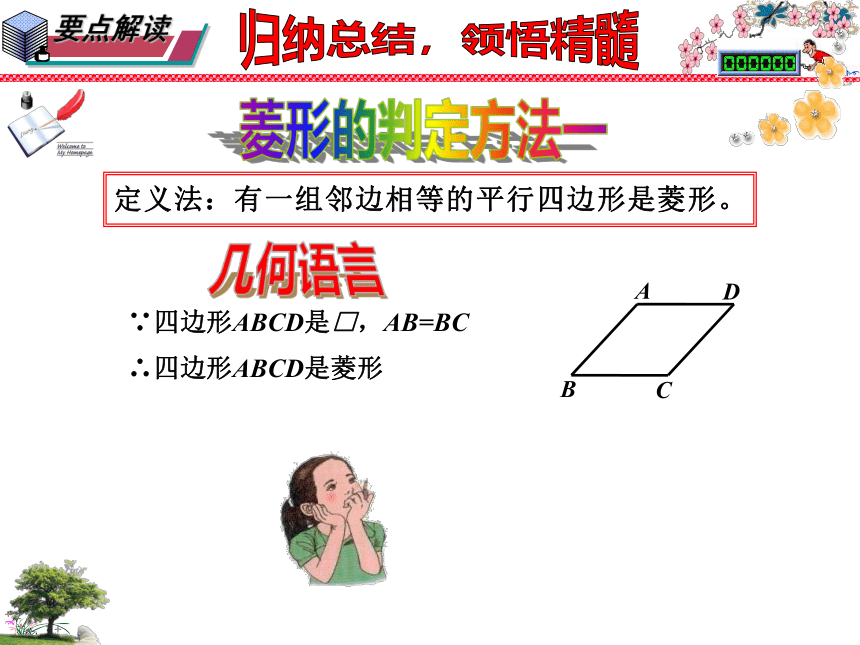
要点解读
归纳总结,领悟精髓
菱形的判定方法一
定义法:有一组邻边相等的平行四边形是菱形。
几何语言
∵四边形ABCD是□,AB=BC
∴四边形ABCD是菱形
B
A
C
D
学以致用
例 1
如图,在□ABCD中,AE⊥BC于E,AF⊥CD于F,且BE=DF.
(1)求证:△ABE≌△ADF;
(2)四边形ABCD是菱形吗?若是,请你证明。
【变式】如图,已知四边形是ABCD是平行四边形,E、F分别是AB、BC
上的点,AE=CF,∠AED=∠CFD.求证:
(1)△AED≌△CFD;
(2)四边形ABCD是菱形。
A
C
B
D
E
F
D
F
A
B
E
C
探究发现
思
考
仔细观察,领悟实质
问题:由菱形的性质“菱形的四条边都相等”,逆向思考,互换条件与结论,试写出它的逆命题。
菱形的判定
条件 结论
菱形的四条边都相等
逆命题
这是一个真命题吗?
四边形是菱形
四条边都相等
四条边都相等
四边形是菱形
探究发现
仔细观察,领悟实质
探索:
菱形的判定
观察你所作的图形,它是一个菱形吗?
思考
问题:请按下列步骤做一个四条边都相等的四边形。
步骤1:画两条相等的线段AB、AD;
步骤2:分别以点B和点D为圆心,AB长为半径画弧,两弧相交于点C;
步骤3:连结BC、CD.
即得到一个四条边都相等的四边形ABCD.
A
B
D
C
探究发现
探索:
仔细观察,领悟实质
菱形的判定
猜想:四条边都相等的四边形是菱形。
已知:四边形ABCD中,AB=BC=CD=AD
说明:四边形ABCD是菱形
思路解析
□ABCD
结论
四条边都相等的四边形是菱形。
AB=BC=CD=AD
AD=BC
AB=DC
AB=AD
B
A
C
D
□ABCD是菱形
菱形的判定方法二
结论
判定定理1:四条边相等的四边形是菱形。
几何语言
∵AB=BC=CD=AD
∴四边形ABCD是菱形
A
B
C
D
学以致用
例2
(1)求证:四边形EFGH是菱形;
(2)连结HF、EG,请问HF、EG有何关系?
如图,在矩形ABCD中,E、F、G、H分别是四边的中点。
A
D
B
C
E
F
G
H
(3)若AB=6,BC=8,求四边形EFGH的面积;
【变式】将上题中条件“E、F、G、H分别四边的中点”改变为“在正
方形 ABCD中,AH=BE=CF=DG”,判断四边形EFGH形状,并说明理由。
A
D
B
C
E
F
G
H
1.如图,在△ABC中, AD是角平分线,点E、F分别在AB、 AD上,且AE=AC,
EF = ED.求证:四边形CDEF是菱形.
练习巩固
2.已知:如图,AD平分∠BAC,DE∥AC 交AB于E,DF∥AB交AC于F.求证:四边形AEDF是菱形.
练习巩固
3..如图,在四边形ABCD中,AD//BC,AB=AD,∠BAD的平分
线AE交BD、BC于点G、E,连结DE。
(1)求证:四边形ABED是菱形;
(2)若ED⊥DC,∠ABC=60。,AB=2,求梯形ABCD的面积。
A
D
B
C
E
G
我的收获是……
这节课我学到了什么?
我还有……的疑惑
畅谈收获
小 结
第2课时 从边的角度判定菱形
19.2 菱形
华师大版第19章 矩形、菱形与正方形
八年级(下)
数
学
温故知新
-----我知道的四边形、平行四边形、矩形与菱形
平行四边形
A
B
C
D
四边形
A
B
C
D
AD//BC
DC//AB
一般
特殊
有一个角是直角
A
B
C
D
矩形
邻边相等
D
A
B
C
菱形
那如何判定一个四边形或平行四边形是菱形呢?你是怎样考虑的?
要点解读
归纳总结,领悟精髓
菱形的判定方法一
定义法:有一组邻边相等的平行四边形是菱形。
几何语言
∵四边形ABCD是□,AB=BC
∴四边形ABCD是菱形
B
A
C
D
学以致用
例 1
如图,在□ABCD中,AE⊥BC于E,AF⊥CD于F,且BE=DF.
(1)求证:△ABE≌△ADF;
(2)四边形ABCD是菱形吗?若是,请你证明。
【变式】如图,已知四边形是ABCD是平行四边形,E、F分别是AB、BC
上的点,AE=CF,∠AED=∠CFD.求证:
(1)△AED≌△CFD;
(2)四边形ABCD是菱形。
A
C
B
D
E
F
D
F
A
B
E
C
探究发现
思
考
仔细观察,领悟实质
问题:由菱形的性质“菱形的四条边都相等”,逆向思考,互换条件与结论,试写出它的逆命题。
菱形的判定
条件 结论
菱形的四条边都相等
逆命题
这是一个真命题吗?
四边形是菱形
四条边都相等
四条边都相等
四边形是菱形
探究发现
仔细观察,领悟实质
探索:
菱形的判定
观察你所作的图形,它是一个菱形吗?
思考
问题:请按下列步骤做一个四条边都相等的四边形。
步骤1:画两条相等的线段AB、AD;
步骤2:分别以点B和点D为圆心,AB长为半径画弧,两弧相交于点C;
步骤3:连结BC、CD.
即得到一个四条边都相等的四边形ABCD.
A
B
D
C
探究发现
探索:
仔细观察,领悟实质
菱形的判定
猜想:四条边都相等的四边形是菱形。
已知:四边形ABCD中,AB=BC=CD=AD
说明:四边形ABCD是菱形
思路解析
□ABCD
结论
四条边都相等的四边形是菱形。
AB=BC=CD=AD
AD=BC
AB=DC
AB=AD
B
A
C
D
□ABCD是菱形
菱形的判定方法二
结论
判定定理1:四条边相等的四边形是菱形。
几何语言
∵AB=BC=CD=AD
∴四边形ABCD是菱形
A
B
C
D
学以致用
例2
(1)求证:四边形EFGH是菱形;
(2)连结HF、EG,请问HF、EG有何关系?
如图,在矩形ABCD中,E、F、G、H分别是四边的中点。
A
D
B
C
E
F
G
H
(3)若AB=6,BC=8,求四边形EFGH的面积;
【变式】将上题中条件“E、F、G、H分别四边的中点”改变为“在正
方形 ABCD中,AH=BE=CF=DG”,判断四边形EFGH形状,并说明理由。
A
D
B
C
E
F
G
H
1.如图,在△ABC中, AD是角平分线,点E、F分别在AB、 AD上,且AE=AC,
EF = ED.求证:四边形CDEF是菱形.
练习巩固
2.已知:如图,AD平分∠BAC,DE∥AC 交AB于E,DF∥AB交AC于F.求证:四边形AEDF是菱形.
练习巩固
3..如图,在四边形ABCD中,AD//BC,AB=AD,∠BAD的平分
线AE交BD、BC于点G、E,连结DE。
(1)求证:四边形ABED是菱形;
(2)若ED⊥DC,∠ABC=60。,AB=2,求梯形ABCD的面积。
A
D
B
C
E
G
我的收获是……
这节课我学到了什么?
我还有……的疑惑
畅谈收获
小 结
