华师大版八年级下册19.3.2正方形(第2课时)课件((共11张PPT))
文档属性
| 名称 | 华师大版八年级下册19.3.2正方形(第2课时)课件((共11张PPT)) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-09 00:00:00 | ||
图片预览


文档简介
(共11张PPT)
华师大版第19章 矩形、菱形与正方形
八年级(下)
温故知新
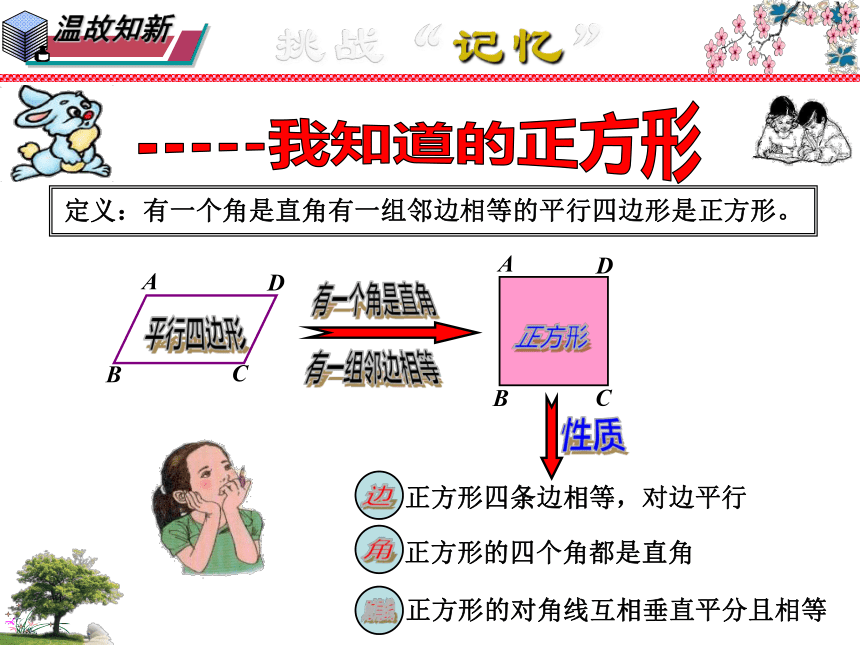
定义:有一个角是直角有一组邻边相等的平行四边形是正方形。
A
B
C
D
A
B
C
D
正方形的对角线互相垂直平分且相等
正方形四条边相等,对边平行
正方形的四个角都是直角
温故知新
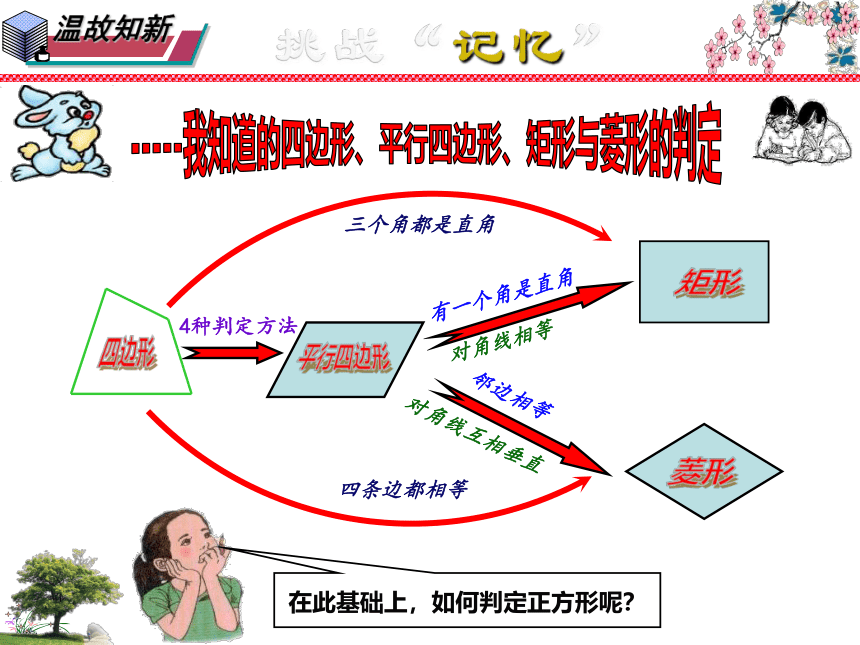
4种判定方法
邻边相等
有一个角是直角
对角线相等
对角线互相垂直
三个角都是直角
四条边都相等
在此基础上,如何判定正方形呢?
探究发现
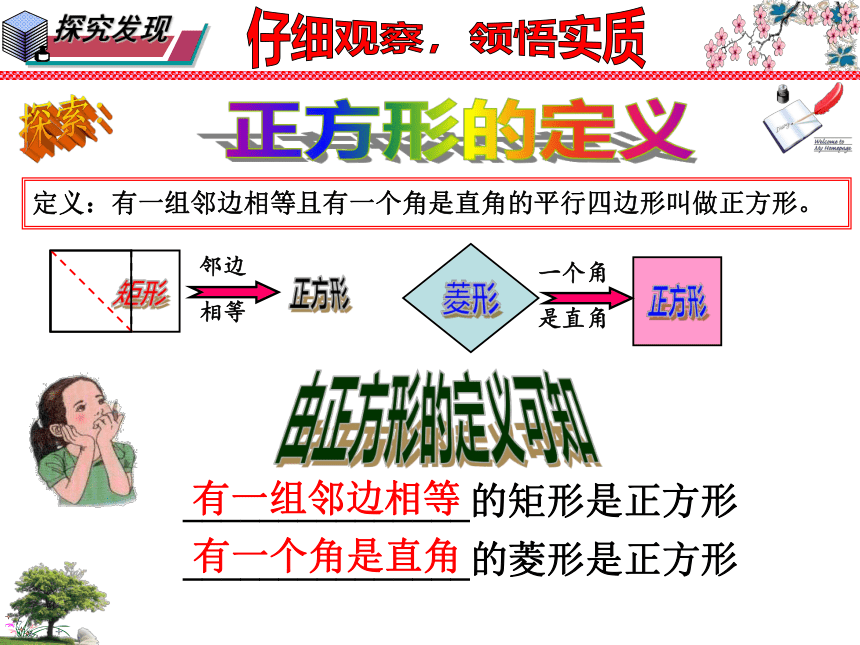
定义:有一组邻边相等且有一个角是直角的平行四边形叫做正方形。
_______________的矩形是正方形
邻边
相等
有一组邻边相等
_______________的菱形是正方形
一个角
是直角
有一个角是直角
要点解读
有一组邻边相等并且有一个角是直角的平行四边形是正方形。
既是矩形又是菱形(或者既是菱形又是矩形)的四边形是正方形。
(1)一组邻边相等的矩形是正方形;
(2)有一个角是直角的菱形是正方形。
要点解读
5种判定方法
邻边相等
有一个角是直角
对角线相等
对角线互相垂直
三个角都是直角
四条边都相等
邻边相等
有一个角是直角
学以致用
例 1
如图,在△ABC中,∠ACB=90°,CD平分∠ACB,DE ⊥BC于E,
DF ⊥AC于F,求证:四边形CFDE是正方形。
A
B
C
D
E
F
【变式】如图,在△ABC中,∠ACB=90°,∠CAB、 ∠ABC的平分线交
于点D,DE ⊥BC于E ,DF ⊥AC于F.求证:四边形CFDE是正方形。
A
B
C
D
F
E
G
学以致用
例 2
如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,AN是△ABC
外角∠CAM的平分线,CE⊥AN,垂足为D,连接DE交AC于点F.
(1)求证:四边形ADCE为矩形;
A
B
C
D
E
F
N
M
(2)当△ABC满足什么条件,四边形ADCE是一个正方形?并出证明;
(3) 在(2)的条件下,若AB=AC=2,求正方形ADCE的周长。
【变式】如图,在△ABC中,AB=AC,AD是△ABC的角平分线,点O为
AB的中点,连结DO并延长到点E,使OE=OD,连结AE,BE.
(1)求证:四边形AEBD为矩形;
(2)当△ABC满足什么条件,四边形AEBD是一个正方形?并出证明。
B
A
C
D
O
E
学以致用
例 3
如图所示,在△ABE中,D是BC边上的一动点(不与B、C重合),
DE//AC交AB于点E,DF//AB交AC于F.
(1)试探索AD满足什么条件时,四边形AEDF是菱形,并给出证明;
(2)在(1)的条件下, △ABC满足什么条件时,四边形AEDF是正方形.
A
B
C
D
E
F
数 学 活 动 室
学 以 致 用
如图,已知在□ABCD中,对角线AC,BD交于点O,E是BD的延长线上的点,且EA=EC.
(1)求证:四边形ABCD是菱形;
(2)若∠DAC=∠EAD+∠AED,求证:四边形ABCD是正方形。
A
B
C
D
E
O
我的收获是……
这节课我学到了什么?
我还有……的疑惑
小 结
华师大版第19章 矩形、菱形与正方形
八年级(下)
温故知新
定义:有一个角是直角有一组邻边相等的平行四边形是正方形。
A
B
C
D
A
B
C
D
正方形的对角线互相垂直平分且相等
正方形四条边相等,对边平行
正方形的四个角都是直角
温故知新
4种判定方法
邻边相等
有一个角是直角
对角线相等
对角线互相垂直
三个角都是直角
四条边都相等
在此基础上,如何判定正方形呢?
探究发现
定义:有一组邻边相等且有一个角是直角的平行四边形叫做正方形。
_______________的矩形是正方形
邻边
相等
有一组邻边相等
_______________的菱形是正方形
一个角
是直角
有一个角是直角
要点解读
有一组邻边相等并且有一个角是直角的平行四边形是正方形。
既是矩形又是菱形(或者既是菱形又是矩形)的四边形是正方形。
(1)一组邻边相等的矩形是正方形;
(2)有一个角是直角的菱形是正方形。
要点解读
5种判定方法
邻边相等
有一个角是直角
对角线相等
对角线互相垂直
三个角都是直角
四条边都相等
邻边相等
有一个角是直角
学以致用
例 1
如图,在△ABC中,∠ACB=90°,CD平分∠ACB,DE ⊥BC于E,
DF ⊥AC于F,求证:四边形CFDE是正方形。
A
B
C
D
E
F
【变式】如图,在△ABC中,∠ACB=90°,∠CAB、 ∠ABC的平分线交
于点D,DE ⊥BC于E ,DF ⊥AC于F.求证:四边形CFDE是正方形。
A
B
C
D
F
E
G
学以致用
例 2
如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,AN是△ABC
外角∠CAM的平分线,CE⊥AN,垂足为D,连接DE交AC于点F.
(1)求证:四边形ADCE为矩形;
A
B
C
D
E
F
N
M
(2)当△ABC满足什么条件,四边形ADCE是一个正方形?并出证明;
(3) 在(2)的条件下,若AB=AC=2,求正方形ADCE的周长。
【变式】如图,在△ABC中,AB=AC,AD是△ABC的角平分线,点O为
AB的中点,连结DO并延长到点E,使OE=OD,连结AE,BE.
(1)求证:四边形AEBD为矩形;
(2)当△ABC满足什么条件,四边形AEBD是一个正方形?并出证明。
B
A
C
D
O
E
学以致用
例 3
如图所示,在△ABE中,D是BC边上的一动点(不与B、C重合),
DE//AC交AB于点E,DF//AB交AC于F.
(1)试探索AD满足什么条件时,四边形AEDF是菱形,并给出证明;
(2)在(1)的条件下, △ABC满足什么条件时,四边形AEDF是正方形.
A
B
C
D
E
F
数 学 活 动 室
学 以 致 用
如图,已知在□ABCD中,对角线AC,BD交于点O,E是BD的延长线上的点,且EA=EC.
(1)求证:四边形ABCD是菱形;
(2)若∠DAC=∠EAD+∠AED,求证:四边形ABCD是正方形。
A
B
C
D
E
O
我的收获是……
这节课我学到了什么?
我还有……的疑惑
小 结
