华师大版八年级上册11.1.1 平方根课件(共14张PPT)
文档属性
| 名称 | 华师大版八年级上册11.1.1 平方根课件(共14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-09 12:09:51 | ||
图片预览






文档简介
(共14张PPT)
华东师大版第11章 数的开方
八年级(上)
求几个相同因式的积的运算叫做乘方。
情境激疑
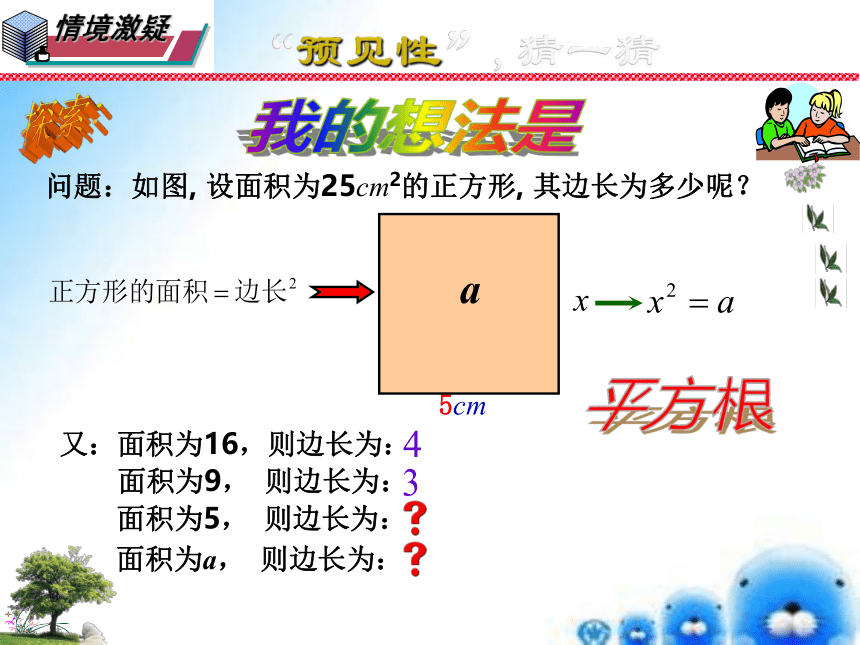
问题:如图, 设面积为25cm2的正方形, 其边长为多少呢?
25cm2
5cm
又:面积为16,则边长为:
16
面积为9, 则边长为:
9
面积为5, 则边长为:
面积为a, 则边长为:
a
x
探究发现
如果一个数x的平方等于a,那么这个数x叫做a的平方根.
就是说:当 时 , 称 x 是 a 的平方根。
(1)叙述:在a是非负数的前提下,a是x的平方,反之,x是a的平方根;
(2)求一个非负数平方根的运算叫做开平方;
(3)开平方与平方的关系是互逆运算。
探究发现
通过刚才的探究活动,大家清楚地感到:
因此,5是25的一个平方根;
因此,4是16的一个平方根;
(1)是否存在其它的数,使它的平方也等于25、16呢?
(2)0的平方根是多少?负数的平方根呢?
(3)通过刚才的研讨,你有何收获?
探究发现
(Ⅰ)一个正数有两个平方根,它们互为相反数;
(Ⅱ)0有一个平方根,它是0本身;
(Ⅲ)负数没有平方根.
探究发现
(Ⅰ)一个正数a的正的平方根,用符号:
正数a的负的平方根,用符号表示为:
这两个平方根合起来可以记作:
读作“二次根号a”。
(Ⅱ)当根指数为2时,可以省略不写;
(Ⅲ)特别规定:0的平方根记为:
学以致用
例 1
求下列各数的平方根:
(1)100 (2)0.49 (3) (4)
你是怎么想的?
【归纳】(1)求平方根时,若被开方数是带分数,应先将带分数化为假分数后
再求平方根。(2)要求一个数的平方根,应先观察哪些数的平方等于这个数。
解:(1)∵
,
∴100的平方根是±10
你会做了吗?试一试吧!
学以致用
例 2
下列各数有平方根吗?如果有,求出它的平方根;如果没有,说
明理由。
(1)-64 (2)0 (3)
解:(1)因为-64是负数,所以-64没有平方根;
(2)0有平方根,这就是0本身;
(3)因为 ,所以 有两个平方根,即
(1)判断一个数是否有平方根,应根据最终结果确定;
(2)注意平方根的符号书写。
学以致用
例 3
计算下列各题:
(1) (2) (3)
(4) (5) (6)
你是怎样考虑的?
学以致用
例 3
解方程:
(1)
解:
记住两种情况哟!
(2)
(3)
解:
解:
或
?
数 学 活 动 室
经 典 数 学
1.求下列各数的平方根:
(1)81 (2) 0.64 (3) (4)
(1) (2)
2.解下列方程:
(3) (4)
我的收获是……
这节课我学到了什么?
我还有……的疑惑
小 结
扩展题
1.已知一个正数的平方根是3m-2和5m+6,求这个数;
2.若2a-1的平方根是±3,3a+b-1的平方根是±4 ,求a+2b的平方根。
华东师大版第11章 数的开方
八年级(上)
求几个相同因式的积的运算叫做乘方。
情境激疑
问题:如图, 设面积为25cm2的正方形, 其边长为多少呢?
25cm2
5cm
又:面积为16,则边长为:
16
面积为9, 则边长为:
9
面积为5, 则边长为:
面积为a, 则边长为:
a
x
探究发现
如果一个数x的平方等于a,那么这个数x叫做a的平方根.
就是说:当 时 , 称 x 是 a 的平方根。
(1)叙述:在a是非负数的前提下,a是x的平方,反之,x是a的平方根;
(2)求一个非负数平方根的运算叫做开平方;
(3)开平方与平方的关系是互逆运算。
探究发现
通过刚才的探究活动,大家清楚地感到:
因此,5是25的一个平方根;
因此,4是16的一个平方根;
(1)是否存在其它的数,使它的平方也等于25、16呢?
(2)0的平方根是多少?负数的平方根呢?
(3)通过刚才的研讨,你有何收获?
探究发现
(Ⅰ)一个正数有两个平方根,它们互为相反数;
(Ⅱ)0有一个平方根,它是0本身;
(Ⅲ)负数没有平方根.
探究发现
(Ⅰ)一个正数a的正的平方根,用符号:
正数a的负的平方根,用符号表示为:
这两个平方根合起来可以记作:
读作“二次根号a”。
(Ⅱ)当根指数为2时,可以省略不写;
(Ⅲ)特别规定:0的平方根记为:
学以致用
例 1
求下列各数的平方根:
(1)100 (2)0.49 (3) (4)
你是怎么想的?
【归纳】(1)求平方根时,若被开方数是带分数,应先将带分数化为假分数后
再求平方根。(2)要求一个数的平方根,应先观察哪些数的平方等于这个数。
解:(1)∵
,
∴100的平方根是±10
你会做了吗?试一试吧!
学以致用
例 2
下列各数有平方根吗?如果有,求出它的平方根;如果没有,说
明理由。
(1)-64 (2)0 (3)
解:(1)因为-64是负数,所以-64没有平方根;
(2)0有平方根,这就是0本身;
(3)因为 ,所以 有两个平方根,即
(1)判断一个数是否有平方根,应根据最终结果确定;
(2)注意平方根的符号书写。
学以致用
例 3
计算下列各题:
(1) (2) (3)
(4) (5) (6)
你是怎样考虑的?
学以致用
例 3
解方程:
(1)
解:
记住两种情况哟!
(2)
(3)
解:
解:
或
?
数 学 活 动 室
经 典 数 学
1.求下列各数的平方根:
(1)81 (2) 0.64 (3) (4)
(1) (2)
2.解下列方程:
(3) (4)
我的收获是……
这节课我学到了什么?
我还有……的疑惑
小 结
扩展题
1.已知一个正数的平方根是3m-2和5m+6,求这个数;
2.若2a-1的平方根是±3,3a+b-1的平方根是±4 ,求a+2b的平方根。
