华师大版数学八年级上册12.5.2平方差公式进行因式分解 课件(共13张PPT)
文档属性
| 名称 | 华师大版数学八年级上册12.5.2平方差公式进行因式分解 课件(共13张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 664.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-09 14:59:07 | ||
图片预览





文档简介
(共13张PPT)
问题:什么叫多项式的因式分解
判断下列变形过程,哪个是因式分解?
(1) (x-2)(x-2)=x2- 4
(2) x2- 4+3x=(x+2)(x-2)+3x
(3) 7m-7n-7=7(m-n-1)
多项式的因式分解其实是整式乘法的逆用,也就是把一个多项式化成了几个整式的积的形式
问题:你学了什么方法进行分解因式?
提公因式法
把下列各式因式分解:
(1) ax - ay
(2) 9a2 - 6ab+3a
(3) 3a(a+b)-5(a+b)
= a( x – y )
=3a(a-2b+1)
=(a+b)(3a - 5)
知识探索
能否用提公因式的方法把多项式
x2-25,9x2-y2分解因式
提示:a2-b2=(a+b)(a-b)
9x2-y2
解:x2-25
= x2 - 52
=(x+5)(x-5)
=(3x)2-y2
=(3x+y)(3x-y)
利用平方差公式进行因式分解
知识探索
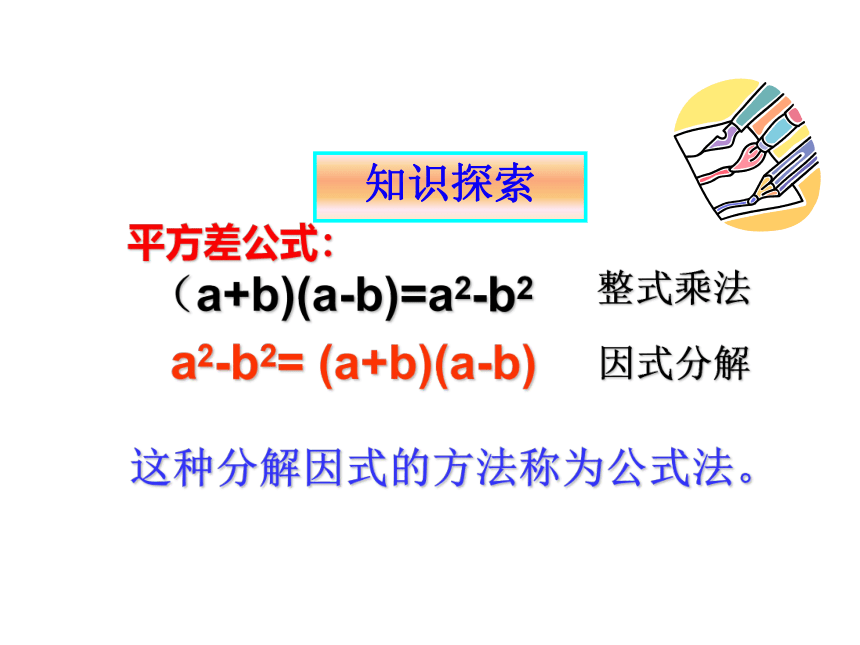
平方差公式:
(a+b)(a-b)=a2-b2
整式乘法
因式分解
这种分解因式的方法称为公式法。
a2-b2= (a+b)(a-b)
符合用平方差公式分解因式的条件
a2-b2 =(a+b)(a-b)
1、必须是二项式
2、两项的符号相反
3、每一项都能写成平方的形式
例题:分解因式
1.4x2-9
2.(x+p)2-(x+q)2
=(2x)2-32
=(2x+3)(2x-3)
=(x+p+x+q)(x+p-x-q)
=(2x+p+q)(p-q)
注:(1)使用平方差公式分解因式时,必须先把原多项式写成两“数”平方差的形式,再分解因式,即用公式分解因式时,必须认准其中的“a”与“b”。
(2)公式中的a、b即可以是单项式,也可以是多项式。
下列多项式能否用平方差公式来分解因式?
(1) x2 + y2
(2) x2 - y2
(3) -x2+y2
(4) -x2 - y2
因式分解:
1、 – a4 + 16
2、 4(a+2)2 - 9(a - 1)2
3、 (x+y+z)2 - (x-y-z)2
1、下列多项式中,能用
平方差分解因式的是( )
A、x2 -xy B、x2 +xy
C、-x2 +y2 D、x2+y2
2、分解因式:
(1)a2 -144b2
(2)16(x+y)2 -25(x-y)2
c
=a2-(12b)2
=(a+12b)(a-12b)
=[4(x+y)]2-[5(x-y)]2
=[4(x+y)+5(x-y)][4(x+y)-5(x-y)]
=(9x-y)(9y-x)
分解因式:
1.a2b- 4b
2.a2(x-y)-x+y
=b(a2-4)
=b(a+2)(a-2)
=(x-y)(a2-1)
=(x-y)(a+1)(a-1)
注:分解因式,必须进行到每一个因式都不能再分解为止 。
1.-4x2y2-6x3y2
2.a2(x-1)+b2(1-x)
3.x3-9x
分解因式
=-2x2y2(2+3x)
=(x-1)(a2-b2)
=(x-1)(a+b)(a-b)
=x(x2-9)
=x(x+3)(x-3)
1.如果多项式各项含有公因式,则第一步是提出这个公因式
2.如果多项式各项没有公因式,则第一步考虑用公式分解因式
3.第一步分解因式以后,所含的多项式还可以继续分解,则需要进一步分解因式.直到每个多项式因式都不能分解为止
问题:什么叫多项式的因式分解
判断下列变形过程,哪个是因式分解?
(1) (x-2)(x-2)=x2- 4
(2) x2- 4+3x=(x+2)(x-2)+3x
(3) 7m-7n-7=7(m-n-1)
多项式的因式分解其实是整式乘法的逆用,也就是把一个多项式化成了几个整式的积的形式
问题:你学了什么方法进行分解因式?
提公因式法
把下列各式因式分解:
(1) ax - ay
(2) 9a2 - 6ab+3a
(3) 3a(a+b)-5(a+b)
= a( x – y )
=3a(a-2b+1)
=(a+b)(3a - 5)
知识探索
能否用提公因式的方法把多项式
x2-25,9x2-y2分解因式
提示:a2-b2=(a+b)(a-b)
9x2-y2
解:x2-25
= x2 - 52
=(x+5)(x-5)
=(3x)2-y2
=(3x+y)(3x-y)
利用平方差公式进行因式分解
知识探索
平方差公式:
(a+b)(a-b)=a2-b2
整式乘法
因式分解
这种分解因式的方法称为公式法。
a2-b2= (a+b)(a-b)
符合用平方差公式分解因式的条件
a2-b2 =(a+b)(a-b)
1、必须是二项式
2、两项的符号相反
3、每一项都能写成平方的形式
例题:分解因式
1.4x2-9
2.(x+p)2-(x+q)2
=(2x)2-32
=(2x+3)(2x-3)
=(x+p+x+q)(x+p-x-q)
=(2x+p+q)(p-q)
注:(1)使用平方差公式分解因式时,必须先把原多项式写成两“数”平方差的形式,再分解因式,即用公式分解因式时,必须认准其中的“a”与“b”。
(2)公式中的a、b即可以是单项式,也可以是多项式。
下列多项式能否用平方差公式来分解因式?
(1) x2 + y2
(2) x2 - y2
(3) -x2+y2
(4) -x2 - y2
因式分解:
1、 – a4 + 16
2、 4(a+2)2 - 9(a - 1)2
3、 (x+y+z)2 - (x-y-z)2
1、下列多项式中,能用
平方差分解因式的是( )
A、x2 -xy B、x2 +xy
C、-x2 +y2 D、x2+y2
2、分解因式:
(1)a2 -144b2
(2)16(x+y)2 -25(x-y)2
c
=a2-(12b)2
=(a+12b)(a-12b)
=[4(x+y)]2-[5(x-y)]2
=[4(x+y)+5(x-y)][4(x+y)-5(x-y)]
=(9x-y)(9y-x)
分解因式:
1.a2b- 4b
2.a2(x-y)-x+y
=b(a2-4)
=b(a+2)(a-2)
=(x-y)(a2-1)
=(x-y)(a+1)(a-1)
注:分解因式,必须进行到每一个因式都不能再分解为止 。
1.-4x2y2-6x3y2
2.a2(x-1)+b2(1-x)
3.x3-9x
分解因式
=-2x2y2(2+3x)
=(x-1)(a2-b2)
=(x-1)(a+b)(a-b)
=x(x2-9)
=x(x+3)(x-3)
1.如果多项式各项含有公因式,则第一步是提出这个公因式
2.如果多项式各项没有公因式,则第一步考虑用公式分解因式
3.第一步分解因式以后,所含的多项式还可以继续分解,则需要进一步分解因式.直到每个多项式因式都不能分解为止
