8.3 动能和动能定理 课件 高一下学期物理人教版(2019)必修第二册(共14张PPT)
文档属性
| 名称 | 8.3 动能和动能定理 课件 高一下学期物理人教版(2019)必修第二册(共14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 944.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-01-09 15:13:25 | ||
图片预览




文档简介
(共14张PPT)
第八章 机械能守恒定律
第3节 动能和动能定理
【回顾】
丙
"
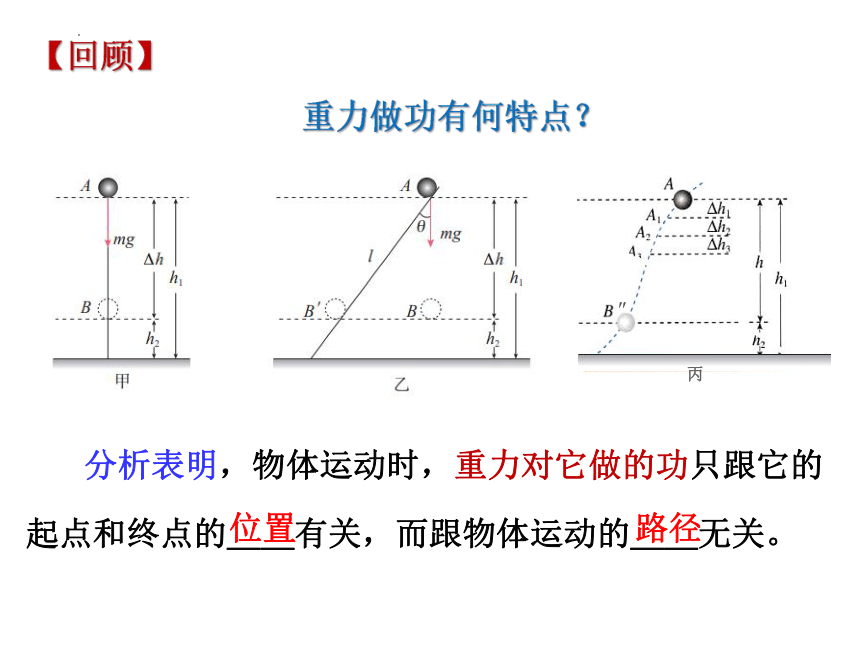
重力做功有何特点?
分析表明,物体运动时,重力对它做的功只跟它的
起点和终点的__有关,而跟物体运动的__无关。
位置
路径
【回顾】
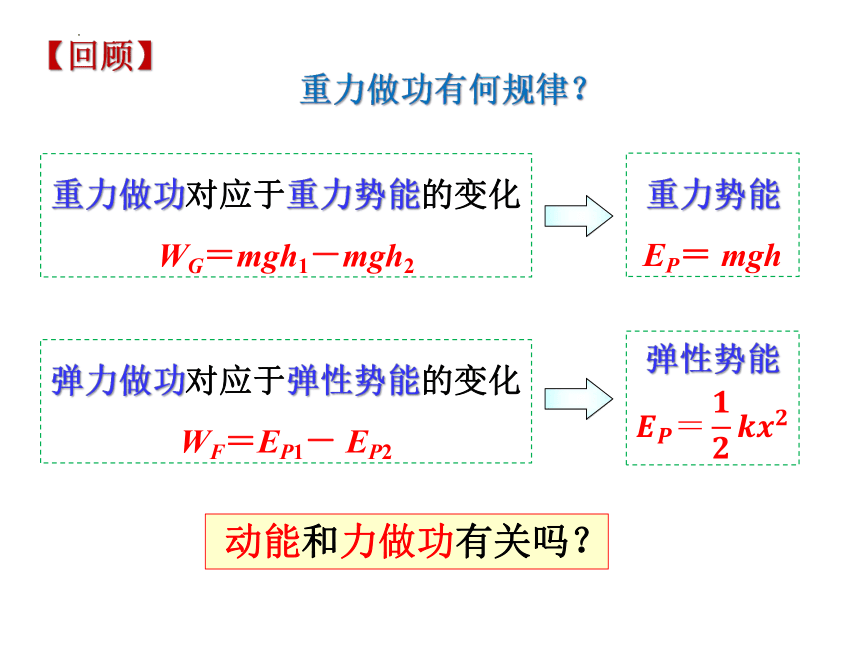
重力做功有何规律?
重力做功对应于重力势能的变化
WG=mgh1-mgh2
重力势能
EP= mgh
弹力做功对应于弹性势能的变化
WF=EP1- EP2
弹性势能
动能和力做功有关吗?
【问题】
物体的动能跟物体的质量和速度都有关系。物体的质量越大,速度越大,它的动能就越大。炮弹在炮筒内推力的作用下速度越来越大,动能增加。这种情况下推力对物体做了功。
你还能举出其他例子,
说明动能和力做的功有关吗?
这对于定量研究动能有什么启发呢?
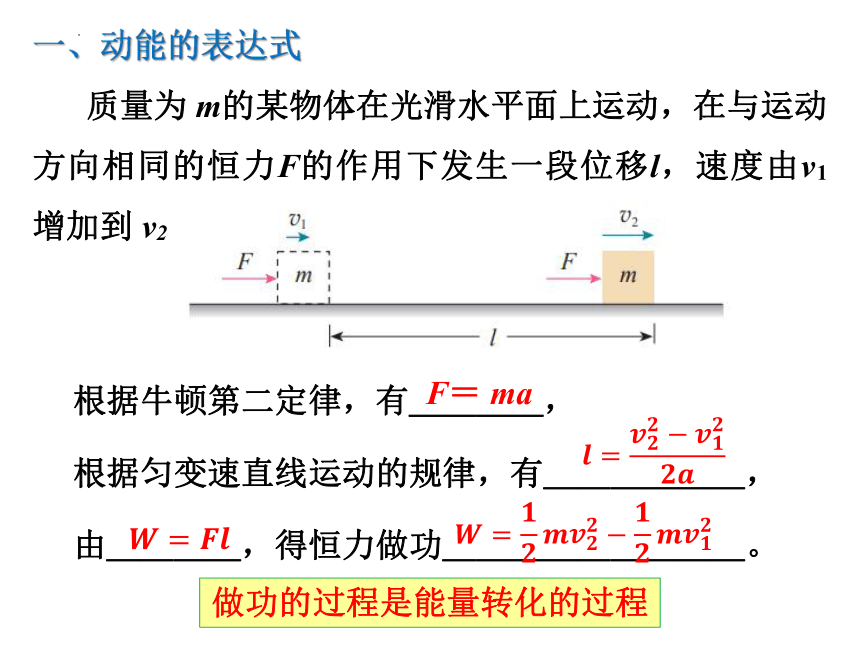
一、动能的表达式
质量为 m的某物体在光滑水平面上运动,在与运动方向相同的恒力F的作用下发生一段位移l,速度由v1增加到 v2
根据牛顿第二定律,有____,
根据匀变速直线运动的规律,有______,
由____,得恒力做功_________。
F= ma
做功的过程是能量转化的过程
二、动能
1.定义:在物理学中,把___叫做物体的动能;
2.公式:_____;
3.单位:___,其中
1kg·(m/s)2=___
=__;
4.特点:
(1)动能是_量,只有正值,没有__;
(2)动能是__量,具有__性。
焦耳J
1N·m
1J
标
方向
状态
相对
三、动能定理
1.表述:力在一个过程中对物体做的功,等于物体在这个过程中_____;
2.公式:______;
【说明】W是作用在物体
上一切外力做功的__,
Ek1是物体___的动能, Ek2是物体___的动能。
3.关系:
(1)合力做正功,动能__,即________;
(2)合力做负功,动能__,即________。
动能的变化
W=Ek2- Ek1
总和
初状态
末状态
增大
W>0,Ek2>Ek1
减小
W<0,Ek2<Ek1
【例题1】一架喷气式飞机,质量m为7.0×104kg,起飞过程中从静止开始滑跑。当位移l达到2.5×103m 时,速度达到起飞速度80m/s。在此过程中,飞机受到的平均阻力是飞机所受重力的1/50。g取10m/s2 ,求飞机平均牵引力的大小。
解:
合力对飞机做功
W=(F牵-F阻)l =(F牵-kmg)l
飞机的初动能
Ek1=0
飞机的末动能
根据动能定理W=Ek2- Ek1,有
代入已知数据,得飞机的平均牵引力大小为
F牵=1.04×10 5N
解:
根据匀变速直线运动的速度与位移关系,有
v 2=2al
根据牛顿第二定律,有
F牵-kmg=ma
代入数据,得飞机的平均牵引力大小为
F牵=1.04×10 5N
【对比】
(根据牛顿运动定律与运动学规律求解)
【例题2】人们有时用“打夯”的方式把松散的地面夯实(如图所示)。设某次打夯符合以下模型:两人同时通过绳子对重物各施加一个力,力的大小均为320N,方向都与竖直方向成37°,
重物离开地面30cm后人停止
施力,最后重物自由下落把
地面砸深2cm。已知重物的
质量为50kg,g取10m/s2, cos37°=0.8。求:
(1)重物刚落地时的速度是多大?
(2)重物对地面的平均冲击力是多大?
解:
(1)两根绳子对重物的合力
F合= 2F cos 37°=2×320×0.8 N=512 N
由甲至丙只有绳子的拉力做功,应用动能定理得
则重物刚落地时的速度是 v=2 .5m/s
解:
(2)由丙至丁的过程中,应用动能定理得
重物受到的平均阻力大小是 F阻=8 .3×103N
重物对地面的平均冲击力大小是 8 .3×103N
【小结】
一、动能
二、动能定理 W=Ek2- Ek1
科学方法:演绎推理是从一般性结论推出个别性结论的方法,即从已知的某些一般性原理、定理、法则、公理或科学概念出发,推出新结论的一种思维活动。
提示:动能定理广泛适用于恒力或变力做功、直线或曲线运动、单个或多个物体、全段或分段过程。
第八章 机械能守恒定律
第3节 动能和动能定理
【回顾】
丙
"
重力做功有何特点?
分析表明,物体运动时,重力对它做的功只跟它的
起点和终点的__有关,而跟物体运动的__无关。
位置
路径
【回顾】
重力做功有何规律?
重力做功对应于重力势能的变化
WG=mgh1-mgh2
重力势能
EP= mgh
弹力做功对应于弹性势能的变化
WF=EP1- EP2
弹性势能
动能和力做功有关吗?
【问题】
物体的动能跟物体的质量和速度都有关系。物体的质量越大,速度越大,它的动能就越大。炮弹在炮筒内推力的作用下速度越来越大,动能增加。这种情况下推力对物体做了功。
你还能举出其他例子,
说明动能和力做的功有关吗?
这对于定量研究动能有什么启发呢?
一、动能的表达式
质量为 m的某物体在光滑水平面上运动,在与运动方向相同的恒力F的作用下发生一段位移l,速度由v1增加到 v2
根据牛顿第二定律,有____,
根据匀变速直线运动的规律,有______,
由____,得恒力做功_________。
F= ma
做功的过程是能量转化的过程
二、动能
1.定义:在物理学中,把___叫做物体的动能;
2.公式:_____;
3.单位:___,其中
1kg·(m/s)2=___
=__;
4.特点:
(1)动能是_量,只有正值,没有__;
(2)动能是__量,具有__性。
焦耳J
1N·m
1J
标
方向
状态
相对
三、动能定理
1.表述:力在一个过程中对物体做的功,等于物体在这个过程中_____;
2.公式:______;
【说明】W是作用在物体
上一切外力做功的__,
Ek1是物体___的动能, Ek2是物体___的动能。
3.关系:
(1)合力做正功,动能__,即________;
(2)合力做负功,动能__,即________。
动能的变化
W=Ek2- Ek1
总和
初状态
末状态
增大
W>0,Ek2>Ek1
减小
W<0,Ek2<Ek1
【例题1】一架喷气式飞机,质量m为7.0×104kg,起飞过程中从静止开始滑跑。当位移l达到2.5×103m 时,速度达到起飞速度80m/s。在此过程中,飞机受到的平均阻力是飞机所受重力的1/50。g取10m/s2 ,求飞机平均牵引力的大小。
解:
合力对飞机做功
W=(F牵-F阻)l =(F牵-kmg)l
飞机的初动能
Ek1=0
飞机的末动能
根据动能定理W=Ek2- Ek1,有
代入已知数据,得飞机的平均牵引力大小为
F牵=1.04×10 5N
解:
根据匀变速直线运动的速度与位移关系,有
v 2=2al
根据牛顿第二定律,有
F牵-kmg=ma
代入数据,得飞机的平均牵引力大小为
F牵=1.04×10 5N
【对比】
(根据牛顿运动定律与运动学规律求解)
【例题2】人们有时用“打夯”的方式把松散的地面夯实(如图所示)。设某次打夯符合以下模型:两人同时通过绳子对重物各施加一个力,力的大小均为320N,方向都与竖直方向成37°,
重物离开地面30cm后人停止
施力,最后重物自由下落把
地面砸深2cm。已知重物的
质量为50kg,g取10m/s2, cos37°=0.8。求:
(1)重物刚落地时的速度是多大?
(2)重物对地面的平均冲击力是多大?
解:
(1)两根绳子对重物的合力
F合= 2F cos 37°=2×320×0.8 N=512 N
由甲至丙只有绳子的拉力做功,应用动能定理得
则重物刚落地时的速度是 v=2 .5m/s
解:
(2)由丙至丁的过程中,应用动能定理得
重物受到的平均阻力大小是 F阻=8 .3×103N
重物对地面的平均冲击力大小是 8 .3×103N
【小结】
一、动能
二、动能定理 W=Ek2- Ek1
科学方法:演绎推理是从一般性结论推出个别性结论的方法,即从已知的某些一般性原理、定理、法则、公理或科学概念出发,推出新结论的一种思维活动。
提示:动能定理广泛适用于恒力或变力做功、直线或曲线运动、单个或多个物体、全段或分段过程。
