第八章 平行线的有关证明单元测试题(含答案)
文档属性
| 名称 | 第八章 平行线的有关证明单元测试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 6.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-09 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第八章综合测试题
时间:60分钟 满分:100分 得分:____________
一、选择题(每题3分,共30分)
1.如图,直线a,b被直线c所截,且a∥b,若∠1等于60°,则∠2的度数是( )
A.70° B.60° C.50° D.40°
2.下列命题中是真命题的是 ( )
A.平行于同一条直线的两条直线互相平行 B.两直线平行,同旁内角相等
C.两个角相等,这两个角一定是对顶角 D.相等的两个角是平行线所得的内错角
3.一个三角形三个内角的度数之比为1:2:3,则这个三角形一定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰直角三角形
4.如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )
A.315° B.270° C.180° D.135°
5.将一张矩形纸片折叠成如图所示的图形,若∠CAB=30°,则∠ACB的度数是 ( )
A.45° B.55° C.65° D.75°
6.如图,直线a,b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判定a∥b的是 ( )
A.①② B.③④ C.①③④ D.①②③④
7.一块直角三角板按如图所示方式放置在一张长方形纸条上,若∠1=28°,则∠2的度数为 ( )
A.28° B.56° C.36° D.62°
8.如图,AB∥CD,则下列式子一定成立的是( )
A.∠1=∠3 B.∠2=∠3 C.∠1=∠2+∠3 D.∠3=∠1+∠2
9.如图,将一张三角形纸片ABC的一角折叠,使点A落在△ABC外的A′处,折痕为DE,若∠A=α,∠BDA′=β,∠CEA′=γ,那么下列式子中正确的是( )
A.β=2α+γ B. β=α+γ C. β=α+2γ D.β=180-α-γ
10.如图,若∠1=∠2,DE∥BC,则①FG∥DC;②∠AED=∠ACB;③CD平分∠ACB;④∠1+∠B=90°;⑤∠BFG=∠BDC.其中正确的结论是( )
A.①②③ B.①②⑤ C.①③④ D.③④
二、填空题(每题3分,共18分)
11.能说明命题“对于任何实数a,如果,那么.”是假命题的一个反例可以是_____________________________________.
12.如图,∵∠1=∠2,∴________∥__________.
∵∠2=__________,∴_________∥__________(同位角相等,两直线平行).
∴AC∥FG(_________________________________________)
13.甲、乙、丙、丁与小强这5位同学一起参加象棋比赛,每两人都要赛一盘,到目前为止,甲赛了4盘,乙赛了3盘,丙赛了2盘,丁赛了1盘.则小强已经赛了 盘.
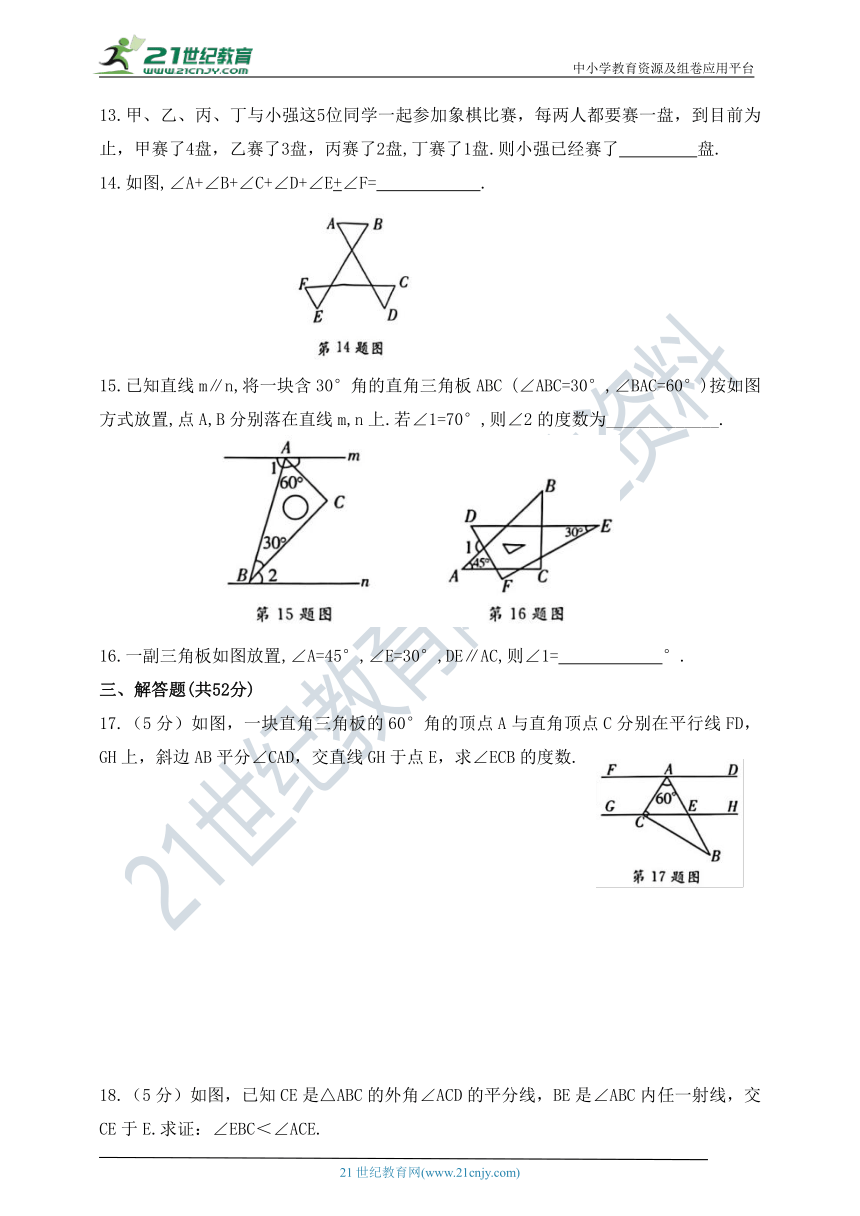
14.如图,∠A+∠B+∠C+∠D+∠E+∠F= .
15.已知直线m∥n,将一块含30°角的直角三角板ABC (∠ABC=30°,∠BAC=60°)按如图方式放置,点A,B分别落在直线m,n上.若∠1=70°,则∠2的度数为_____________.
16.一副三角板如图放置,∠A=45°,∠E=30°,DE∥AC,则∠1= °.
三、解答题(共52分)
17.(5分)如图,一块直角三角板的60°角的顶点A与直角顶点C分别在平行线FD,GH上,斜边AB平分∠CAD,交直线GH于点E,求∠ECB的度数.
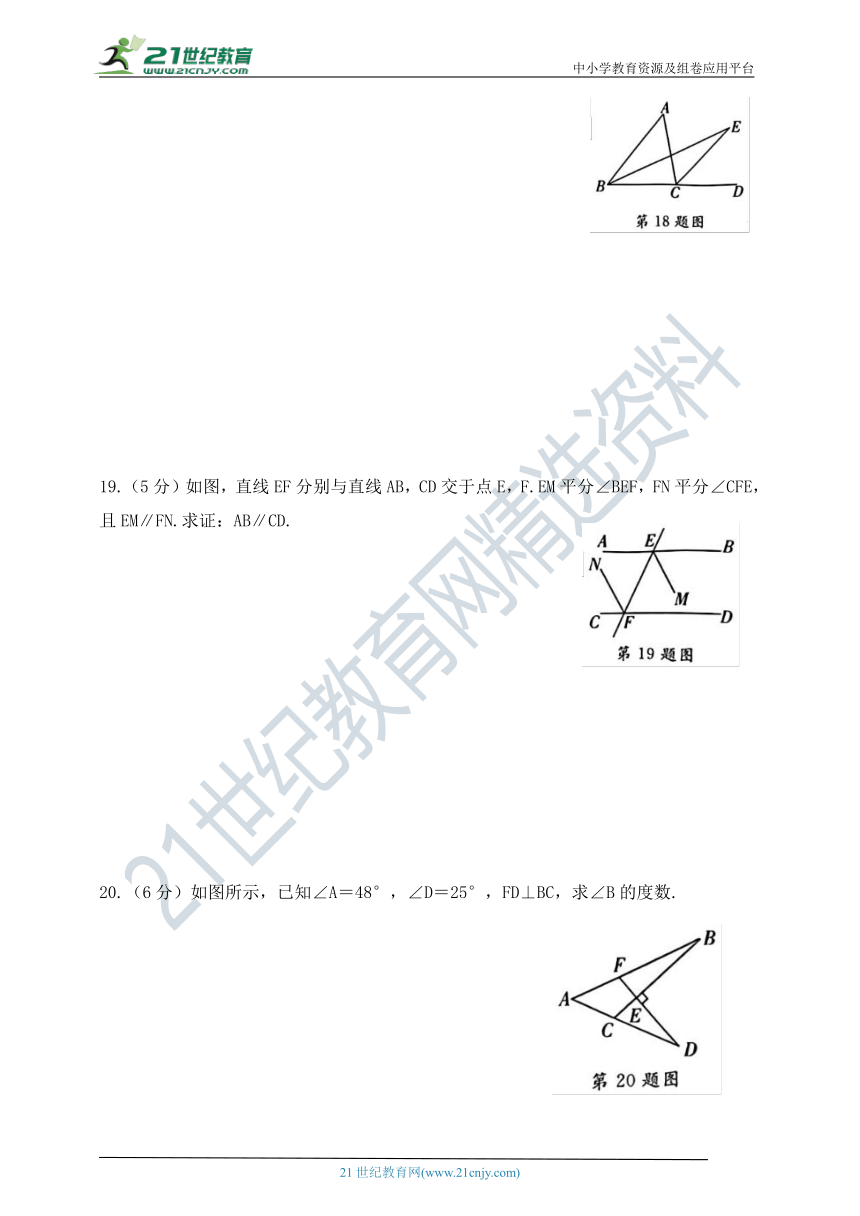
18.(5分)如图,已知CE是△ABC的外角∠ACD的平分线,BE是∠ABC内任一射线,交CE于E.求证:∠EBC<∠ACE.
19.(5分)如图,直线EF分别与直线AB,CD交于点E,F.EM平分∠BEF,FN平分∠CFE,且EM∥FN.求证:AB∥CD.
20.(6分)如图所示,已知∠A=48°,∠D=25°,FD⊥BC,求∠B的度数.
21.(6分)AB∥CD,连接CA延长至点H,CF平分∠ACD,CE⊥CF,∠GAH与∠AFC互余.
(1)试判断AG与CE的位置关系,并说明理由;
(2)若∠GAF=110°,求∠AFC的度数.
22.(6分)如图,在四边形ABCD中,∠D+∠ABC=180°,BE平分∠ABC交CD于点E,连接AE,BE.
(1)若∠C=∠1,求证:∠CBE=∠AED;
(2)若∠C=80°,∠D=124°,求∠CEB的度数.
23.(9分)已知:如图,AB∥CD.
(1)如图1,猜想并写出∠B,∠D,∠E之间的数量关系.以下图2,图3,图4是三种不同角度思考采用的不同添加辅助线的方式,请你选择其中的两种方式说明理由;
(2)在图4中,如果BE,DE分别平分∠ABD,∠CDB,则∠E的度数是多少 (直接写出答案)
(3)根据以上推理,直接写出图5,图6,图7中的∠B,∠D,∠E之间的数量关系.
24.(10分)如图,在△ABC中,∠ABC=40°,∠ACB=90°,AE平分∠BAC交BC于点E.P是边BC上的动点(不与B,C重合),连结AP,将△APC沿AP翻折得△APD,连接DC,记∠BCD=α.
(1)如图,当P与E重合时,求α的度数;
(2)当P与E不重合时,记∠BAD=β,探究α与β的数量关系.
参考答案
1.B 2.A 3.B 4.B 5.D 6.D 7.D 8.D
9.A 解析:由折叠,得∠A=∠A′,
∵∠BDA′=∠A+∠AFD,∠AFD=∠A′+∠CEA′,
∵∠A′=∠A=α,∠BDA′=β,∠CEA′=γ,
∴∠BDA′=β=∠A+∠A′+∠CEA′=α+α+γ=2α+γ.
故选:A.
10.B
11.(示例)如果3 =( -3) , 那么3≠-3
12.AC DE ∠4 DE FG 平行于同一条直线的两条直线互相平行
13.2 解析:由于甲已经赛了4盘,则甲与乙、丙、丁、小强各赛了一盘;
因为丁赛了1盘,则丁这一盘是与甲赛的,没有与其他人赛;
因为乙赛了3盘,则乙与甲、丙、小强各下了一盘;
因为丙赛了2盘,则丙是与甲和乙赛的.
所以小强赛了两盘,是与甲和乙赛的.
故答案为:2.
14.360° 15.40° 16.105
17.解:∵AB平分∠CAD,∠CAE=60°,
∴∠CAD=2×60°=120°.
又∵FD∥GH,
∴∠ACH=180°-120°=60°,
∴∠ECB=∠ACB-∠ACH=90°-60°=30°.
18.证明: ∵CE是△ABC的外角∠ACD的平分线,∴∠ACE=∠ECD.
∴∠ECD>∠EBC,∴∠ACE>∠EBC.
即∠EBC<∠ACE.
19.证明:∵EM平分∠BEF,FN平分∠CFE,
∵EM∥FN,∴∠MEF=∠NFE.
即∠BEF=∠CFE.∴AB∥CD.
20.解:∵∠A=48°,∠D=25°,∴∠BFE=∠A+∠D=73°,
又∵FD⊥BC于E,∴∠BEF=90°;
∴Rt△BFE中,∠B=180°-∠BEF-∠BFE=17°,即∠B=17°.
21.解:(1)AG∥CE.
证明:∵AB∥CD,∴∠AFC=∠DCF,
∵CF平分∠ACD,∴∠FCD=∠ACF.∴∠AFC=∠ACF,
又∵CE⊥CF,∠GAH与∠AFC互余.∴∠ECH+∠ACF=90°,∠GAH+∠AFC=90°,
∴∠ECH=∠GAH,∴AG∥CE;
(2)∵AB∥CD,∴∠HAF=∠HCD.
由(1)知,∠ECH=∠GAH,∴∠ECH+∠HCD=∠GAH+∠HAF,∴∠ECD=∠GAF=110°,
又∵CE⊥CF,∴∠ECF=90°,∴∠DCF=∠ECD-∠ECF=20°,∴∠AFC=∠DCF=20°.
22.解:(1)证明:∵∠C+∠CBE+∠CEB=180°,∠AED+∠1+∠CEB=180°,∠C=∠1,
∴∠CBE=∠AED;
(2)∵∠D+∠ABC=180°,∠D=124°,∴∠ABC=56°,
∵BE平分∠ABC,
∵∠C+∠CBE+∠CEB=180°,∠C=80°,∴∠CEB=72°.
∵AB∥CD,EF∥AB,∴EF∥CD.∴∠D=∠DEF.
∵∠BED=∠BEF+∠DEF,∴∠BED=∠B+∠D. ∠B+∠BGE+∠BEG=180°,
∴∠BED=∠B+∠BGE.
∴∠BED=∠B+∠D.
∴∠ABD+∠BDC=∠CDE+∠EDB+∠ABE=180°.
又∵∠DBE+∠BDE+∠BED=180°,
∴∠BED=∠ABE+∠CDE.
(2)∠BED=90°,理由:如图4.
∵AB∥CD,∴∠ABD+∠CDB=180°,
∵BE,DE分别平分∠ABD,∠CDB.
∴∠B+∠1=180°,∠D+∠2=180°,
∴∠B+∠1+∠D+∠2=360°,
即∠B+∠D+∠BED=360°;
∴∠D-∠B=∠BEF-∠DEF=∠BED,
∴∠B+∠BED=∠D;
24.解:(1)∵∠B=40°,∠ACB=90°,∴∠BAC=50°,
∵P与E重合,AE平分∠BAC,∴D在AB边上,AE⊥CD.
∴α=∠ACB-∠ACD=90°-65°=25°;
∴90°-a+β=40°+α,∴2a- β=50° ;
∴90°-α=40°+α+β,
∴2α+β=50°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第八章综合测试题
时间:60分钟 满分:100分 得分:____________
一、选择题(每题3分,共30分)
1.如图,直线a,b被直线c所截,且a∥b,若∠1等于60°,则∠2的度数是( )
A.70° B.60° C.50° D.40°
2.下列命题中是真命题的是 ( )
A.平行于同一条直线的两条直线互相平行 B.两直线平行,同旁内角相等
C.两个角相等,这两个角一定是对顶角 D.相等的两个角是平行线所得的内错角
3.一个三角形三个内角的度数之比为1:2:3,则这个三角形一定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰直角三角形
4.如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )
A.315° B.270° C.180° D.135°
5.将一张矩形纸片折叠成如图所示的图形,若∠CAB=30°,则∠ACB的度数是 ( )
A.45° B.55° C.65° D.75°
6.如图,直线a,b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判定a∥b的是 ( )
A.①② B.③④ C.①③④ D.①②③④
7.一块直角三角板按如图所示方式放置在一张长方形纸条上,若∠1=28°,则∠2的度数为 ( )
A.28° B.56° C.36° D.62°
8.如图,AB∥CD,则下列式子一定成立的是( )
A.∠1=∠3 B.∠2=∠3 C.∠1=∠2+∠3 D.∠3=∠1+∠2
9.如图,将一张三角形纸片ABC的一角折叠,使点A落在△ABC外的A′处,折痕为DE,若∠A=α,∠BDA′=β,∠CEA′=γ,那么下列式子中正确的是( )
A.β=2α+γ B. β=α+γ C. β=α+2γ D.β=180-α-γ
10.如图,若∠1=∠2,DE∥BC,则①FG∥DC;②∠AED=∠ACB;③CD平分∠ACB;④∠1+∠B=90°;⑤∠BFG=∠BDC.其中正确的结论是( )
A.①②③ B.①②⑤ C.①③④ D.③④
二、填空题(每题3分,共18分)
11.能说明命题“对于任何实数a,如果,那么.”是假命题的一个反例可以是_____________________________________.
12.如图,∵∠1=∠2,∴________∥__________.
∵∠2=__________,∴_________∥__________(同位角相等,两直线平行).
∴AC∥FG(_________________________________________)
13.甲、乙、丙、丁与小强这5位同学一起参加象棋比赛,每两人都要赛一盘,到目前为止,甲赛了4盘,乙赛了3盘,丙赛了2盘,丁赛了1盘.则小强已经赛了 盘.
14.如图,∠A+∠B+∠C+∠D+∠E+∠F= .
15.已知直线m∥n,将一块含30°角的直角三角板ABC (∠ABC=30°,∠BAC=60°)按如图方式放置,点A,B分别落在直线m,n上.若∠1=70°,则∠2的度数为_____________.
16.一副三角板如图放置,∠A=45°,∠E=30°,DE∥AC,则∠1= °.
三、解答题(共52分)
17.(5分)如图,一块直角三角板的60°角的顶点A与直角顶点C分别在平行线FD,GH上,斜边AB平分∠CAD,交直线GH于点E,求∠ECB的度数.
18.(5分)如图,已知CE是△ABC的外角∠ACD的平分线,BE是∠ABC内任一射线,交CE于E.求证:∠EBC<∠ACE.
19.(5分)如图,直线EF分别与直线AB,CD交于点E,F.EM平分∠BEF,FN平分∠CFE,且EM∥FN.求证:AB∥CD.
20.(6分)如图所示,已知∠A=48°,∠D=25°,FD⊥BC,求∠B的度数.
21.(6分)AB∥CD,连接CA延长至点H,CF平分∠ACD,CE⊥CF,∠GAH与∠AFC互余.
(1)试判断AG与CE的位置关系,并说明理由;
(2)若∠GAF=110°,求∠AFC的度数.
22.(6分)如图,在四边形ABCD中,∠D+∠ABC=180°,BE平分∠ABC交CD于点E,连接AE,BE.
(1)若∠C=∠1,求证:∠CBE=∠AED;
(2)若∠C=80°,∠D=124°,求∠CEB的度数.
23.(9分)已知:如图,AB∥CD.
(1)如图1,猜想并写出∠B,∠D,∠E之间的数量关系.以下图2,图3,图4是三种不同角度思考采用的不同添加辅助线的方式,请你选择其中的两种方式说明理由;
(2)在图4中,如果BE,DE分别平分∠ABD,∠CDB,则∠E的度数是多少 (直接写出答案)
(3)根据以上推理,直接写出图5,图6,图7中的∠B,∠D,∠E之间的数量关系.
24.(10分)如图,在△ABC中,∠ABC=40°,∠ACB=90°,AE平分∠BAC交BC于点E.P是边BC上的动点(不与B,C重合),连结AP,将△APC沿AP翻折得△APD,连接DC,记∠BCD=α.
(1)如图,当P与E重合时,求α的度数;
(2)当P与E不重合时,记∠BAD=β,探究α与β的数量关系.
参考答案
1.B 2.A 3.B 4.B 5.D 6.D 7.D 8.D
9.A 解析:由折叠,得∠A=∠A′,
∵∠BDA′=∠A+∠AFD,∠AFD=∠A′+∠CEA′,
∵∠A′=∠A=α,∠BDA′=β,∠CEA′=γ,
∴∠BDA′=β=∠A+∠A′+∠CEA′=α+α+γ=2α+γ.
故选:A.
10.B
11.(示例)如果3 =( -3) , 那么3≠-3
12.AC DE ∠4 DE FG 平行于同一条直线的两条直线互相平行
13.2 解析:由于甲已经赛了4盘,则甲与乙、丙、丁、小强各赛了一盘;
因为丁赛了1盘,则丁这一盘是与甲赛的,没有与其他人赛;
因为乙赛了3盘,则乙与甲、丙、小强各下了一盘;
因为丙赛了2盘,则丙是与甲和乙赛的.
所以小强赛了两盘,是与甲和乙赛的.
故答案为:2.
14.360° 15.40° 16.105
17.解:∵AB平分∠CAD,∠CAE=60°,
∴∠CAD=2×60°=120°.
又∵FD∥GH,
∴∠ACH=180°-120°=60°,
∴∠ECB=∠ACB-∠ACH=90°-60°=30°.
18.证明: ∵CE是△ABC的外角∠ACD的平分线,∴∠ACE=∠ECD.
∴∠ECD>∠EBC,∴∠ACE>∠EBC.
即∠EBC<∠ACE.
19.证明:∵EM平分∠BEF,FN平分∠CFE,
∵EM∥FN,∴∠MEF=∠NFE.
即∠BEF=∠CFE.∴AB∥CD.
20.解:∵∠A=48°,∠D=25°,∴∠BFE=∠A+∠D=73°,
又∵FD⊥BC于E,∴∠BEF=90°;
∴Rt△BFE中,∠B=180°-∠BEF-∠BFE=17°,即∠B=17°.
21.解:(1)AG∥CE.
证明:∵AB∥CD,∴∠AFC=∠DCF,
∵CF平分∠ACD,∴∠FCD=∠ACF.∴∠AFC=∠ACF,
又∵CE⊥CF,∠GAH与∠AFC互余.∴∠ECH+∠ACF=90°,∠GAH+∠AFC=90°,
∴∠ECH=∠GAH,∴AG∥CE;
(2)∵AB∥CD,∴∠HAF=∠HCD.
由(1)知,∠ECH=∠GAH,∴∠ECH+∠HCD=∠GAH+∠HAF,∴∠ECD=∠GAF=110°,
又∵CE⊥CF,∴∠ECF=90°,∴∠DCF=∠ECD-∠ECF=20°,∴∠AFC=∠DCF=20°.
22.解:(1)证明:∵∠C+∠CBE+∠CEB=180°,∠AED+∠1+∠CEB=180°,∠C=∠1,
∴∠CBE=∠AED;
(2)∵∠D+∠ABC=180°,∠D=124°,∴∠ABC=56°,
∵BE平分∠ABC,
∵∠C+∠CBE+∠CEB=180°,∠C=80°,∴∠CEB=72°.
∵AB∥CD,EF∥AB,∴EF∥CD.∴∠D=∠DEF.
∵∠BED=∠BEF+∠DEF,∴∠BED=∠B+∠D. ∠B+∠BGE+∠BEG=180°,
∴∠BED=∠B+∠BGE.
∴∠BED=∠B+∠D.
∴∠ABD+∠BDC=∠CDE+∠EDB+∠ABE=180°.
又∵∠DBE+∠BDE+∠BED=180°,
∴∠BED=∠ABE+∠CDE.
(2)∠BED=90°,理由:如图4.
∵AB∥CD,∴∠ABD+∠CDB=180°,
∵BE,DE分别平分∠ABD,∠CDB.
∴∠B+∠1=180°,∠D+∠2=180°,
∴∠B+∠1+∠D+∠2=360°,
即∠B+∠D+∠BED=360°;
∴∠D-∠B=∠BEF-∠DEF=∠BED,
∴∠B+∠BED=∠D;
24.解:(1)∵∠B=40°,∠ACB=90°,∴∠BAC=50°,
∵P与E重合,AE平分∠BAC,∴D在AB边上,AE⊥CD.
∴α=∠ACB-∠ACD=90°-65°=25°;
∴90°-a+β=40°+α,∴2a- β=50° ;
∴90°-α=40°+α+β,
∴2α+β=50°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
