2.4一元一次不等式 课件

课件34张PPT。第四节 一元一次不等式知识点一：一元一次不等式的概念一元一次方程:
方程的两边都是整式，只含有一个未知数；并且未知数的指数是一次，这样的方程叫做一元一次方程.1、方程的两边都是整式2、只有一个未知数3、未知数的指数是一次特点： （1）x=4 （2）3y=30⑷　1.5a+12=0.5a+1请你找出这些不等式有哪些共同的特征？列： （1）x>4 （2）3y>30⑷　1.5a+12≤0.5a+1请你找出这些不等式有哪些共同的特征？ （1）x>4 （2）3y>30⑷　1.5a+12≤0.5a+1请你从下列式子中找出与上面不等式有共同的特征的不等式。 （2）X > 2
(3)x＜ 2x+1(1)a2+1＞ 0(4)y=2y-5（5）ｘ+ｙ>-3一元一次不等式定义：
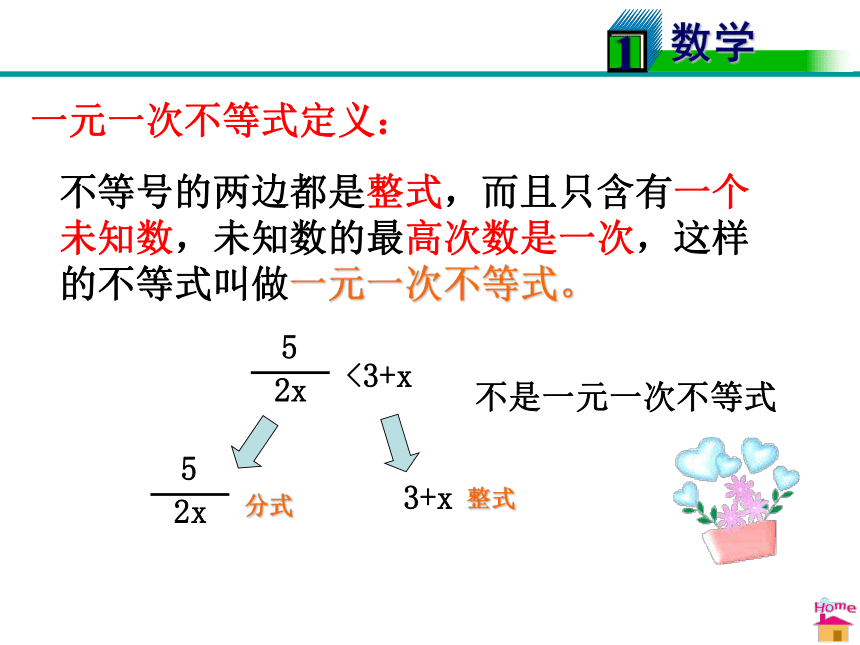
不等号的两边都是整式，而且只含有一个未知数，未知数的最高次数是一次，这样的不等式叫做一元一次不等式。3+x分式整式不是一元一次不等式一元一次不等式定义：
不等号的两边都是整式，而且只含有一个未知数，未知数的最高次数是一次，这样的不等式叫做一元一次不等式。特点： （1）不等号的两边都是整式
（2）只含有一个未知数
（3）未知数的最高次数是1次知识点二：一元一次不等式的解法我们把能使不等式成立的未知数的值的全体叫做不等式的解集，简称不等式的解。把x=5代入不等式3x<18，不等式成立吗？那能否说能使不等式成立的值就是x=5?这样的值有很多请同学们把他们在数轴上指出来X<6不等式3x<18的解是想一想1X=6,x=7呢？想一想2求下列各不等式的解集(1) X+5<3
(2) -3x>30比较(1) X+5=3(2) -3x=30解：两边同时减去5得
X+5-5=3-5
X=-2解：两边同时除以-3得
（-3x）÷（-3）=30÷（-3）
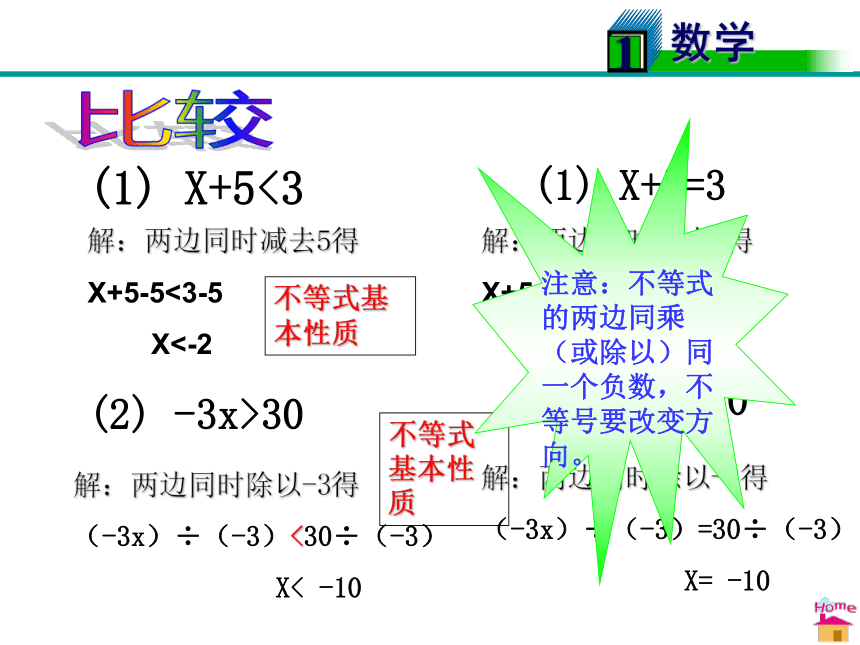
X= -10(1) X+5<3解：两边同时减去5得
X+5-5<3-5
X<-2(2) -3x>30解：两边同时除以-3得
（-3x）÷（-3）<30÷（-3）
X< -10不等式基本性质不等式基本性质比较(1) X+5<3解：两边同时减去5得
X+5-5<3-5
X<-2(2) -3x>30解：两边同时除以-3得
（-3x）÷（-3）<30÷（-3）
X< -10不等式基本性质不等式基本性质解不等式就是利用不等式的基本性质，不等式变形成：
x>a(或x≥a) x 2x+4解不等式7x-2≤9x+3,把解表示在数轴上.不等式的负整数解是x=-1和x=-2. 解: 先在不等式的两边同加上-9x,得
7x-9x-2≤3
再在不等式的两边同加上2,得
7x-9x≤3+2.
合并同类项,得 -2x≤5
两边同除以-2,得 x≥例2并求出不等式的负整数解.7x-2≤9x+3 7x-9x≤3+2把不等式中的任何一项的符号改变后，
从不等号的一边移到另一边，所得到的
不等式仍成立。也就是说，在解不等式
时，移项法则同样适用.-2x≤5移项得两边同除以-2,得 x≥合并同类项下列式子哪些是一元一次不等式？哪些不是一元一次不等式？1、X>0
3、X >2
4、ｘ+ｙ>-3
5、x=-1
√√我选择 我喜欢解下列一元一次不等式.（1）-2x<4
（2）x+1>2x-3解：两边同除以-2，得 x<-2;
解：移项得，4>x ,即 x>4;我选择 我喜欢m取何值时，关于x的方程的解大于1。课外延伸知识点三：一元一次不等式的实际应用1、如图，在△ABC中，AD是BC边上的高，BC=12cm。问高AD的长h等于多少时△ABC的面积是60cm2？ h在怎样的范围时,△ABC的面积才不小于60cm2？h12请试着用不等式来解一解12h÷2=60 h=1012h÷2≥60 h≥102、宾馆里有一座电梯的最大载量为1000千克。两名宾馆服务员要用电梯把一批重物从底层搬到顶层，这两名服务员的身体质量分别为60千克和80千克，货物每箱的质量为50千克，问他们每次最多只能搬运重物多少箱？2、宾馆里有一座电梯的最大载量为1000千克。两名宾馆服务员要用电梯把一批重物从底层搬到顶层，这两名服务员的身体质量分别为60千克和80千克，货物每箱的质量为50千克，问他们每次最多只能搬运重物多少箱？请讨论以下问题：
（1）选择哪一种数学模型？是列方程，还是列不等式？
（2）问题中有哪些相等的数量关系和不等的数量关系？解：设他们每次能搬运重物X箱，根据题意得：
60+80+50X≤1000
解得 X≤17.2
答：他们每次最多能搬运重物17箱。实际问题 数学符号 解决问题 １、抓住关键语句2.用代数式表示各过程量解方程或不等式1.由题意恰当地设未知数建立模型 列方程或不等式２、分析数量关系共同归纳： 例1、有一家庭工厂投资2万元购进一台机器，生产某种商品。这种商品每个的成本是3元，出售价是5元，应付的税款和其他费用是销售收入的10％。问至少需要生产、销售多少个这种商品，才能使所获利润（毛利润减去税款和其他费用)超过投资购买机器的费用?（1）先从所求的量出发考虑问题，至少需要生产、销售多少个商品，使所获利润>购买机器款？（2）每生产、销售一个这样商品的利润是多少元？（3）生产、销售x个这样的商品的利润是多少元？这样我们只要设生产、销售这种商品x个就可以了。5×10%2-5× 10%532解：设生产、销售这种商品X个，则所得利润为（5-3-5×10%）X元。
由题意得；
（5-3-5×10%）X＞20000
解得：X＞13333.3……
答：至少要生产、销售这种商品13334个。 若这家工厂向银行贷款10万元，购进一台机器生产某种零件。已知零件的生产成本为每只7元，销售价为每只10元，应缴纳税款是销售总额的10%，银行年利率为10%，要求经过一年一次性还清贷款。这个家庭工厂这一年至少要生产、销售多少只零件？变式训练（10-7-10×10%）x≥100000×（1+10%）X≥55000 在爆破时，如果导火索燃烧的速度是0.015M/S，人跑开的速度是3M/S，那么要使点导火索的施工人员在点火后能够跑到100M以外（包括100M）的安全地区，这根导火索的长度至少应取多少M？解：设导火索长度为X米，则
X/0.015≥100/3
解得 X≥0.5
答：导火索的长度至少取0.5米。例2、某次个人象棋赛规定，赢１局得2分，平局得０分，负１局得－1分。在12局比赛中，积分超过15分，就可晋升到下一轮比赛。王明进了下一轮比赛，而且在全部12局比赛中，没有出现平局，问王明可能输了几局比赛？解：设他输了X局，则：
2(12-x)-x＞15
解得：X＜3
∵x应取自然数
∴X=0、1、2
答：王明可能输0或1或2局1、有一个两位数，个位数字与十位数字的和是 9，且这个两位数不小于72,求这个两位数。2、已知一种卡车每辆至多能载3吨货物，现有100吨黄豆，若要一次运完这批黄豆，至少需要这种卡车多少辆？3、为了保证长方形水闸闸门开启时的最大过水面积不少于90m2，如果闸门开启时的最大高度为5m，那么闸门的宽度至少为多少米？4、某企业向银行贷款1000万元，一年后归还银行贷款的本利1040万元，问年利率在怎样的一个范围内？上网计费方法：
计时制：3元/时；
包月制：50元/月，
另加1元/时生活中的数学方案一：3x方案二：x+50 某商场招聘某商品的促销员.促销员月工资的确定有以下两种方案:
(1)底薪600元,每销售一件商品加20元;
(2)底薪1000元,每销售一件商品加10元.问:促销员选择哪一种方案获得的工资多?请说明理由。生活中的数学解:设促销员每月可促销商品x件,由题意可得: 讨论：1、若方案一获得工资多，则有：600+20χ＞1000+10χ解得： χ>402、若两个方案获得的工资一样多，则有：600+20χ = 1000+10χ解得：χ=403、若方案二获得的工资多，则有600+20χ＜1000+10χ解得： χ< 40方案一、600+20χ
方案二、 1000+10χ