一元二次不等式的应用[上学期]

课件19张PPT。第五讲　一元二次不等式的应用一元二次方程、一元二次不等式均可用二次函数图象一统天下，但必须注意前后的等价易错题：
1、设集合A={x|－1≤x＜2},B={x|x＜a}，若A∩B≠Φ，则a的取值范围是（　）
A.a＜2　　　　　　 B.a＞－2　　　　
C.a＞－1　　　　　　D.－1＜a≤23、已知集合A={x| }
B={x|2≤x≤3a+1},求使A B的取值范围。2、已知集合A={x|x2+3x+2 ≥0}
B={x|mx2-4x+m-1＞0,m∈R}　若A∩B=φ,
A∪B=A,求m的取值范围绝对值不等式的基本方法：______
一元二次不等式的解法：
1、常规题的解法：__________
2、含有参数的二次不等式（明确身份）
1) x2-(3a+1)x+a(2a+1)＞0
2)x2-ax+1＞0
3)ax2-x+1＞01、已知集合M＝{x|(x―3)(x+1)≥0},
则M∩N等于（　）
A.R B.{x|―5C.{x|x<－5或―2P={x||x|A.01解决相关问题：
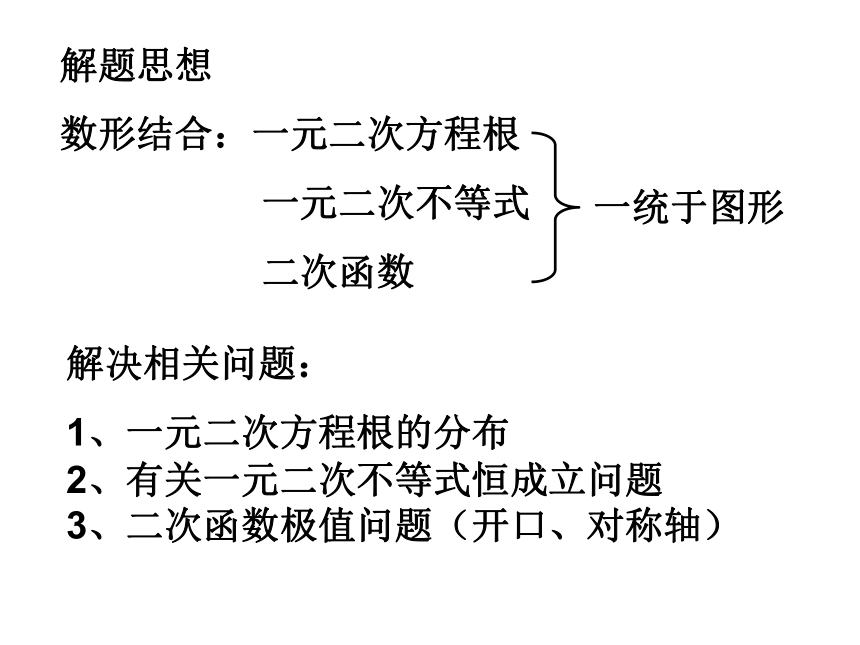
1、一元二次方程根的分布
2、有关一元二次不等式恒成立问题
3、二次函数极值问题（开口、对称轴）二次函数研究的几个方面：
1、开口 2、对称轴
3、顶点（最值） 4、与坐标轴的交点
注：研究二次函数的单调性、最值
必须研究清楚开口和对称轴。例题1、设函数f(x)=x2-x+a(a＞0)，
若f(n)＜0，则
A:f(n-1)＞0 B:f(n-1)＜0
C:f(n-1)=0 Df(n-1)与0的大小关系不确定例题2、已知二次函数f(x)=x2+ax+5对于任意t都有f(t)=f(-4-t)，且在闭区间[m,0]上有最大值5，有最小值1，则m的范围是
A　:m≤-2　　　　　　　B:-4≤m≤-2
C　:-2≤m≤0　　　　　　　D:-4≤m≤0变：二次函数f(x)的二次项系数为正，且对任意的实数x都有f(2+x)=f(2－x)。若f(1－2x2)（2）：若f(2a-x)=f(x)，则图象性质为:________
（3）：若f(a-x)=f(b+x)，则图象性质为:_______

小结上面三题：
（4）：若f(x+T)=f(x),T为非零常数，则图象具性
质为：_____________
（5）：若f(x+a)=f(x+b)，则图象性质为:_______例3、若方程7x2-(k+13)x+k2-k-2=0有两个不等的实数根x1,x2, 0＜x1＜1＜x2＜2，则实数k的取值范围是？变：关于x的不等式x2＋2mx＋m2―m/2―3/2＞0对一切正实数都成立，求实数m的取值范围。根的分布，数形结合分类讨论，确定标准练习：不等式 对满足1≤x≤3的一切x都成立，求实数m的取值范围。 分类讨论结构分析参数分离x2―2mx―1＞0 x2―2mx+m2+m-2＞0 例4、若关于x的不等式x2－ax+1≤0和ax2+x－1＞0均不成立，则（　）
A.a<－1/4或a≥2 B.－1/4≤a<2 C.―2≤a<―1/4 D. ―2 恒成立与不成立问题
变1：若不等式(a―2)x2+2(a―2)x―4<0对一切x∈R恒成立，则实数a的取值范围是（　）
A.(―∞，2] B.[―2,2]
C.(―2,2] D.(―∞,―2)
变2：x取一切实数 均可使有意义，则实数k的取值范围是（　）
A.k＜0或k＞3/4 B.0≤k＜3/4 C.0≤k≤3/4 D.k≥3/4变3、已知二次函数f(x)=2x2-(a-2)x-2a2-a若在区间[0,1]内至少存在一个实数b使得f(b)＞0则实数a的取值范围是
A：－2　 B:－1/2　
C:（－2，1） D:（－1/2，1）含有至多（至少）
等价 于 ≤（ ≥）正难则反例5：若ax2－2x＋a的值可取一切正实数，求实数a的取值范围。
变：函数y=lg(ax2 -2x+a)
①若定义域为R,则实数a的范围。
②若值域为R，则实数a的范围。分析：
R+是函数y=ax2-2x+a的值域的子集应用题6
某商人将进货单价为8元的商品按每件10元出售，每天可销售100个，现在它采取提高价格，减少进货量的办法增加利润。已知这种商品每件销售价提高1元，销售量就减少10件，问他将销售价定为多少，才能使每天赚的利润最大？综合题1：已知二次函数f(x)=ax2+bx+c的图象过点(－1,0),问是否存在常数a、b、c使不等式x≤f(x)≤(1+x2)/2对一切x∈R都成立。翻译条件、观察结构深挖隐含条件综合题2：已知抛物线y＝(m－1)x2＋(m－2)x－1
(m∈R).
⑴当m为何实数时，抛物线与x轴有两个交点？
⑵若关于x的方程(m－1)x2＋(m－2)x－1＝0的两个不等实数的倒数平方和不大于2，求实数m的取值范围；
⑶若抛物线与x轴交于两点A、B，与y轴交于点C，且ΔABC的面积等于2，试确定m的值。数学思想：
回顾基础、关注结构
数形结合、等价转化陈题回顾：变2：关于x的不等式 的解集是{x|4关注结构适时换元思考题：
已知关于x的不等式ax2+bx+a<0(ab>0)的解集为空集，则a2+b2-2b的取值范围？