二元一次不等式所表示的平面区域[上学期]
图片预览







文档简介
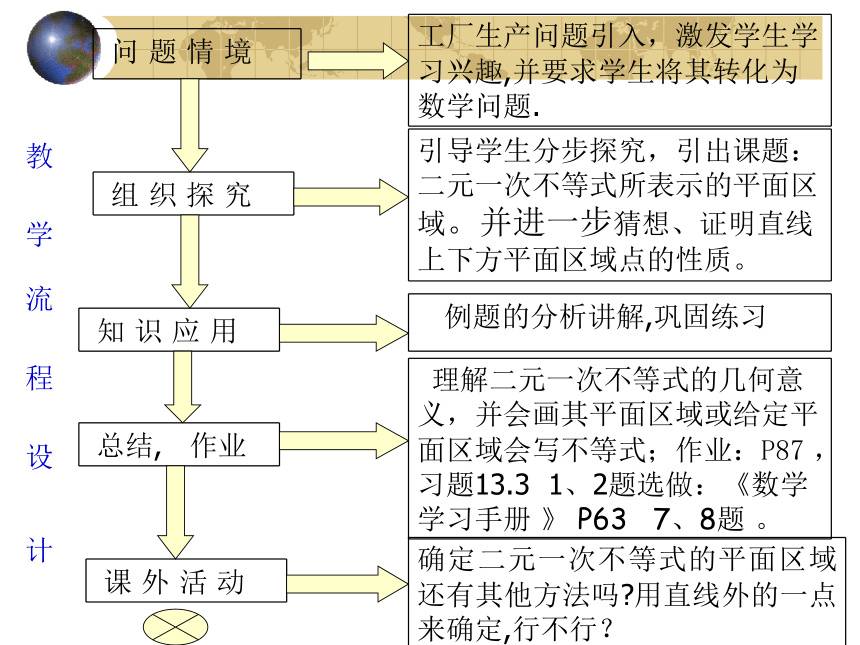
课件25张PPT。高中数学参赛课 教 学 流 程 设 计 一、问题情境我们来考察生产中遇到的一个问题:
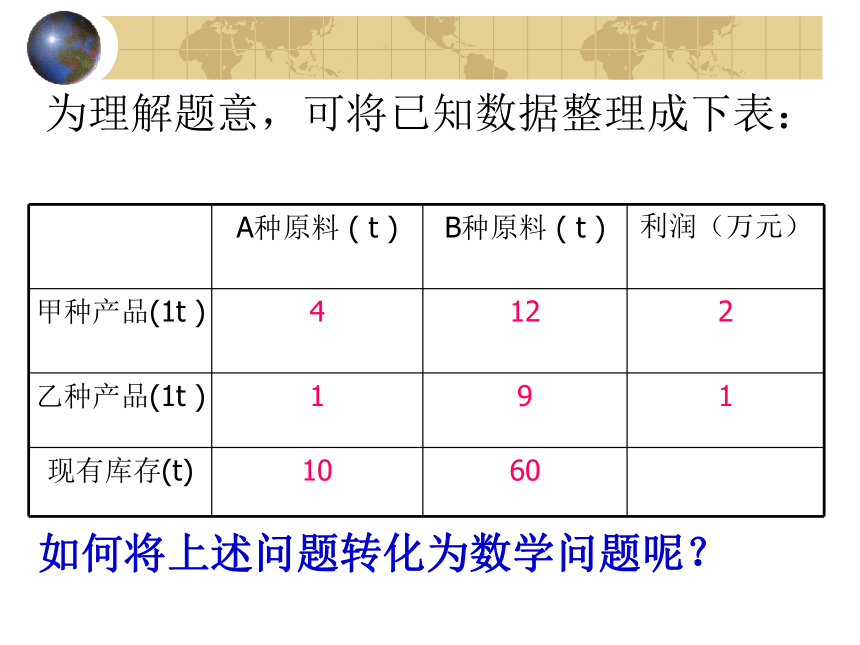
某工厂生产甲、乙两种新产品,生产1t甲种产品需要A种原料4t、B种原料12t,产生的利润为2万元;生产1t乙种产品需要A种原料10t 、B种原料9t,产生的利润1万元。现在有库存A种原料10t、B种原料60t,如何安排生产才能使利润最大?如何将上述问题转化为数学问题呢?为理解题意,可将已知数据整理成下表: 设计划生产甲、乙两种产品的吨数分别为 x,y,利润为P;根据题意,A、B两种原料分别不得超
10t,60t,即
4x+y≤10
12x+9y ≤60
x≥0
y ≥0这是一个二元一次不等式 组
(simultaneous binary linear inequalities)目标是使 P=2x+y 到达最大。 如何解决这个问题?我们分两步来求解上面的问题: 第一步 研究问题中的约束条件,得出 (x,y)的范围;? 二、建构数学第二步 在第一步得到的数对(x,y)的范围中找出使P达到最大的数对(x,y)。 今天我们重点研究第一步。问题1:上述问题中的约束条件都是以什么形式给出来的? 问题2:二元一次不等式有什么几何性质? 二元一次不等的解是一些数对(x,y),它的解集不能用数轴上的区间表示,而应是平面的一个区域。提示:一元一次不等的解集表示数轴上的
一个区间,如:3x≥6的解集为区间[2,+∞)问题3:二元一次不等式表示的平面区域上的点有什么性质?推广:一般地,直线 y=kx+b 把平面分成两个区域(如图13-3-1)
y>kx+b表示直线上方的平面区域;
yOxyy = kx+b下半平面
(y(y>kx+b)图13-3-1Oyy = kx+b下半平面
(y(y>kx+b)x(1)(2)试证明:二元一次不等式y>kx+b表示直线 : y=kx+b
上方的平面区域.
证明:首先,满足不等式y>kx+b的任意一点P(xp,yp)
(即满足yp >k xp +b)都在直线上方的平面区域内,这是
因为:过P点作PM⊥x轴,M为垂足,PM交 于Q(如图),
则Q的纵坐标为yQ=k xp +b.因为yp >k xp +b= yQ,所以
点P在Q的上方,即点P在直线 的上方.
其次,直线 y=kx+b上方的平面区域内的任一
点P(xp,yp),都满足不等式y>kx+b,这是因为P(xp,yp)在
直线 的上方.所以xp > yQ,即xp >k xp +b,这表明P(xp,yp)
满足不等式y>kx+b.
由上可知,不等式y>kx+b表示直线y=kx+b
上方的平面区域.Y=kx+boxyMQP(xp,yp)
··三、数学应用 1、例题
例1 画出下列不等式所表示的平面区域:
(1) y>-2x+1; (2) x-y+2>0.分析: y>kx+b表示直线上方的平面区域;
y将上式化为这两种形式。 那么先画出直线,
再找区域。Oxy(1)xy(2)图13-3-3解:y>-2x+1x-y+2>0O 例2 将下列图中的平面区域(阴影部分)用不等式表示出来(图13-3-4(1)中区域不包含y轴):xyxo(1)(2)(3)图13-3-4y=xoy6x+5y=22xoy 解:(1) x>0 (2) 6x+5y≤22 (3) y>x2练习
⑴ 判断下列命题是否正确:
①点(0,0)在平面区域x+y≥0内;
②点(0,1)在平面区域x-y+1<0内. (√ )(× )
(3).画出下列不等式所表示的平面区域:
①.y≤x-1; ②.x>2
③.y<0. (2).不等式x+4y-9≥0表示直线x+4y-9=0
A.上方平面区域 B.下方平面区域
C.上方平面区域 (包含直线)
D.下方平面区域 (包含直线) (C )
o1-1xyyxo2yx①②③(不包含x轴)解:●●
●o3、小结
(1)从实际情境中抽象出二元一次不等式组;
(2)了解二元一次不等式的几何意义,并会画其图;
(3)判断点是否在不等式所在的平面区域内。
4、作业:P87 (习题13.3) 1,2
选做:《数学学习手册》
P63 7、8题
课后练习:
试用选点法画出下列不等式的图象:
(1) x+y>2; (2) x-3y<0 确定二元一次不等式的平面区域还有
其他方法吗?用直线外的一点来确定,行不
行?如果行,请做以下练习:课后活动谢谢各位再见选点法: 直线Ax+By+C=0把平面分为两个区
域,对于同区域(同则)的所有点(x,y),
实数Ax+By+C的符号相同,所以只需在直
线某一则任取一点(x0,y0)代入Ax+By+C,
由A x0 +B y0 +C的符号即可判断出二元
一次不等式所在的区域。当C≠0时,
此点常选(0,0)二元一次不等式所表示的平面区域xy4x+y=10OOxy4x+y=10下半平面
(y<10-4x)上半平面
(y>10-4x)图13-3-2·0x·2x≥2图(1)oxyy=-x+1上半平面区域图(2)下半平面区域xyoY=kx+b (k>0)(x1,y1)(x1,y)(x1,y2)Y2>kx1 +bY1< kx1 +bxyo(x1,y1)(x1,y)(x1,y2)Y2>kx1 +bY1< kx1 +bY=kx+b
(k<0)(1)(2)上半平面下半平面上半平面下半平面······y2>y>y1 试写出证明
某工厂生产甲、乙两种新产品,生产1t甲种产品需要A种原料4t、B种原料12t,产生的利润为2万元;生产1t乙种产品需要A种原料10t 、B种原料9t,产生的利润1万元。现在有库存A种原料10t、B种原料60t,如何安排生产才能使利润最大?如何将上述问题转化为数学问题呢?为理解题意,可将已知数据整理成下表: 设计划生产甲、乙两种产品的吨数分别为 x,y,利润为P;根据题意,A、B两种原料分别不得超
10t,60t,即
4x+y≤10
12x+9y ≤60
x≥0
y ≥0这是一个二元一次不等式 组
(simultaneous binary linear inequalities)目标是使 P=2x+y 到达最大。 如何解决这个问题?我们分两步来求解上面的问题: 第一步 研究问题中的约束条件,得出 (x,y)的范围;? 二、建构数学第二步 在第一步得到的数对(x,y)的范围中找出使P达到最大的数对(x,y)。 今天我们重点研究第一步。问题1:上述问题中的约束条件都是以什么形式给出来的? 问题2:二元一次不等式有什么几何性质? 二元一次不等的解是一些数对(x,y),它的解集不能用数轴上的区间表示,而应是平面的一个区域。提示:一元一次不等的解集表示数轴上的
一个区间,如:3x≥6的解集为区间[2,+∞)问题3:二元一次不等式表示的平面区域上的点有什么性质?推广:一般地,直线 y=kx+b 把平面分成两个区域(如图13-3-1)
y>kx+b表示直线上方的平面区域;
y
(y
(y
上方的平面区域.
证明:首先,满足不等式y>kx+b的任意一点P(xp,yp)
(即满足yp >k xp +b)都在直线上方的平面区域内,这是
因为:过P点作PM⊥x轴,M为垂足,PM交 于Q(如图),
则Q的纵坐标为yQ=k xp +b.因为yp >k xp +b= yQ,所以
点P在Q的上方,即点P在直线 的上方.
其次,直线 y=kx+b上方的平面区域内的任一
点P(xp,yp),都满足不等式y>kx+b,这是因为P(xp,yp)在
直线 的上方.所以xp > yQ,即xp >k xp +b,这表明P(xp,yp)
满足不等式y>kx+b.
由上可知,不等式y>kx+b表示直线y=kx+b
上方的平面区域.Y=kx+boxyMQP(xp,yp)
··三、数学应用 1、例题
例1 画出下列不等式所表示的平面区域:
(1) y>-2x+1; (2) x-y+2>0.分析: y>kx+b表示直线上方的平面区域;
y
再找区域。Oxy(1)xy(2)图13-3-3解:y>-2x+1x-y+2>0O 例2 将下列图中的平面区域(阴影部分)用不等式表示出来(图13-3-4(1)中区域不包含y轴):xyxo(1)(2)(3)图13-3-4y=xoy6x+5y=22xoy 解:(1) x>0 (2) 6x+5y≤22 (3) y>x2练习
⑴ 判断下列命题是否正确:
①点(0,0)在平面区域x+y≥0内;
②点(0,1)在平面区域x-y+1<0内. (√ )(× )
(3).画出下列不等式所表示的平面区域:
①.y≤x-1; ②.x>2
③.y<0. (2).不等式x+4y-9≥0表示直线x+4y-9=0
A.上方平面区域 B.下方平面区域
C.上方平面区域 (包含直线)
D.下方平面区域 (包含直线) (C )
o1-1xyyxo2yx①②③(不包含x轴)解:●●
●o3、小结
(1)从实际情境中抽象出二元一次不等式组;
(2)了解二元一次不等式的几何意义,并会画其图;
(3)判断点是否在不等式所在的平面区域内。
4、作业:P87 (习题13.3) 1,2
选做:《数学学习手册》
P63 7、8题
课后练习:
试用选点法画出下列不等式的图象:
(1) x+y>2; (2) x-3y<0 确定二元一次不等式的平面区域还有
其他方法吗?用直线外的一点来确定,行不
行?如果行,请做以下练习:课后活动谢谢各位再见选点法: 直线Ax+By+C=0把平面分为两个区
域,对于同区域(同则)的所有点(x,y),
实数Ax+By+C的符号相同,所以只需在直
线某一则任取一点(x0,y0)代入Ax+By+C,
由A x0 +B y0 +C的符号即可判断出二元
一次不等式所在的区域。当C≠0时,
此点常选(0,0)二元一次不等式所表示的平面区域xy4x+y=10OOxy4x+y=10下半平面
(y<10-4x)上半平面
(y>10-4x)图13-3-2·0x·2x≥2图(1)oxyy=-x+1上半平面区域图(2)下半平面区域xyoY=kx+b (k>0)(x1,y1)(x1,y)(x1,y2)Y2>kx1 +bY1< kx1 +bxyo(x1,y1)(x1,y)(x1,y2)Y2>kx1 +bY1< kx1 +bY=kx+b
(k<0)(1)(2)上半平面下半平面上半平面下半平面······y2>y>y1 试写出证明
