扬州 线性规划[下学期]

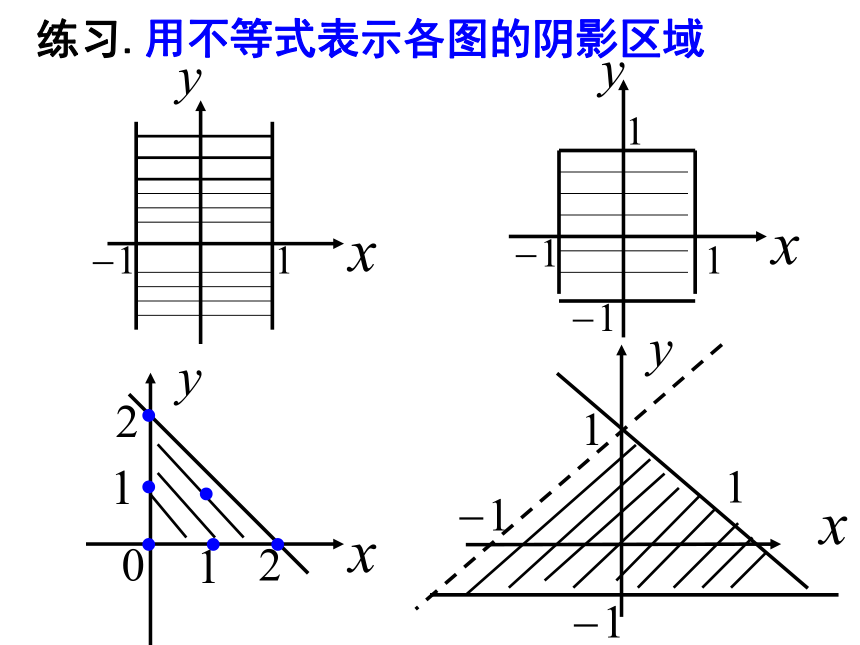
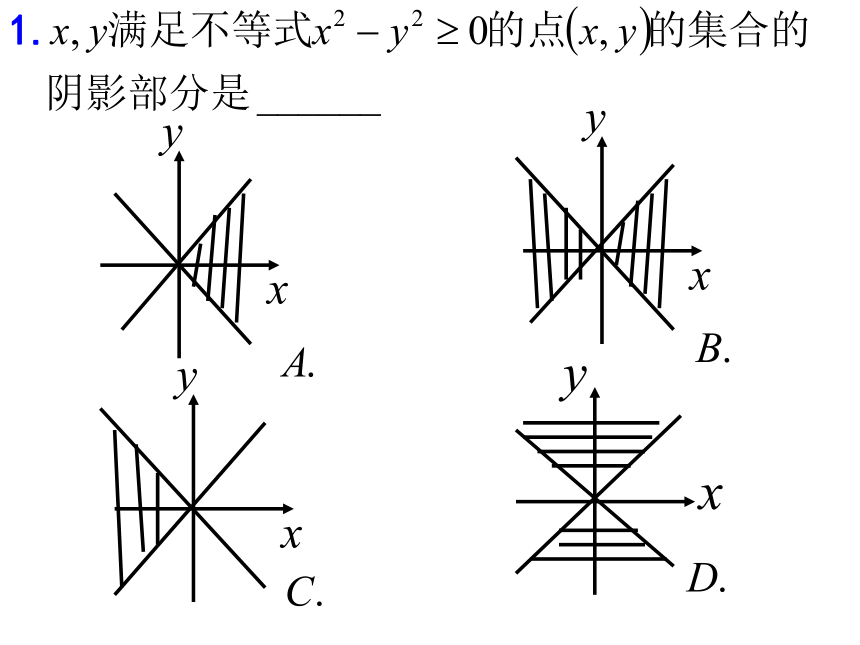
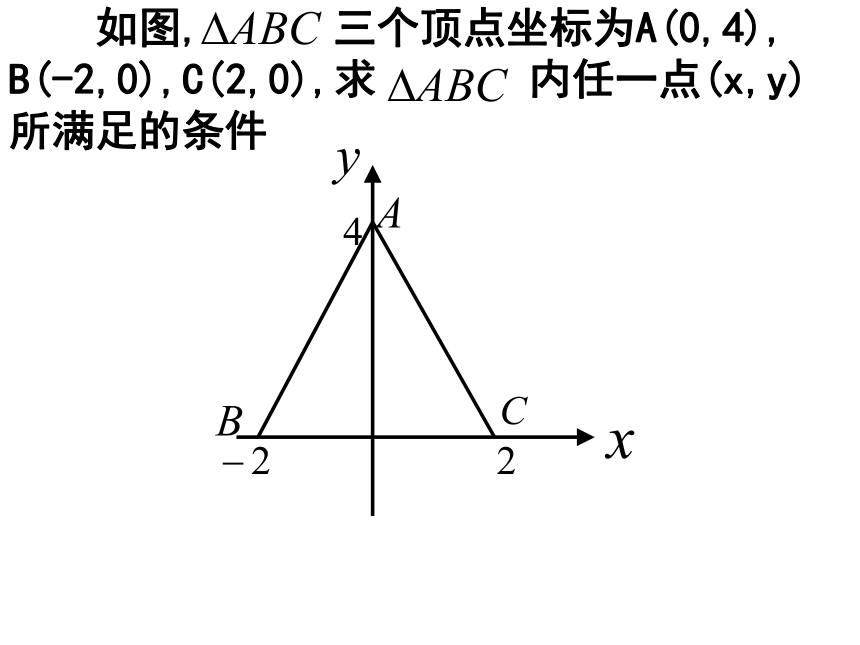
课件15张PPT。练习.用不等式表示各图的阴影区域练习(1)(2)(3)1. 如图, 三个顶点坐标为A(0,4),
B(-2,0),C(2,0),求 内任一点(x,y)
所满足的条件解线性规划问题的步骤： （1）画：画出线性约束条件所表示的可行域； （2）移：在线性目标函数所表示的一组平行线中，利用平移的方法找出与可行域有公共点且纵截距最大或最小的直线； （3）求：通过解方程组求出最优解； （4）答：作出答案。 已知直线l的方程是2x+3y=m,则xoy平面内，
m的几何意义是 ( )
A.直线l在y轴上的截距
B.直线l在y轴上的截距的3倍
C.直线l与y轴交点到原点距离的
D.直线l与x轴交点到原点距离的在直线方程ax+by+c=0中,保持a,b不变,当C
变化时可得到不同的直线,这些直线之间的
关系是________巩固练习:(1)求 的最大值,使式中的
满足约束条件(2)求 的最大值,使式中的
满足约束条件线性规划所求目标函数有三种类型:已知求 的最大值是求 的最值求 的最大值是已知求 的最大值是求 的整数解 例题1.某工厂制造A种电子装置45台,B种装置55台
,需用薄钢板给每台装置配一个外壳,已知薄钢板的
面积有两种规格,甲种薄钢板每张面积2m2,可做A,
B的外壳分别为3个和5个;乙种薄钢板每张面积3,
可做A,B的外壳各6个,求两种薄钢板各用多少张才
能使总的用料面积最小?解:设用两种薄钢板分别各用x,y,总的用料面积为z3526634555约束条件目标函数