【班海精品】人教版(新)七下-5.2 平行线及其判定 第一课时【优质课件】
文档属性
| 名称 | 【班海精品】人教版(新)七下-5.2 平行线及其判定 第一课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 9.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-09 17:35:23 | ||
图片预览









文档简介
(共49张PPT)
5.2 平行线及其判定
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
看一看,它们有什么共同之处?
扶手
铁轨
不相交
新课精讲
探索新知
1
知识点
平行线的定义
什么是平行线?
在同一平面内不相交的两条直线叫做平行线.
在同一平面内
注意
平行线体现三点:
不相交
两条直线
探索新知
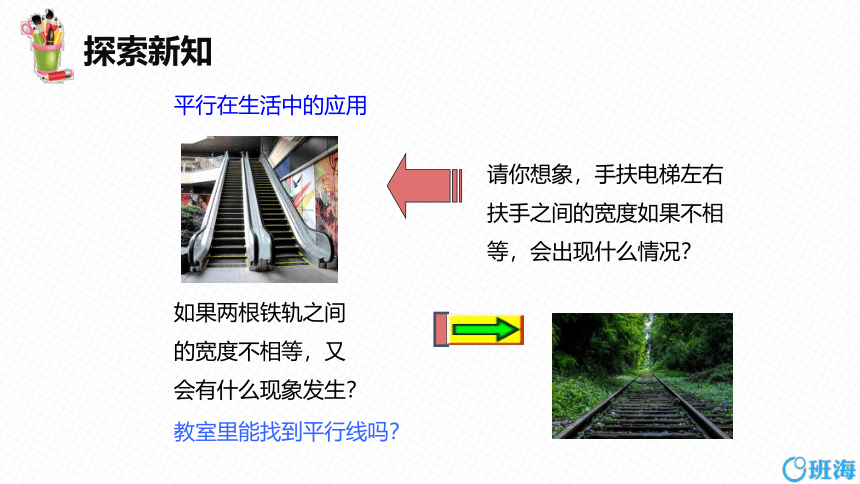
平行在生活中的应用
如果两根铁轨之间的宽度不相等,又会有什么现象发生?
请你想象,手扶电梯左右扶手之间的宽度如果不相等,会出现什么情况?
教室里能找到平行线吗?
探索新知
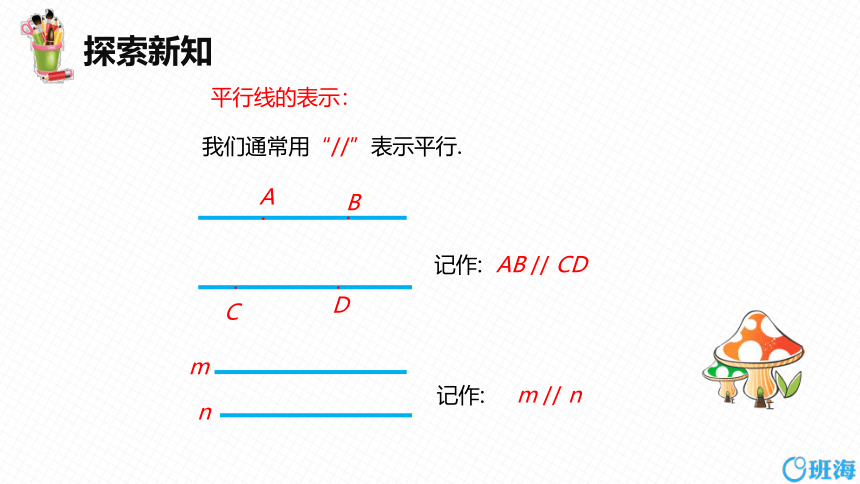
我们通常用“//”表示平行.
平行线的表示:
C
D
B
A
m
n
AB // CD
记作:
m // n
记作:
·
·
·
·
探索新知
例1 判断下列说法是否正确,并说明理由.
(1)不相交的两条直线是平行线;
(2)在同一平面内,两条不相交的线段是平行线.
导引: (1)没有强调两条直线在同一平面内;
(2)两条线段平行应该是这两条线段所在的直线平行.
(1)不正确;
理由:根据定义,它缺少了“在同一平面内”这一条件.
(2)不正确;
理由:定义中指出的是两条不相交的“直线”,而不是“线段”.
解:
探索新知
总 结
平行线的定义有三个特征:
一是在同一平面内;
二是不相交;
三是都是直线;三者缺一不可.
探索新知
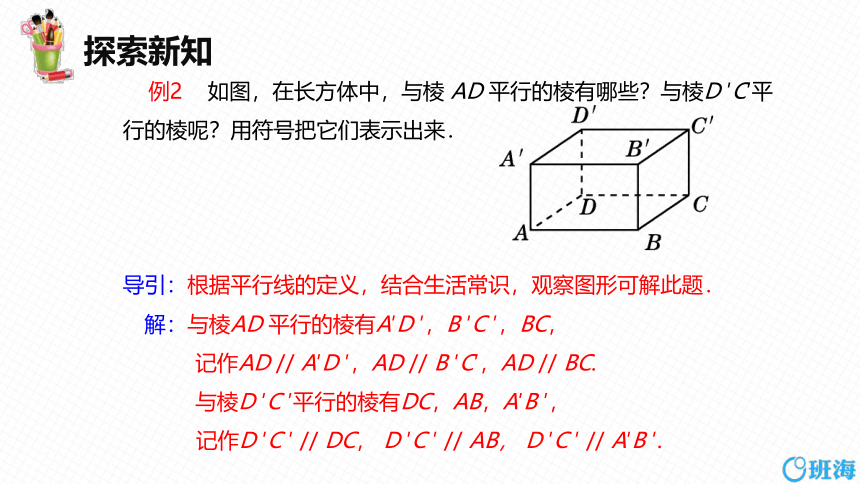
例2 如图,在长方体中,与棱 AD 平行的棱有哪些?与棱D ′C′平行的棱呢?用符号把它们表示出来.
导引:根据平行线的定义,结合生活常识,观察图形可解此题.
解:与棱AD 平行的棱有A′D ′,B ′C ′,BC,
记作AD // A′D ′,AD // B ′C′,AD // BC.
与棱D ′C ′平行的棱有DC,AB,A′B ′,
记作D ′C ′ // DC, D ′C ′ // AB, D ′C ′ // A′B ′.
探索新知
总 结
找平行线要注意两点:
(1)在同一平面内;
(2)不相交(无限延伸).
下列生活实例中,属于平行线的有( )
①交通路口的斑马线;
②黑板的上下边;
③百米直跑道的两边.
A.3个 B.2个
C.1个 D.0个
典题精讲
1
A
典题精讲
2
下列说法中,正确的有( )
①在同一平面内不相交的两条线段必平行;
②在同一平面内不相交的两条直线必平行;
③在同一平面内不平行的两条线段必相交;
④在同一平面内不平行的两条直线必相交.
A.1个 B.2个 C.3个 D.4个
B
典题精讲
3 如图,将一张长方形纸对折三次,则产生的折痕与折痕间的位置关系是( )
A.平行 B.垂直
C.平行或垂直 D.无法确定
C
典题精讲
a,b,c 是平面内任意三条直线,交点可以有( )
A.1个或2个或3个
B.0个或1个或2个或3个
C.1个或2个
D.以上都不对
4
B
典题精讲
如图,在长方体的各条棱中,与AB 平行的有____________________,与AB 相交的有 ,与AB 既不平行又不相交的有 .
5
CD、A1B1、C1D1
A1A、B1B、AD、BC
A1D1、B1C1、D1D、C1C
探索新知
2
知识点
平行线的画法
你会画平行线吗?
你能在方格纸中画出平行线吗?
b
a
d
c
n
m
t
探索新知
一放
二靠
三移
四画
画出这条直线的平行线
探索新知
过直线外一点画已知直线的平行线的步骤:
一落:把三角尺的一边落在已知直线上;
二靠:紧靠三角尺的另一边放一直尺;
三移:把这个三角尺沿着直尺移动使其经过已知点;
四画:沿三角尺的一边画直线.此直线即为已知直
线的平行线.
探索新知
例3 如图,过P 点作PQ∥AB 交BC 于Q,作PM ∥ AC 交AB 于M.
导引:过直线外一点画已知直线的平行线,
要按一“落”,二“靠”,三“移”,
四“画”的步骤进行.
解:如图.
A
B
C
P
探索新知
注意“移”时经过点的边是三角尺落在已知直线上的那一边,而不是任意一边,利用直尺和三角尺画过直线外一点的已知直线的平行线是几何画图的基本技能之一.
总 结
探索新知
例4 如图,在下面的网格中经过点C 画与线段AB 平行的直线 l1,再经过点B 画一条与线段AB 垂直的直线 l2.
解:如图.
探索新知
网格中作直线的平行线或垂线时,不需要借助尺规,直接根据网格的特点作图即可.
总 结
典题精讲
1
读下列语句,并画出图形:
(1)点P 是直线AB 外一点,直线CD 经过点P,且与直线AB 平行;
(2)直线AB,CD 是相交直线,点P 是直线AB,CD外的一点,直线EF经过点 P 且与直线AB 平行,与直线CD 相交于点E.
解:(1)如图(1)所示.
(2)如图(2)所示.
(1)
(2)
典题精讲
在如图所示的各图形中,过点M 画PQ∥AB.
2
解:略.
探索新知
3
知识点
平行线的确定性
经过点C 可以画几条直
线与直线AB 平行?
A
B
a
b
(2) 过点D 画一条直线与
AB 平行.
(3) 通过画图,你发现了什么?
经过直线外一点,有且只有一条直线与这条直线平行;
C
D
探索新知
下列说法:
①过一点有且只有一条直线与已知直线平行;
②一条直线的平行线只有一条;
③过直线外一点,有且只有一条直线与这条直线平行.
其中正确的有( )
A.3个 B.2个 C.1个 D.0个
过直线外一点可以画一条直线与已知直线平行,
而过直线上一点画不出与该直线平行的直线;
一条直线的平行线有无数条,故只有③正确.
C
例5
导引:
探索新知
对于此类辨析题,要正确解答,必须要抓住相关的内容,特别是关键字词及其重要特征,要在比较中理解,再在理解的基础上进行记忆.
总 结
典题精讲
如图,当风车的一片叶子AB 旋转到与地面MN 平行时,叶子CD 所在的直线与地面MN________,理由是 ______________________________ ____ _____________.
1
相交
经过直线外一点,有且只有一条直线与这条直线平行
典题精讲
已知直线AB 和一点P,过点P 画直线AB 的平行线,可画( )
A.1条 B.0条
C.1条或0条 D.无数条
2
C
探索新知
4
知识点
平行线的传递性
平行公理的推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行.简称:同平行于第三条直线的两直线平行.
表达方式:如果a∥c,b ∥ c,那么a ∥ b.
平行公理的推论:可用来判定两直线平行.
探索新知
如图,P 是三角形ABC 内部的任意一点.
(1)过P 点向左画射线PM∥BC 交AB 于点M,过P 点向右画射线PN ∥ BC 交AC 于点N;
(2)在(1)中画出的图形中,∠MPN 的度数一定等于180°,你能说明其中的道理吗?
例6
探索新知
在(1)中,按照过直线外一点画已知直线的平行线的方法画图即可.在(2)中,要说明∠MPN=180°,可转化为说明点M, P, N 在同一条直线上.
(1)画出的射线PM,PN,如上页图.
(2)因为射线PM∥BC,射线PN ∥ BC,所以直线PM ∥ BC,直线PN ∥ BC.所以直线PM 与直线PN 是同一条直线(过直线外一点有且只有一条直线与这条直线平行),即点M, P, N 在同一条直线上.所以∠MPN=180°.
导引:
解:
本题运用转化思想,把说明∠MPN=180°转化为说明点M,P,N 在同一条直线上,进而把问题转化为利用有关平行线的基本事实说明直线PM 与直线PN 是同一条直线.
总 结
典题精讲
三条直线l1,l2,l3,若l1 ∥ l3,l2 ∥ l3,则l1与l2的位置关系是( )
A.l1与l2相交
B.l1与l2平行
C.l1与l2相交或l1与l2平行
D.无法确定
1
B
典题精讲
下列说法中,错误的有( )
①若a 与c 相交,b 与c 相交,则a 与b 相交;
②若a∥b,b ∥ c,则a ∥ c;
③过直线外一点有且只有一条直线与已知直线平行;
④在同一平面内,两条直线的位置关系有平行、相交、垂直三种.
A.3个 B.2个 C.1个 D.0个
2
B
易错提醒
下列说法正确的是( )
A.两条不相交的直线叫做平行线
B.过一点有且只有一条直线与已知直线平行
C.在同一平面内不相交的两条线段互相平行
D.在同一平面内不相交的两条直线叫做平行线
D
易错点:对平行线的定义理解不透彻而出错.
学以致用
小试牛刀
在同一平面内,直线m,n 相交于点O,且l∥n,则直线l和m 的关系是( )
A.平行 B.相交
C.重合 D.以上都有可能
B
1
小试牛刀
如图,(1)过BC上任意一点P (不与B,C 重合)画AB 的平行线交AC 于T;
(2)过点C 画MN∥AB;
(3)直线PT,MN 具有何种位置关系?试说明理由.
解:
(1) (2)如图.
(3)PT∥MN,理由如下:因为PT ∥ AB,
MN ∥ AB,所以PT ∥ MN.
2
小试牛刀
如图,如果CD∥AB,CE ∥ AB,那么C,D,E 三点是否共线?你能说明理由吗?
解:
C,D,E 三点共线,理由如下:经过直线外一点,有且只有一条直线与已知直线平行.
3
小试牛刀
(1)画∠AOB=60°,在∠AOB 内任取一点P,过点P 作直线CD∥AO,再过点P 作直线EF ∥ OB;
(2)测量∠CPE,∠EPD,∠DPF,∠CPF 的度数.
(1)这些角的边与∠AOB 的边有何位置关系?
(2)这些角的度数与∠AOB 的度数之间存在什么关系?
把你的发现用一句话概括出来.
实践:
探究:
发现:
小试牛刀
解:
实践:(1)如图所示.
(2)∠CPE=120°,∠EPD=60°,∠DPF=120°,
∠CPF=60°.
探究:(1)平行.(2)相等或互补.
发现:如果两个角的两边分别平行,
那么这两个角相等或互补.
小试牛刀
先阅读,然后解答.
问题:两条直线将平面分成几部分?
解:如图①,两条直线平行时,它们将平面分成三部分;
如图②,两条直线不平行时,它们将平面分成四部分.
根据上述内容,解答下面的问题.
4
小试牛刀
(1)上面问题的解题过程应用了________的数学思想(填“转化”“分类”或“整体处理”);
(2)三条直线将平面分成几部分?
解:
(2)如图,三条直线可以将平面分成四或六或七部分.
分类
课堂小结
课堂小结
1. 平行线的定义及平面内两直线的位置关系
平行线的定义包含缺一不可的三个条件:
①在同一平面内;②不相交;③都是直线.
2. 平行线的画法
一落、二靠、三移、四画
3. 平行线的基本事实及其推论
(1)“有且只有”强调直线的存在性和唯一性;
(2)前提条件“经过直线外一点”,若点在直线上,不可能有平行线.
4. 平行线具有传递性.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
5.2 平行线及其判定
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
看一看,它们有什么共同之处?
扶手
铁轨
不相交
新课精讲
探索新知
1
知识点
平行线的定义
什么是平行线?
在同一平面内不相交的两条直线叫做平行线.
在同一平面内
注意
平行线体现三点:
不相交
两条直线
探索新知
平行在生活中的应用
如果两根铁轨之间的宽度不相等,又会有什么现象发生?
请你想象,手扶电梯左右扶手之间的宽度如果不相等,会出现什么情况?
教室里能找到平行线吗?
探索新知
我们通常用“//”表示平行.
平行线的表示:
C
D
B
A
m
n
AB // CD
记作:
m // n
记作:
·
·
·
·
探索新知
例1 判断下列说法是否正确,并说明理由.
(1)不相交的两条直线是平行线;
(2)在同一平面内,两条不相交的线段是平行线.
导引: (1)没有强调两条直线在同一平面内;
(2)两条线段平行应该是这两条线段所在的直线平行.
(1)不正确;
理由:根据定义,它缺少了“在同一平面内”这一条件.
(2)不正确;
理由:定义中指出的是两条不相交的“直线”,而不是“线段”.
解:
探索新知
总 结
平行线的定义有三个特征:
一是在同一平面内;
二是不相交;
三是都是直线;三者缺一不可.
探索新知
例2 如图,在长方体中,与棱 AD 平行的棱有哪些?与棱D ′C′平行的棱呢?用符号把它们表示出来.
导引:根据平行线的定义,结合生活常识,观察图形可解此题.
解:与棱AD 平行的棱有A′D ′,B ′C ′,BC,
记作AD // A′D ′,AD // B ′C′,AD // BC.
与棱D ′C ′平行的棱有DC,AB,A′B ′,
记作D ′C ′ // DC, D ′C ′ // AB, D ′C ′ // A′B ′.
探索新知
总 结
找平行线要注意两点:
(1)在同一平面内;
(2)不相交(无限延伸).
下列生活实例中,属于平行线的有( )
①交通路口的斑马线;
②黑板的上下边;
③百米直跑道的两边.
A.3个 B.2个
C.1个 D.0个
典题精讲
1
A
典题精讲
2
下列说法中,正确的有( )
①在同一平面内不相交的两条线段必平行;
②在同一平面内不相交的两条直线必平行;
③在同一平面内不平行的两条线段必相交;
④在同一平面内不平行的两条直线必相交.
A.1个 B.2个 C.3个 D.4个
B
典题精讲
3 如图,将一张长方形纸对折三次,则产生的折痕与折痕间的位置关系是( )
A.平行 B.垂直
C.平行或垂直 D.无法确定
C
典题精讲
a,b,c 是平面内任意三条直线,交点可以有( )
A.1个或2个或3个
B.0个或1个或2个或3个
C.1个或2个
D.以上都不对
4
B
典题精讲
如图,在长方体的各条棱中,与AB 平行的有____________________,与AB 相交的有 ,与AB 既不平行又不相交的有 .
5
CD、A1B1、C1D1
A1A、B1B、AD、BC
A1D1、B1C1、D1D、C1C
探索新知
2
知识点
平行线的画法
你会画平行线吗?
你能在方格纸中画出平行线吗?
b
a
d
c
n
m
t
探索新知
一放
二靠
三移
四画
画出这条直线的平行线
探索新知
过直线外一点画已知直线的平行线的步骤:
一落:把三角尺的一边落在已知直线上;
二靠:紧靠三角尺的另一边放一直尺;
三移:把这个三角尺沿着直尺移动使其经过已知点;
四画:沿三角尺的一边画直线.此直线即为已知直
线的平行线.
探索新知
例3 如图,过P 点作PQ∥AB 交BC 于Q,作PM ∥ AC 交AB 于M.
导引:过直线外一点画已知直线的平行线,
要按一“落”,二“靠”,三“移”,
四“画”的步骤进行.
解:如图.
A
B
C
P
探索新知
注意“移”时经过点的边是三角尺落在已知直线上的那一边,而不是任意一边,利用直尺和三角尺画过直线外一点的已知直线的平行线是几何画图的基本技能之一.
总 结
探索新知
例4 如图,在下面的网格中经过点C 画与线段AB 平行的直线 l1,再经过点B 画一条与线段AB 垂直的直线 l2.
解:如图.
探索新知
网格中作直线的平行线或垂线时,不需要借助尺规,直接根据网格的特点作图即可.
总 结
典题精讲
1
读下列语句,并画出图形:
(1)点P 是直线AB 外一点,直线CD 经过点P,且与直线AB 平行;
(2)直线AB,CD 是相交直线,点P 是直线AB,CD外的一点,直线EF经过点 P 且与直线AB 平行,与直线CD 相交于点E.
解:(1)如图(1)所示.
(2)如图(2)所示.
(1)
(2)
典题精讲
在如图所示的各图形中,过点M 画PQ∥AB.
2
解:略.
探索新知
3
知识点
平行线的确定性
经过点C 可以画几条直
线与直线AB 平行?
A
B
a
b
(2) 过点D 画一条直线与
AB 平行.
(3) 通过画图,你发现了什么?
经过直线外一点,有且只有一条直线与这条直线平行;
C
D
探索新知
下列说法:
①过一点有且只有一条直线与已知直线平行;
②一条直线的平行线只有一条;
③过直线外一点,有且只有一条直线与这条直线平行.
其中正确的有( )
A.3个 B.2个 C.1个 D.0个
过直线外一点可以画一条直线与已知直线平行,
而过直线上一点画不出与该直线平行的直线;
一条直线的平行线有无数条,故只有③正确.
C
例5
导引:
探索新知
对于此类辨析题,要正确解答,必须要抓住相关的内容,特别是关键字词及其重要特征,要在比较中理解,再在理解的基础上进行记忆.
总 结
典题精讲
如图,当风车的一片叶子AB 旋转到与地面MN 平行时,叶子CD 所在的直线与地面MN________,理由是 ______________________________ ____ _____________.
1
相交
经过直线外一点,有且只有一条直线与这条直线平行
典题精讲
已知直线AB 和一点P,过点P 画直线AB 的平行线,可画( )
A.1条 B.0条
C.1条或0条 D.无数条
2
C
探索新知
4
知识点
平行线的传递性
平行公理的推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行.简称:同平行于第三条直线的两直线平行.
表达方式:如果a∥c,b ∥ c,那么a ∥ b.
平行公理的推论:可用来判定两直线平行.
探索新知
如图,P 是三角形ABC 内部的任意一点.
(1)过P 点向左画射线PM∥BC 交AB 于点M,过P 点向右画射线PN ∥ BC 交AC 于点N;
(2)在(1)中画出的图形中,∠MPN 的度数一定等于180°,你能说明其中的道理吗?
例6
探索新知
在(1)中,按照过直线外一点画已知直线的平行线的方法画图即可.在(2)中,要说明∠MPN=180°,可转化为说明点M, P, N 在同一条直线上.
(1)画出的射线PM,PN,如上页图.
(2)因为射线PM∥BC,射线PN ∥ BC,所以直线PM ∥ BC,直线PN ∥ BC.所以直线PM 与直线PN 是同一条直线(过直线外一点有且只有一条直线与这条直线平行),即点M, P, N 在同一条直线上.所以∠MPN=180°.
导引:
解:
本题运用转化思想,把说明∠MPN=180°转化为说明点M,P,N 在同一条直线上,进而把问题转化为利用有关平行线的基本事实说明直线PM 与直线PN 是同一条直线.
总 结
典题精讲
三条直线l1,l2,l3,若l1 ∥ l3,l2 ∥ l3,则l1与l2的位置关系是( )
A.l1与l2相交
B.l1与l2平行
C.l1与l2相交或l1与l2平行
D.无法确定
1
B
典题精讲
下列说法中,错误的有( )
①若a 与c 相交,b 与c 相交,则a 与b 相交;
②若a∥b,b ∥ c,则a ∥ c;
③过直线外一点有且只有一条直线与已知直线平行;
④在同一平面内,两条直线的位置关系有平行、相交、垂直三种.
A.3个 B.2个 C.1个 D.0个
2
B
易错提醒
下列说法正确的是( )
A.两条不相交的直线叫做平行线
B.过一点有且只有一条直线与已知直线平行
C.在同一平面内不相交的两条线段互相平行
D.在同一平面内不相交的两条直线叫做平行线
D
易错点:对平行线的定义理解不透彻而出错.
学以致用
小试牛刀
在同一平面内,直线m,n 相交于点O,且l∥n,则直线l和m 的关系是( )
A.平行 B.相交
C.重合 D.以上都有可能
B
1
小试牛刀
如图,(1)过BC上任意一点P (不与B,C 重合)画AB 的平行线交AC 于T;
(2)过点C 画MN∥AB;
(3)直线PT,MN 具有何种位置关系?试说明理由.
解:
(1) (2)如图.
(3)PT∥MN,理由如下:因为PT ∥ AB,
MN ∥ AB,所以PT ∥ MN.
2
小试牛刀
如图,如果CD∥AB,CE ∥ AB,那么C,D,E 三点是否共线?你能说明理由吗?
解:
C,D,E 三点共线,理由如下:经过直线外一点,有且只有一条直线与已知直线平行.
3
小试牛刀
(1)画∠AOB=60°,在∠AOB 内任取一点P,过点P 作直线CD∥AO,再过点P 作直线EF ∥ OB;
(2)测量∠CPE,∠EPD,∠DPF,∠CPF 的度数.
(1)这些角的边与∠AOB 的边有何位置关系?
(2)这些角的度数与∠AOB 的度数之间存在什么关系?
把你的发现用一句话概括出来.
实践:
探究:
发现:
小试牛刀
解:
实践:(1)如图所示.
(2)∠CPE=120°,∠EPD=60°,∠DPF=120°,
∠CPF=60°.
探究:(1)平行.(2)相等或互补.
发现:如果两个角的两边分别平行,
那么这两个角相等或互补.
小试牛刀
先阅读,然后解答.
问题:两条直线将平面分成几部分?
解:如图①,两条直线平行时,它们将平面分成三部分;
如图②,两条直线不平行时,它们将平面分成四部分.
根据上述内容,解答下面的问题.
4
小试牛刀
(1)上面问题的解题过程应用了________的数学思想(填“转化”“分类”或“整体处理”);
(2)三条直线将平面分成几部分?
解:
(2)如图,三条直线可以将平面分成四或六或七部分.
分类
课堂小结
课堂小结
1. 平行线的定义及平面内两直线的位置关系
平行线的定义包含缺一不可的三个条件:
①在同一平面内;②不相交;③都是直线.
2. 平行线的画法
一落、二靠、三移、四画
3. 平行线的基本事实及其推论
(1)“有且只有”强调直线的存在性和唯一性;
(2)前提条件“经过直线外一点”,若点在直线上,不可能有平行线.
4. 平行线具有传递性.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
