【班海精品】人教版(新)七下-5.2 平行线及其判定 第二课时【优质课件】
文档属性
| 名称 | 【班海精品】人教版(新)七下-5.2 平行线及其判定 第二课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-09 00:00:00 | ||
图片预览






文档简介
(共35张PPT)
5.2 平行线及其判定
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
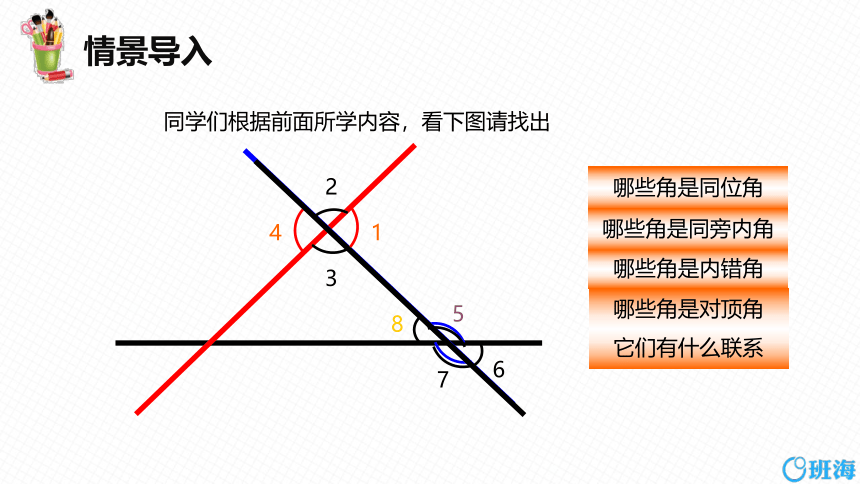
同学们根据前面所学内容,看下图请找出
哪些角是内错角
哪些角是同位角
哪些角是同旁内角
哪些角是对顶角
它们有什么联系
2
3
4
1
5
7
8
6
新课精讲
探索新知
1
知识点
由“同位角相等”判定两直线平行
思考
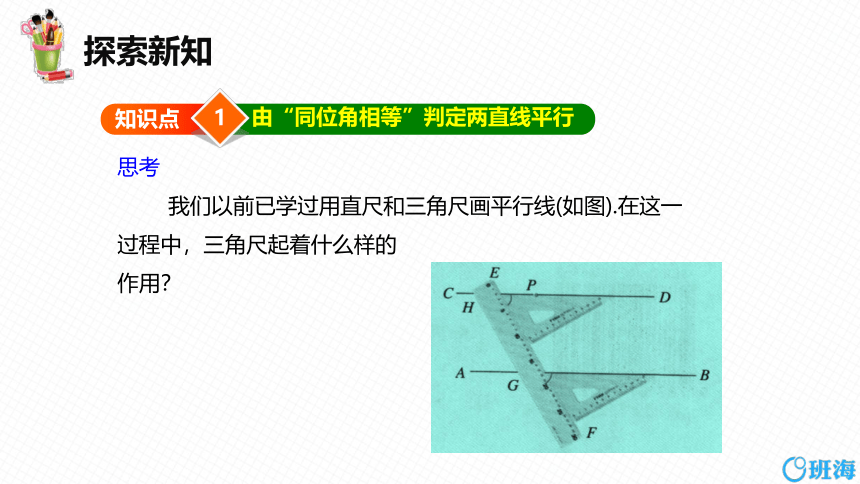
我们以前已学过用直尺和三角尺画平行线(如图).在这一过程中,三角尺起着什么样的
作用?
探索新知
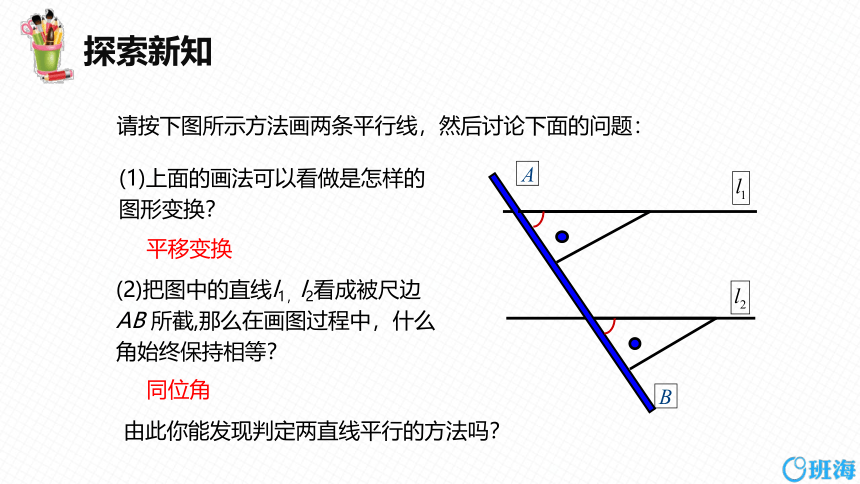
请按下图所示方法画两条平行线,然后讨论下面的问题:
(1)上面的画法可以看做是怎样的图形变换?
(2)把图中的直线l1,l2看成被尺边AB 所截,那么在画图过程中,什么角始终保持相等?
平移变换
同位角
由此你能发现判定两直线平行的方法吗?
探索新知
一般地,判断两直线平行有下面的方法:
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单地说,同位角相等,两直线平行.
探索新知
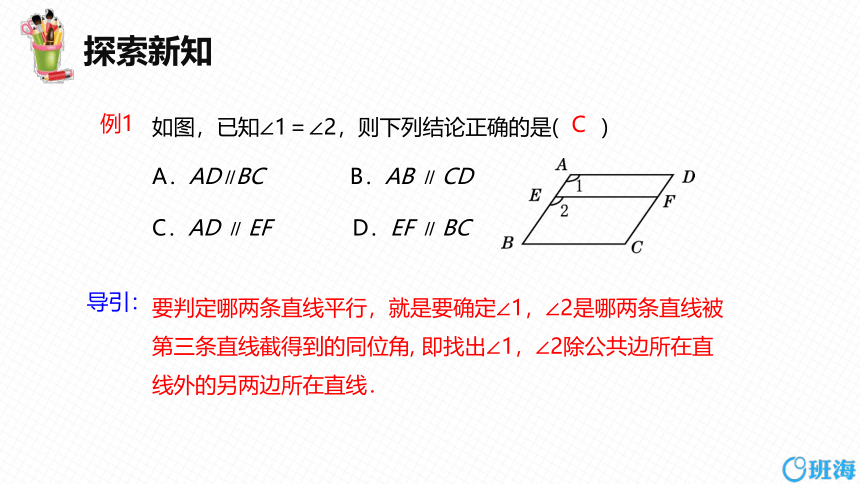
如图,已知∠1=∠2,则下列结论正确的是( )
A.AD∥BC B.AB ∥ CD
C.AD ∥ EF D.EF ∥ BC
要判定哪两条直线平行,就是要确定∠1,∠2是哪两条直线被第三条直线截得到的同位角, 即找出∠1,∠2除公共边所在直线外的另两边所在直线.
C
导引:
例1
探索新知
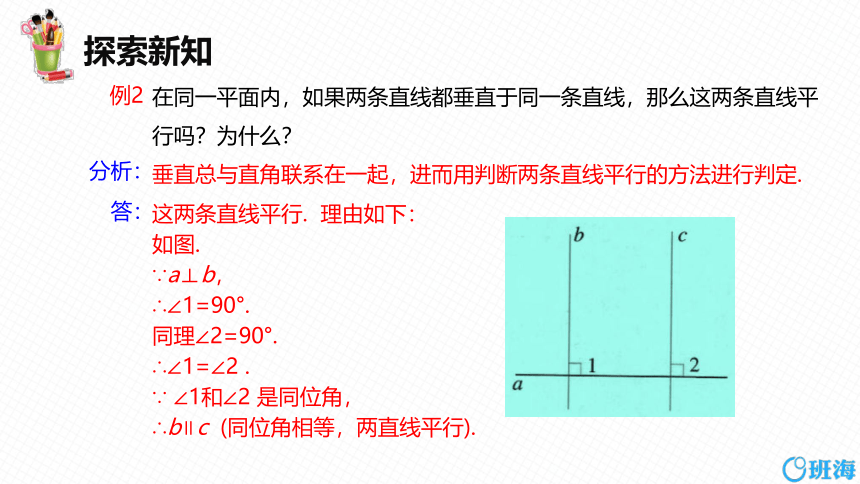
在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
垂直总与直角联系在一起,进而用判断两条直线平行的方法进行判定.
例2
分析:
这两条直线平行. 理由如下:
如图.
∵a⊥b,
∴∠1=90°.
同理∠2=90°.
∴∠1=∠2 .
∵ ∠1和∠2 是同位角,
∴b∥c (同位角相等,两直线平行).
答:
探索新知
总 结
判断两条直线是否平行,可以找出这两条直线被第三条直线所截得到的一对同位角,并利用相关角的条件判断其是否相等,如果相等,那么这两条直线平行.
典题精讲
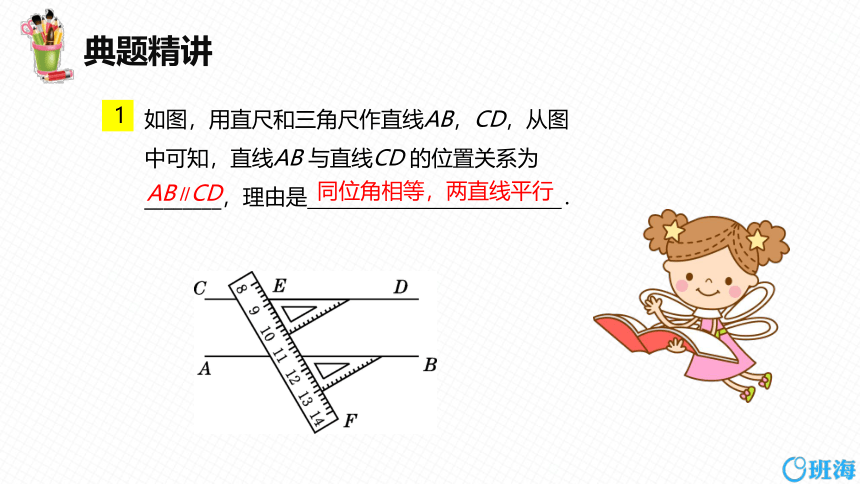
如图,用直尺和三角尺作直线AB,CD,从图中可知,直线AB 与直线CD 的位置关系为________,理由是 .
1
AB∥CD
同位角相等,两直线平行
典题精讲
如图,直线AB,CD 被直线EF 所截,∠1=55°,下列条件中能判定AB∥CD的是( )
A.∠2=35°
B.∠2=45°
C.∠2=55°
D.∠2=125°
2
C
典题精讲
如图,能判定EB∥AC 的条件是( )
A.∠C=∠ABE
B.∠A=∠EBD
C.∠C=∠ABC
D.∠C=∠EBD
3
D
典题精讲
如图,已知∠1=∠2,则下列结论正确的是( )
A.AD ∥ BC
B.AB ∥ CD
C.AD ∥ EF
D.EF ∥ BC
4
C
探索新知
2
知识点
由“第三直线”判定两直线平行
如图,你能说出木工用图中的角尺画平行线的道理吗
探索新知
总 结
平行于同一条直线的两直线平行.
探索新知
如图所示,直线AB、CD 是一条河的两岸,并AB∥CD,点E 为直线AB、CD 外一点.现想过点E 作CD 的平行线,则只需过点E 作岸AB 的平行线即可.其理由是什么
例3
探索新知
利用平行线的性质,把实际问题转化为数学
问题回答.
解:
分析:
理由是(1)过直线外一点有且只有一条直线与
已知直线平行.(2)如果两条直线都与第三条
直线平行,那么这两条直线也互相平行.
探索新知
总 结
在同一平面内和一条直线平行的直线也互相平行.
典题精讲
如图,木工师傅利用直角尺在木板上画出两条线段,则线段AB______CD.
1
∥
典题精讲
在每一步推理后面的括号内填上理由.
(1)如图①,因为AB∥CD,EF∥CD,
所以AB∥EF ( ).
(2)如图②,因为AB∥CD,过点F 作EF∥AB
( ) ,
所以EF∥CD ( ).
2
平行于同一直线的两条直线平行
过直线外一点,有且只有一条直线与这条直线平行
平行于同一直线的两条直线平行
典题精讲
在同一个平面内,不重合的两个直角,如果它们有一条边共线,那么另一条边( )
A.互相平行 B.互相垂直
C.共线 D.互相平行或共线
3
D
易错提醒
如图,已知AB⊥BD 于点B,CD⊥BD 于点D,
∠1=∠2,试问CD 与EF 平行吗?为什么?
解:CD∥EF.理由:因为∠1=∠2(__________),
所以AB∥EF(______________________________).
因为AB⊥BD,CD⊥BD,
所以AB∥CD (____________________ _______ __________).
所以CD∥EF(______________ _____________________).
已知
同位角相等,两直线平行
平行于同一条直线的两条直线互相平行
在同一平面内,垂直于同一条直线的两条直线互相平行
易错点:填错理由而致错.
学以致用
小试牛刀
如图,CD 平分∠ACE,且∠B=∠ACD,可以得出的结论是( )
A.AD∥BC
B.AB ∥ CD
C.CA平分∠BCD
D.AC平分∠BAD
B
1
小试牛刀
三条直线a,b,c,若a∥c,b∥c,则a 与b 的位置关系是( )
A.a⊥b B.a∥b
C.a⊥b或a∥b D.无法确定
2
B
小试牛刀
如图,点B 在DC上,BE 平分∠ABD,
∠ABE=∠C,试说明:BE∥AC.
解:因为BE 平分∠ABD,
所以∠ABE=∠DBE (___________________).
因为∠ABE=∠C,
所以∠DBE=∠C.
所以BE∥AC (__________________________).
角平分线的定义
同位角相等,两直线平行
3
小试牛刀
如图,已知∠1=68°,∠2=68°,∠3=112°.
(1)因为∠1=68°,∠2=68°(已知),
所以∠1=∠2.
所以______ ∥ ______(同位角相等,两直线平行)
(2)因为∠3+∠4=180°(邻补角的定义),∠3=112°,
所以∠4=68°.
又因为∠2=68°,
所以∠2=∠4.
所以______ ∥ ______(同位角相等,两直线平行).
a
b
b
c
4
小试牛刀
如图,已知直线a,b,c,d,e,且∠1=∠2,∠3=
∠4,则a 与c 平行吗?为什么?
解:a 与c 平行.
理由:因为∠1=∠2(__________),
所以a∥b(________________ ________).
因为∠3=∠4(__________________),
所以b∥c (____________ _____________).
所以a∥c (______ __________________________).
已知
同位角相等,两直线平行
已知
同位角相等,两直线平行
平行于同一条直线的两条直线平行
5
小试牛刀
如图,已知∠1=90°,∠2=90°,试说明:CD∥EF.
(1)方法一:用“同位角相等”说明;
(2)方法二:用“第三直线”说明.
(1)方法一:因为∠1=90°,∠2=90°,
所以∠1=∠2.所以CD∥EF.
(2)方法二:因为∠1=90°,∠2=90°,
所以CD⊥AB,EF⊥AB.
所以CD∥EF.
6
小试牛刀
在同一平面内,已知A,B,C 是直线l 同旁的三个点.
(1)若AB∥l,BC∥l,则A,B,C 三点在同一条直线上吗?为什么?
(2)若AB⊥l,BC⊥l,则A,B,C 三点在同一条直线上吗?为什么?
解:
(1)在同一条直线上.理由:因为直线AB,BC 都经过点B,且都与直线l 平行,而过直线外一点有且只有一条直线与这条直线平行,所以AB,BC为同一条直线,所以A,B,C 三点在同一条直线上.
(2)在同一条直线上.理由:因为直线AB,BC 都经过点B,且都与直线l垂直,而在同一平面内,过一点有且只有一条直线与已知直线垂直,所以AB,BC 为同一条直线,所以A,B,C 三点在同一条直线上.
7
课堂小结
课堂小结
判定两直线平行的方法:
(1)利用平行线的定义判定;
(2)利用“同位角相等,两直线平行”判定;
(3)利用“第三直线”判定.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
5.2 平行线及其判定
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
同学们根据前面所学内容,看下图请找出
哪些角是内错角
哪些角是同位角
哪些角是同旁内角
哪些角是对顶角
它们有什么联系
2
3
4
1
5
7
8
6
新课精讲
探索新知
1
知识点
由“同位角相等”判定两直线平行
思考
我们以前已学过用直尺和三角尺画平行线(如图).在这一过程中,三角尺起着什么样的
作用?
探索新知
请按下图所示方法画两条平行线,然后讨论下面的问题:
(1)上面的画法可以看做是怎样的图形变换?
(2)把图中的直线l1,l2看成被尺边AB 所截,那么在画图过程中,什么角始终保持相等?
平移变换
同位角
由此你能发现判定两直线平行的方法吗?
探索新知
一般地,判断两直线平行有下面的方法:
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单地说,同位角相等,两直线平行.
探索新知
如图,已知∠1=∠2,则下列结论正确的是( )
A.AD∥BC B.AB ∥ CD
C.AD ∥ EF D.EF ∥ BC
要判定哪两条直线平行,就是要确定∠1,∠2是哪两条直线被第三条直线截得到的同位角, 即找出∠1,∠2除公共边所在直线外的另两边所在直线.
C
导引:
例1
探索新知
在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
垂直总与直角联系在一起,进而用判断两条直线平行的方法进行判定.
例2
分析:
这两条直线平行. 理由如下:
如图.
∵a⊥b,
∴∠1=90°.
同理∠2=90°.
∴∠1=∠2 .
∵ ∠1和∠2 是同位角,
∴b∥c (同位角相等,两直线平行).
答:
探索新知
总 结
判断两条直线是否平行,可以找出这两条直线被第三条直线所截得到的一对同位角,并利用相关角的条件判断其是否相等,如果相等,那么这两条直线平行.
典题精讲
如图,用直尺和三角尺作直线AB,CD,从图中可知,直线AB 与直线CD 的位置关系为________,理由是 .
1
AB∥CD
同位角相等,两直线平行
典题精讲
如图,直线AB,CD 被直线EF 所截,∠1=55°,下列条件中能判定AB∥CD的是( )
A.∠2=35°
B.∠2=45°
C.∠2=55°
D.∠2=125°
2
C
典题精讲
如图,能判定EB∥AC 的条件是( )
A.∠C=∠ABE
B.∠A=∠EBD
C.∠C=∠ABC
D.∠C=∠EBD
3
D
典题精讲
如图,已知∠1=∠2,则下列结论正确的是( )
A.AD ∥ BC
B.AB ∥ CD
C.AD ∥ EF
D.EF ∥ BC
4
C
探索新知
2
知识点
由“第三直线”判定两直线平行
如图,你能说出木工用图中的角尺画平行线的道理吗
探索新知
总 结
平行于同一条直线的两直线平行.
探索新知
如图所示,直线AB、CD 是一条河的两岸,并AB∥CD,点E 为直线AB、CD 外一点.现想过点E 作CD 的平行线,则只需过点E 作岸AB 的平行线即可.其理由是什么
例3
探索新知
利用平行线的性质,把实际问题转化为数学
问题回答.
解:
分析:
理由是(1)过直线外一点有且只有一条直线与
已知直线平行.(2)如果两条直线都与第三条
直线平行,那么这两条直线也互相平行.
探索新知
总 结
在同一平面内和一条直线平行的直线也互相平行.
典题精讲
如图,木工师傅利用直角尺在木板上画出两条线段,则线段AB______CD.
1
∥
典题精讲
在每一步推理后面的括号内填上理由.
(1)如图①,因为AB∥CD,EF∥CD,
所以AB∥EF ( ).
(2)如图②,因为AB∥CD,过点F 作EF∥AB
( ) ,
所以EF∥CD ( ).
2
平行于同一直线的两条直线平行
过直线外一点,有且只有一条直线与这条直线平行
平行于同一直线的两条直线平行
典题精讲
在同一个平面内,不重合的两个直角,如果它们有一条边共线,那么另一条边( )
A.互相平行 B.互相垂直
C.共线 D.互相平行或共线
3
D
易错提醒
如图,已知AB⊥BD 于点B,CD⊥BD 于点D,
∠1=∠2,试问CD 与EF 平行吗?为什么?
解:CD∥EF.理由:因为∠1=∠2(__________),
所以AB∥EF(______________________________).
因为AB⊥BD,CD⊥BD,
所以AB∥CD (____________________ _______ __________).
所以CD∥EF(______________ _____________________).
已知
同位角相等,两直线平行
平行于同一条直线的两条直线互相平行
在同一平面内,垂直于同一条直线的两条直线互相平行
易错点:填错理由而致错.
学以致用
小试牛刀
如图,CD 平分∠ACE,且∠B=∠ACD,可以得出的结论是( )
A.AD∥BC
B.AB ∥ CD
C.CA平分∠BCD
D.AC平分∠BAD
B
1
小试牛刀
三条直线a,b,c,若a∥c,b∥c,则a 与b 的位置关系是( )
A.a⊥b B.a∥b
C.a⊥b或a∥b D.无法确定
2
B
小试牛刀
如图,点B 在DC上,BE 平分∠ABD,
∠ABE=∠C,试说明:BE∥AC.
解:因为BE 平分∠ABD,
所以∠ABE=∠DBE (___________________).
因为∠ABE=∠C,
所以∠DBE=∠C.
所以BE∥AC (__________________________).
角平分线的定义
同位角相等,两直线平行
3
小试牛刀
如图,已知∠1=68°,∠2=68°,∠3=112°.
(1)因为∠1=68°,∠2=68°(已知),
所以∠1=∠2.
所以______ ∥ ______(同位角相等,两直线平行)
(2)因为∠3+∠4=180°(邻补角的定义),∠3=112°,
所以∠4=68°.
又因为∠2=68°,
所以∠2=∠4.
所以______ ∥ ______(同位角相等,两直线平行).
a
b
b
c
4
小试牛刀
如图,已知直线a,b,c,d,e,且∠1=∠2,∠3=
∠4,则a 与c 平行吗?为什么?
解:a 与c 平行.
理由:因为∠1=∠2(__________),
所以a∥b(________________ ________).
因为∠3=∠4(__________________),
所以b∥c (____________ _____________).
所以a∥c (______ __________________________).
已知
同位角相等,两直线平行
已知
同位角相等,两直线平行
平行于同一条直线的两条直线平行
5
小试牛刀
如图,已知∠1=90°,∠2=90°,试说明:CD∥EF.
(1)方法一:用“同位角相等”说明;
(2)方法二:用“第三直线”说明.
(1)方法一:因为∠1=90°,∠2=90°,
所以∠1=∠2.所以CD∥EF.
(2)方法二:因为∠1=90°,∠2=90°,
所以CD⊥AB,EF⊥AB.
所以CD∥EF.
6
小试牛刀
在同一平面内,已知A,B,C 是直线l 同旁的三个点.
(1)若AB∥l,BC∥l,则A,B,C 三点在同一条直线上吗?为什么?
(2)若AB⊥l,BC⊥l,则A,B,C 三点在同一条直线上吗?为什么?
解:
(1)在同一条直线上.理由:因为直线AB,BC 都经过点B,且都与直线l 平行,而过直线外一点有且只有一条直线与这条直线平行,所以AB,BC为同一条直线,所以A,B,C 三点在同一条直线上.
(2)在同一条直线上.理由:因为直线AB,BC 都经过点B,且都与直线l垂直,而在同一平面内,过一点有且只有一条直线与已知直线垂直,所以AB,BC 为同一条直线,所以A,B,C 三点在同一条直线上.
7
课堂小结
课堂小结
判定两直线平行的方法:
(1)利用平行线的定义判定;
(2)利用“同位角相等,两直线平行”判定;
(3)利用“第三直线”判定.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
