【班海精品】人教版(新)七下-5.2 平行线及其判定 第三课时【优质课件】
文档属性
| 名称 | 【班海精品】人教版(新)七下-5.2 平行线及其判定 第三课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 8.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-09 17:35:23 | ||
图片预览










文档简介
(共48张PPT)
5.2 平行线及其判定
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
判断两直线平行的方法:
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单地说,同位角相等,两直线平行.
新课精讲
探索新知
1
知识点
由“内错角相等”判定两直线平行
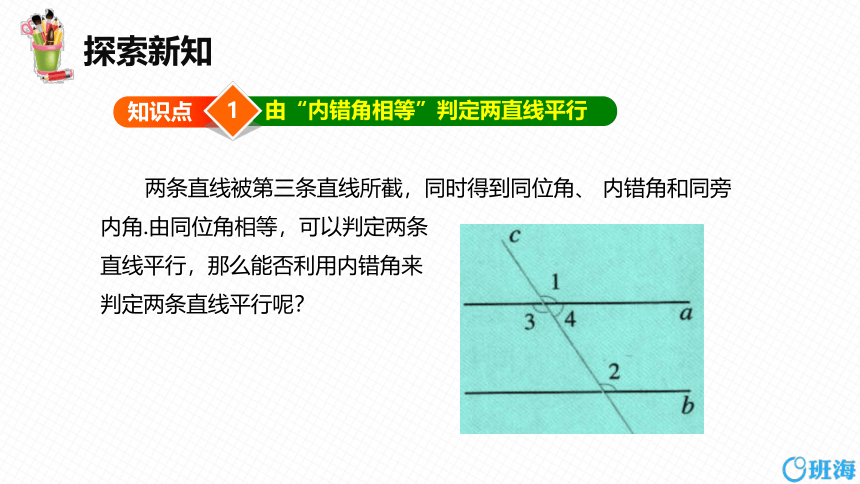
两条直线被第三条直线所截,同时得到同位角、 内错角和同旁内角.由同位角相等,可以判定两条
直线平行,那么能否利用内错角来
判定两条直线平行呢?
探索新知
总 结
判定方法2 两条直线被第三条直线所截,如果内错
角相等,那么这两条 直线平行.
简单说成:内错角相等,两直线平行.
探索新知
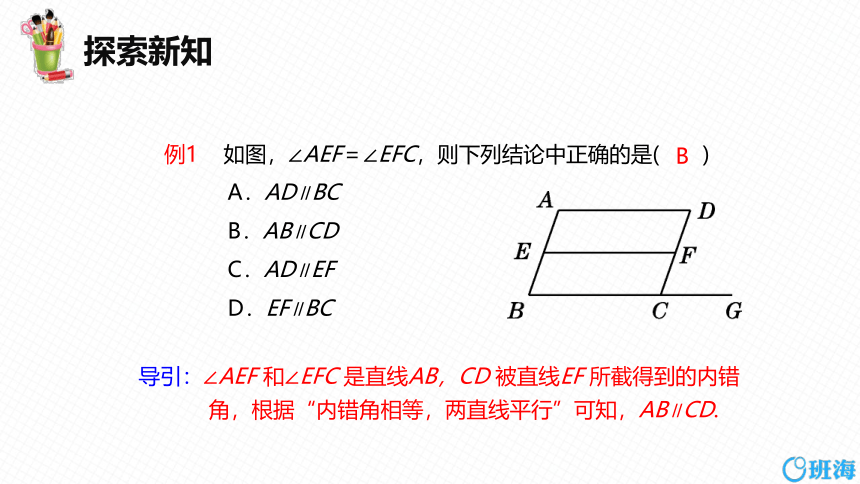
例1 如图,∠AEF=∠EFC,则下列结论中正确的是( )
A.AD∥BC
B.AB∥CD
C.AD∥EF
D.EF∥BC
导引:∠AEF 和∠EFC 是直线AB,CD 被直线EF 所截得到的内错
角,根据“内错角相等,两直线平行”可知,AB∥CD.
B
探索新知
总 结
利用内错角相等来判定两直线平行的方法:
(1)看两角是不是两直线被第三条直线截得的角;
(2)看两角是不是由上述直线形成的内错角,若是,看其是否相等.若相等,则两条直线平行.
探索新知
例2 如图,已知∠ADE=60°,DF 平分∠ADE,∠1=30°,
试说明:DF∥BE.
导引:要想说明DF∥BE,可通过说明∠1=∠EDF
来实现,由于∠1=30°,所以只需求出∠EDF
=30°,而这个结论可通过DF 是∠ADE 的平分
线来求得.
探索新知
解:∵DF 平分∠ADE(已知),
∴∠EDF= ∠ADE (角平分线的定义).
又∵∠ADE=60°,
∴∠EDF=30°.
又∵∠1=30°(已知),
∴∠EDF=∠1,
∴DF∥BE (内错角相等,两直线平行).
探索新知
总 结
要判定两直线平行可以通过说明同位角相等或内错角相等来实现,至于到底选用同位角还是选用内错角,要看具体的题目,要尽可能与已知条件联系.
典题精讲
如图,BE 是AB 的延长线.
(1)由∠CBE= ∠A 可以判定哪两条直线平行? 根据是什么?
(2)由∠CBE= ∠C 可以判定哪两条直线平行? 根据是什么?
1
(1)由∠CBE=∠A可以判定AD∥BC.
根据是:同位角相等,两直线平行.
(2)由∠CBE=∠C可以判定AB∥CD.
根据是:内错角相等,两直线平行.
解:
典题精讲
如图,已知∠1=∠2,则图中互相平行的线段是____________.
2
AD与BC
典题精讲
如图,已知∠1=120°,当∠2=________时,a∥b,理由是 .
3
120°
内错角相等,则两条直线平行
典题精讲
下列图形中,由∠1=∠2能得到AB∥CD 的是( )
4
B
典题精讲
如图,在四边形ABCD 中,连接AC,BD,若要使AB∥CD,则需要添加的条件是( )
A.∠1=∠2
B.∠2=∠3
C.∠3=∠4
D.∠4=∠5
5
D
探索新知
2
知识点
由“同旁内角互补”判定两直线平行
探究
遇到一个新问题时,常常把它转化为已知的(或已
解决的)问题. 这一节中,我们是怎样利用“同位角相
等,两直线平行”得到“内错角相 等,两直线平行”
的?你能利用“同位角相等,两直线平行”或“内错
角相等,两直线平行”得到“同旁内角互补,两直线
平行”吗?
探索新知
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简称:同旁内角互补,两直线平行.
表达方式:如图:
∵∠1+∠2=180°(已知),
∴a∥b (同旁内角互补,两直线平行).
探索新知
例3 如图,直线AE,CD 相交于点O,如果∠A=110°,∠1
=70°,就可以说明AB∥CD,这是为什么?
导引:由题意可知∠1=∠AOD=70°,
又∵∠A=110°,
∴∠A+∠AOD=180°,故 AB∥CD.
探索新知
解:因为∠1=∠AOD (对顶角相等),∠1=70°,
所以∠AOD=70°.
又因为∠A=110°,
所以∠A+∠AOD=180°(等式的性质).
所以AB∥CD (同旁内角互补,两直线平行).
探索新知
总 结
1.本题运用数形结合思想.平行线的判定是由角之间的数量关系到“形”的判定.要判定两直线平行,可围绕截线找同位角、内错角或同旁内角,若同位角相等、内错角相等或同旁内角互补,则两直线平行.
2.用同位角相等、内错角相等或同旁内角互补中的一个方法说明两直线平行时,一般都要通过结合对顶角、邻补角等知识来说明.
探索新知
例4 如图,∠1=65°,∠2=65°,∠3=115°,试
说明(1)DE∥BC; (2)DF∥AB.
根据图形,完成下列推理:
(1)∵∠1=65°,∠2=65°,
∴∠1=∠2.
∴_____∥ ____( ).
(2)∵AB,DE 相交,∴∠1=∠4( ).
∴∠4=65°,又∵∠3=115°,
∴∠3+∠4=180°,
∴____ ∥ ____( ).
DE
BC
同位角相等,两直线平行
对顶角相等
DF
AB
同旁内角互补,两直线平行
探索新知
∠1与∠2是直线DE,BC 被直线AB 所截得到的同位角,所以DE∥BC,理由是“同位角相等,两直线平行”.∠1与∠4是两条直线AB与DE 相交得到的对顶角,所以∠1=∠4,理由是“对顶角相等”,∠3与∠4是直线DF,AB 被直线DE 所截得到的同旁内角,所以DF∥AB,理由是“同旁内角互补,两直线平行”.
导引:
探索新知
总 结
(1)由两角相等或互补关系,判定两条直线平行,其
关键是找出两个角是哪两条直线被哪一条直线所
截而成的角.
(2)是选用两角相等,还是选用互补关系说明两直线
平行,应根据实际图形,灵活运用其中一种方法
说明即可.
探索新知
判定两直线平行的方法:
方法一:平行线的定义:在同一平面内,不相交的两条直线就是平行线.
方法二:如果两条直线都和第三条直线平行,那么这两条直线也互相平行.
方法三:同位角相等,两直线平行.
方法四:内错角相等,两直线平行.
方法五:同旁内角互补,两直线平行.
方法六:在同一平面内,垂直于同一条直线的两条直线平行.
探索新知
例5 如图,直线MN 和直线AB,CD,EF 分别交于点G,H,P,
∠1=∠2,∠2+∠3=180°,试问:AB与EF 平行吗?为什么?
导引:要说明AB∥EF,我们无法找出这两条直线被
MN 所截的角相等或互补的条件,因此可考
虑这两条直线是否同时与第三条直线CD 平行;
即只需说明AB∥CD,EF∥CD 即可.
探索新知
平行.
因为∠1=∠2,∠1=∠BGH,
所以∠2=∠BGH (等量代换),
所以AB∥CD (同位角相等,两直线平行).
所以∠2+∠3=180°,∠3=∠HPF,
所以∠2+∠HPF =180°(等量代换).
所以CD∥EF (同旁内角互补,两直线平行).
所以AB∥EF (如果两条直线都和第三条直线平行,
那么这两条直线也互相平行).
解:
探索新知
总 结
在判定两条直线互相平行的问题中,如果不能直接根据平行线的判定方法得出结论,可根据题目中的已知条件与哪些判定方法的条件相同或相关联,运用转化思想(用第三条直线作中介)将问题进行转化(同平行于第三条直线或同垂直于第三条直线),
使之满足平行线的判定方法.
典题精讲
在铺设铁轨时,两条直轨必须是互相平行的.如图, 已经知道∠2是直角,那么再度量图中已标出的哪个 角,就可以判断两
条直轨是否平行?为什么?
1
再度量题图中的∠3或∠4或
∠5,就可以判断两条直轨
是否平行.理由是:如果再度量∠3或∠4或∠5,就可以分别根据同旁内角是否互补,同位角是否相等,内错角是否相等来判断两条直轨是否平行.
解:
典题精讲
如图,这是小明同学自己制作的英语抄写纸的一部分. 其中的横格线互相平行吗?你有多少种判别方法?
2
其中的横格线互相平行.有4种判别方法:
①同位角相等,两直线平行.
②内错角相等,两直线平行.
③同旁内角互补,两直线平行.
④在同一平面内,如果两条直线都平行于同一条直线,那么这两条直线平行.
解:
典题精讲
如图,工人师傅在工程施工中需在同一平面内弯制一个变形管道ABCD,使其拐角∠ABC=150°,∠BCD=30°,则( )
A.AB∥BC
B.BC∥CD
C.AB∥DC
D.AB与CD 相交
3
C
典题精讲
如图,直线a,b 被直线c 所截,下列条件不能判定直线a与b 平行的是( )
A.∠1=∠3
B.∠2+∠4=180°
C.∠1=∠4
D.∠3=∠4
4
D
典题精讲
如图,直线a 与直线b 交于点A,与直线c 交于点B,∠1=120°,∠2=45°,若使直线b 与直线c 平行,则可将直线b 绕点A 逆时针旋转( )
A.15°
B.30°
C.45°
D.60°
5
A
易错提醒
如图,下列推理正确的有( )
①因为∠1=∠4,所以BC∥AD;
②因为∠2=∠3,所以AB∥CD;
③因为∠BCD+∠ADC=180°,所以AD∥BC;
④因为∠1+∠2+∠C=180°,所以BC∥AD.
A.1个 B.2个 C.3个 D.4个
A
易错点:不能准确识别截线和被截线,从而误判两直线平行.
学以致用
小试牛刀
如图,若∠1与∠2互补,∠2与∠4互补,则( ).
A.L4∥l5
B.l1∥l2
C.l1∥l3
D.l2∥l3
1
C
小试牛刀
如图,点E 在BC 的延长线上,下列条件中能判定BC∥AD 的是( )
A.∠1=∠2 B.∠DAB+∠D=180°
C.∠3=∠4 D.∠B=∠DCE
2
C
小试牛刀
已知:如图,AB⊥BC,CD⊥BC,∠1
=∠2,BE 与CF 平行吗?请说明理由.
补全下面的说理过程,并在括号内填上适当的理由.
解:BE∥CF.理由如下:
∵AB⊥BC,CD⊥BC (___________),
∴∠ABC=∠BCD=________°(垂直的定义).
∵∠1=∠2(_____________),
∴∠EBC=∠FCB (______________________).
∴BE∥CF (____________________________).
已知
90
已知
等角的余角相等
内错角相等,两直线平行
3
小试牛刀
将下面的说明过程补充完整.
已知:如图,直线NF 与直线AB,CD 分别交于点E,F,
直线AM 与直线HB 交于点A,且∠1=∠4=105°,∠2=75°.
试说明:AM∥NF,AB∥CD.
解:∵∠2=∠3(____________),
∠2=75°(已知),∴∠3=75°.
∵∠1=105°(已知),∴∠MAB=180°-∠1=75°.
∴∠MAB=∠3.∴AM∥NF (_______________ _________).
∵∠3=75°,∠4=105°,∴∠3+∠4=180°.
∴AB∥CD(_____________________________).
对顶角相等
同旁内角互补,两直线平行
内错角相等,两直线平行
4
小试牛刀
如图,已知直线a,b,c,d,e,且∠1=∠2,∠3+∠4=180°,
则a 与c 平行吗?为什么?
解:a 与c 平行.
理由:因为∠1=∠2(________),
所以a∥b (____________ ____________).
因为∠3+∠4=180°(__________),
所以b∥c (______ ____________________).
所以a∥c (_________________________ __________
___ ________________________).
已知
内错角相等,两直线平行
已知
同旁内角互补,两直线平行
如果两条直线都与第三条直线平行,
那么这两条直线也互相平行
5
小试牛刀
如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.
解:
OA∥BC,OB∥AC.理由如下:
∵∠1=50°,∠2=50°,
∴∠1=∠2.
∴OB∥AC.
∵∠2=50°,∠3=130°,
∴∠2+∠3=180°.
∴OA∥BC.
6
小试牛刀
如图所示,当∠BED 与∠B,∠D满足条件_________
时,可以判定AB∥CD.
(1)在横线处填上一个条件;
(2)试说明你填写的条件的正确性.
解:
(1)∠BED=∠B+∠D
(2)如图所示,过点E 在∠BED 的内部
作∠BEF=∠B,则AB∥EF.
又因为∠BED=∠B+∠D,所以∠FED=∠D,
所以EF∥CD,所以AB∥CD.
7
小试牛刀
如图,已知∠1=68°,∠2=68°,∠3=112°.
(1)因为∠1=68°,∠2=68°(已知),
所以∠1=∠2.
所以______ ∥ ______(同位角相等,两直线平行)
(2)因为∠3+∠4=180°(邻补角的定义),∠3=112°,
所以∠4=68°.
又因为∠2=68°,
所以∠2=∠4.
所以______ ∥ ______(同位角相等,两直线平行).
a
b
b
c
4
小试牛刀
如图,已知∠1=90°,∠2=90°,试说明:CD∥EF.
(1)方法一:用“同位角相等”说明;
(2)方法二:用“第三直线”说明.
(1)方法一:因为∠1=90°,∠2=90°,
所以∠1=∠2.所以CD∥EF.
(2)方法二:因为∠1=90°,∠2=90°,
所以CD⊥AB,EF⊥AB.
所以CD∥EF.
6
课堂小结
课堂小结
判定两直线平行的方法:
(1)利用平行线的定义判定;
(2)利用“同位角相等,两直线平行”判定;
(3)利用“第三直线”判定.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
5.2 平行线及其判定
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
判断两直线平行的方法:
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单地说,同位角相等,两直线平行.
新课精讲
探索新知
1
知识点
由“内错角相等”判定两直线平行
两条直线被第三条直线所截,同时得到同位角、 内错角和同旁内角.由同位角相等,可以判定两条
直线平行,那么能否利用内错角来
判定两条直线平行呢?
探索新知
总 结
判定方法2 两条直线被第三条直线所截,如果内错
角相等,那么这两条 直线平行.
简单说成:内错角相等,两直线平行.
探索新知
例1 如图,∠AEF=∠EFC,则下列结论中正确的是( )
A.AD∥BC
B.AB∥CD
C.AD∥EF
D.EF∥BC
导引:∠AEF 和∠EFC 是直线AB,CD 被直线EF 所截得到的内错
角,根据“内错角相等,两直线平行”可知,AB∥CD.
B
探索新知
总 结
利用内错角相等来判定两直线平行的方法:
(1)看两角是不是两直线被第三条直线截得的角;
(2)看两角是不是由上述直线形成的内错角,若是,看其是否相等.若相等,则两条直线平行.
探索新知
例2 如图,已知∠ADE=60°,DF 平分∠ADE,∠1=30°,
试说明:DF∥BE.
导引:要想说明DF∥BE,可通过说明∠1=∠EDF
来实现,由于∠1=30°,所以只需求出∠EDF
=30°,而这个结论可通过DF 是∠ADE 的平分
线来求得.
探索新知
解:∵DF 平分∠ADE(已知),
∴∠EDF= ∠ADE (角平分线的定义).
又∵∠ADE=60°,
∴∠EDF=30°.
又∵∠1=30°(已知),
∴∠EDF=∠1,
∴DF∥BE (内错角相等,两直线平行).
探索新知
总 结
要判定两直线平行可以通过说明同位角相等或内错角相等来实现,至于到底选用同位角还是选用内错角,要看具体的题目,要尽可能与已知条件联系.
典题精讲
如图,BE 是AB 的延长线.
(1)由∠CBE= ∠A 可以判定哪两条直线平行? 根据是什么?
(2)由∠CBE= ∠C 可以判定哪两条直线平行? 根据是什么?
1
(1)由∠CBE=∠A可以判定AD∥BC.
根据是:同位角相等,两直线平行.
(2)由∠CBE=∠C可以判定AB∥CD.
根据是:内错角相等,两直线平行.
解:
典题精讲
如图,已知∠1=∠2,则图中互相平行的线段是____________.
2
AD与BC
典题精讲
如图,已知∠1=120°,当∠2=________时,a∥b,理由是 .
3
120°
内错角相等,则两条直线平行
典题精讲
下列图形中,由∠1=∠2能得到AB∥CD 的是( )
4
B
典题精讲
如图,在四边形ABCD 中,连接AC,BD,若要使AB∥CD,则需要添加的条件是( )
A.∠1=∠2
B.∠2=∠3
C.∠3=∠4
D.∠4=∠5
5
D
探索新知
2
知识点
由“同旁内角互补”判定两直线平行
探究
遇到一个新问题时,常常把它转化为已知的(或已
解决的)问题. 这一节中,我们是怎样利用“同位角相
等,两直线平行”得到“内错角相 等,两直线平行”
的?你能利用“同位角相等,两直线平行”或“内错
角相等,两直线平行”得到“同旁内角互补,两直线
平行”吗?
探索新知
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简称:同旁内角互补,两直线平行.
表达方式:如图:
∵∠1+∠2=180°(已知),
∴a∥b (同旁内角互补,两直线平行).
探索新知
例3 如图,直线AE,CD 相交于点O,如果∠A=110°,∠1
=70°,就可以说明AB∥CD,这是为什么?
导引:由题意可知∠1=∠AOD=70°,
又∵∠A=110°,
∴∠A+∠AOD=180°,故 AB∥CD.
探索新知
解:因为∠1=∠AOD (对顶角相等),∠1=70°,
所以∠AOD=70°.
又因为∠A=110°,
所以∠A+∠AOD=180°(等式的性质).
所以AB∥CD (同旁内角互补,两直线平行).
探索新知
总 结
1.本题运用数形结合思想.平行线的判定是由角之间的数量关系到“形”的判定.要判定两直线平行,可围绕截线找同位角、内错角或同旁内角,若同位角相等、内错角相等或同旁内角互补,则两直线平行.
2.用同位角相等、内错角相等或同旁内角互补中的一个方法说明两直线平行时,一般都要通过结合对顶角、邻补角等知识来说明.
探索新知
例4 如图,∠1=65°,∠2=65°,∠3=115°,试
说明(1)DE∥BC; (2)DF∥AB.
根据图形,完成下列推理:
(1)∵∠1=65°,∠2=65°,
∴∠1=∠2.
∴_____∥ ____( ).
(2)∵AB,DE 相交,∴∠1=∠4( ).
∴∠4=65°,又∵∠3=115°,
∴∠3+∠4=180°,
∴____ ∥ ____( ).
DE
BC
同位角相等,两直线平行
对顶角相等
DF
AB
同旁内角互补,两直线平行
探索新知
∠1与∠2是直线DE,BC 被直线AB 所截得到的同位角,所以DE∥BC,理由是“同位角相等,两直线平行”.∠1与∠4是两条直线AB与DE 相交得到的对顶角,所以∠1=∠4,理由是“对顶角相等”,∠3与∠4是直线DF,AB 被直线DE 所截得到的同旁内角,所以DF∥AB,理由是“同旁内角互补,两直线平行”.
导引:
探索新知
总 结
(1)由两角相等或互补关系,判定两条直线平行,其
关键是找出两个角是哪两条直线被哪一条直线所
截而成的角.
(2)是选用两角相等,还是选用互补关系说明两直线
平行,应根据实际图形,灵活运用其中一种方法
说明即可.
探索新知
判定两直线平行的方法:
方法一:平行线的定义:在同一平面内,不相交的两条直线就是平行线.
方法二:如果两条直线都和第三条直线平行,那么这两条直线也互相平行.
方法三:同位角相等,两直线平行.
方法四:内错角相等,两直线平行.
方法五:同旁内角互补,两直线平行.
方法六:在同一平面内,垂直于同一条直线的两条直线平行.
探索新知
例5 如图,直线MN 和直线AB,CD,EF 分别交于点G,H,P,
∠1=∠2,∠2+∠3=180°,试问:AB与EF 平行吗?为什么?
导引:要说明AB∥EF,我们无法找出这两条直线被
MN 所截的角相等或互补的条件,因此可考
虑这两条直线是否同时与第三条直线CD 平行;
即只需说明AB∥CD,EF∥CD 即可.
探索新知
平行.
因为∠1=∠2,∠1=∠BGH,
所以∠2=∠BGH (等量代换),
所以AB∥CD (同位角相等,两直线平行).
所以∠2+∠3=180°,∠3=∠HPF,
所以∠2+∠HPF =180°(等量代换).
所以CD∥EF (同旁内角互补,两直线平行).
所以AB∥EF (如果两条直线都和第三条直线平行,
那么这两条直线也互相平行).
解:
探索新知
总 结
在判定两条直线互相平行的问题中,如果不能直接根据平行线的判定方法得出结论,可根据题目中的已知条件与哪些判定方法的条件相同或相关联,运用转化思想(用第三条直线作中介)将问题进行转化(同平行于第三条直线或同垂直于第三条直线),
使之满足平行线的判定方法.
典题精讲
在铺设铁轨时,两条直轨必须是互相平行的.如图, 已经知道∠2是直角,那么再度量图中已标出的哪个 角,就可以判断两
条直轨是否平行?为什么?
1
再度量题图中的∠3或∠4或
∠5,就可以判断两条直轨
是否平行.理由是:如果再度量∠3或∠4或∠5,就可以分别根据同旁内角是否互补,同位角是否相等,内错角是否相等来判断两条直轨是否平行.
解:
典题精讲
如图,这是小明同学自己制作的英语抄写纸的一部分. 其中的横格线互相平行吗?你有多少种判别方法?
2
其中的横格线互相平行.有4种判别方法:
①同位角相等,两直线平行.
②内错角相等,两直线平行.
③同旁内角互补,两直线平行.
④在同一平面内,如果两条直线都平行于同一条直线,那么这两条直线平行.
解:
典题精讲
如图,工人师傅在工程施工中需在同一平面内弯制一个变形管道ABCD,使其拐角∠ABC=150°,∠BCD=30°,则( )
A.AB∥BC
B.BC∥CD
C.AB∥DC
D.AB与CD 相交
3
C
典题精讲
如图,直线a,b 被直线c 所截,下列条件不能判定直线a与b 平行的是( )
A.∠1=∠3
B.∠2+∠4=180°
C.∠1=∠4
D.∠3=∠4
4
D
典题精讲
如图,直线a 与直线b 交于点A,与直线c 交于点B,∠1=120°,∠2=45°,若使直线b 与直线c 平行,则可将直线b 绕点A 逆时针旋转( )
A.15°
B.30°
C.45°
D.60°
5
A
易错提醒
如图,下列推理正确的有( )
①因为∠1=∠4,所以BC∥AD;
②因为∠2=∠3,所以AB∥CD;
③因为∠BCD+∠ADC=180°,所以AD∥BC;
④因为∠1+∠2+∠C=180°,所以BC∥AD.
A.1个 B.2个 C.3个 D.4个
A
易错点:不能准确识别截线和被截线,从而误判两直线平行.
学以致用
小试牛刀
如图,若∠1与∠2互补,∠2与∠4互补,则( ).
A.L4∥l5
B.l1∥l2
C.l1∥l3
D.l2∥l3
1
C
小试牛刀
如图,点E 在BC 的延长线上,下列条件中能判定BC∥AD 的是( )
A.∠1=∠2 B.∠DAB+∠D=180°
C.∠3=∠4 D.∠B=∠DCE
2
C
小试牛刀
已知:如图,AB⊥BC,CD⊥BC,∠1
=∠2,BE 与CF 平行吗?请说明理由.
补全下面的说理过程,并在括号内填上适当的理由.
解:BE∥CF.理由如下:
∵AB⊥BC,CD⊥BC (___________),
∴∠ABC=∠BCD=________°(垂直的定义).
∵∠1=∠2(_____________),
∴∠EBC=∠FCB (______________________).
∴BE∥CF (____________________________).
已知
90
已知
等角的余角相等
内错角相等,两直线平行
3
小试牛刀
将下面的说明过程补充完整.
已知:如图,直线NF 与直线AB,CD 分别交于点E,F,
直线AM 与直线HB 交于点A,且∠1=∠4=105°,∠2=75°.
试说明:AM∥NF,AB∥CD.
解:∵∠2=∠3(____________),
∠2=75°(已知),∴∠3=75°.
∵∠1=105°(已知),∴∠MAB=180°-∠1=75°.
∴∠MAB=∠3.∴AM∥NF (_______________ _________).
∵∠3=75°,∠4=105°,∴∠3+∠4=180°.
∴AB∥CD(_____________________________).
对顶角相等
同旁内角互补,两直线平行
内错角相等,两直线平行
4
小试牛刀
如图,已知直线a,b,c,d,e,且∠1=∠2,∠3+∠4=180°,
则a 与c 平行吗?为什么?
解:a 与c 平行.
理由:因为∠1=∠2(________),
所以a∥b (____________ ____________).
因为∠3+∠4=180°(__________),
所以b∥c (______ ____________________).
所以a∥c (_________________________ __________
___ ________________________).
已知
内错角相等,两直线平行
已知
同旁内角互补,两直线平行
如果两条直线都与第三条直线平行,
那么这两条直线也互相平行
5
小试牛刀
如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.
解:
OA∥BC,OB∥AC.理由如下:
∵∠1=50°,∠2=50°,
∴∠1=∠2.
∴OB∥AC.
∵∠2=50°,∠3=130°,
∴∠2+∠3=180°.
∴OA∥BC.
6
小试牛刀
如图所示,当∠BED 与∠B,∠D满足条件_________
时,可以判定AB∥CD.
(1)在横线处填上一个条件;
(2)试说明你填写的条件的正确性.
解:
(1)∠BED=∠B+∠D
(2)如图所示,过点E 在∠BED 的内部
作∠BEF=∠B,则AB∥EF.
又因为∠BED=∠B+∠D,所以∠FED=∠D,
所以EF∥CD,所以AB∥CD.
7
小试牛刀
如图,已知∠1=68°,∠2=68°,∠3=112°.
(1)因为∠1=68°,∠2=68°(已知),
所以∠1=∠2.
所以______ ∥ ______(同位角相等,两直线平行)
(2)因为∠3+∠4=180°(邻补角的定义),∠3=112°,
所以∠4=68°.
又因为∠2=68°,
所以∠2=∠4.
所以______ ∥ ______(同位角相等,两直线平行).
a
b
b
c
4
小试牛刀
如图,已知∠1=90°,∠2=90°,试说明:CD∥EF.
(1)方法一:用“同位角相等”说明;
(2)方法二:用“第三直线”说明.
(1)方法一:因为∠1=90°,∠2=90°,
所以∠1=∠2.所以CD∥EF.
(2)方法二:因为∠1=90°,∠2=90°,
所以CD⊥AB,EF⊥AB.
所以CD∥EF.
6
课堂小结
课堂小结
判定两直线平行的方法:
(1)利用平行线的定义判定;
(2)利用“同位角相等,两直线平行”判定;
(3)利用“第三直线”判定.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
