【班海精品】人教版(新)七下-5.3 平行线的性质 第一课时【优质课件】
文档属性
| 名称 | 【班海精品】人教版(新)七下-5.3 平行线的性质 第一课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 8.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-09 17:35:23 | ||
图片预览








文档简介
(共51张PPT)
5.3 平行线的性质
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
复
习
回
顾
条件
结论
平行线的判定
同位角相等
内错角相等
同旁内角互补
两直线平行
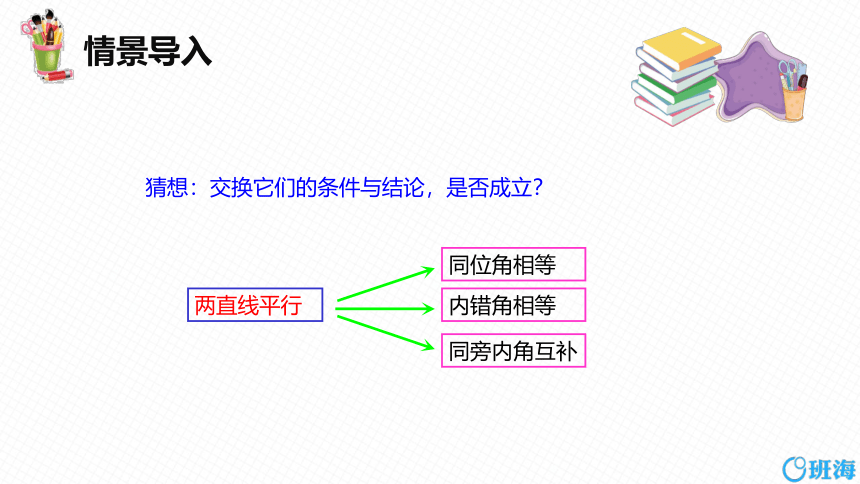
情景导入
两直线平行
同位角相等
内错角相等
同旁内角互补
猜想:交换它们的条件与结论,是否成立?
新课精讲
探索新知
1
知识点
“同位角”的性质
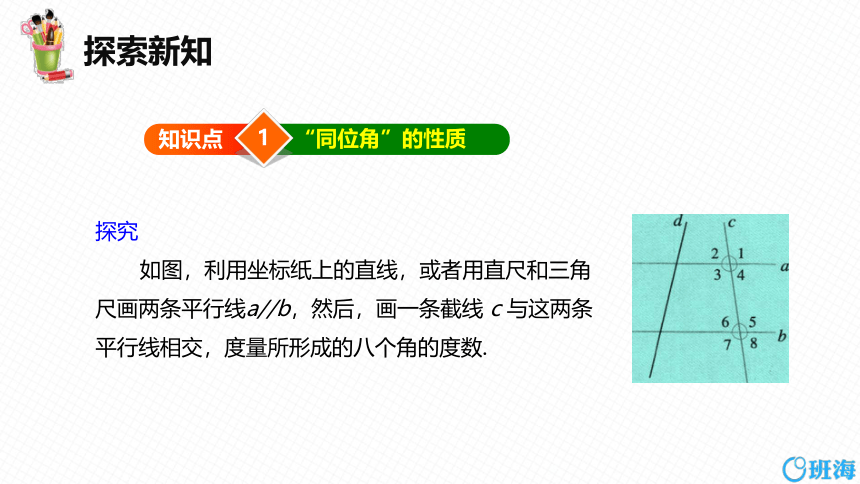
探究
如图,利用坐标纸上的直线,或者用直尺和三角
尺画两条平行线a//b,然后,画一条截线 c 与这两条
平行线相交,度量所形成的八个角的度数.
探索新知
两条平行线被第三条直线截得的同位角会具有怎样的数量关系?
性质1 两条平行线被第三条直线所截,同位角相等.
探索新知
A
B
P
C
D
E
F
2
1
探索新知
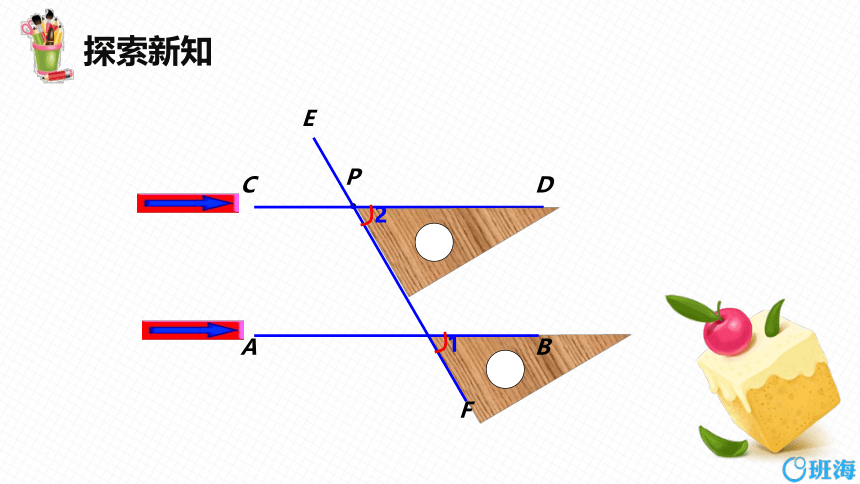
表达方式:如图,∵a∥b (已知),
∴∠1=∠2(两直线平行,同位角相等).
探索新知
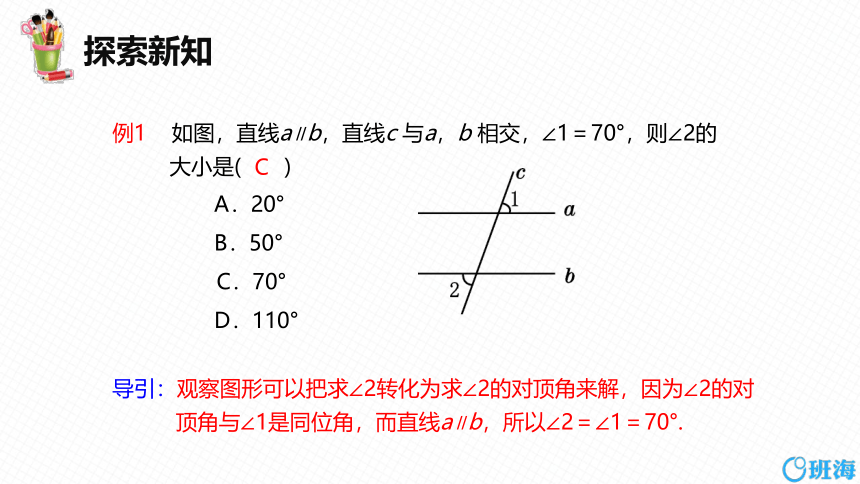
例1 如图,直线a∥b,直线c 与a,b 相交,∠1=70°,则∠2的
大小是( )
A.20°
B.50°
C.70°
D.110°
导引:观察图形可以把求∠2转化为求∠2的对顶角来解,因为∠2的对
顶角与∠1是同位角,而直线a∥b,所以∠2=∠1=70°.
C
探索新知
总 结
有关两直线平行,同位角相等的性质,分清两
个角的位置关系是解答此类题目的关键.
探索新知
例2 如图,若AB∥CD,且∠1=∠2,试判断AM 与CN 的位置关系,
并说明理由.
导引:AM 与CN 的位置关系很显然是平行,
要说明AM∥CN,可考虑说明∠EAM=
∠ECN. 因为∠1=∠2,所以只需说明
∠BAE=∠ACD 即可,由于“两直线平行,
同位角相等”,所以根据 AB∥CD,即可
得出∠BAE=∠ACD.
探索新知
解:AM∥CN.
理由:∵AB∥CD (已知),
∴∠BAE=∠ACD (两直线平行,同位角相等).
又∵∠1=∠2(已知),
∴∠EAM=∠ECN (等式性质).
∴AM∥CN (同位角相等,两直线平行).
探索新知
总 结
平行线和角的大小关系是紧密联系在一起的,
由平行线可以得到相等的角,反过来又可以由相等
的角得到新的一组平行线,这种角的大小关系与直
线的位置关系的相互转化在解题中会经常涉及.当
题目已知条件中出现两直线平行时,要考虑是否出
现了相等的角.
典题精讲
1
如图,直线a∥b,∠1= 54°, ∠ 2,∠ 3,∠4各是多少度?
∠2=∠1=54°(对顶角相等).
因为a∥b,∠1=54°,
所以∠4=∠1=54°(两直线平行,同位角相等),
所以∠3=180°-∠4=126°(邻补角定义).
解:
典题精讲
2
如图,三角形ABC 中,D 是AB上一点,E 是AC上一点,∠ADE = 60°, ∠B=60°,∠AED=60°.
(1)DE 和BC 平行吗?为什么?
(2)∠C 是多少度?为什么?
(1)DE 和BC 平行.因为∠ADE=∠B=60°,所以DE∥BC (同位角相等,两直线平行).
(2)∠C=40°.因为DE∥BC,所以∠C=∠AED=40°(两直线平行,同位角相等).
解:
A
C
典题精讲
3
如图,直线a,b 被直线c 所截,若直线a∥b,∠1=108°,则∠2的度数为( )
A.108°
B.82°
C.72°
D.62°
C
典题精讲
4
如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=50°,则∠2的度数为( ).
A.50°
B.40°
C.30°
D.25°
B
典题精讲
5
如图,AB∥DE,FG⊥BC 于F,∠CDE=40°,则∠FGB= ( )
A.40°
B.50°
C.60°
D.70°
B
典题精讲
6
如图,直线a∥b,∠1=60°,∠2=40°,则∠3等于( )
A.40°
B.60°
C.80°
D.100°
C
探索新知
2
知识点
“内错角”的性质
性质2 两条平行线被第三条直线所截,内错角相等.
两条平行线被第三条直线截得的内错角会具有怎样的数量关系?
探索新知
表达方式:如图因为a∥b(已知),
所以∠1=∠2(两直线平行,内错角相等).
探索新知
例3 如图,MN,EF 表示两面互相平行的镜面,一
束光线AB 照射到镜面MN上,反射光线为BC,
此时∠1=∠2,光线BC 经过镜面EF 反射后的
光线为CD,此时∠3=∠4,试判断AB 与CD 的
位置关系,并说明理由.
探索新知
导引:要判断AB与CD的位置关系,应从两直线的位置关系的
特殊情况,如平行或垂直方面思考问题,观察图可知,
AB与CD 没有交点,所以可猜想AB∥CD,要说明
AB∥CD,只要说明∠ABC=∠BCD 即可.
探索新知
解:AB∥CD,理由如下:
∵MN∥EF,
∴∠2=∠3(两直线平行,内错角相等).
∵∠1=∠2,∠2=∠3,∠3=∠4,
∴∠1+∠2=∠3+∠4.
∵∠1+∠ABC+∠2=180°,
∠3+∠BCD+∠4=180°,
∴∠ABC=∠BCD.
∴AB∥CD(内错角相等,两直线平行).
探索新知
总 结
(1)利用平行线的性质解决实际问题时,其关键是根
据实际问题建立数学模型;
(2)判断两直线的位置关系时,一般都从两直线平行
或垂直这两种特殊情况去思考.
典题精讲
1
如图,已知a∥b,小华把三角板的直角顶点放在直线b上.若∠1=40°,则∠2的度数为( ).
A.100°
B.110°
C.120°
D.130°
D
典题精讲
2
已知直线m∥n,将一块含30°角的直角三角尺ABC 按如图方式放置(∠ABC=30°),其中A,B 两点分别落在m,n上,若∠1=20°,则∠2的度数为( )
A.20°
B.30°
C.45°
D.50°
D
探索新知
3
知识点
“同旁内角”的性质
“同旁内角”的性质:
性质3 两条平行线被第三条直线所截,同旁内角互补.
探索新知
表达方式:如图,因为a∥b(已知),
所以∠1+∠2=180°(两直线平行,同旁内角互补).
探索新知
例4 如图,如果AB∥DF,DE∥BC,且∠1=65°,那么你能说出∠2,∠3,∠4的度数吗?为什么?
导引:由DE∥BC,可得∠1=∠4,∠1+∠2=180°;由DF∥AB,可得∠3=∠2,从而得∠2,∠3,∠4的度数.
探索新知
解:∵DE∥BC (已知),
∴∠4=∠1=65°(两直线平行,内错角相等),
∠2+∠1=180°(两直线平行,同旁内角互补).
∴∠2=180°-∠1=180°-65°=115°.
又∵DF∥AB (已知),
∴∠3=∠2(两直线平行,同位角相等).
∴∠3=115°(等量代换).
探索新知
总 结
1.求角的度数的基本思路:根据平行线的判定由角的数量
关系得到直线的位置关系,根据平行线的性质由直线的
位置关系得到角的数量关系,通过上述相互转化,从而
找到所求角与已知角之间的关系.
2.两直线平行时,应联想到平行线的三个性质,由两条直
线平行的位置关系得到两个相关角的数量关系,由角的
关系求相应角的度数.
典题精讲
1
如图所示,要在一条公路的两侧铺设平行管道,已知一侧铺设的角度为120°,为使管道对接,另一侧铺设的角度大小应为( )
A.120°
B.100°
C.80°
D.60°
D
典题精讲
2
如图,已知a∥b,直角三角尺的直角顶点在直线b上,若∠1=60°,则下列结论错误的是( )
A.∠2=60°
B.∠3=60°
C.∠4=120°
D.∠5=40°
D
易错提醒
已知∠1与∠2是同旁内角.若∠1=50°,则∠2的度数是( )
A.50° B.130°
C.50°或130° D.不能确定
D
易错点:利用平行线的性质时易忽视两直线平行这
一前提而出错.
学以致用
小试牛刀
如图,已知a∥b,∠1=50°,∠2=90°,则∠3的度数为( )
A.40°
B.50°
C.150°
D.140°
D
1
小试牛刀
如图,已知AB∥CD∥EF,FC 平分∠AFE,∠C=25°,则∠A的度数是( )
A.25°
B.35°
C.45°
D.50°
D
2
小试牛刀
如图,AB∥CD,点E 是CD上一点,∠AEC=42°,EF 平分∠AED 交AB 于点F,求∠AFE 的度数.
解:
∵∠AEC=42°,∠AEC+∠AED=180°,
∴∠AED=180°-∠AEC=138°.
∵EF 平分∠AED,
∴∠DEF= ∠AED=69°.
又∵AB∥CD,∴∠AFE=∠DEF=69°.
3
小试牛刀
如图,已知AD⊥BC 于D,EG⊥BC 于G,∠E=∠3.
AD 是∠BAC 的平分线吗?若是,请说明理由.
解:
AD 是∠BAC 的平分线.理由如下:
∵AD⊥BC,EG⊥BC,∴EG∥AD.
∴∠3=∠1,∠E=∠2.
又∵∠E=∠3,
∴∠1=∠2,
即AD 是∠BAC 的平分线.
4
小试牛刀
如图:已知AB∥CD,EF⊥AB 于点O,∠FGC=125°,
求∠EFG 的度数.
下面提供三种思路:
(1)过点F 作FH∥AB;
(2)延长EF 交CD 于M;
(3)延长GF 交AB 于K.
请你利用三个思路中的两个思路,将图形补充完整,
求∠EFG 的度数.
小试牛刀
解:
(一)利用思路(1).
过点F 作FH∥AB,如图①.
∵EF⊥AB,∴∠BOF=90°,
∵FH∥AB,∴∠HFO=∠BOF=90°,
∵AB∥CD,∴FH∥CD,∴∠FGC+∠GFH=180°,
∵∠FGC=125°,∴∠GFH=55°,
∴∠EFG=∠GFH+∠HFO=55°+90°=145°;
小试牛刀
(二)利用思路(2).延长EF 交CD 于点M,如图②.
∵EF⊥AB,∴∠BOF=90°,
∵CD∥AB,∴∠CMF=∠BOF=90°,
∵∠FGC=125°,∴∠1=55°,
∵∠1+∠2+∠GMF=180°,
∴∠2=35°,∵∠GFO+∠2=180°,
∴∠GFO=145°,即∠EFG=145°.
小试牛刀
直线AB∥CD,点P 是直线AB,CD 外的任意一点,连接PA,PC.
(1)探究猜想:
①如图①,若∠A=30°,∠C=40°,则∠APC=________°;
②如图①,若∠A=40°,∠C=60°,则∠APC =________°;
70
100
小试牛刀
解:
③∠APC=∠A+∠C.理由如下:
过P 点向左侧作PE∥AB,则∠APE=∠A,
∵AB∥CD,∴PE∥CD,
∴∠CPE=∠C.
又∵∠APC=∠APE+∠CPE,
∴∠APC=∠A+∠C.
③猜想图①中∠A,∠C,∠APC 三者之间有怎样的等量关系?并说明理由.
小试牛刀
(2)拓展:
①如图②,若∠A=20°,∠C=50°,则∠APC=________°;
②猜想图③中∠A,∠C,∠APC 三者之间的关系为____________________.
30
∠APC=∠A-∠C
课堂小结
课堂小结
平行线的三个性质:
两直线平行,同位角相等.
两直线平行,内错角相等.
两直线平行,同旁内角互补.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
5.3 平行线的性质
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
复
习
回
顾
条件
结论
平行线的判定
同位角相等
内错角相等
同旁内角互补
两直线平行
情景导入
两直线平行
同位角相等
内错角相等
同旁内角互补
猜想:交换它们的条件与结论,是否成立?
新课精讲
探索新知
1
知识点
“同位角”的性质
探究
如图,利用坐标纸上的直线,或者用直尺和三角
尺画两条平行线a//b,然后,画一条截线 c 与这两条
平行线相交,度量所形成的八个角的度数.
探索新知
两条平行线被第三条直线截得的同位角会具有怎样的数量关系?
性质1 两条平行线被第三条直线所截,同位角相等.
探索新知
A
B
P
C
D
E
F
2
1
探索新知
表达方式:如图,∵a∥b (已知),
∴∠1=∠2(两直线平行,同位角相等).
探索新知
例1 如图,直线a∥b,直线c 与a,b 相交,∠1=70°,则∠2的
大小是( )
A.20°
B.50°
C.70°
D.110°
导引:观察图形可以把求∠2转化为求∠2的对顶角来解,因为∠2的对
顶角与∠1是同位角,而直线a∥b,所以∠2=∠1=70°.
C
探索新知
总 结
有关两直线平行,同位角相等的性质,分清两
个角的位置关系是解答此类题目的关键.
探索新知
例2 如图,若AB∥CD,且∠1=∠2,试判断AM 与CN 的位置关系,
并说明理由.
导引:AM 与CN 的位置关系很显然是平行,
要说明AM∥CN,可考虑说明∠EAM=
∠ECN. 因为∠1=∠2,所以只需说明
∠BAE=∠ACD 即可,由于“两直线平行,
同位角相等”,所以根据 AB∥CD,即可
得出∠BAE=∠ACD.
探索新知
解:AM∥CN.
理由:∵AB∥CD (已知),
∴∠BAE=∠ACD (两直线平行,同位角相等).
又∵∠1=∠2(已知),
∴∠EAM=∠ECN (等式性质).
∴AM∥CN (同位角相等,两直线平行).
探索新知
总 结
平行线和角的大小关系是紧密联系在一起的,
由平行线可以得到相等的角,反过来又可以由相等
的角得到新的一组平行线,这种角的大小关系与直
线的位置关系的相互转化在解题中会经常涉及.当
题目已知条件中出现两直线平行时,要考虑是否出
现了相等的角.
典题精讲
1
如图,直线a∥b,∠1= 54°, ∠ 2,∠ 3,∠4各是多少度?
∠2=∠1=54°(对顶角相等).
因为a∥b,∠1=54°,
所以∠4=∠1=54°(两直线平行,同位角相等),
所以∠3=180°-∠4=126°(邻补角定义).
解:
典题精讲
2
如图,三角形ABC 中,D 是AB上一点,E 是AC上一点,∠ADE = 60°, ∠B=60°,∠AED=60°.
(1)DE 和BC 平行吗?为什么?
(2)∠C 是多少度?为什么?
(1)DE 和BC 平行.因为∠ADE=∠B=60°,所以DE∥BC (同位角相等,两直线平行).
(2)∠C=40°.因为DE∥BC,所以∠C=∠AED=40°(两直线平行,同位角相等).
解:
A
C
典题精讲
3
如图,直线a,b 被直线c 所截,若直线a∥b,∠1=108°,则∠2的度数为( )
A.108°
B.82°
C.72°
D.62°
C
典题精讲
4
如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=50°,则∠2的度数为( ).
A.50°
B.40°
C.30°
D.25°
B
典题精讲
5
如图,AB∥DE,FG⊥BC 于F,∠CDE=40°,则∠FGB= ( )
A.40°
B.50°
C.60°
D.70°
B
典题精讲
6
如图,直线a∥b,∠1=60°,∠2=40°,则∠3等于( )
A.40°
B.60°
C.80°
D.100°
C
探索新知
2
知识点
“内错角”的性质
性质2 两条平行线被第三条直线所截,内错角相等.
两条平行线被第三条直线截得的内错角会具有怎样的数量关系?
探索新知
表达方式:如图因为a∥b(已知),
所以∠1=∠2(两直线平行,内错角相等).
探索新知
例3 如图,MN,EF 表示两面互相平行的镜面,一
束光线AB 照射到镜面MN上,反射光线为BC,
此时∠1=∠2,光线BC 经过镜面EF 反射后的
光线为CD,此时∠3=∠4,试判断AB 与CD 的
位置关系,并说明理由.
探索新知
导引:要判断AB与CD的位置关系,应从两直线的位置关系的
特殊情况,如平行或垂直方面思考问题,观察图可知,
AB与CD 没有交点,所以可猜想AB∥CD,要说明
AB∥CD,只要说明∠ABC=∠BCD 即可.
探索新知
解:AB∥CD,理由如下:
∵MN∥EF,
∴∠2=∠3(两直线平行,内错角相等).
∵∠1=∠2,∠2=∠3,∠3=∠4,
∴∠1+∠2=∠3+∠4.
∵∠1+∠ABC+∠2=180°,
∠3+∠BCD+∠4=180°,
∴∠ABC=∠BCD.
∴AB∥CD(内错角相等,两直线平行).
探索新知
总 结
(1)利用平行线的性质解决实际问题时,其关键是根
据实际问题建立数学模型;
(2)判断两直线的位置关系时,一般都从两直线平行
或垂直这两种特殊情况去思考.
典题精讲
1
如图,已知a∥b,小华把三角板的直角顶点放在直线b上.若∠1=40°,则∠2的度数为( ).
A.100°
B.110°
C.120°
D.130°
D
典题精讲
2
已知直线m∥n,将一块含30°角的直角三角尺ABC 按如图方式放置(∠ABC=30°),其中A,B 两点分别落在m,n上,若∠1=20°,则∠2的度数为( )
A.20°
B.30°
C.45°
D.50°
D
探索新知
3
知识点
“同旁内角”的性质
“同旁内角”的性质:
性质3 两条平行线被第三条直线所截,同旁内角互补.
探索新知
表达方式:如图,因为a∥b(已知),
所以∠1+∠2=180°(两直线平行,同旁内角互补).
探索新知
例4 如图,如果AB∥DF,DE∥BC,且∠1=65°,那么你能说出∠2,∠3,∠4的度数吗?为什么?
导引:由DE∥BC,可得∠1=∠4,∠1+∠2=180°;由DF∥AB,可得∠3=∠2,从而得∠2,∠3,∠4的度数.
探索新知
解:∵DE∥BC (已知),
∴∠4=∠1=65°(两直线平行,内错角相等),
∠2+∠1=180°(两直线平行,同旁内角互补).
∴∠2=180°-∠1=180°-65°=115°.
又∵DF∥AB (已知),
∴∠3=∠2(两直线平行,同位角相等).
∴∠3=115°(等量代换).
探索新知
总 结
1.求角的度数的基本思路:根据平行线的判定由角的数量
关系得到直线的位置关系,根据平行线的性质由直线的
位置关系得到角的数量关系,通过上述相互转化,从而
找到所求角与已知角之间的关系.
2.两直线平行时,应联想到平行线的三个性质,由两条直
线平行的位置关系得到两个相关角的数量关系,由角的
关系求相应角的度数.
典题精讲
1
如图所示,要在一条公路的两侧铺设平行管道,已知一侧铺设的角度为120°,为使管道对接,另一侧铺设的角度大小应为( )
A.120°
B.100°
C.80°
D.60°
D
典题精讲
2
如图,已知a∥b,直角三角尺的直角顶点在直线b上,若∠1=60°,则下列结论错误的是( )
A.∠2=60°
B.∠3=60°
C.∠4=120°
D.∠5=40°
D
易错提醒
已知∠1与∠2是同旁内角.若∠1=50°,则∠2的度数是( )
A.50° B.130°
C.50°或130° D.不能确定
D
易错点:利用平行线的性质时易忽视两直线平行这
一前提而出错.
学以致用
小试牛刀
如图,已知a∥b,∠1=50°,∠2=90°,则∠3的度数为( )
A.40°
B.50°
C.150°
D.140°
D
1
小试牛刀
如图,已知AB∥CD∥EF,FC 平分∠AFE,∠C=25°,则∠A的度数是( )
A.25°
B.35°
C.45°
D.50°
D
2
小试牛刀
如图,AB∥CD,点E 是CD上一点,∠AEC=42°,EF 平分∠AED 交AB 于点F,求∠AFE 的度数.
解:
∵∠AEC=42°,∠AEC+∠AED=180°,
∴∠AED=180°-∠AEC=138°.
∵EF 平分∠AED,
∴∠DEF= ∠AED=69°.
又∵AB∥CD,∴∠AFE=∠DEF=69°.
3
小试牛刀
如图,已知AD⊥BC 于D,EG⊥BC 于G,∠E=∠3.
AD 是∠BAC 的平分线吗?若是,请说明理由.
解:
AD 是∠BAC 的平分线.理由如下:
∵AD⊥BC,EG⊥BC,∴EG∥AD.
∴∠3=∠1,∠E=∠2.
又∵∠E=∠3,
∴∠1=∠2,
即AD 是∠BAC 的平分线.
4
小试牛刀
如图:已知AB∥CD,EF⊥AB 于点O,∠FGC=125°,
求∠EFG 的度数.
下面提供三种思路:
(1)过点F 作FH∥AB;
(2)延长EF 交CD 于M;
(3)延长GF 交AB 于K.
请你利用三个思路中的两个思路,将图形补充完整,
求∠EFG 的度数.
小试牛刀
解:
(一)利用思路(1).
过点F 作FH∥AB,如图①.
∵EF⊥AB,∴∠BOF=90°,
∵FH∥AB,∴∠HFO=∠BOF=90°,
∵AB∥CD,∴FH∥CD,∴∠FGC+∠GFH=180°,
∵∠FGC=125°,∴∠GFH=55°,
∴∠EFG=∠GFH+∠HFO=55°+90°=145°;
小试牛刀
(二)利用思路(2).延长EF 交CD 于点M,如图②.
∵EF⊥AB,∴∠BOF=90°,
∵CD∥AB,∴∠CMF=∠BOF=90°,
∵∠FGC=125°,∴∠1=55°,
∵∠1+∠2+∠GMF=180°,
∴∠2=35°,∵∠GFO+∠2=180°,
∴∠GFO=145°,即∠EFG=145°.
小试牛刀
直线AB∥CD,点P 是直线AB,CD 外的任意一点,连接PA,PC.
(1)探究猜想:
①如图①,若∠A=30°,∠C=40°,则∠APC=________°;
②如图①,若∠A=40°,∠C=60°,则∠APC =________°;
70
100
小试牛刀
解:
③∠APC=∠A+∠C.理由如下:
过P 点向左侧作PE∥AB,则∠APE=∠A,
∵AB∥CD,∴PE∥CD,
∴∠CPE=∠C.
又∵∠APC=∠APE+∠CPE,
∴∠APC=∠A+∠C.
③猜想图①中∠A,∠C,∠APC 三者之间有怎样的等量关系?并说明理由.
小试牛刀
(2)拓展:
①如图②,若∠A=20°,∠C=50°,则∠APC=________°;
②猜想图③中∠A,∠C,∠APC 三者之间的关系为____________________.
30
∠APC=∠A-∠C
课堂小结
课堂小结
平行线的三个性质:
两直线平行,同位角相等.
两直线平行,内错角相等.
两直线平行,同旁内角互补.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
