【班海精品】人教版(新)七下-5.4 平移【优质课件】
文档属性
| 名称 | 【班海精品】人教版(新)七下-5.4 平移【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-09 00:00:00 | ||
图片预览








文档简介
(共45张PPT)
5.4 平 移
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
看一看
五星红旗冉冉升起
情景导入
汽车沿着笔直的公路行驶
情景导入
窗户沿着滑槽移动
情景导入
电梯上的人
情景导入
上述这些运动现象都给我们带来了怎样一种感觉?
飞机在天空飞行
新课精讲
探索新知
1
知识点
平移的定义
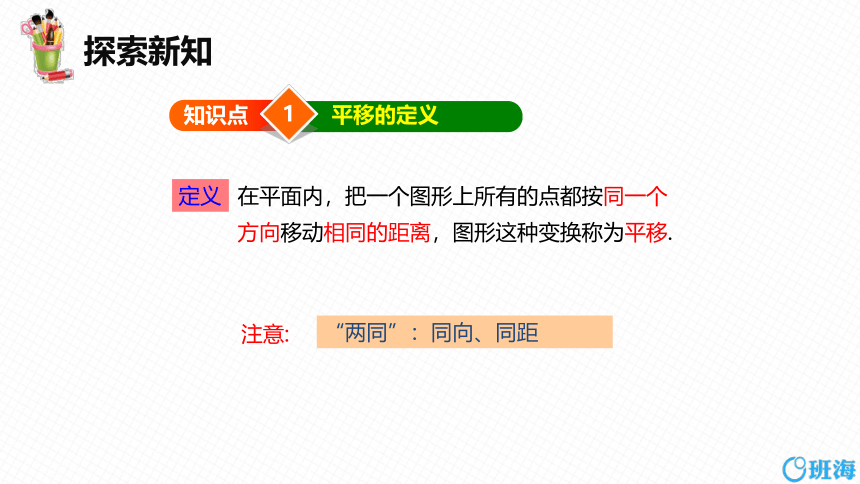
定义
注意:
“两同”:同向、同距
在平面内,把一个图形上所有的点都按同一个方向移动相同的距离,图形这种变换称为平移.
探索新知
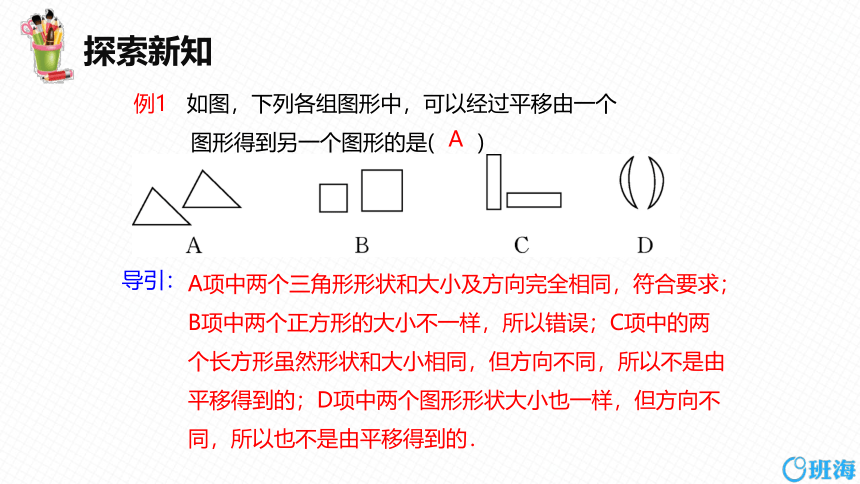
例1 如图,下列各组图形中,可以经过平移由一个
图形得到另一个图形的是( )
A项中两个三角形形状和大小及方向完全相同,符合要求;
B项中两个正方形的大小不一样,所以错误;C项中的两
个长方形虽然形状和大小相同,但方向不同,所以不是由
平移得到的;D项中两个图形形状大小也一样,但方向不
同,所以也不是由平移得到的.
导引:
A
探索新知
总 结
判断一个运动是不是平移现象,要紧扣平移定义的特征:
一变三不变,即图形的位置改变,而图形的形状、大小、方向都不变.
典题精讲
以下现象:①打开教室的门时,门的移动;②打气筒打气时,活塞的运动;③钟摆的摆动;④传送带上,瓶装饮料的移动,其中属于平移的是( )
A.①② B.①③
C.②③ D.②④
1
D
典题精讲
将如图所示的图案平移后,可以得到的图案是( )
2
A
探索新知
2
知识点
平移的性质
(1)平移不改变图形的形状与大小,
它只改变图形在平面中的位置.
平移的性质1:
(2)平移不改变直线的方向.
(保形)
(保向)
探索新知
A
如图,将点A 平移到点A 的位置,
我们把点A 和点A 称为对应点,
把点A 到点A 的方向称为点A 平移的方向,
线段AA 的长度称为点A 平移的距离.
平移的两个要素:
(1)平移的方向
(2)平移的距离
A
把图形平移时,先确定平移的方向,再确定平移的距离.
探索新知
如图,将△ABC 平移到△A B C 的位置,我们把△ABC 和△A B C 称为对应三角形.
其中∠A和∠A 称为对应角.
A
A
B
B
C
C
探索新知
平移的性质2:
一个图形和它经过平移所得的图形中,对应线段平行且相等,对应角相等.
两组对应点的连线平行(或在同一直线上)且相等.
探索新知
如图,图形中有两个梯形ABCD 和EFGH,其中梯形EFGH 是由梯形ABCD 向右平移2 cm后得到的,问:
(1)线段AE,BF,CG,DH 之间有什么数量关系?
(2)AB 与EF,BC 与FG,CD 与GH,AD 与EH 之间有什么关系?
(3)∠BAD 与∠FEH,∠ABC 与∠EFG,∠BCD与∠FGH,∠CDA与∠GHE 之间有什么数量关系?
例2
探索新知
根据平移的特征可知:平移只改变图形的位置,不改变图形的大小;平移得到的图形与原来的图形是完全一样的,所以对应的线段之间是平行且相等的.
(1)线段AE,BF,CG,DH 的长度相等,都为2 cm.
(2)AB 与EF,BC与FG,CD与GH,AD 与EH 分别平行且相等.
(3)∠BAD 与∠FEH,∠ABC 与∠EFG,∠BCD 与∠FGH,∠CDA与∠GHE 对应相等.
解:
导引:
探索新知
总 结
平移中“将一个图形沿着某一直线方向移动一定
的距离”是指图形上的每一点向同一方向平移相同的
距离,就如本题中所提到的“AE,BF,CG,DH ”之
间的位置关系为平行,它们的数量关系为AE=BF=
CG=DH=2 cm.
典题精讲
1
如图,在三角形ABC 中,BC=5 cm,将三角形ABC 沿BC 方向平移至三角形A′B′C′的对应位置时,A′B ′恰好经过AC 的中点O,则三角形ABC 平移的距离为________cm.
2.5
典题精讲
2
下列关于图形平移的说法中,错误的是( )
A.图形上所有点移动的方向都相同
B.图形上所有点移动的距离都相等
C.图形上可能存在不动点
D.对应点所连的线段相等
C
典题精讲
3
如图,将直线l1沿着AB方向平移得到直线l2,若∠1=50°,则∠2的度数是( )
A.40°
B.50°
C.90°
D.130°
B
典题精讲
4
经过平移的图形与原图形的对应点所连的线段的关系是( )
A.平行
B.相等
C.平行(或在同一条直线上)且相等
D.不确定
C
典题精讲
5
如图,将三角形ABC 平移可得到三角形A′B′C ′,则图中平行线共有( )
A.3对
B.4对
C.5对
D.6对
D
典题精讲
6
如图,两个边长为5的正方形拼合成一个长方形,则图中阴影部分的面积是( )
A.5
B.25
C.50
D.以上都不对
B
探索新知
3
知识点
平移作图
平移的画法
P
Q
A
C
B
A'
B'
C'
画图形的平移的关键是:
一、定方向
二、定距离
三、找对应点
四、连线段
探索新知
平移作图的一般步骤:
应分四步——定、找、移、连.
(1)定:确定平移的方向和距离;
(2)找:找出表示图形的关键点(图形的顶点、拐点、连接点);
(3)移:过关键点作平行且相等的线段,得到关键点的对应点;
(4)连:按原图顺次连接对应点.
探索新知
如图 (1),平移三角形ABC,使点A移动到点A′ , 画出平移后的三角形.
例3
探索新知
图形平移后的对应点有什么特征?作出点B 和点C 的对应点B′, C′,能确定三角形A′B′C ′吗?
如图 (2),连接AA′,过点
B 作AA′的平行线 l, 在 l上
截取BB ′ =AA′, 则点B ′就
是点B 的对应点.
分析:
解:
典题精讲
如图,在图形B到图形A的变化过程中,下列描述正确的是( )
A.向上平移2个单位长度,向左平移4个单位长度
B.向上平移1个单位长度,向左平移4个单位长度
C.向上平移2个单位长度,向左平移5个单位长度
D.向上平移1个单位长度,向左平移5个单位长度
1
B
典题精讲
2
如图所示,将三角形ABC 平移到三角形DEF 的位置,则下列结论:①AB∥DE,AD=CF=BE;②∠ACB=∠DEF;③平移的方向是点C 到点E 的方向;④平移距离为线段BE 的长.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
B
易错提醒
如图,在长方形ABCD 中,AC与BD 相交于点O,画出三角形AOB 平移后的图形,其平移方向为射线AD 的方向,平移的距离为线段AD 的长.
解:
图①中的三角形DEC 即为所求.
易错点:不能准确地分析出平移对象.
学以致用
小试牛刀
下列图案只用其中一部分平移就可得到的是( )
B
1
小试牛刀
如图,将三角形ABE 向右平移2 cm得到三角形DCF,如果三角形ABE 的周长是16 cm,那么四边形ABFD 的周长是( )
A.16 cm
B.18 cm
C.20 cm
D.21 cm
C
2
小试牛刀
如图的4个小三角形都是等边三角形,边长为1 cm,你能通过平移三角形ABC 得到其他三角形吗?若能,请说出平移的方向和距离.
解:
将三角形ABC 沿着射线AF 的方向平移1 cm
得三角形FAE;将三角形ABC 沿着射线BD
的方向平移1 cm得三角形ECD;将三角形
ABC平移不能得到三角形AEC.
3
小试牛刀
如图,将直角三角形ABC 沿AB 方向平移得到直角三角形DEF,已知BE=5,EF=8,CG=3,求图中阴影部分的面积.
解:
因为将直角三角形ABC 沿AB 方向平移得
到直角三角形DEF,所以三角形ABC 的
面积与三角形DEF 的面积相等,BC=EF.
所以三角形ABC 的面积-三角形DBG 的面积=三角形DEF 的面积-三角形DBG 的面积.
所以阴影部分的面积与梯形GBEF 的面积相等.因为EF=
8,CG=3,所以BG=BC-CG=EF-CG=5,又因为BE
=5,所以阴影部分的面积为(8+5)×5× =32.5.
4
如图所示,已知在三角形ABC 中,BC=4 cm,把三角形ABC 沿BC 方向平移2 cm得到三角形DEF.问:
(1)图中与∠A相等的角有哪几个?
(2)图中的平行线共有多少组?请分别写出来.
(3)BE∶BC∶BF的值是多少?
小试牛刀
5
解:
(1)∠D,∠EMC 和∠AMD 均与∠A 相等;
(2)两组;AB∥DE,AC∥DF;
(3)由题意,得BE=CF=2 cm.
∵BC=4 cm,∴EC=2 cm,BF=6 cm,
∴BE∶BC∶BF=2∶4∶6=1∶2∶3.
小试牛刀
(1)图①是将线段AB 向右平移1个单位长度,图②是将线段AB 折一下再向右平移1个单位长度,请在图③中画出一条有两个折点的折线向右平移1个单位长度的图形;
(2)若长方形的长为a,宽为b,请分别写出三个图形中除去阴影部分后剩余部分的面积;
(3)如图④,在宽为10 m,长为18 m的长方形菜地上有一条弯曲的小路,小路宽为1 m,求这块菜地的面积.
6
小试牛刀
解:
(1)画图略.
(2)剩余部分的面积均为ab-b.
(3)这块菜地的面积为10×18-10×1=170(m2).
课堂小结
课堂小结
1.平移不改变图形的大小和形状,只改变图形的
位置;图形平移后,对应线段平行(或在同一条
直线上)且相等,对应点的连线平行(或在同一
条直线上)且相等.
2.图形平移的条件:平移方向和平移距离或一个
点平移后的位置.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
5.4 平 移
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
看一看
五星红旗冉冉升起
情景导入
汽车沿着笔直的公路行驶
情景导入
窗户沿着滑槽移动
情景导入
电梯上的人
情景导入
上述这些运动现象都给我们带来了怎样一种感觉?
飞机在天空飞行
新课精讲
探索新知
1
知识点
平移的定义
定义
注意:
“两同”:同向、同距
在平面内,把一个图形上所有的点都按同一个方向移动相同的距离,图形这种变换称为平移.
探索新知
例1 如图,下列各组图形中,可以经过平移由一个
图形得到另一个图形的是( )
A项中两个三角形形状和大小及方向完全相同,符合要求;
B项中两个正方形的大小不一样,所以错误;C项中的两
个长方形虽然形状和大小相同,但方向不同,所以不是由
平移得到的;D项中两个图形形状大小也一样,但方向不
同,所以也不是由平移得到的.
导引:
A
探索新知
总 结
判断一个运动是不是平移现象,要紧扣平移定义的特征:
一变三不变,即图形的位置改变,而图形的形状、大小、方向都不变.
典题精讲
以下现象:①打开教室的门时,门的移动;②打气筒打气时,活塞的运动;③钟摆的摆动;④传送带上,瓶装饮料的移动,其中属于平移的是( )
A.①② B.①③
C.②③ D.②④
1
D
典题精讲
将如图所示的图案平移后,可以得到的图案是( )
2
A
探索新知
2
知识点
平移的性质
(1)平移不改变图形的形状与大小,
它只改变图形在平面中的位置.
平移的性质1:
(2)平移不改变直线的方向.
(保形)
(保向)
探索新知
A
如图,将点A 平移到点A 的位置,
我们把点A 和点A 称为对应点,
把点A 到点A 的方向称为点A 平移的方向,
线段AA 的长度称为点A 平移的距离.
平移的两个要素:
(1)平移的方向
(2)平移的距离
A
把图形平移时,先确定平移的方向,再确定平移的距离.
探索新知
如图,将△ABC 平移到△A B C 的位置,我们把△ABC 和△A B C 称为对应三角形.
其中∠A和∠A 称为对应角.
A
A
B
B
C
C
探索新知
平移的性质2:
一个图形和它经过平移所得的图形中,对应线段平行且相等,对应角相等.
两组对应点的连线平行(或在同一直线上)且相等.
探索新知
如图,图形中有两个梯形ABCD 和EFGH,其中梯形EFGH 是由梯形ABCD 向右平移2 cm后得到的,问:
(1)线段AE,BF,CG,DH 之间有什么数量关系?
(2)AB 与EF,BC 与FG,CD 与GH,AD 与EH 之间有什么关系?
(3)∠BAD 与∠FEH,∠ABC 与∠EFG,∠BCD与∠FGH,∠CDA与∠GHE 之间有什么数量关系?
例2
探索新知
根据平移的特征可知:平移只改变图形的位置,不改变图形的大小;平移得到的图形与原来的图形是完全一样的,所以对应的线段之间是平行且相等的.
(1)线段AE,BF,CG,DH 的长度相等,都为2 cm.
(2)AB 与EF,BC与FG,CD与GH,AD 与EH 分别平行且相等.
(3)∠BAD 与∠FEH,∠ABC 与∠EFG,∠BCD 与∠FGH,∠CDA与∠GHE 对应相等.
解:
导引:
探索新知
总 结
平移中“将一个图形沿着某一直线方向移动一定
的距离”是指图形上的每一点向同一方向平移相同的
距离,就如本题中所提到的“AE,BF,CG,DH ”之
间的位置关系为平行,它们的数量关系为AE=BF=
CG=DH=2 cm.
典题精讲
1
如图,在三角形ABC 中,BC=5 cm,将三角形ABC 沿BC 方向平移至三角形A′B′C′的对应位置时,A′B ′恰好经过AC 的中点O,则三角形ABC 平移的距离为________cm.
2.5
典题精讲
2
下列关于图形平移的说法中,错误的是( )
A.图形上所有点移动的方向都相同
B.图形上所有点移动的距离都相等
C.图形上可能存在不动点
D.对应点所连的线段相等
C
典题精讲
3
如图,将直线l1沿着AB方向平移得到直线l2,若∠1=50°,则∠2的度数是( )
A.40°
B.50°
C.90°
D.130°
B
典题精讲
4
经过平移的图形与原图形的对应点所连的线段的关系是( )
A.平行
B.相等
C.平行(或在同一条直线上)且相等
D.不确定
C
典题精讲
5
如图,将三角形ABC 平移可得到三角形A′B′C ′,则图中平行线共有( )
A.3对
B.4对
C.5对
D.6对
D
典题精讲
6
如图,两个边长为5的正方形拼合成一个长方形,则图中阴影部分的面积是( )
A.5
B.25
C.50
D.以上都不对
B
探索新知
3
知识点
平移作图
平移的画法
P
Q
A
C
B
A'
B'
C'
画图形的平移的关键是:
一、定方向
二、定距离
三、找对应点
四、连线段
探索新知
平移作图的一般步骤:
应分四步——定、找、移、连.
(1)定:确定平移的方向和距离;
(2)找:找出表示图形的关键点(图形的顶点、拐点、连接点);
(3)移:过关键点作平行且相等的线段,得到关键点的对应点;
(4)连:按原图顺次连接对应点.
探索新知
如图 (1),平移三角形ABC,使点A移动到点A′ , 画出平移后的三角形.
例3
探索新知
图形平移后的对应点有什么特征?作出点B 和点C 的对应点B′, C′,能确定三角形A′B′C ′吗?
如图 (2),连接AA′,过点
B 作AA′的平行线 l, 在 l上
截取BB ′ =AA′, 则点B ′就
是点B 的对应点.
分析:
解:
典题精讲
如图,在图形B到图形A的变化过程中,下列描述正确的是( )
A.向上平移2个单位长度,向左平移4个单位长度
B.向上平移1个单位长度,向左平移4个单位长度
C.向上平移2个单位长度,向左平移5个单位长度
D.向上平移1个单位长度,向左平移5个单位长度
1
B
典题精讲
2
如图所示,将三角形ABC 平移到三角形DEF 的位置,则下列结论:①AB∥DE,AD=CF=BE;②∠ACB=∠DEF;③平移的方向是点C 到点E 的方向;④平移距离为线段BE 的长.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
B
易错提醒
如图,在长方形ABCD 中,AC与BD 相交于点O,画出三角形AOB 平移后的图形,其平移方向为射线AD 的方向,平移的距离为线段AD 的长.
解:
图①中的三角形DEC 即为所求.
易错点:不能准确地分析出平移对象.
学以致用
小试牛刀
下列图案只用其中一部分平移就可得到的是( )
B
1
小试牛刀
如图,将三角形ABE 向右平移2 cm得到三角形DCF,如果三角形ABE 的周长是16 cm,那么四边形ABFD 的周长是( )
A.16 cm
B.18 cm
C.20 cm
D.21 cm
C
2
小试牛刀
如图的4个小三角形都是等边三角形,边长为1 cm,你能通过平移三角形ABC 得到其他三角形吗?若能,请说出平移的方向和距离.
解:
将三角形ABC 沿着射线AF 的方向平移1 cm
得三角形FAE;将三角形ABC 沿着射线BD
的方向平移1 cm得三角形ECD;将三角形
ABC平移不能得到三角形AEC.
3
小试牛刀
如图,将直角三角形ABC 沿AB 方向平移得到直角三角形DEF,已知BE=5,EF=8,CG=3,求图中阴影部分的面积.
解:
因为将直角三角形ABC 沿AB 方向平移得
到直角三角形DEF,所以三角形ABC 的
面积与三角形DEF 的面积相等,BC=EF.
所以三角形ABC 的面积-三角形DBG 的面积=三角形DEF 的面积-三角形DBG 的面积.
所以阴影部分的面积与梯形GBEF 的面积相等.因为EF=
8,CG=3,所以BG=BC-CG=EF-CG=5,又因为BE
=5,所以阴影部分的面积为(8+5)×5× =32.5.
4
如图所示,已知在三角形ABC 中,BC=4 cm,把三角形ABC 沿BC 方向平移2 cm得到三角形DEF.问:
(1)图中与∠A相等的角有哪几个?
(2)图中的平行线共有多少组?请分别写出来.
(3)BE∶BC∶BF的值是多少?
小试牛刀
5
解:
(1)∠D,∠EMC 和∠AMD 均与∠A 相等;
(2)两组;AB∥DE,AC∥DF;
(3)由题意,得BE=CF=2 cm.
∵BC=4 cm,∴EC=2 cm,BF=6 cm,
∴BE∶BC∶BF=2∶4∶6=1∶2∶3.
小试牛刀
(1)图①是将线段AB 向右平移1个单位长度,图②是将线段AB 折一下再向右平移1个单位长度,请在图③中画出一条有两个折点的折线向右平移1个单位长度的图形;
(2)若长方形的长为a,宽为b,请分别写出三个图形中除去阴影部分后剩余部分的面积;
(3)如图④,在宽为10 m,长为18 m的长方形菜地上有一条弯曲的小路,小路宽为1 m,求这块菜地的面积.
6
小试牛刀
解:
(1)画图略.
(2)剩余部分的面积均为ab-b.
(3)这块菜地的面积为10×18-10×1=170(m2).
课堂小结
课堂小结
1.平移不改变图形的大小和形状,只改变图形的
位置;图形平移后,对应线段平行(或在同一条
直线上)且相等,对应点的连线平行(或在同一
条直线上)且相等.
2.图形平移的条件:平移方向和平移距离或一个
点平移后的位置.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
