【班海精品】人教版(新)七下-5.1 相交线 第四课时【优质课件】
文档属性
| 名称 | 【班海精品】人教版(新)七下-5.1 相交线 第四课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 7.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-09 17:35:23 | ||
图片预览





文档简介
(共44张PPT)
5.1 相交线
第4课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
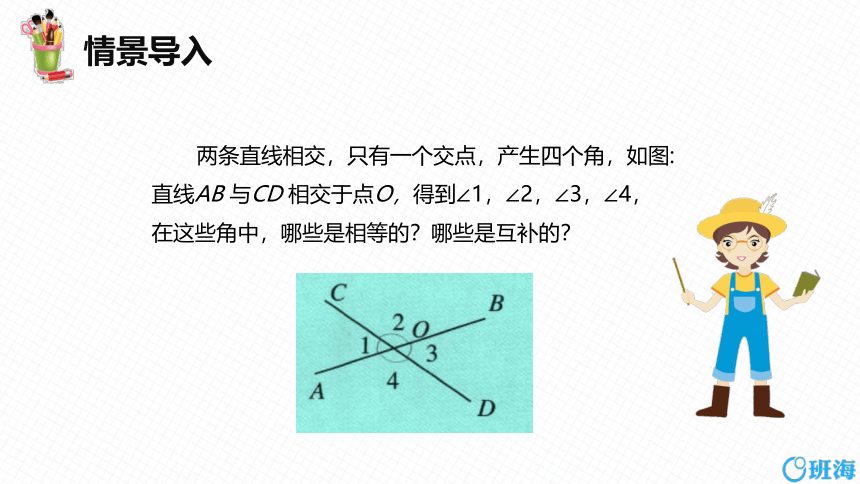
两条直线相交,只有一个交点,产生四个角,如图:
直线AB 与CD 相交于点O,得到∠1,∠2,∠3,∠4,在这些角中,哪些是相等的?哪些是互补的?
情景导入
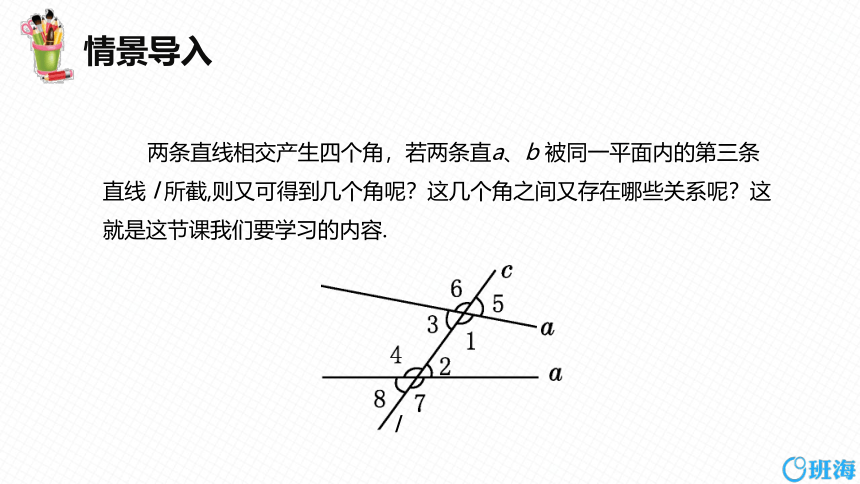
两条直线相交产生四个角,若两条直a、b 被同一平面内的第三条直线 l 所截,则又可得到几个角呢?这几个角之间又存在哪些关系呢?这就是这节课我们要学习的内容.
l
新课精讲
探索新知
1
知识点
同位角
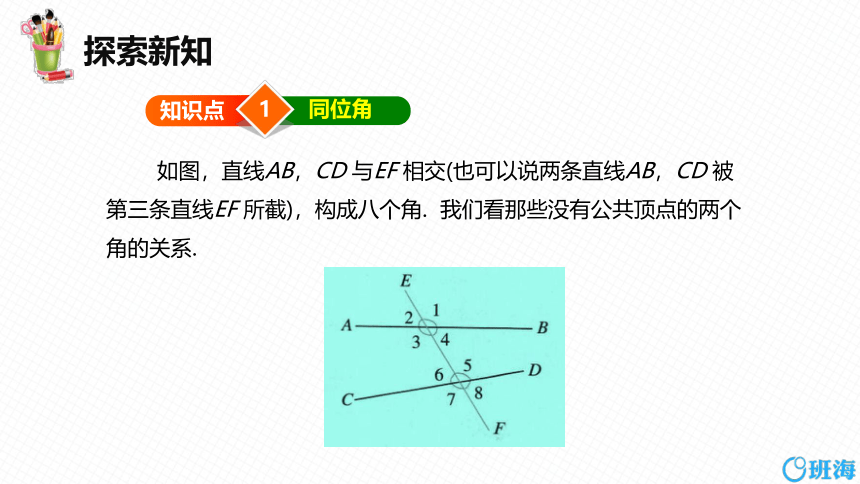
如图,直线AB,CD 与EF 相交(也可以说两条直线AB,CD 被第三条直线EF 所截),构成八个角. 我们看那些没有公共顶点的两个角的关系.
探索新知
A
B
C
D
F
2
3
6
7
8
4
1
5
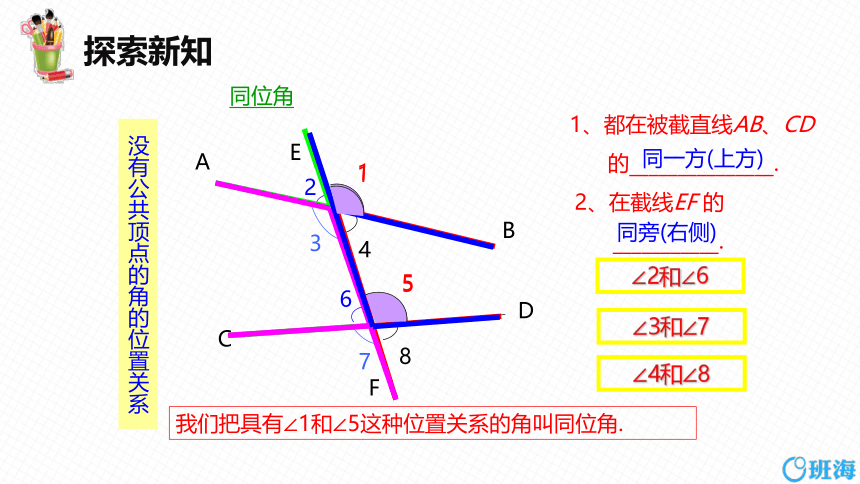
同位角
没有公共顶点的角的位置关系
E
1、都在被截直线AB、CD
的_______________.
2、在截线EF 的
___________.
同一方(上方)
同旁(右侧)
∠2和∠6
∠3和∠7
∠4和∠8
1
5
我们把具有∠1和∠5这种位置关系的角叫同位角.
探索新知
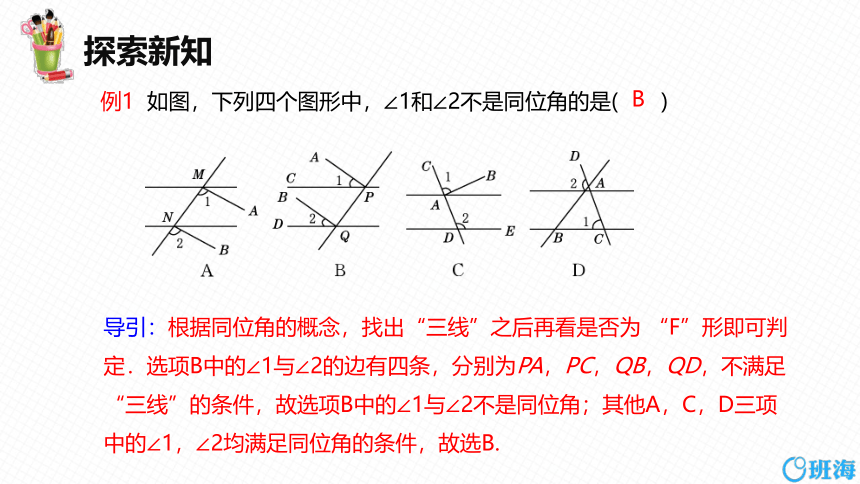
例1 如图,下列四个图形中,∠1和∠2不是同位角的是( )
B
导引:根据同位角的概念,找出“三线”之后再看是否为 “F”形即可判定.选项B中的∠1与∠2的边有四条,分别为PA,PC,QB,QD,不满足“三线”的条件,故选项B中的∠1与∠2不是同位角;其他A,C,D三项中的∠1,∠2均满足同位角的条件,故选B.
探索新知
总 结
判断“三线八角”中的两个角的位置关系时,必须找出“哪两条直线被第三条直线所截”,即找准截线是关键,找截线的实质就是找到相应两个角的顶点所在的直线,如果这两个角的公共边恰好就是截线,那么这两个角就是同位角.
典题精讲
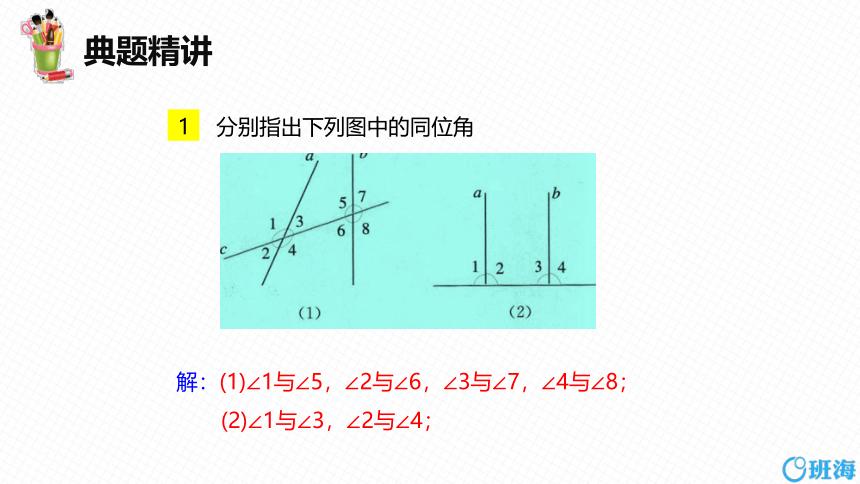
分别指出下列图中的同位角
解:(1)∠1与∠5,∠2与∠6,∠3与∠7,∠4与∠8;
(2)∠1与∠3,∠2与∠4;
典题精讲
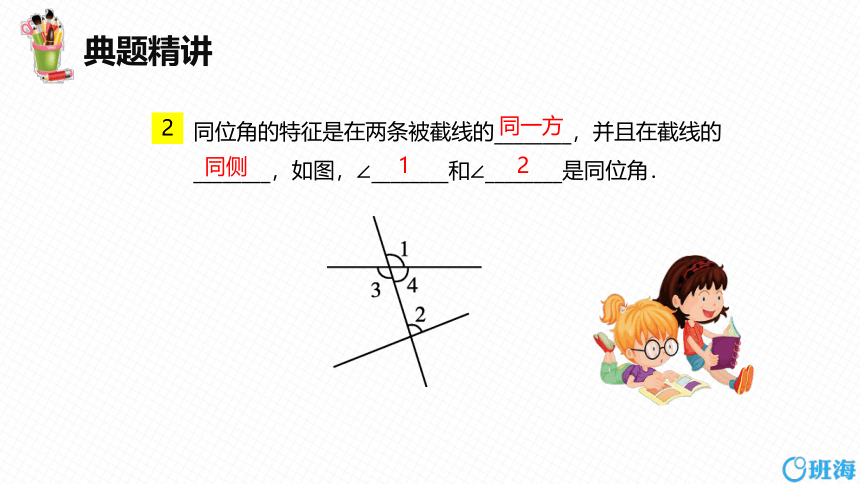
2
同位角的特征是在两条被截线的________,并且在截线的________,如图,∠________和∠________是同位角.
同一方
同侧
1
2
典题精讲
3 如图,在所标识的角中,同位角是( )
A.∠1和∠2 B.∠1和∠3
C.∠1和∠4 D.∠2和∠3
C
典题精讲
4 下列图形中(如图),∠1和∠2是同位角的有( )
A.1个 B.2个 C.3个 D.4个
D
探索新知
2
知识点
内错角
A
B
C
D
E
F
2
7
6
4
没有公共顶点的角的位置关系
内错角
1、它们在被截直线AB、
CD .
2、在截线EF的
___________.
1
8
3
5
两侧(交错)
我们把具有∠3和∠5这种位置关系的角叫内错角.
∠4和∠6
之间(之内)
探索新知
例2 如图,试找出图中与∠2是同位角、内错角的角.
导引:在AF 和AG 被DE 所截的这个基本图形中,可以
看出∠6和∠2处于“同一个位置”,因此,
∠2的同位角为∠6,∠2和∠8是内错角.
解: ∠2的同位角为∠6,∠2的内错角为∠8.
探索新知
总 结
寻找一个角的同位角、内错角,首先应该把这个角放在一个“三线八角”的基本图形中,其次不管是同位角,还是内错角,它们具有一个共同特征,这两个角有一对边在同一直线上,这条直线就是定义中的“第三条直线”,而这两个角剩下的两边所在的直线就是两条被截的直线 ;最后看这两个角的位置特征是否满足同位角、内错角的位置特征:三边成“F ” 、“Z ”形.
典题精讲
分别指出下列图中的内错角
解:(1)∠3与∠6,∠4与∠5;
(2)无内错角.
典题精讲
2 如图,两只手的食指和大拇指在同一个平面内,它们构成的一对角可看成是__________.
内错角
典题精讲
3 如图,∠1的内错角是( )
A.∠2 B.∠3 C.∠4 D.∠5
D
探索新知
3
知识点
同旁内角
A
B
C
D
E
F
2
7
6
没有公共顶点的角的位置关系
同旁内角
1、它们在两条被截直线AB、
CD_____________.
2、在截线EF 的
____________.
1
8
4
5
3
6
之间(之内)
同一旁(同侧)
我们把具有∠3和∠6这种位置关系的角叫同旁内角.
∠4和∠6
探索新知
如图,直线DE,BC 被直线 AB 所截.
(1)∠1和∠2, ∠1和∠3, ∠1和∠4 各是什么位置关系的角?
(2) 如果∠1=∠4,那么∠1和∠2相等吗?
∠1和∠3互补吗?为什么?
例3
探索新知
∠1和∠2是内错角, ∠1和∠3是同旁内角,
∠1和∠4是同位角.
(2)如果∠1=∠4,由对顶角相等,得∠2=∠4,
那么∠1=∠2.
因为∠4=∠3互补,即∠4 + ∠3 = 180°,
又因为∠1 = ∠4,所以∠1 + ∠3 = 180°,
即∠1和∠3 互补.
答:
探索新知
总 结
本题运用定义法. 识别同位角、内错角、同旁内角的关键是看两个角所涉及直线是否只有三条,并且有没有一条边在同一直线(截线)上,如果没有,就不是;如果有,再根据角的位置特征判断.
典题精讲
分别指出下列图中的同旁内角
解:(1)∠3与∠5,∠4与∠6;
(2) ∠2与∠3.
典题精讲
如图,∠B 与哪个角是内错角,与哪个角是同旁内角?它们分别是哪两条直线被哪一条直线所截形成的?对∠C 进行同样的讨论.
∠B 与∠BAD 是内错角,∠B 与∠BAE 是同旁内角,它们都是直线BC,DE 被
直线AB所截形成的.
2
解:
典题精讲
∠C 与∠CAE 是内错角,∠C 与∠CAD 是同旁内角,它们都是直线BC,DE 被直线AC 所截形成的. 另外,∠B 与∠C 也是同旁内角,它们是直线AB,AC 被直线BC 所截形成的.∠B 与∠BAC 是同旁内角,它们是直线AC,BC 被直线AB 所截形成的 . ∠C 与∠BAC 是同旁内角,它们是直线AB,BC 被直线AC 所截形成的.
典题精讲
3
如图,与∠1是同旁内角的是( ).
A.∠2
B.∠3
C.∠4
D.∠5
D
典题精讲
4
如图,直线a,b被c所截,则∠1与∠2是( ).
A.同位角
B.内错角
C.同旁内角
D.邻补角
B
典题精讲
5
如图,与∠1互为同旁内角的角共有( )个.
A.1
B.2
C.3
D.4
C
易错提醒
如图,找出图中所能表示的角中所有与∠1是同位角、内错角和同旁内角的角.
解:
∠1没有同位角,∠1的内错角是∠2,∠1的同旁内角有∠6,∠7,∠ABC.
易错点:对三种角的定义理解不透彻而漏解.
学以致用
小试牛刀
如图,图中共有( )对同位角.
A.2
B.4
C.6
D.8
B
1
小试牛刀
2 在我们常见的英文字母中,也存在着同位角、内错角、同旁内角,在下面几个字母中,含有内错角最少的字母是( )
C
小试牛刀
如图,下列说法正确的是( )
A.∠2和∠B 是同位角
B.∠2和∠B 是内错角
C.∠1和∠A 是内错角
D.∠3和∠B 是同旁内角
D
3
小试牛刀
4 如图,∠1和∠2,∠3和∠4分别是由哪两条直线被哪一条直线所截形成的?它们各是什么角?
题图①中,∠1和∠2是直线AB与CD 被直线BD 所截形成的内错角,∠3和∠4是直线AD 与BC 被直线BD 所截形成的内错角.题图②中,∠1和∠2是直线AB 与CD 被直线BC 所截形成的同位角,∠3和∠4是直线AB与BC 被直线AC 所截形成的同旁内角.
小试牛刀
5 两条直线被第三条直线所截,∠1和∠2是同旁内角,∠3和∠2是内错角.
(1)根据上述条件,画出符合题意的示意图;
(2)若∠1=3∠2,∠2=3∠3,求∠1,∠2的度数.
解:
(1)如图.
(2)因为∠1=3∠2,∠2=3∠3,
所以∠1=9∠3.
又因为∠1+∠3=180°,
所以∠3=18°.
所以∠1=162°,∠2=54°.
小试牛刀
6 如图,直线DE,BC 被直线AB,AC 所截.
(1)∠2与∠B 是什么角?若∠1=∠B,则∠2与∠B 有何数量关系?请说明理由.
(2)∠3与∠C 是什么角?若∠4+∠C=180°,则∠3与∠C 有何数量关系?请说明理由.
小试牛刀
解:
(1)同旁内角.∠2+∠B=180°.
理由:因为∠1+∠2=180°,∠1=∠B,
所以∠2+∠B=180°.
(2)同位角.∠3=∠C.
理由:因为∠4+∠3=180°,
∠4+∠C=180°,所以∠3=∠C.
小试牛刀
图形编号 ① ② ③ …
同位角对数 …
内错角对数 …
同旁内角对数 …
7 下列各图(如图),都是水平直线被一条倾斜的直线所截:
(1)请观察并填写下表:
4
12
24
2
6
12
2
6
12
小试牛刀
(2)若n 条水平直线被一条倾斜直线所截,请用含n 的式子表
示同位角、内错角、同旁内角的对数.
同位角对数:2n(n-1),内错角对数:n(n-1),同旁内角对数:n(n-1).
解:
课堂小结
课堂小结
内部同侧
在两条被截直线内部,在截线的同侧
同旁内角
内部异侧
在两条被截直线内部,在截线的异侧(交错)
内错角
同旁同侧
同位角
图形结构特征
位置特征
角的名称
在两条被截直线同旁,
在截线的同侧
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
5.1 相交线
第4课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
两条直线相交,只有一个交点,产生四个角,如图:
直线AB 与CD 相交于点O,得到∠1,∠2,∠3,∠4,在这些角中,哪些是相等的?哪些是互补的?
情景导入
两条直线相交产生四个角,若两条直a、b 被同一平面内的第三条直线 l 所截,则又可得到几个角呢?这几个角之间又存在哪些关系呢?这就是这节课我们要学习的内容.
l
新课精讲
探索新知
1
知识点
同位角
如图,直线AB,CD 与EF 相交(也可以说两条直线AB,CD 被第三条直线EF 所截),构成八个角. 我们看那些没有公共顶点的两个角的关系.
探索新知
A
B
C
D
F
2
3
6
7
8
4
1
5
同位角
没有公共顶点的角的位置关系
E
1、都在被截直线AB、CD
的_______________.
2、在截线EF 的
___________.
同一方(上方)
同旁(右侧)
∠2和∠6
∠3和∠7
∠4和∠8
1
5
我们把具有∠1和∠5这种位置关系的角叫同位角.
探索新知
例1 如图,下列四个图形中,∠1和∠2不是同位角的是( )
B
导引:根据同位角的概念,找出“三线”之后再看是否为 “F”形即可判定.选项B中的∠1与∠2的边有四条,分别为PA,PC,QB,QD,不满足“三线”的条件,故选项B中的∠1与∠2不是同位角;其他A,C,D三项中的∠1,∠2均满足同位角的条件,故选B.
探索新知
总 结
判断“三线八角”中的两个角的位置关系时,必须找出“哪两条直线被第三条直线所截”,即找准截线是关键,找截线的实质就是找到相应两个角的顶点所在的直线,如果这两个角的公共边恰好就是截线,那么这两个角就是同位角.
典题精讲
分别指出下列图中的同位角
解:(1)∠1与∠5,∠2与∠6,∠3与∠7,∠4与∠8;
(2)∠1与∠3,∠2与∠4;
典题精讲
2
同位角的特征是在两条被截线的________,并且在截线的________,如图,∠________和∠________是同位角.
同一方
同侧
1
2
典题精讲
3 如图,在所标识的角中,同位角是( )
A.∠1和∠2 B.∠1和∠3
C.∠1和∠4 D.∠2和∠3
C
典题精讲
4 下列图形中(如图),∠1和∠2是同位角的有( )
A.1个 B.2个 C.3个 D.4个
D
探索新知
2
知识点
内错角
A
B
C
D
E
F
2
7
6
4
没有公共顶点的角的位置关系
内错角
1、它们在被截直线AB、
CD .
2、在截线EF的
___________.
1
8
3
5
两侧(交错)
我们把具有∠3和∠5这种位置关系的角叫内错角.
∠4和∠6
之间(之内)
探索新知
例2 如图,试找出图中与∠2是同位角、内错角的角.
导引:在AF 和AG 被DE 所截的这个基本图形中,可以
看出∠6和∠2处于“同一个位置”,因此,
∠2的同位角为∠6,∠2和∠8是内错角.
解: ∠2的同位角为∠6,∠2的内错角为∠8.
探索新知
总 结
寻找一个角的同位角、内错角,首先应该把这个角放在一个“三线八角”的基本图形中,其次不管是同位角,还是内错角,它们具有一个共同特征,这两个角有一对边在同一直线上,这条直线就是定义中的“第三条直线”,而这两个角剩下的两边所在的直线就是两条被截的直线 ;最后看这两个角的位置特征是否满足同位角、内错角的位置特征:三边成“F ” 、“Z ”形.
典题精讲
分别指出下列图中的内错角
解:(1)∠3与∠6,∠4与∠5;
(2)无内错角.
典题精讲
2 如图,两只手的食指和大拇指在同一个平面内,它们构成的一对角可看成是__________.
内错角
典题精讲
3 如图,∠1的内错角是( )
A.∠2 B.∠3 C.∠4 D.∠5
D
探索新知
3
知识点
同旁内角
A
B
C
D
E
F
2
7
6
没有公共顶点的角的位置关系
同旁内角
1、它们在两条被截直线AB、
CD_____________.
2、在截线EF 的
____________.
1
8
4
5
3
6
之间(之内)
同一旁(同侧)
我们把具有∠3和∠6这种位置关系的角叫同旁内角.
∠4和∠6
探索新知
如图,直线DE,BC 被直线 AB 所截.
(1)∠1和∠2, ∠1和∠3, ∠1和∠4 各是什么位置关系的角?
(2) 如果∠1=∠4,那么∠1和∠2相等吗?
∠1和∠3互补吗?为什么?
例3
探索新知
∠1和∠2是内错角, ∠1和∠3是同旁内角,
∠1和∠4是同位角.
(2)如果∠1=∠4,由对顶角相等,得∠2=∠4,
那么∠1=∠2.
因为∠4=∠3互补,即∠4 + ∠3 = 180°,
又因为∠1 = ∠4,所以∠1 + ∠3 = 180°,
即∠1和∠3 互补.
答:
探索新知
总 结
本题运用定义法. 识别同位角、内错角、同旁内角的关键是看两个角所涉及直线是否只有三条,并且有没有一条边在同一直线(截线)上,如果没有,就不是;如果有,再根据角的位置特征判断.
典题精讲
分别指出下列图中的同旁内角
解:(1)∠3与∠5,∠4与∠6;
(2) ∠2与∠3.
典题精讲
如图,∠B 与哪个角是内错角,与哪个角是同旁内角?它们分别是哪两条直线被哪一条直线所截形成的?对∠C 进行同样的讨论.
∠B 与∠BAD 是内错角,∠B 与∠BAE 是同旁内角,它们都是直线BC,DE 被
直线AB所截形成的.
2
解:
典题精讲
∠C 与∠CAE 是内错角,∠C 与∠CAD 是同旁内角,它们都是直线BC,DE 被直线AC 所截形成的. 另外,∠B 与∠C 也是同旁内角,它们是直线AB,AC 被直线BC 所截形成的.∠B 与∠BAC 是同旁内角,它们是直线AC,BC 被直线AB 所截形成的 . ∠C 与∠BAC 是同旁内角,它们是直线AB,BC 被直线AC 所截形成的.
典题精讲
3
如图,与∠1是同旁内角的是( ).
A.∠2
B.∠3
C.∠4
D.∠5
D
典题精讲
4
如图,直线a,b被c所截,则∠1与∠2是( ).
A.同位角
B.内错角
C.同旁内角
D.邻补角
B
典题精讲
5
如图,与∠1互为同旁内角的角共有( )个.
A.1
B.2
C.3
D.4
C
易错提醒
如图,找出图中所能表示的角中所有与∠1是同位角、内错角和同旁内角的角.
解:
∠1没有同位角,∠1的内错角是∠2,∠1的同旁内角有∠6,∠7,∠ABC.
易错点:对三种角的定义理解不透彻而漏解.
学以致用
小试牛刀
如图,图中共有( )对同位角.
A.2
B.4
C.6
D.8
B
1
小试牛刀
2 在我们常见的英文字母中,也存在着同位角、内错角、同旁内角,在下面几个字母中,含有内错角最少的字母是( )
C
小试牛刀
如图,下列说法正确的是( )
A.∠2和∠B 是同位角
B.∠2和∠B 是内错角
C.∠1和∠A 是内错角
D.∠3和∠B 是同旁内角
D
3
小试牛刀
4 如图,∠1和∠2,∠3和∠4分别是由哪两条直线被哪一条直线所截形成的?它们各是什么角?
题图①中,∠1和∠2是直线AB与CD 被直线BD 所截形成的内错角,∠3和∠4是直线AD 与BC 被直线BD 所截形成的内错角.题图②中,∠1和∠2是直线AB 与CD 被直线BC 所截形成的同位角,∠3和∠4是直线AB与BC 被直线AC 所截形成的同旁内角.
小试牛刀
5 两条直线被第三条直线所截,∠1和∠2是同旁内角,∠3和∠2是内错角.
(1)根据上述条件,画出符合题意的示意图;
(2)若∠1=3∠2,∠2=3∠3,求∠1,∠2的度数.
解:
(1)如图.
(2)因为∠1=3∠2,∠2=3∠3,
所以∠1=9∠3.
又因为∠1+∠3=180°,
所以∠3=18°.
所以∠1=162°,∠2=54°.
小试牛刀
6 如图,直线DE,BC 被直线AB,AC 所截.
(1)∠2与∠B 是什么角?若∠1=∠B,则∠2与∠B 有何数量关系?请说明理由.
(2)∠3与∠C 是什么角?若∠4+∠C=180°,则∠3与∠C 有何数量关系?请说明理由.
小试牛刀
解:
(1)同旁内角.∠2+∠B=180°.
理由:因为∠1+∠2=180°,∠1=∠B,
所以∠2+∠B=180°.
(2)同位角.∠3=∠C.
理由:因为∠4+∠3=180°,
∠4+∠C=180°,所以∠3=∠C.
小试牛刀
图形编号 ① ② ③ …
同位角对数 …
内错角对数 …
同旁内角对数 …
7 下列各图(如图),都是水平直线被一条倾斜的直线所截:
(1)请观察并填写下表:
4
12
24
2
6
12
2
6
12
小试牛刀
(2)若n 条水平直线被一条倾斜直线所截,请用含n 的式子表
示同位角、内错角、同旁内角的对数.
同位角对数:2n(n-1),内错角对数:n(n-1),同旁内角对数:n(n-1).
解:
课堂小结
课堂小结
内部同侧
在两条被截直线内部,在截线的同侧
同旁内角
内部异侧
在两条被截直线内部,在截线的异侧(交错)
内错角
同旁同侧
同位角
图形结构特征
位置特征
角的名称
在两条被截直线同旁,
在截线的同侧
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
