【班海精品】人教版(新)七下-5.1 相交线 第二课时【优质课件】
文档属性
| 名称 | 【班海精品】人教版(新)七下-5.1 相交线 第二课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-09 17:35:23 | ||
图片预览










文档简介
(共45张PPT)
5.1 相交线
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
如图所示是北京天安门广场庄严隆重的升国旗仪式,是亿万中国人民特别关注的活动.众所周知,1949年10月1日,毛泽东主席在天安门城楼上用洪亮的声音向全世界宣告中华人民共和国诞生,亲手升起了第一面五星红旗.
情景导入
天安门广场的升国旗仪式一招一式欣赏性极强,人们概括有“五绝”.一绝:升旗;二绝:护旗;三绝:敬礼;四绝:礼毕;五绝:收旗.其中的每招每式都有极其严格的要求.每一次,当擎旗手以优美的动作,在国歌奏响第一个音符时,将国旗展开抛出,到国歌的最后一个音符终止,都是2分07秒,国旗也准时到达30米高的旗杆顶端,做到了分秒不差.可是,你看着旗杆与地面,会想到旗杆与地面有怎样的位置关系呢?
新课精讲
探索新知
当转动一木条的位置时,什么也随着发生了变化?
观察思考
1
知识点
垂直的定义
探索新知
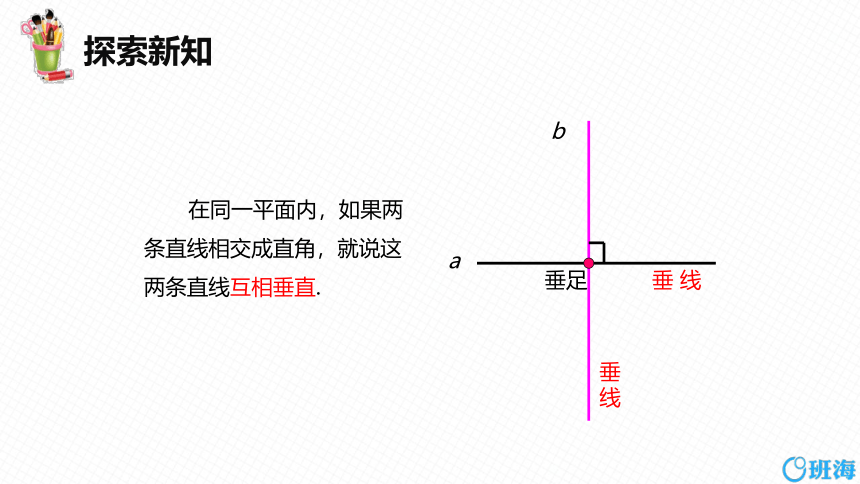
a
在同一平面内,如果两条直线相交成直角,就说这两条直线互相垂直.
垂足
垂 线
垂
线
b
探索新知
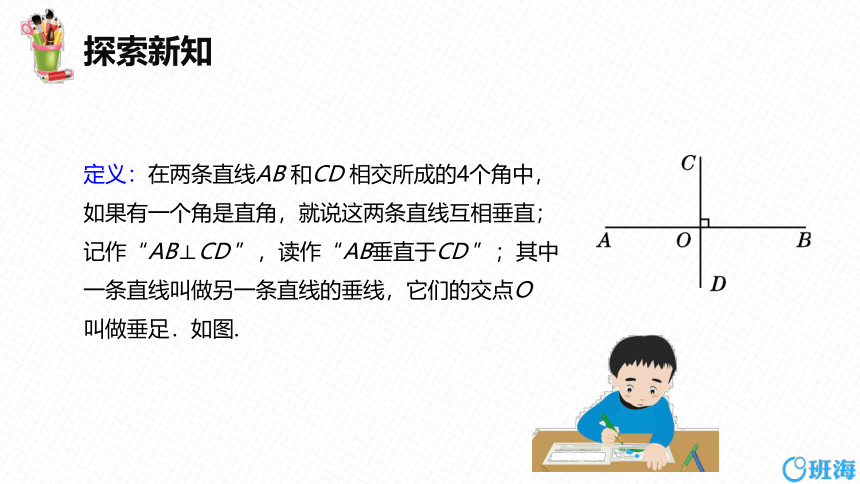
定义:在两条直线AB 和CD 相交所成的4个角中,
如果有一个角是直角,就说这两条直线互相垂直;
记作“AB⊥CD ”,读作“AB垂直于CD ”;其中
一条直线叫做另一条直线的垂线,它们的交点O
叫做垂足.如图.
探索新知
要判断OE,OF 是什么位置关系,其实质是说明OE,OF 是否垂直,即要看∠EOF 是否为90°;要让∠EOF=90°,需说明∠EOF=∠AOC 或∠EOF=∠BOC 都可,这样就把问题转化为说明∠AOE=∠COF (已知)了.
如图,CO⊥AB 于点O,∠AOE=∠COF,则射线OE, OF 是什么位置关系?请说明理由.
导引:
例1
探索新知
解:射线OE,OF 互相垂直.理由如下:
因为CO⊥AB,所以∠AOC=90°.
又因为∠AOE=∠COF,
所以∠AOE+∠COE=∠COF+∠COE,
即∠AOC=∠EOF=90°.
所以OE 与OF 互相垂直(垂直定义).
探索新知
总 结
判断两直线(线段、射线所在直线)互相垂直,主要
依据是垂直定义,只要说明两条相交直线所构成的四
个角中有一个角是直角即可.
探索新知
根据∠AOC 与∠BOD 是对顶角,且∠BOD 与∠BOE 互余,即可求出∠AOC 的度数;根据OD 平分∠BOF,∠EOF=∠BOE+∠BOF 即可求出∠EOF 的度数;根据∠AOF 与∠BOF 互补可求得∠AOF 的度数.
如图,直线AB,CD 相交于点O,过O 点画射线OE,OF,使OE⊥CD,OD 平分∠BOF.如果∠BOE=50°,求∠AOC,∠EOF 和∠AOF 的度数.
导引:
例2
探索新知
解:因为OE⊥CD,所以∠DOE=90°(垂直定义).
因为∠BOE=50°,
所以∠AOC=∠BOD=∠DOE-∠BOE=
90°-50°=40°.
因为OD 平分∠BOF,
所以∠BOF=2∠BOD=80°.
所以∠EOF=∠BOF+∠BOE=80°+50°=130°,
∠AOF=∠AOB-∠BOF=180°-80°=100°.
典题精讲
1
当两条直线相交所成的四个角都相等时,这两条直线有什么位置关系?为什么?
当两条直线相交,所成的四个角都相等时,这两条直线互相垂直.理由:设所成的四个角中有一个角的度数为m°,则其余三个角的度数分别为180°-m°,m°,180°-m°,由题意知,m°=180°-m°,得m°=90°,所以180°-m°=90°,所以这两条直线互相垂直.
解:
典题精讲
如图,已知点O 在直线AB上,CO⊥DO 于点O,若∠1=145°,则∠3的度数为( )
A.35°
B.45°
C.55°
D.65°
2
C
如图,三条直线相交于点O,若CO⊥AB,∠1=56°,则∠2等于( )
A.30°
B.34°
C.45°
D.56°
典题精讲
3
B
典题精讲
如图,点O 在直线AB上,且OC⊥OD,若∠COA=36°,则∠DOB 的大小为( )
A.36°
B.54°
C.55°
D.44°
4
B
典题精讲
如图,已知OA⊥OB,OC⊥OD,∠AOC=27°,则∠BOD 的度数是( )
A.117°
B.127°
C.153°
D.163°
5
C
典题精讲
如图,直线AB,CD 相交于点O,射线OM 平分∠AOC,ON⊥OM.若∠AOM=35°,则∠CON 的度数为( )
A.35°
B.45°
C.55°
D.65°
6
C
探索新知
2
知识点
垂线的画法
用三角尺画垂线的方法:
一贴,用三角尺的一条直角边贴住已知直线;
二靠,用三角尺的另一条直角边靠住已知点;
三画,画出垂线. 如果作线段互相垂直或作射线的垂
线,实际上是作线段所在的直线互相垂直,或作射线
所在的直线的垂线,因为射线和线段都是直线的一部
分.在垂线的画法中,有时需延长线段,垂足在延长
线上,并记上直角符号“﹁”.
探索新知
注意:画垂线也可用以下两种方法:
(1)利用量角器画;(2)用折叠法画.
探索新知
例3 如图,M 是三角形ABC 中BC 边上的任意一点,请
你按照下列要求画图:
(1)过M 点画直线AB 的垂线m;
(2)过M 点画直线BC 的垂线n;
(3)过M 点画直线AC 的垂线p.
探索新知
导引:观察图形不难看出,(1)(3)属于过直线外一点画
已知直线的垂线,(2)属于过直线上一点画已知
直线的垂线,所以按照“一靠、二过、三画”
的方法画图即可.
解:画出的直线m,n,p 如上页图.
探索新知
总 结
过已知点画已知直线的垂线,实际上就是过已知点画一条直线,使所画直线与已知直线相交所成的角是90°.
典题精讲
1
画一条线段或射线的垂线,就是画它们所在直线的垂线. 如图,请你过点P画出射线AB 或线段AB 的垂线.
如图所示.
解:
典题精讲
2
下列选项中,过点P 画AB 的垂线CD,三角板放法正确的是( ).
C
探索新知
3
知识点
垂线的性质
探究
如图.
(1)用三角尺或量角器画已知直线l 的垂线,这样的垂线能画出几条
(2)经过直线l 上一点A 画l 的垂线,这样的垂线能画出几条?
(3)经过直线l 外一点B 画l 的垂线,这样的垂线能画出几条?
探索新知
归 纳
经过一点(已知直线上或直线外),能画出已知直线的一条垂线,并且只 能画出一条垂线.即在同一平面内,过一点有且只有一条直线与已知直线垂直.
在平面内,不是在空间内,这是需要注意的条件:其中,一点可以是直线上一点也可以是直线外一点;“有且只有”中的“有”是指能画出一条已知直线的垂线,即存在性,“只有”是指只能画一条,即唯一性.
探索新知
例4 如图,已知直线AB,CB,l 在同一平面内,若AB⊥l,垂足为B,CB⊥l,垂足也为B,则符合题意的图形可以是( )
C
导引:根据题意可知,过点B 有AB,CB 都与直线l 垂直,由垂线的性质可知,在同一平面内,过一点有且只有一条直线与已知直线垂直,所以A、B、C 三点在一条直线上.
探索新知
总 结
利用直线的性质解答题目,要注意直线性质满足的条件:
1. 在平面内;
2. 过一点,点的位置可以在直线上也可以在直线外;
3. 相交所成的角必须是直角,以上三条缺一不可.
典题精讲
在同一平面内,下列语句正确的是( )
A.过一点有无数条直线与已知直线垂直
B.和一条直线垂直的直线有两条
C.过一点有且只有一条直线与已知直线垂直
D.若两直线相交,则它们一定垂直
1
C
易错提醒
(1)在图①中,过AB 外一点M 作AB 的垂线;
(2)在图②中,过点A,B分别作OB,OA 的垂线.
解:
(1)如图①所示.
(2)如图②所示.
易错点:误认为垂足一定要在线段或射线上而导致错误.
学以致用
小试牛刀
已知在同一平面内:
①两条直线相交成直角;
②两条直线互相垂直;
③一条直线是另一条直线的垂线.
那么下列因果关系:①→②③;②→①③;③→①②中,正确的有( )
A.0个 B.1个 C.2个 D.3个
D
1
典题精讲
过一条线段外一点,作这条线段的垂线,垂足在( )
A.这条线段上
B.这条线段的端点处
C.这条线段的延长线上
D.以上都有可能
D
2
小试牛刀
如图,如果直线ON⊥直线a,直线OM⊥直线a,那么OM 与ON 重合(即O,M,N 三点共线),其理由是( ).
A.两点确定一条直线
B.在同一平面内,过两点有且只有一条直线与已
知直线垂直
C.在同一平面内,过一点有且只有一条直线与已
知直线垂直
D.两点之间,线段最短
C
3
小试牛刀
4 在直线AB上任取一点O,过点O 作射线OC,OD,使OC⊥OD,当∠AOC=30°时,∠BOD 的度数是多少?
解:
如图①,当OC,OD 在直线AB 的同侧时,因为OC⊥OD,所以∠COD=90°.因为∠AOC=30°,所以∠BOD=180°-∠COD-∠AOC=60°.如图②,当OC,OD 在直线AB 的一侧时,因为OC⊥OD,所以∠COD=90°.因为∠AOC=30°,所以∠AOD=90°-∠AOC=60°.
所以∠BOD=180°-∠AOD=120°.
小试牛刀
5 已知OA⊥OB,OC⊥OD.
(1)如图①,若∠BOC=50°,求∠AOD 的度数;
(2)如图②,若∠BOC=60°,求∠AOD 的度数;
(3)根据(1)(2)的结果猜想∠AOD与∠BOC 有怎样的关系?并根据图①
说明理由;
(4)如图②,若∠BOC∶∠AOD=7∶29,求∠BOC 和∠AOD 的度数.
小试牛刀
解:
(1)因为OA⊥OB,所以∠AOB=90°,
所以∠AOC=∠AOB-∠BOC=90°-50°=40°.
因为OC⊥OD,所以∠COD=90°,
所以∠AOD=∠AOC+∠COD=40°+90°=130°.
(2)因为OA⊥OB,所以∠AOB=90°.
因为OC⊥OD,所以∠COD=90°,
所以∠AOD=360°-∠AOB-∠BOC-∠COD=
360°-90°-60°-90°=120°.
小试牛刀
(3)∠AOD 与∠BOC 互补.理由如下:
因为OA⊥OB,所以∠AOB=90°,
所以∠AOC=∠AOB-∠BOC=90°-∠BOC.
因为OC⊥OD,所以∠COD=90°,所以∠AOD=∠AOC
+∠COD=90°-∠BOC+90°=180°-∠BOC,所以
∠AOD+∠BOC=180°,即∠AOD 与∠BOC 互补.
(4)由(3)知∠BOC+∠AOD=180°,
又因为∠BOC∶∠AOD=7∶29,
所以∠BOC= ×180°=35°,
∠AOD= ×180°=145°.
小试牛刀
6 (1)在图①中以P为顶点作∠P,使∠P 的两边分别和∠1的两边垂直;
(2)量一量∠P 和∠1的度数,它们之间的数量关系是_________________;
解:
∠1+∠P=180°
(1)如图①所示.
课堂小结
课堂小结
以下几个方面由学生自己总结:
① 垂线的定义及垂直的符号表示;
② 垂线的有关性质;
③ 过一点作已知直线的垂线的方法.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
5.1 相交线
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
如图所示是北京天安门广场庄严隆重的升国旗仪式,是亿万中国人民特别关注的活动.众所周知,1949年10月1日,毛泽东主席在天安门城楼上用洪亮的声音向全世界宣告中华人民共和国诞生,亲手升起了第一面五星红旗.
情景导入
天安门广场的升国旗仪式一招一式欣赏性极强,人们概括有“五绝”.一绝:升旗;二绝:护旗;三绝:敬礼;四绝:礼毕;五绝:收旗.其中的每招每式都有极其严格的要求.每一次,当擎旗手以优美的动作,在国歌奏响第一个音符时,将国旗展开抛出,到国歌的最后一个音符终止,都是2分07秒,国旗也准时到达30米高的旗杆顶端,做到了分秒不差.可是,你看着旗杆与地面,会想到旗杆与地面有怎样的位置关系呢?
新课精讲
探索新知
当转动一木条的位置时,什么也随着发生了变化?
观察思考
1
知识点
垂直的定义
探索新知
a
在同一平面内,如果两条直线相交成直角,就说这两条直线互相垂直.
垂足
垂 线
垂
线
b
探索新知
定义:在两条直线AB 和CD 相交所成的4个角中,
如果有一个角是直角,就说这两条直线互相垂直;
记作“AB⊥CD ”,读作“AB垂直于CD ”;其中
一条直线叫做另一条直线的垂线,它们的交点O
叫做垂足.如图.
探索新知
要判断OE,OF 是什么位置关系,其实质是说明OE,OF 是否垂直,即要看∠EOF 是否为90°;要让∠EOF=90°,需说明∠EOF=∠AOC 或∠EOF=∠BOC 都可,这样就把问题转化为说明∠AOE=∠COF (已知)了.
如图,CO⊥AB 于点O,∠AOE=∠COF,则射线OE, OF 是什么位置关系?请说明理由.
导引:
例1
探索新知
解:射线OE,OF 互相垂直.理由如下:
因为CO⊥AB,所以∠AOC=90°.
又因为∠AOE=∠COF,
所以∠AOE+∠COE=∠COF+∠COE,
即∠AOC=∠EOF=90°.
所以OE 与OF 互相垂直(垂直定义).
探索新知
总 结
判断两直线(线段、射线所在直线)互相垂直,主要
依据是垂直定义,只要说明两条相交直线所构成的四
个角中有一个角是直角即可.
探索新知
根据∠AOC 与∠BOD 是对顶角,且∠BOD 与∠BOE 互余,即可求出∠AOC 的度数;根据OD 平分∠BOF,∠EOF=∠BOE+∠BOF 即可求出∠EOF 的度数;根据∠AOF 与∠BOF 互补可求得∠AOF 的度数.
如图,直线AB,CD 相交于点O,过O 点画射线OE,OF,使OE⊥CD,OD 平分∠BOF.如果∠BOE=50°,求∠AOC,∠EOF 和∠AOF 的度数.
导引:
例2
探索新知
解:因为OE⊥CD,所以∠DOE=90°(垂直定义).
因为∠BOE=50°,
所以∠AOC=∠BOD=∠DOE-∠BOE=
90°-50°=40°.
因为OD 平分∠BOF,
所以∠BOF=2∠BOD=80°.
所以∠EOF=∠BOF+∠BOE=80°+50°=130°,
∠AOF=∠AOB-∠BOF=180°-80°=100°.
典题精讲
1
当两条直线相交所成的四个角都相等时,这两条直线有什么位置关系?为什么?
当两条直线相交,所成的四个角都相等时,这两条直线互相垂直.理由:设所成的四个角中有一个角的度数为m°,则其余三个角的度数分别为180°-m°,m°,180°-m°,由题意知,m°=180°-m°,得m°=90°,所以180°-m°=90°,所以这两条直线互相垂直.
解:
典题精讲
如图,已知点O 在直线AB上,CO⊥DO 于点O,若∠1=145°,则∠3的度数为( )
A.35°
B.45°
C.55°
D.65°
2
C
如图,三条直线相交于点O,若CO⊥AB,∠1=56°,则∠2等于( )
A.30°
B.34°
C.45°
D.56°
典题精讲
3
B
典题精讲
如图,点O 在直线AB上,且OC⊥OD,若∠COA=36°,则∠DOB 的大小为( )
A.36°
B.54°
C.55°
D.44°
4
B
典题精讲
如图,已知OA⊥OB,OC⊥OD,∠AOC=27°,则∠BOD 的度数是( )
A.117°
B.127°
C.153°
D.163°
5
C
典题精讲
如图,直线AB,CD 相交于点O,射线OM 平分∠AOC,ON⊥OM.若∠AOM=35°,则∠CON 的度数为( )
A.35°
B.45°
C.55°
D.65°
6
C
探索新知
2
知识点
垂线的画法
用三角尺画垂线的方法:
一贴,用三角尺的一条直角边贴住已知直线;
二靠,用三角尺的另一条直角边靠住已知点;
三画,画出垂线. 如果作线段互相垂直或作射线的垂
线,实际上是作线段所在的直线互相垂直,或作射线
所在的直线的垂线,因为射线和线段都是直线的一部
分.在垂线的画法中,有时需延长线段,垂足在延长
线上,并记上直角符号“﹁”.
探索新知
注意:画垂线也可用以下两种方法:
(1)利用量角器画;(2)用折叠法画.
探索新知
例3 如图,M 是三角形ABC 中BC 边上的任意一点,请
你按照下列要求画图:
(1)过M 点画直线AB 的垂线m;
(2)过M 点画直线BC 的垂线n;
(3)过M 点画直线AC 的垂线p.
探索新知
导引:观察图形不难看出,(1)(3)属于过直线外一点画
已知直线的垂线,(2)属于过直线上一点画已知
直线的垂线,所以按照“一靠、二过、三画”
的方法画图即可.
解:画出的直线m,n,p 如上页图.
探索新知
总 结
过已知点画已知直线的垂线,实际上就是过已知点画一条直线,使所画直线与已知直线相交所成的角是90°.
典题精讲
1
画一条线段或射线的垂线,就是画它们所在直线的垂线. 如图,请你过点P画出射线AB 或线段AB 的垂线.
如图所示.
解:
典题精讲
2
下列选项中,过点P 画AB 的垂线CD,三角板放法正确的是( ).
C
探索新知
3
知识点
垂线的性质
探究
如图.
(1)用三角尺或量角器画已知直线l 的垂线,这样的垂线能画出几条
(2)经过直线l 上一点A 画l 的垂线,这样的垂线能画出几条?
(3)经过直线l 外一点B 画l 的垂线,这样的垂线能画出几条?
探索新知
归 纳
经过一点(已知直线上或直线外),能画出已知直线的一条垂线,并且只 能画出一条垂线.即在同一平面内,过一点有且只有一条直线与已知直线垂直.
在平面内,不是在空间内,这是需要注意的条件:其中,一点可以是直线上一点也可以是直线外一点;“有且只有”中的“有”是指能画出一条已知直线的垂线,即存在性,“只有”是指只能画一条,即唯一性.
探索新知
例4 如图,已知直线AB,CB,l 在同一平面内,若AB⊥l,垂足为B,CB⊥l,垂足也为B,则符合题意的图形可以是( )
C
导引:根据题意可知,过点B 有AB,CB 都与直线l 垂直,由垂线的性质可知,在同一平面内,过一点有且只有一条直线与已知直线垂直,所以A、B、C 三点在一条直线上.
探索新知
总 结
利用直线的性质解答题目,要注意直线性质满足的条件:
1. 在平面内;
2. 过一点,点的位置可以在直线上也可以在直线外;
3. 相交所成的角必须是直角,以上三条缺一不可.
典题精讲
在同一平面内,下列语句正确的是( )
A.过一点有无数条直线与已知直线垂直
B.和一条直线垂直的直线有两条
C.过一点有且只有一条直线与已知直线垂直
D.若两直线相交,则它们一定垂直
1
C
易错提醒
(1)在图①中,过AB 外一点M 作AB 的垂线;
(2)在图②中,过点A,B分别作OB,OA 的垂线.
解:
(1)如图①所示.
(2)如图②所示.
易错点:误认为垂足一定要在线段或射线上而导致错误.
学以致用
小试牛刀
已知在同一平面内:
①两条直线相交成直角;
②两条直线互相垂直;
③一条直线是另一条直线的垂线.
那么下列因果关系:①→②③;②→①③;③→①②中,正确的有( )
A.0个 B.1个 C.2个 D.3个
D
1
典题精讲
过一条线段外一点,作这条线段的垂线,垂足在( )
A.这条线段上
B.这条线段的端点处
C.这条线段的延长线上
D.以上都有可能
D
2
小试牛刀
如图,如果直线ON⊥直线a,直线OM⊥直线a,那么OM 与ON 重合(即O,M,N 三点共线),其理由是( ).
A.两点确定一条直线
B.在同一平面内,过两点有且只有一条直线与已
知直线垂直
C.在同一平面内,过一点有且只有一条直线与已
知直线垂直
D.两点之间,线段最短
C
3
小试牛刀
4 在直线AB上任取一点O,过点O 作射线OC,OD,使OC⊥OD,当∠AOC=30°时,∠BOD 的度数是多少?
解:
如图①,当OC,OD 在直线AB 的同侧时,因为OC⊥OD,所以∠COD=90°.因为∠AOC=30°,所以∠BOD=180°-∠COD-∠AOC=60°.如图②,当OC,OD 在直线AB 的一侧时,因为OC⊥OD,所以∠COD=90°.因为∠AOC=30°,所以∠AOD=90°-∠AOC=60°.
所以∠BOD=180°-∠AOD=120°.
小试牛刀
5 已知OA⊥OB,OC⊥OD.
(1)如图①,若∠BOC=50°,求∠AOD 的度数;
(2)如图②,若∠BOC=60°,求∠AOD 的度数;
(3)根据(1)(2)的结果猜想∠AOD与∠BOC 有怎样的关系?并根据图①
说明理由;
(4)如图②,若∠BOC∶∠AOD=7∶29,求∠BOC 和∠AOD 的度数.
小试牛刀
解:
(1)因为OA⊥OB,所以∠AOB=90°,
所以∠AOC=∠AOB-∠BOC=90°-50°=40°.
因为OC⊥OD,所以∠COD=90°,
所以∠AOD=∠AOC+∠COD=40°+90°=130°.
(2)因为OA⊥OB,所以∠AOB=90°.
因为OC⊥OD,所以∠COD=90°,
所以∠AOD=360°-∠AOB-∠BOC-∠COD=
360°-90°-60°-90°=120°.
小试牛刀
(3)∠AOD 与∠BOC 互补.理由如下:
因为OA⊥OB,所以∠AOB=90°,
所以∠AOC=∠AOB-∠BOC=90°-∠BOC.
因为OC⊥OD,所以∠COD=90°,所以∠AOD=∠AOC
+∠COD=90°-∠BOC+90°=180°-∠BOC,所以
∠AOD+∠BOC=180°,即∠AOD 与∠BOC 互补.
(4)由(3)知∠BOC+∠AOD=180°,
又因为∠BOC∶∠AOD=7∶29,
所以∠BOC= ×180°=35°,
∠AOD= ×180°=145°.
小试牛刀
6 (1)在图①中以P为顶点作∠P,使∠P 的两边分别和∠1的两边垂直;
(2)量一量∠P 和∠1的度数,它们之间的数量关系是_________________;
解:
∠1+∠P=180°
(1)如图①所示.
课堂小结
课堂小结
以下几个方面由学生自己总结:
① 垂线的定义及垂直的符号表示;
② 垂线的有关性质;
③ 过一点作已知直线的垂线的方法.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
