【班海精品】人教版(新)七下-5.2 平行线及其判定 【优质教案】
文档属性
| 名称 | 【班海精品】人教版(新)七下-5.2 平行线及其判定 【优质教案】 |  | |
| 格式 | doc | ||
| 文件大小 | 374.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-09 17:35:23 | ||
图片预览




文档简介
班海数学精批——一本可精细批改的教辅
5.2 平行线及其判定 教案
平行线
【教学目标】
知识与技能:
感受平行线的概念,理解平行公理,能作出已知直线的平行线.
过程与方法:
通过观察、交流、探索等活动获取知识,在具体操作活动中了解平行线的有关性质.
情感态度与价值观:
丰富和发展自己的数学活动经历和体验,感受数学图形世界的丰富多彩.
【教学重难点】
重点:平行线的概念和平行公理.
难点:用几何语言描述作图过程.
【教学过程】
一、创设情境,引入新课
设计意图:创设多种有关平行的现实情境,激发学生的学习兴趣,让他们体会数学知识与现实生活的联系,掀起他们探究的欲望.
教师课件展示学生熟悉的有关平行线的现实情境,让学生观察:线、线与线的关系.如人行道、高压电线、百米跑道……
问题:这些线之间呈现怎样的位置关系
学生积极思考,观察后踊跃发言.
二、新知探索
设计意图:在让学生动手操作画平行线的过程中加深对平行线的理解,培养学生主动参与合作交流的意识,提高观察、分析、概括和抽象能力,培养学生的动手能力,引导学生探索平行线的性质.
1.教师板书课题,并说明本节课继续探讨现实生活中的平行现象,让学生给出平行的定义.一部分学生能回答出“不相交的两直线”而遗漏“在同一平面内”,教师此处应适当放开,让学生结合现实生活中的情景讨论“在同一平面内”的重要性.
教师出示问题:在教学中找平行线
学生讨论,组内交流,最后派代表发表见解.
师:生活中这么多平行,如何表示它们 如何画平行线
从而引出平行线的表示符号“∥”.
2.画平行线
教师让学生拿出方格纸,画出平行线,并进行组内交流.
总结画平行线的方法:一靠、二落、三推、四画.
为了让学生印象深刻,让学生板演,其余学生集中演示,体会.
3.平行线的性质
师:让学生拿出预制教具.(一块泡沫塑料上一根固定的木条和两根一端固定的木条)
问题:何种情形下,活动的木条与固定的木条平行
学生一边活动木条,一边思考,用自己的语言叙述:只有一种情形.
教师总结:经过直线外一点,有且只有一条直线与这条直线平行.进一步提问:若两根活动木条都与固定的木条平行,这两根活动木条有什么关系
学生经过讨论思考后,体会平行线的性质并积极发言.得出:如果两条直线都和第三条直线平行,那么这两条直线也互相平行.
三、巩固练习
设计意图:通过练习,巩固对平行线的认识,熟悉做已知直线的平行线的方法,达到学以致用的目的.
1.如图,四边形ABCD和四边形AFCE都是平行四边形,点E、F分别在CD、AB上,则图中平行线的组数是( )
A.2组 B.3组 C.4组 D.5组
2.如图,你能用学过的方法判断a、b这两条直线的位置关系吗
(1)过直线外一点A画直线l的平行线;
(2)找出图中所有的平行线,并用“∥”表示.
四、课堂小结
设计意图:由练习过渡到小结中,让学生再次体会,知识来自于实践中,反过来又指导实践,初步体验知识的系统性和完整性.
小结:本课你从现实情境中了解了什么知识 对你获取的信息说说你的反思.
五、课后作业
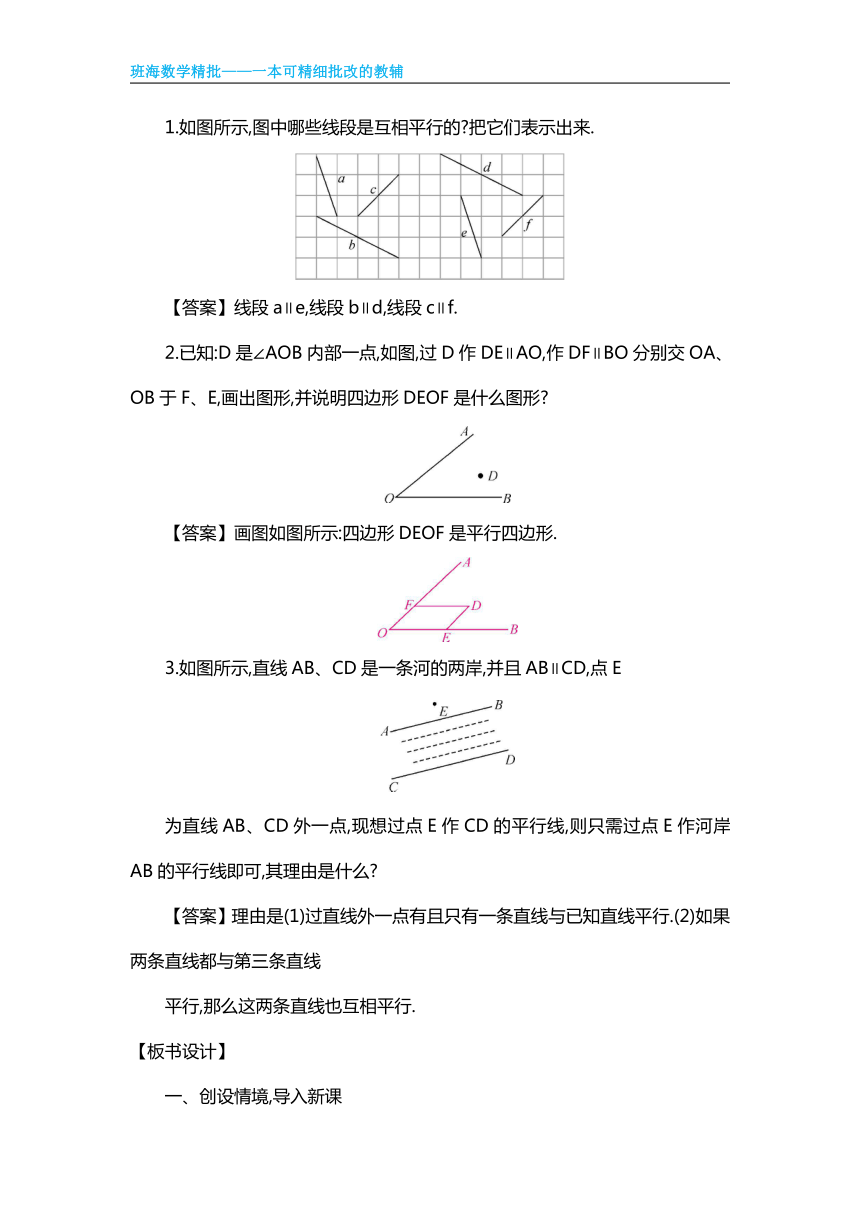
1.如图所示,图中哪些线段是互相平行的 把它们表示出来.
【答案】线段a∥e,线段b∥d,线段c∥f.
2.已知:D是∠AOB内部一点,如图,过D作DE∥AO,作DF∥BO分别交OA、OB于F、E,画出图形,并说明四边形DEOF是什么图形
【答案】画图如图所示:四边形DEOF是平行四边形.
3.如图所示,直线AB、CD是一条河的两岸,并且AB∥CD,点E
为直线AB、CD外一点,现想过点E作CD的平行线,则只需过点E作河岸AB的平行线即可,其理由是什么
【答案】理由是(1)过直线外一点有且只有一条直线与已知直线平行.(2)如果两条直线都与第三条直线
平行,那么这两条直线也互相平行.
【板书设计】
一、创设情境,导入新课
二、新知探索
三、巩固练习
四、课堂小结
五、课后作业
平行线的判定——利用“同位角、第三直线”
教学目标:经历探索两直线平行条件的过程,理解两直线平行的条件.
重点:探索两直线平行的条件
难点:理解“同位角相等,两条直线平行”
教学过程
一、情景导入.
装修工人正在向墙上钉木条,如果木条b与墙壁边缘垂直,那么木条a与墙壁边缘所夹角为多少度时,才能使木条a与木条b平行?
要解决这个问题,就要弄清楚平行的判定。
二、直线平行的条件
以前我们学过用直尺和三角尺画平行线,如图(课本P13图5.2-5)在三角板移动的过程中,什么没有变?
三角板经过点P的边与靠在直尺上的边所成的角没有变。
简化图5.2-5,得图3.
∠1与∠2是三角板经过点P的边与靠在直尺上的边所成的角移动前后的位置,显然∠1与∠2是同位角并且它们相等,由此我们可以知道什么?
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单地说:同位角相等,两条直线平行.
符号语言:∵∠1=∠2∴AB∥CD.
如图(课本P145.2-7),你能说出木工用图中这种叫做角尺的工具画平行线的道理吗?
用角尺画平行线,实际上是画出了两个直角,根据“同位角相等,两条直线平行.”,可知这样画出的就是平行线。
如图,(1)如果∠2=∠3,能得出a∥b吗?(2)如果∠2+∠4=1800,能得出a∥b吗?
你能用文字语言概括上面的结论吗?
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单地说:内错角相等,两直线平行.
符号语言:∵∠2=∠3∴a∥b.
(2)∵∠4+∠2=180°,∠4+∠1=180°(已知)
∴∠2=∠1(同角的补角相等)
∴a∥b.(同位角相等,两条直线平行)
你能用文字语言概括上面的结论吗?
两条直线被第三条直线所截,如果同旁内角互补,那么两条直线平行.
简单地说:同旁内角互补,两直线平行.
符号语言:∵∠4+∠2=180°∴a∥b.
四、课堂练习
1、课本P15练习1,补充(3)由∠A+∠ABC=1800可以判断哪两条直线平行?依据是什么?
2、课本P16
五、课堂小结:怎样判断两条直线平行?
六、布置作业::P16、1、2题;P174、5、6。
平行线的判定--利用“内错角、同旁内角”
【教学目标】
知识与技能:
使学生认识平行线的识别法,能灵活地利用平行线的两个识别法解决一些简单的问题.
过程与方法:
经历平行线两种识别方法的发现过程,让学生通过直观感知,操作确认等实践活动,加强对图形的认识和感受.
情感态度与价值观:
通过实地观测建筑物,让学生体会数学之美,对学生进行美学教育,渗透数学源于实践又作用于实践的辩证唯物主义观点.
【教学重难点】
重点:平行线的两种识别方法.
难点:运用两种识别方法进行简单的推理.
【教学过程】
一、提出问题,创设情境
设计意图:通过巧妙的设置问题,引导学生思考,既复习旧知识,做好新知识学习的铺垫,也不断激活学生思维,生成新问题,引起认知冲突,从而自然引入新课.
1.复习提问:什么叫平行线
引导学生注意在同一平面内这一条件.
2.教师出示多媒体(图形显示,教师口述内容)
在现实生活中,有不少平行的例子.例如:我们学校建筑物上就有平行线,上图是我们学校的校道对应的几何图形,我们已分组测量了α、β的度数,请几个小组同学说说测量的结果,老师告诉你:根据α=β,可得出校道中两段笔直的部分是平行的,想知道为什么吗 带着这个问题,我们来学行线的识别”.(板书课题)
二、动手实验,发现新知
设计意图:在实现教学活动的过程中,使实际问题与学生生活密切联系,学生有较好的参与意识和学习兴趣,随着教师问题的提出而不断进行更深入的思考,设计的动手实验以教材为基础,实现了让学生通过动手操作,在变化中感受角的大小变化与直线位置关系的联系,实现了由感性到理性的上升.
两条直线被第三条直线所截,如果同位角相等,那么这两直线平行.(同位角相等,两直线平行)
例如:如图,直线a、b被直线l所截,如果∠1=∠3,那么a∥b.
(交流后得出)
因为∠1=∠3(已知),∠2=∠3(对顶角相等),所以∠1=∠2,
∴a∥b.(同位角相等,两直线平行)
结论:内错角相等,两直线平行.
三、运用新知
设计意图:及时训练是巩固知识的必要手段,练习题的选择要为教学目标的实现服务,通过学生的练习,通过巩固了上面得出的平行线的两种识别法;又在学生的自主探究中,得出平行线的第三种识别方法,实现了在练中学,在学中练的统一.
教师出示
如图,直线a、b被直线l所截,已知∠1=115°,∠2=115°,那么a∥b吗 为什么
学生思考后根据所学知识做出解答.
变式训练:若在以上问题中,∠1=115°,∠3=65°,那么a∥b吗 为什么
学生交流,讨论得出:同旁内角互补,两直线平行.
如图,在四边形ABCD中,已知∠B=60°,∠C=120°,AB与CD平行吗 AD与BC平行吗
教师让学生先独立思考,然后再交流,完成对以上题目的解答.注意引导学生的推理过程,步骤的逻辑性.
四、课堂小结
设计意图:学生在一节课积极、热烈的探究、合作学习之余,需要有一点时间静下心来默默地反思自己,这是对知识沉淀、吸收的过程,通过生生、师生的交流,形成完整的知识结构.
师:平行线识别的几种方法是什么
通过今天的学习,你想进一步探究的问题是什么
五、课后作业
1.如图,∠1=∠2,∠3=∠4,试问EF是否与GH
平行
【答案】因为∠1=∠2(已知),又因为∠CGE=∠2(对顶角相等),所以∠1=∠CGE(等量代换),又因为∠3=∠4(已知),所以∠3+∠1=∠4+∠CGE,
即∠MEF=∠EGH,所以EF∥GH(同位角相等,两直线平行).
2.如图,已知∠1=35°,∠B=55°,AB⊥AC,则
(1)∠DAB+∠B= ;(2)AD与BC平行吗 AB与CD平行吗 若平行,请说明理由;若不一定,那么再加上什么条件就平行了呢
【答案】(1)180° (2)AD∥BC,理由:同旁内角互补,两条直线平行;AB与CD不一定平行,若要使AB∥CD,则须满足AC⊥DC,或∠B+∠BCD=180°.
【板书设计】
一、提出问题,创设情境
二、动手实验,发现新知
三、运用新知
四、课堂小结
五、课后作业
感谢您下载使用【班海】教学资源。班海——老师们都在免费用的数学作业精细批改微信小程序!
3
2
b
a
c
4
1
(1)∵∠2=∠3(已知)∠3=∠1(对顶角相等)
∴∠1=∠2(等量代换)
∴a∥b(同位角相等,两条直线平行)
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
5.2 平行线及其判定 教案
平行线
【教学目标】
知识与技能:
感受平行线的概念,理解平行公理,能作出已知直线的平行线.
过程与方法:
通过观察、交流、探索等活动获取知识,在具体操作活动中了解平行线的有关性质.
情感态度与价值观:
丰富和发展自己的数学活动经历和体验,感受数学图形世界的丰富多彩.
【教学重难点】
重点:平行线的概念和平行公理.
难点:用几何语言描述作图过程.
【教学过程】
一、创设情境,引入新课
设计意图:创设多种有关平行的现实情境,激发学生的学习兴趣,让他们体会数学知识与现实生活的联系,掀起他们探究的欲望.
教师课件展示学生熟悉的有关平行线的现实情境,让学生观察:线、线与线的关系.如人行道、高压电线、百米跑道……
问题:这些线之间呈现怎样的位置关系
学生积极思考,观察后踊跃发言.
二、新知探索
设计意图:在让学生动手操作画平行线的过程中加深对平行线的理解,培养学生主动参与合作交流的意识,提高观察、分析、概括和抽象能力,培养学生的动手能力,引导学生探索平行线的性质.
1.教师板书课题,并说明本节课继续探讨现实生活中的平行现象,让学生给出平行的定义.一部分学生能回答出“不相交的两直线”而遗漏“在同一平面内”,教师此处应适当放开,让学生结合现实生活中的情景讨论“在同一平面内”的重要性.
教师出示问题:在教学中找平行线
学生讨论,组内交流,最后派代表发表见解.
师:生活中这么多平行,如何表示它们 如何画平行线
从而引出平行线的表示符号“∥”.
2.画平行线
教师让学生拿出方格纸,画出平行线,并进行组内交流.
总结画平行线的方法:一靠、二落、三推、四画.
为了让学生印象深刻,让学生板演,其余学生集中演示,体会.
3.平行线的性质
师:让学生拿出预制教具.(一块泡沫塑料上一根固定的木条和两根一端固定的木条)
问题:何种情形下,活动的木条与固定的木条平行
学生一边活动木条,一边思考,用自己的语言叙述:只有一种情形.
教师总结:经过直线外一点,有且只有一条直线与这条直线平行.进一步提问:若两根活动木条都与固定的木条平行,这两根活动木条有什么关系
学生经过讨论思考后,体会平行线的性质并积极发言.得出:如果两条直线都和第三条直线平行,那么这两条直线也互相平行.
三、巩固练习
设计意图:通过练习,巩固对平行线的认识,熟悉做已知直线的平行线的方法,达到学以致用的目的.
1.如图,四边形ABCD和四边形AFCE都是平行四边形,点E、F分别在CD、AB上,则图中平行线的组数是( )
A.2组 B.3组 C.4组 D.5组
2.如图,你能用学过的方法判断a、b这两条直线的位置关系吗
(1)过直线外一点A画直线l的平行线;
(2)找出图中所有的平行线,并用“∥”表示.
四、课堂小结
设计意图:由练习过渡到小结中,让学生再次体会,知识来自于实践中,反过来又指导实践,初步体验知识的系统性和完整性.
小结:本课你从现实情境中了解了什么知识 对你获取的信息说说你的反思.
五、课后作业
1.如图所示,图中哪些线段是互相平行的 把它们表示出来.
【答案】线段a∥e,线段b∥d,线段c∥f.
2.已知:D是∠AOB内部一点,如图,过D作DE∥AO,作DF∥BO分别交OA、OB于F、E,画出图形,并说明四边形DEOF是什么图形
【答案】画图如图所示:四边形DEOF是平行四边形.
3.如图所示,直线AB、CD是一条河的两岸,并且AB∥CD,点E
为直线AB、CD外一点,现想过点E作CD的平行线,则只需过点E作河岸AB的平行线即可,其理由是什么
【答案】理由是(1)过直线外一点有且只有一条直线与已知直线平行.(2)如果两条直线都与第三条直线
平行,那么这两条直线也互相平行.
【板书设计】
一、创设情境,导入新课
二、新知探索
三、巩固练习
四、课堂小结
五、课后作业
平行线的判定——利用“同位角、第三直线”
教学目标:经历探索两直线平行条件的过程,理解两直线平行的条件.
重点:探索两直线平行的条件
难点:理解“同位角相等,两条直线平行”
教学过程
一、情景导入.
装修工人正在向墙上钉木条,如果木条b与墙壁边缘垂直,那么木条a与墙壁边缘所夹角为多少度时,才能使木条a与木条b平行?
要解决这个问题,就要弄清楚平行的判定。
二、直线平行的条件
以前我们学过用直尺和三角尺画平行线,如图(课本P13图5.2-5)在三角板移动的过程中,什么没有变?
三角板经过点P的边与靠在直尺上的边所成的角没有变。
简化图5.2-5,得图3.
∠1与∠2是三角板经过点P的边与靠在直尺上的边所成的角移动前后的位置,显然∠1与∠2是同位角并且它们相等,由此我们可以知道什么?
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单地说:同位角相等,两条直线平行.
符号语言:∵∠1=∠2∴AB∥CD.
如图(课本P145.2-7),你能说出木工用图中这种叫做角尺的工具画平行线的道理吗?
用角尺画平行线,实际上是画出了两个直角,根据“同位角相等,两条直线平行.”,可知这样画出的就是平行线。
如图,(1)如果∠2=∠3,能得出a∥b吗?(2)如果∠2+∠4=1800,能得出a∥b吗?
你能用文字语言概括上面的结论吗?
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单地说:内错角相等,两直线平行.
符号语言:∵∠2=∠3∴a∥b.
(2)∵∠4+∠2=180°,∠4+∠1=180°(已知)
∴∠2=∠1(同角的补角相等)
∴a∥b.(同位角相等,两条直线平行)
你能用文字语言概括上面的结论吗?
两条直线被第三条直线所截,如果同旁内角互补,那么两条直线平行.
简单地说:同旁内角互补,两直线平行.
符号语言:∵∠4+∠2=180°∴a∥b.
四、课堂练习
1、课本P15练习1,补充(3)由∠A+∠ABC=1800可以判断哪两条直线平行?依据是什么?
2、课本P16
五、课堂小结:怎样判断两条直线平行?
六、布置作业::P16、1、2题;P174、5、6。
平行线的判定--利用“内错角、同旁内角”
【教学目标】
知识与技能:
使学生认识平行线的识别法,能灵活地利用平行线的两个识别法解决一些简单的问题.
过程与方法:
经历平行线两种识别方法的发现过程,让学生通过直观感知,操作确认等实践活动,加强对图形的认识和感受.
情感态度与价值观:
通过实地观测建筑物,让学生体会数学之美,对学生进行美学教育,渗透数学源于实践又作用于实践的辩证唯物主义观点.
【教学重难点】
重点:平行线的两种识别方法.
难点:运用两种识别方法进行简单的推理.
【教学过程】
一、提出问题,创设情境
设计意图:通过巧妙的设置问题,引导学生思考,既复习旧知识,做好新知识学习的铺垫,也不断激活学生思维,生成新问题,引起认知冲突,从而自然引入新课.
1.复习提问:什么叫平行线
引导学生注意在同一平面内这一条件.
2.教师出示多媒体(图形显示,教师口述内容)
在现实生活中,有不少平行的例子.例如:我们学校建筑物上就有平行线,上图是我们学校的校道对应的几何图形,我们已分组测量了α、β的度数,请几个小组同学说说测量的结果,老师告诉你:根据α=β,可得出校道中两段笔直的部分是平行的,想知道为什么吗 带着这个问题,我们来学行线的识别”.(板书课题)
二、动手实验,发现新知
设计意图:在实现教学活动的过程中,使实际问题与学生生活密切联系,学生有较好的参与意识和学习兴趣,随着教师问题的提出而不断进行更深入的思考,设计的动手实验以教材为基础,实现了让学生通过动手操作,在变化中感受角的大小变化与直线位置关系的联系,实现了由感性到理性的上升.
两条直线被第三条直线所截,如果同位角相等,那么这两直线平行.(同位角相等,两直线平行)
例如:如图,直线a、b被直线l所截,如果∠1=∠3,那么a∥b.
(交流后得出)
因为∠1=∠3(已知),∠2=∠3(对顶角相等),所以∠1=∠2,
∴a∥b.(同位角相等,两直线平行)
结论:内错角相等,两直线平行.
三、运用新知
设计意图:及时训练是巩固知识的必要手段,练习题的选择要为教学目标的实现服务,通过学生的练习,通过巩固了上面得出的平行线的两种识别法;又在学生的自主探究中,得出平行线的第三种识别方法,实现了在练中学,在学中练的统一.
教师出示
如图,直线a、b被直线l所截,已知∠1=115°,∠2=115°,那么a∥b吗 为什么
学生思考后根据所学知识做出解答.
变式训练:若在以上问题中,∠1=115°,∠3=65°,那么a∥b吗 为什么
学生交流,讨论得出:同旁内角互补,两直线平行.
如图,在四边形ABCD中,已知∠B=60°,∠C=120°,AB与CD平行吗 AD与BC平行吗
教师让学生先独立思考,然后再交流,完成对以上题目的解答.注意引导学生的推理过程,步骤的逻辑性.
四、课堂小结
设计意图:学生在一节课积极、热烈的探究、合作学习之余,需要有一点时间静下心来默默地反思自己,这是对知识沉淀、吸收的过程,通过生生、师生的交流,形成完整的知识结构.
师:平行线识别的几种方法是什么
通过今天的学习,你想进一步探究的问题是什么
五、课后作业
1.如图,∠1=∠2,∠3=∠4,试问EF是否与GH
平行
【答案】因为∠1=∠2(已知),又因为∠CGE=∠2(对顶角相等),所以∠1=∠CGE(等量代换),又因为∠3=∠4(已知),所以∠3+∠1=∠4+∠CGE,
即∠MEF=∠EGH,所以EF∥GH(同位角相等,两直线平行).
2.如图,已知∠1=35°,∠B=55°,AB⊥AC,则
(1)∠DAB+∠B= ;(2)AD与BC平行吗 AB与CD平行吗 若平行,请说明理由;若不一定,那么再加上什么条件就平行了呢
【答案】(1)180° (2)AD∥BC,理由:同旁内角互补,两条直线平行;AB与CD不一定平行,若要使AB∥CD,则须满足AC⊥DC,或∠B+∠BCD=180°.
【板书设计】
一、提出问题,创设情境
二、动手实验,发现新知
三、运用新知
四、课堂小结
五、课后作业
感谢您下载使用【班海】教学资源。班海——老师们都在免费用的数学作业精细批改微信小程序!
3
2
b
a
c
4
1
(1)∵∠2=∠3(已知)∠3=∠1(对顶角相等)
∴∠1=∠2(等量代换)
∴a∥b(同位角相等,两条直线平行)
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
