【班海精品】人教版(新)七下-5.1 相交线 第一课时【优质课件】
文档属性
| 名称 | 【班海精品】人教版(新)七下-5.1 相交线 第一课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 8.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-09 17:35:23 | ||
图片预览






文档简介
(共41张PPT)
5.1 相交线
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
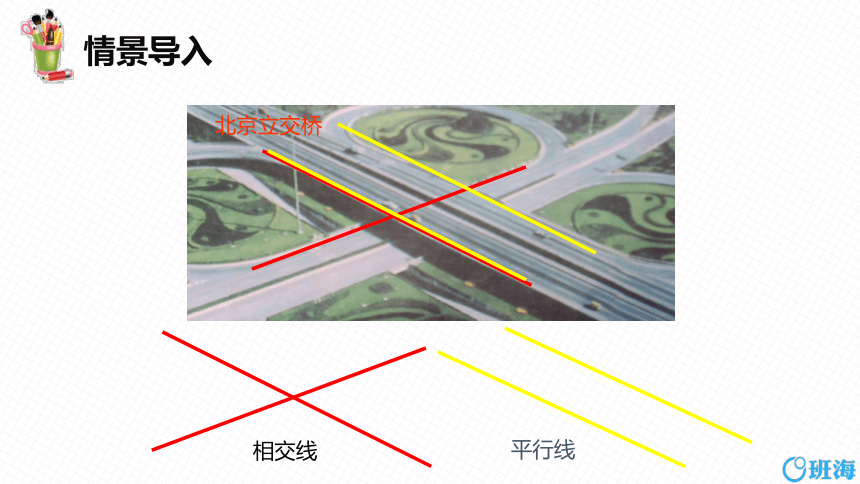
情景导入
北京立交桥
相交线
平行线
新课精讲
探索新知
1
知识点
邻补角及其性质
A
B
C
D
O
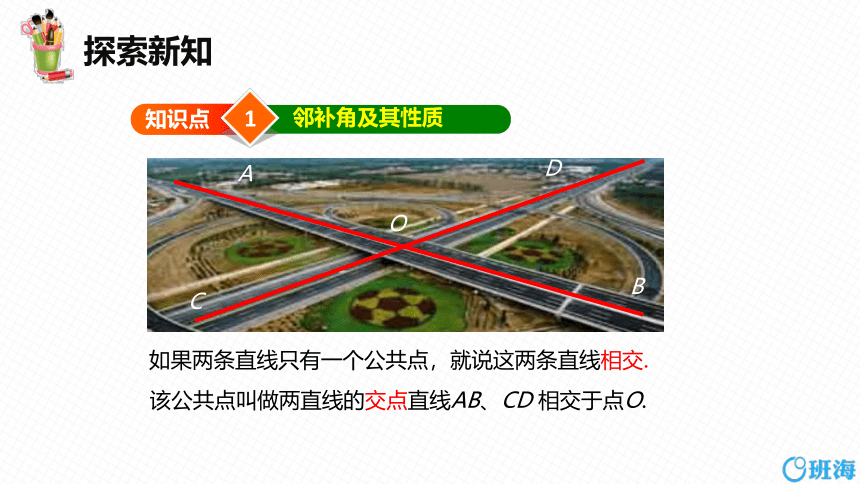
如果两条直线只有一个公共点,就说这两条直线相交.
该公共点叫做两直线的交点直线AB、CD 相交于点O.
探索新知
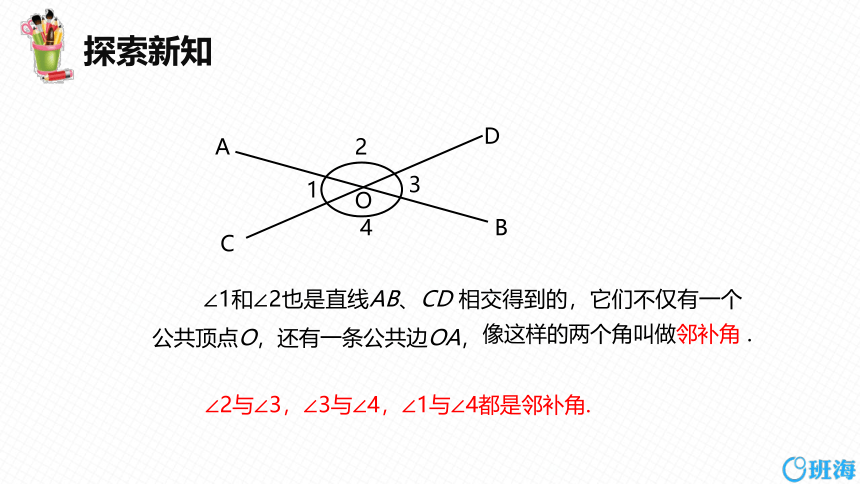
∠1和∠2也是直线AB、CD 相交得到的,它们不仅有一个公共顶点O,还有一条公共边OA,
像这样的两个角叫做邻补角 .
∠2与∠3,∠3与∠4,∠1与∠4都是邻补角.
A
B
C
D
O
1
2
3
4
探索新知
1
2
A
C
D
O
3
4
B
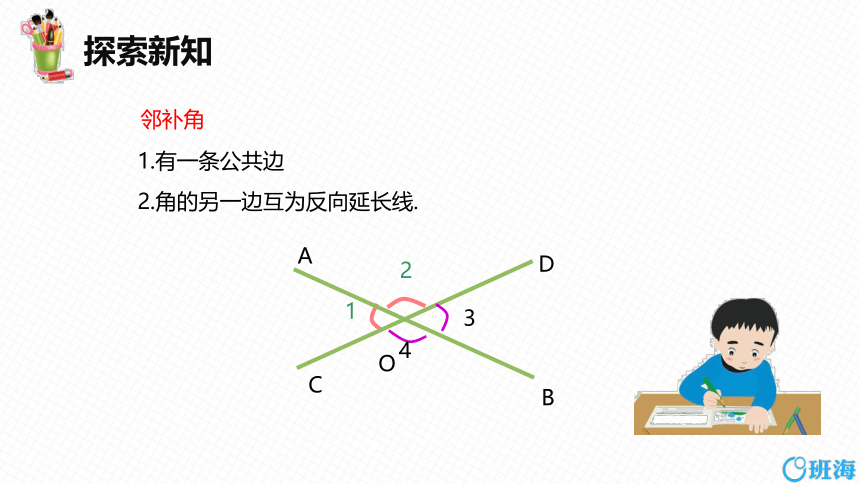
1.有一条公共边
2.角的另一边互为反向延长线.
邻补角
探索新知
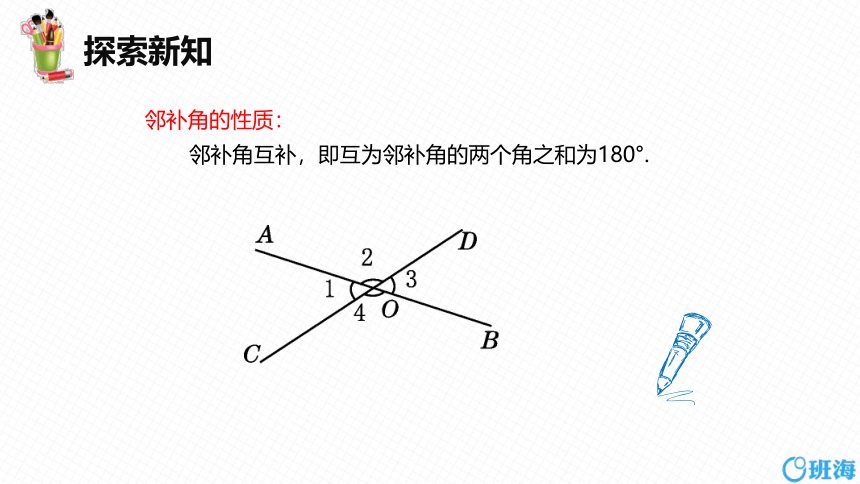
邻补角的性质:
邻补角互补,即互为邻补角的两个角之和为180°.
探索新知
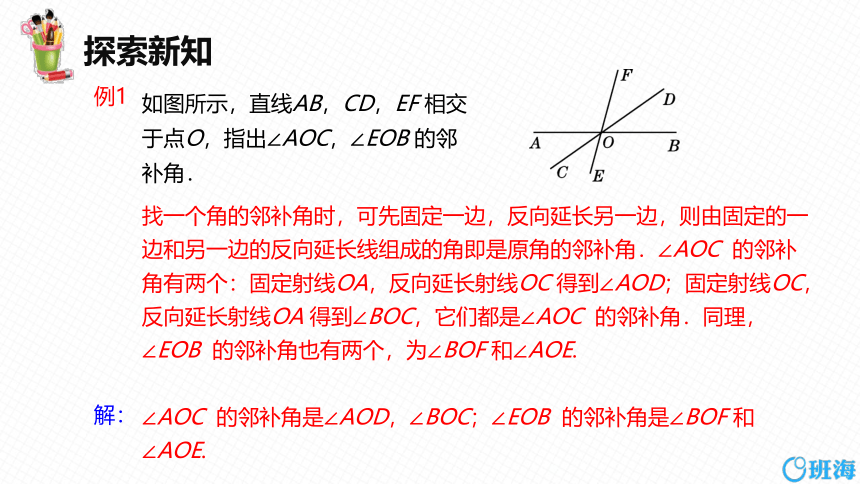
如图所示,直线AB,CD,EF 相交于点O,指出∠AOC,∠EOB 的邻补角.
例1
找一个角的邻补角时,可先固定一边,反向延长另一边,则由固定的一边和另一边的反向延长线组成的角即是原角的邻补角.∠AOC 的邻补角有两个:固定射线OA,反向延长射线OC 得到∠AOD;固定射线OC,反向延长射线OA 得到∠BOC,它们都是∠AOC 的邻补角.同理,∠EOB 的邻补角也有两个,为∠BOF 和∠AOE.
∠AOC 的邻补角是∠AOD,∠BOC;∠EOB 的邻补角是∠BOF 和∠AOE.
解:
探索新知
总 结
判断两个角是不是邻补角,应从两个方面去看:
一看这两个角有没有公共边;
二看这两个角的另一边是否互为反向延长线.
典题精讲
1 邻补角是( )
A.和为180°的两个角
B.有公共顶点且互补的两个角
C.有一条公共边且相等的两个角
D.有公共顶点且有一条公共边,另一边互为反向延长线
的两个角
D
典题精讲
2 下列选项中,∠1与∠2互为邻补角的是( )
D
典题精讲
3 如图,∠1的邻补角是( )
A.∠BOC
B.∠BOE 和∠AOF
C.∠AOF
D.∠BOC 和∠AOF
B
典题精讲
4 如图,∠α的度数等于( )
A.135°
B.125°
C.115°
D.105°
A
探索新知
2
知识点
对顶角及其性质
O
A
B
C
D
)
(
1
3
4
2
)
(
有一个公共顶点一个角的两边是另一个角的两边的反向延长线,那么这两个角互为对顶角.
对顶角:
探索新知
对顶角
1.顶点相同.
2.角的两边互为反向延长线.
B
A
O
C
D
1
2
两条直线相交出现对顶角
对顶角是成对出现的
探索新知
如图,∠1与∠2是对顶角的是( )
例2
判断两个角是不是对顶角,要紧扣对顶角的定义,A图中∠1和∠2的顶点不同;B图中∠1和∠2的两边都不是互为反向延长线;C图中的∠1和∠2符合定义;D图中∠1和∠2有一条公共边.
C
探索新知
总 结
判断两个角是否互为对顶角的方法:
一看它们有没有公共顶点;
二看这两个角的两边是否互为反向延长线,实质就是看这两个角是否是两条直线相交所成的没有公共边的两个角.
探索新知
如图,直线a, b 相交,∠1 = 40°, 求∠2,∠3,∠4的度数.
由邻补角的定义,得
∠2 = 180°-∠1
= 180°-40°=140°;
由对顶角相等,得
∠3= ∠1=40° ,
∠4= ∠2 = 140°.
例3
解:
探索新知
总 结
对顶角和邻补角经常在求角的度数的题目中同时用到,只要分清楚对顶角、邻补角的性质,就是对顶角相等、邻补角互补,此类题目容易解答.
典题精讲
如图,取两根木条a,b,将它们钉在一起,并把它们想象成两条直线,就得到一个相交线的模型.你能说出其中的一些邻补角与对顶角吗?两根木条所成的角中,如果∠α=35°,其他三 个角各等于多少度?如果∠α 等于90°,115°,m°呢?
典题精讲
说出邻补角与对顶角略.如果其中一个角是35°,那么其他三个角分别是145°,35°,145°;如果这个角是90°,那么其他三个角都是90°;如果这个角是115°,那么其他三个角分别是65°,115°,65°;如果这个角是m°,那么其他三个角分别是180°-m°,m°,180°-m°.
解:
典题精讲
如图,小强和小丽一起玩跷跷板,横板AB 绕O上下转动,当小强从A到A′的位置时,∠AOA′=45°,则∠BOB ′ 的度数为________,理由是__________________.
45°
对顶角相等
典题精讲
3 如图,直线AB,CD 交于点O,下列说法中,错误的是( )
A.∠AOC 与∠BOD 是对顶角
B.∠AOE 与∠BOE 是邻补角
C.∠DOE 与∠BOC 是对顶角
D.∠AOD 与∠BOC 都是∠AOC 的邻补角
C
典题精讲
4
下面四个图形中,∠1=∠2一定成立的是( )
B
典题精讲
5
如图,三条直线交于点O,则∠1+∠2+∠3等于( )
A.90°
B.120°
C.180°
D.360°
C
易错提醒
如图,点O 是直线AB上的任意一点,OC,OD,OE是过点O 的三条射线,若∠AOD=∠COE=90°,则下列说法:①与∠AOC 互为邻补角的角只有一个;②与∠AOC 互为补角的角只有一个;③与∠AOC 互为邻补角的角有两个;④与∠AOC 互为补角的角有两个.其中正确的是( )
A.②③ B.①②
C.③④ D.①④
D
学以致用
小试牛刀
1 如图,直线AB,CD 相交于点O,OE 平分∠AOD,若∠DOE=36°,则∠BOC 的度数为( )
A.72°
B.90°
C.108°
D.144°
A
小试牛刀
2 如图,直线AB、CD、EF 相交于点O.
(1)写出∠COE 的邻补角;
(2)分别写出∠COE 和∠BOE 的对顶角;
(3)如果∠BOD=60°,∠BOF=90°,求∠AOF 和
∠FOC 的度数.
小试牛刀
(1)∠COE 的邻补角为∠COF 和∠EOD.
(2)∠COE 和∠BOE 的对顶角分别为∠DOF 和∠AOF.
(3)因为∠BOF=90°,
所以∠AOF=90°.
又因为∠AOC=∠BOD=60°,
所以∠FOC=∠AOF+∠AOC=90°+60°=150°.
解:
小试牛刀
3 将一张长方形纸片按图中的方式折叠,BC,BD为折痕,求∠CBD 的大小.
解:
由折叠的性质可知∠ABC=∠A′BC,
∠EBD=∠E ′BD,所以∠A′BC= ∠ABE ′,
∠E ′BD= ∠EBE ′.由∠ABE ′与∠EBE ′互为邻补角,
得∠ABE ′+∠EBE ′=180°,所以∠CBD=∠A′BC+∠E ′BD= ∠ABE ′+ ∠EBE ′= (∠ABE ′+∠EBE ′)=90°.
小试牛刀
4 如图所示,直线AB,CD 交于点O,OE 平分∠AOD,OF 平分∠DOB.
(1)若∠AOC=60°,求∠DOF 与∠DOE 的度数,并计算∠EOF 的度数;
(2)当∠AOC 的度数变化时,∠EOF 的度数是否变化?
说明理由.
小试牛刀
解:
(1)由邻补角的定义,
得∠AOD=180°-∠AOC=180°-60°=120°.
由对顶角相等,得∠BOD=∠AOC=60°.
因为OF 平分∠BOD,所以∠DOF= ∠BOD=30°.
同理∠DOE= ∠AOD=60°,
所以∠EOF=∠DOF+∠DOE=90°.
小试牛刀
(2)∠EOF 的度数不发生变化.理由如下:
因为OF 平分∠BOD,所以∠DOF= ∠BOD.
同理∠DOE= ∠AOD.
因为∠BOD+∠AOD=180°,
所以∠EOF=∠DOF+∠DOE= (∠BOD+∠AOD )=90°.
小试牛刀
5 观察下列各图,寻找对顶角(不含平角)、邻补角.
(1)如图①,图中共有________对对顶角,________对邻补角;
(2)如图②,图中共有________对对顶角,________对邻补角;
(3)如图③,图中共有________对对顶角,________对邻补角;
2
4
6
12
12
24
小试牛刀
(4)研究(1)~(3)小题中直线条数与对顶角、邻补角的对数
之间的关系,若有n 条直线相交于一点,则有多少对对
顶角,多少对邻补角?
有n(n-1)对对顶角,2n(n-1)对邻补角.
解:
课堂小结
角的名称 特征 性质 相同点 不同点
对顶角 ①两条直线相交面成的角 ②有一个公共顶点 ③没有公共边 对顶角相等 都是两直线相交而成的角,都有一个公共顶点,它们都是成对出现. 对顶角没有公共边而邻补角有一条公共边;两条直线相交时,一个有的对顶角有一个,而一个角的邻补角有两个.
邻补角 ①两条直线相交面成的角②有一个公共顶点 ③有一条公共边 邻补角互补 课堂小结
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
5.1 相交线
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
北京立交桥
相交线
平行线
新课精讲
探索新知
1
知识点
邻补角及其性质
A
B
C
D
O
如果两条直线只有一个公共点,就说这两条直线相交.
该公共点叫做两直线的交点直线AB、CD 相交于点O.
探索新知
∠1和∠2也是直线AB、CD 相交得到的,它们不仅有一个公共顶点O,还有一条公共边OA,
像这样的两个角叫做邻补角 .
∠2与∠3,∠3与∠4,∠1与∠4都是邻补角.
A
B
C
D
O
1
2
3
4
探索新知
1
2
A
C
D
O
3
4
B
1.有一条公共边
2.角的另一边互为反向延长线.
邻补角
探索新知
邻补角的性质:
邻补角互补,即互为邻补角的两个角之和为180°.
探索新知
如图所示,直线AB,CD,EF 相交于点O,指出∠AOC,∠EOB 的邻补角.
例1
找一个角的邻补角时,可先固定一边,反向延长另一边,则由固定的一边和另一边的反向延长线组成的角即是原角的邻补角.∠AOC 的邻补角有两个:固定射线OA,反向延长射线OC 得到∠AOD;固定射线OC,反向延长射线OA 得到∠BOC,它们都是∠AOC 的邻补角.同理,∠EOB 的邻补角也有两个,为∠BOF 和∠AOE.
∠AOC 的邻补角是∠AOD,∠BOC;∠EOB 的邻补角是∠BOF 和∠AOE.
解:
探索新知
总 结
判断两个角是不是邻补角,应从两个方面去看:
一看这两个角有没有公共边;
二看这两个角的另一边是否互为反向延长线.
典题精讲
1 邻补角是( )
A.和为180°的两个角
B.有公共顶点且互补的两个角
C.有一条公共边且相等的两个角
D.有公共顶点且有一条公共边,另一边互为反向延长线
的两个角
D
典题精讲
2 下列选项中,∠1与∠2互为邻补角的是( )
D
典题精讲
3 如图,∠1的邻补角是( )
A.∠BOC
B.∠BOE 和∠AOF
C.∠AOF
D.∠BOC 和∠AOF
B
典题精讲
4 如图,∠α的度数等于( )
A.135°
B.125°
C.115°
D.105°
A
探索新知
2
知识点
对顶角及其性质
O
A
B
C
D
)
(
1
3
4
2
)
(
有一个公共顶点一个角的两边是另一个角的两边的反向延长线,那么这两个角互为对顶角.
对顶角:
探索新知
对顶角
1.顶点相同.
2.角的两边互为反向延长线.
B
A
O
C
D
1
2
两条直线相交出现对顶角
对顶角是成对出现的
探索新知
如图,∠1与∠2是对顶角的是( )
例2
判断两个角是不是对顶角,要紧扣对顶角的定义,A图中∠1和∠2的顶点不同;B图中∠1和∠2的两边都不是互为反向延长线;C图中的∠1和∠2符合定义;D图中∠1和∠2有一条公共边.
C
探索新知
总 结
判断两个角是否互为对顶角的方法:
一看它们有没有公共顶点;
二看这两个角的两边是否互为反向延长线,实质就是看这两个角是否是两条直线相交所成的没有公共边的两个角.
探索新知
如图,直线a, b 相交,∠1 = 40°, 求∠2,∠3,∠4的度数.
由邻补角的定义,得
∠2 = 180°-∠1
= 180°-40°=140°;
由对顶角相等,得
∠3= ∠1=40° ,
∠4= ∠2 = 140°.
例3
解:
探索新知
总 结
对顶角和邻补角经常在求角的度数的题目中同时用到,只要分清楚对顶角、邻补角的性质,就是对顶角相等、邻补角互补,此类题目容易解答.
典题精讲
如图,取两根木条a,b,将它们钉在一起,并把它们想象成两条直线,就得到一个相交线的模型.你能说出其中的一些邻补角与对顶角吗?两根木条所成的角中,如果∠α=35°,其他三 个角各等于多少度?如果∠α 等于90°,115°,m°呢?
典题精讲
说出邻补角与对顶角略.如果其中一个角是35°,那么其他三个角分别是145°,35°,145°;如果这个角是90°,那么其他三个角都是90°;如果这个角是115°,那么其他三个角分别是65°,115°,65°;如果这个角是m°,那么其他三个角分别是180°-m°,m°,180°-m°.
解:
典题精讲
如图,小强和小丽一起玩跷跷板,横板AB 绕O上下转动,当小强从A到A′的位置时,∠AOA′=45°,则∠BOB ′ 的度数为________,理由是__________________.
45°
对顶角相等
典题精讲
3 如图,直线AB,CD 交于点O,下列说法中,错误的是( )
A.∠AOC 与∠BOD 是对顶角
B.∠AOE 与∠BOE 是邻补角
C.∠DOE 与∠BOC 是对顶角
D.∠AOD 与∠BOC 都是∠AOC 的邻补角
C
典题精讲
4
下面四个图形中,∠1=∠2一定成立的是( )
B
典题精讲
5
如图,三条直线交于点O,则∠1+∠2+∠3等于( )
A.90°
B.120°
C.180°
D.360°
C
易错提醒
如图,点O 是直线AB上的任意一点,OC,OD,OE是过点O 的三条射线,若∠AOD=∠COE=90°,则下列说法:①与∠AOC 互为邻补角的角只有一个;②与∠AOC 互为补角的角只有一个;③与∠AOC 互为邻补角的角有两个;④与∠AOC 互为补角的角有两个.其中正确的是( )
A.②③ B.①②
C.③④ D.①④
D
学以致用
小试牛刀
1 如图,直线AB,CD 相交于点O,OE 平分∠AOD,若∠DOE=36°,则∠BOC 的度数为( )
A.72°
B.90°
C.108°
D.144°
A
小试牛刀
2 如图,直线AB、CD、EF 相交于点O.
(1)写出∠COE 的邻补角;
(2)分别写出∠COE 和∠BOE 的对顶角;
(3)如果∠BOD=60°,∠BOF=90°,求∠AOF 和
∠FOC 的度数.
小试牛刀
(1)∠COE 的邻补角为∠COF 和∠EOD.
(2)∠COE 和∠BOE 的对顶角分别为∠DOF 和∠AOF.
(3)因为∠BOF=90°,
所以∠AOF=90°.
又因为∠AOC=∠BOD=60°,
所以∠FOC=∠AOF+∠AOC=90°+60°=150°.
解:
小试牛刀
3 将一张长方形纸片按图中的方式折叠,BC,BD为折痕,求∠CBD 的大小.
解:
由折叠的性质可知∠ABC=∠A′BC,
∠EBD=∠E ′BD,所以∠A′BC= ∠ABE ′,
∠E ′BD= ∠EBE ′.由∠ABE ′与∠EBE ′互为邻补角,
得∠ABE ′+∠EBE ′=180°,所以∠CBD=∠A′BC+∠E ′BD= ∠ABE ′+ ∠EBE ′= (∠ABE ′+∠EBE ′)=90°.
小试牛刀
4 如图所示,直线AB,CD 交于点O,OE 平分∠AOD,OF 平分∠DOB.
(1)若∠AOC=60°,求∠DOF 与∠DOE 的度数,并计算∠EOF 的度数;
(2)当∠AOC 的度数变化时,∠EOF 的度数是否变化?
说明理由.
小试牛刀
解:
(1)由邻补角的定义,
得∠AOD=180°-∠AOC=180°-60°=120°.
由对顶角相等,得∠BOD=∠AOC=60°.
因为OF 平分∠BOD,所以∠DOF= ∠BOD=30°.
同理∠DOE= ∠AOD=60°,
所以∠EOF=∠DOF+∠DOE=90°.
小试牛刀
(2)∠EOF 的度数不发生变化.理由如下:
因为OF 平分∠BOD,所以∠DOF= ∠BOD.
同理∠DOE= ∠AOD.
因为∠BOD+∠AOD=180°,
所以∠EOF=∠DOF+∠DOE= (∠BOD+∠AOD )=90°.
小试牛刀
5 观察下列各图,寻找对顶角(不含平角)、邻补角.
(1)如图①,图中共有________对对顶角,________对邻补角;
(2)如图②,图中共有________对对顶角,________对邻补角;
(3)如图③,图中共有________对对顶角,________对邻补角;
2
4
6
12
12
24
小试牛刀
(4)研究(1)~(3)小题中直线条数与对顶角、邻补角的对数
之间的关系,若有n 条直线相交于一点,则有多少对对
顶角,多少对邻补角?
有n(n-1)对对顶角,2n(n-1)对邻补角.
解:
课堂小结
角的名称 特征 性质 相同点 不同点
对顶角 ①两条直线相交面成的角 ②有一个公共顶点 ③没有公共边 对顶角相等 都是两直线相交而成的角,都有一个公共顶点,它们都是成对出现. 对顶角没有公共边而邻补角有一条公共边;两条直线相交时,一个有的对顶角有一个,而一个角的邻补角有两个.
邻补角 ①两条直线相交面成的角②有一个公共顶点 ③有一条公共边 邻补角互补 课堂小结
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
