【班海精品】人教版(新)七下-7.1 平面直角坐标系 第二课时【优质课件】
文档属性
| 名称 | 【班海精品】人教版(新)七下-7.1 平面直角坐标系 第二课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 10:20:52 | ||
图片预览










文档简介
(共51张PPT)
7.1 平面直角坐标系
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
0
-5
-4
-3
-2
-1
1
2
3
4
5
6
-6
7
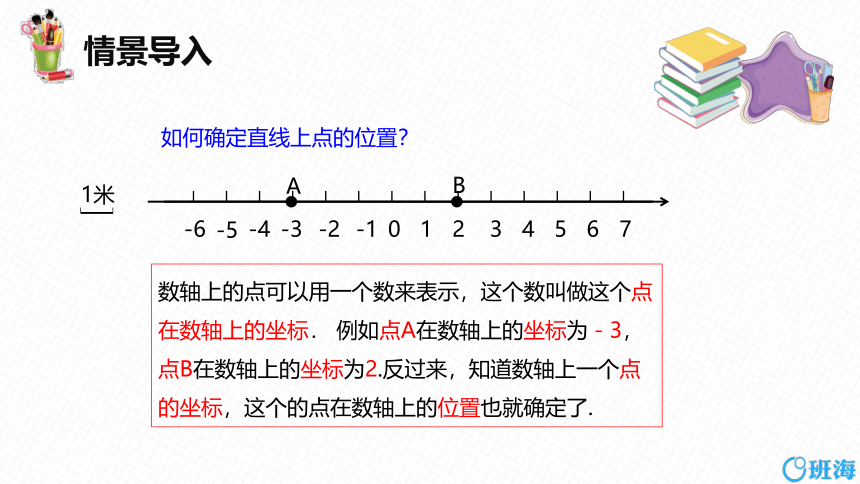
数轴上的点可以用一个数来表示,这个数叫做这个点在数轴上的坐标. 例如点A在数轴上的坐标为-3,点B在数轴上的坐标为2.反过来,知道数轴上一个点的坐标,这个的点在数轴上的位置也就确定了.
A
B
如何确定直线上点的位置?
1米
新课精讲
探索新知
1
知识点
平面直角坐标系
如何确定平面上点的位置呢?
探索新知
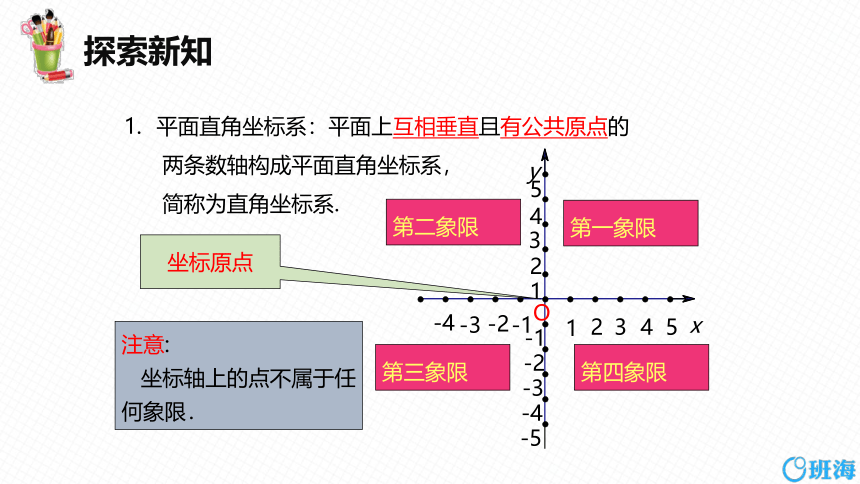
平面直角坐标系:平面上互相垂直且有公共原点的
两条数轴构成平面直角坐标系,
简称为直角坐标系.
-5
5
5
1
2
3
4
1
2
3
4
-2
-3
-4
x
-4
-3
-2
-1
-1
O
y
第一象限
第二象限
第三象限
第四象限
坐标原点
注意:
坐标轴上的点不属于任何象限.
探索新知
相关概念:
水平的数轴叫做x 轴或横轴,习惯上取向右为正方
向;铅直的数轴叫做y 轴或纵轴,取向上为正方向;
x 轴和y 轴统称坐标轴,它们的公共原点O 称为平面
直角坐标系的原点.
探索新知
下列语句不正确的是( )
A.平面直角坐标系中,两条互相垂直的数轴的交点是原点
B.平面直角坐标系所在的平面叫坐标平面
C.平面直角坐标系中x 轴、y 轴把坐标平面分成4部分
D.凡是两条互相垂直的直线都能组成平面直角坐标系
例1
D
探索新知
导引:
本题主要考查平面直角坐标系的概念.根据平面直角坐标系的概念可知A,B,C项正确.D项不正确,因为平面直角坐标系必须由数轴构成,且构成平面直角坐标系的两条数轴互相垂
直、原点重合.
探索新知
总 结
本题应用定义法,要正确理解平面直角坐标系的概念.
理解并认识平面直角坐标系必须明确:(1)建立平面直角坐标系的平面叫坐标平面;(2)平面直角坐标系必须具备:①由两条数轴组成;②这两条数轴有公共原点且互相垂直.
典题精讲
1 下列说法错误的是( )
A.平面内两条互相垂直的数轴就构成了平面直角坐标系
B.平面直角坐标系中两条数轴是互相垂直的
C.坐标平面被两条坐标轴分成了四个部分,每个部分称为象限
D.坐标轴上的点不属于任何象限
A
典题精讲
下列选项中,平面直角坐标系的画法正确的是( )
B
探索新知
2
知识点
各象限内点的坐标特征
1、直角坐标系的横轴和纵轴将平面分成 ____ 部分,
从右上方的部分说起,按逆时针方向,各部分
依次是__________、 _________ 、 _________
和__________.
2、坐标轴上的点属于哪一象限?
四
第一象限
第二象限
第三象限
第四象限
探索新知
-5
5
5
1
2
3
4
1
2
3
4
-2
-3
-4
x
-4
-3
-2
-1
-1
O
y
第一象限
第二象限
第三象限
第四象限
(+,+)
(-,+)
(-,-)
(+,-)
原点的坐标为(0,0)
各象限的坐标符号特征:
探索新知
1、点P(x,y)在第一象限 x>0,y>0.
2、点P(x,y)在第二象限 x<0,y>0.
3、点P(x,y)在第三象限 x<0,y<0.
4、点P(x,y)在第四象限 x>0,y<0.
探索新知
在平面直角坐标系(如图)中描出下列各点:
A (4,5),
B (-2,3),
C (-4,-1),
D (2.5,-2),
E (0,-4).
例2
探索新知
解:
如图,先在x 轴上找出表示4的点,再在y 轴上找出
表示5的点,过这两个点分别作x 轴和y 轴的垂线,
垂线的交点就是点A.
类似地,请你在图上
描出点B,C,D,E.
探索新知
总 结
由点的坐标确定点的位置的方法:方法一是由点的坐标的符号确定点的位置,即(+,+)的点在第一象限,(-,+)的点在第二象限,(-,-)的点在第三象限,(+,-)的点在第四象限;方法二是分别过两坐标轴上表示该点的坐标的点作两坐标轴的垂线,这两条垂线的交点位置即为该点的位置.
典题精讲
1
写出图中点A,B,C,D,E,F 的坐标.
解:
A 点的坐标为(-2,-2),
B 点的坐标为(-5,4),
C 点的坐标为(5,-4),D 点的坐标为(0,-3),
E 点的坐标为(2,5),F 点的坐标为(-3,0).
典题精讲
2
下列说法错误的是( )
A.象限内的点的坐标可用一个有序数对来表示
B.坐标轴上的点的坐标可用一个有序数对来表示
C.过点P 向x 轴作垂线,点P 与垂足之间的线段
长是点P 的纵坐标
D.过点P 向y 轴作垂线,点P 与垂足之间的线段
长不一定是点P 的横坐标
C
典题精讲
3
在平面直角坐标系中,点P (m-3,4-2m)不可能在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
C
4
在平面直角坐标系中,若点A(a,-b)在第一象限内,则点
B (a,b)所在的象限是( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
D
探索新知
3
知识点
坐标轴上点的坐标特征
点M (x,y )所处的位置 坐标特征
在x轴正半轴上:M (正,0)
在x轴负半轴上:M (负,0)
在y轴正半轴上:M (0,正)
在y轴负半轴上:M (0,负)
坐标轴上的点的坐标:
点M 在x 轴上
点M 在y 轴上
探索新知
拓展:
平行于x 轴的直线上的点的纵坐标相等;
平行于y 轴的直线上的点的横坐标相等.
探索新知
例3 已知点P (x+6,x-4)在y 轴上,则点P 的坐标是
__________.
导引:根据y 轴上点的坐标的特征可得x+6=0,得x=-6,
所以x-4=-10.故点P 的坐标是(0,-10).
(0,-10)
典题精讲
1
已知点P(0,m)在y 轴的负半轴上,则点M(-m,-m+1)在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
B
典题精讲
2
如图为A,B,C 三点在坐标平面上的位置图.若A,B,C 的x坐标的数字总和为a,y 坐标的数字总和为b,则a-b之值为何?( )
A.5
B.3
C.-3
D.-5
A
探索新知
4
知识点
构建几何图形的坐标
根据已知条件建立平面直角坐标系的步骤:
(1)分析条件,选择适当的点作为坐标原点;
(2)过原点在两个互相垂直的方向上分别作x 轴与y 轴;
(3)确定正方向,单位长度等.
探索新知
建立合适的平面直角坐标系求边长为4的正方形ABCD 的各顶点的坐标
A
B
C
D
一起探究
探索新知
0
1
2
3
4
5
-4
-3
-2
-1
3
1
2
-2
-1
-3
4
x
y
A
B
C
D
第一种类型
A (0,0), B (4,0), C (4,4),
D (0,4)
探索新知
0
1
2
3
4
5
-4
-3
-2
-1
3
1
2
-2
-1
-3
4
x
y
A
B
C
D
第二种类型
A (-4,0), B (0,0), C (0,4),
D (-4,4)
探索新知
0
1
2
3
4
5
-4
-3
-2
-1
3
1
2
-2
-1
-3
4
x
y
A
B
C
D
第三种类型
A (-2,-2), B (2,-2),
C (2,2),
D (-2,2)
同学们可以尝试更多种建立坐标系的方法
探索新知
可见:
(1)选取的坐标系不同,同一点的坐标不同;
(2)为使计算简化,证明方便,需要恰当地选取坐
标系;
(3)“恰当”意味着要充分利用图形的特点:垂直
关系、对称关系、平行关系、中点等。
探索新知
如图,长方形ABCD 的宽AB 为4,长BC 为6,按下列要求分别建立平面直角坐标系:
(1)使点D 坐标为(6,4); (2)使点D 坐标为(0,4);
(3)使点B 坐标为(-3,-2);
(4)使点B 坐标为(-3,-4).
例4
探索新知
(1)先找到坐标原点,因为点D 坐标为(6,4),所以坐标原点在点D 左边6个单位长度,下边4个单位长度处,即点B;以点B 为原点,BC,AB 所在直线分别为x 轴和y 轴,建立平面直角坐标系.
(2)(3)(4)的方法同(1).
导引:
(1)如图所示.
解:
探索新知
(2)如图所示.
(3)如图所示.
(4)如图所示.
探索新知
总 结
在几何图形中建立适当直角坐标系的一般方法:
(1)使图形中尽量多的点在坐标轴上;
(2)以某些特殊线段所在直线为x 轴或y 轴;
(3)若某图形被一条直线分得的两部分形状、大小
相同,则可以将此直线作为x 轴或y 轴;
(4)以某已知点为原点,使它的坐标为(0,0).
典题精讲
如图,长方形ABCD 的边CD 在y 轴上,点O 为CD 的中点.已知AB=4,AB 交x 轴于点E (-5,0),则点B 的坐标为( )
A.(-5,2)
B.(2,5)
C.(5,-2)
D.(-5,-2)
D
1
典题精讲
如图,正五边形ABCDE 放入某平面直角坐标系后,若顶点A,B,C,D 的坐标分别是(0,a),(-3,2),(b,m),(c,m),则点E的坐标是( )
A.(2,-3)
B.(2,3)
C.(3,2)
D.(3,-2)
C
2
易错提醒
若点P(a,b)在第二象限,则点M(b-a,a-b)在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
D
易错点:对直角坐标系内的点的坐标的符号理解不清而致错.
错解:
错解产生的原因有两个:一是对各象限内点的坐标特点没有掌握好,二是没有弄清b-a 与a-b 的符号.
诊断:
根据各象限内的点的坐标的符号特点,先判定a 与b 的符号,再确定b-a 与a - b 的符号.
解题策略:
A或B或C
学以致用
小试牛刀
在一次科学探测活动中,探测人员发现一目标在如图所示的阴影区域内,则目标的坐标可能是( )
A.(-3,300)
B.(7,-500)
C.(9,600)
D.(-2,-800)
C
1
小试牛刀
点M(a,b)为平面直角坐标系中的点.
(1)当a>0,b<0时,点M 位于第几象限?
(2)当ab>0时,点M 位于第几象限?
(3)当a 为任意非零实数,且b<0时,点M 位于第几象限?
(1)第四象限.
(2)因为ab>0,所以a>0且b>0或a<0且b<0.
所以点M位于第一象限或第三象限.
(3)第三象限或第四象限.
解:
2
小试牛刀
如图,给出格点三角形ABC.
(1)写出三角形ABC 各顶点的坐标;
(2)求出此三角形的面积.
解:
(1)A (2,2),B (-2,-1),C (3,-2).
(2)S三角形ABC=4×5- ×3×4- ×1×4- ×1×5=9.5.
3
小试牛刀
如图所示.
(1)请写出A,B,C,D,E 五点的坐标.
(2)通过观察B,C 两点的坐标,你发现了什么?线段BC 的位置有什么特点?由此你又得出什么结论?通过进一步观察D,E 两点的坐标你发现了什么?线段DE 的位置有什么特点?由此你又能得出什么结论?
4
小试牛刀
解:
(1)A (2,4),B (-1,2),C (-1,-1),D (1,-4),
E (4,-4).
(2)通过观察B,C 两点的坐标,发现B,C 两点的横坐标
相同,纵坐标不同.线段BC 与y 轴平行,与x 轴垂直.
由此可得出:若一条直线上的所有点的横坐标均相同,
纵坐标不同,则此直线与y 轴平行(或就是y 轴),也可以
说是与x 轴垂直.通过观察D,E 两点的坐标,发现D,
E 两点的纵坐标相同,横坐标不同.线段DE 与x 轴平
行,与y 轴垂直.由此可得出:若一条直线上的所有点
的纵坐标均相同,横坐标不同,则此直线与x 轴平行
(或就是x 轴),也可以说是与y 轴垂直.
小试牛刀
如图,在平面直角坐标系中,A,B,C 三点的坐标分别为
(0,1),(2,0),(2,1.5).
(1)求△ABC 的面积.
(2)如果在第二象限内有一点P(a, ),试用含a 的式子
表示四边形ABOP 的面积.
(3)在(2)的条件下,是否存在点P,使得四边形ABOP 的
面积与△ABC 的面积相等?若存在,请求出点P 的坐标;
若不存在,请说明理由.
5
小试牛刀
解:
(1)由点B (2,0),点C (2,1.5)可得CB⊥x 轴.过点A作AD⊥BC,垂足为点D,则S△ABC= BC·AD= ×1.5×2=1.5.
(2)过点P 作PE⊥y 轴,垂足为点E,则S四边形ABOP=S△AOB+
S△AOP= AO ·OB+ AO ·PE= ×1×2+ ×1×
(-a)=1- a.
(3)假设存在,依题意,有1- a=1.5,解得a=-1.
所以存在点P (-1, )使得四边形ABOP 的面积与
△ABC 的面积相等.
课堂小结
课堂小结
平面直角坐标系的三要素:
(1)两条数轴;
(2)互相告直;
(3)公共原点.
第一、二、三、四象限内点的坐标的符号依次为(+,+),(-,+),
(-,-),(+,-).
3.x 轴上的点纵坐标为0,y 轴上的点横坐标为0.
4. 建立坐标系常用的方法有:
(1)以图形上的某已知点或线段的中点为原点;
(2)以图形上某线段所在直线为x 轴(或y 轴);
(3)利用图形的轴对称性以对称轴为x 轴(或y 轴).
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
7.1 平面直角坐标系
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
0
-5
-4
-3
-2
-1
1
2
3
4
5
6
-6
7
数轴上的点可以用一个数来表示,这个数叫做这个点在数轴上的坐标. 例如点A在数轴上的坐标为-3,点B在数轴上的坐标为2.反过来,知道数轴上一个点的坐标,这个的点在数轴上的位置也就确定了.
A
B
如何确定直线上点的位置?
1米
新课精讲
探索新知
1
知识点
平面直角坐标系
如何确定平面上点的位置呢?
探索新知
平面直角坐标系:平面上互相垂直且有公共原点的
两条数轴构成平面直角坐标系,
简称为直角坐标系.
-5
5
5
1
2
3
4
1
2
3
4
-2
-3
-4
x
-4
-3
-2
-1
-1
O
y
第一象限
第二象限
第三象限
第四象限
坐标原点
注意:
坐标轴上的点不属于任何象限.
探索新知
相关概念:
水平的数轴叫做x 轴或横轴,习惯上取向右为正方
向;铅直的数轴叫做y 轴或纵轴,取向上为正方向;
x 轴和y 轴统称坐标轴,它们的公共原点O 称为平面
直角坐标系的原点.
探索新知
下列语句不正确的是( )
A.平面直角坐标系中,两条互相垂直的数轴的交点是原点
B.平面直角坐标系所在的平面叫坐标平面
C.平面直角坐标系中x 轴、y 轴把坐标平面分成4部分
D.凡是两条互相垂直的直线都能组成平面直角坐标系
例1
D
探索新知
导引:
本题主要考查平面直角坐标系的概念.根据平面直角坐标系的概念可知A,B,C项正确.D项不正确,因为平面直角坐标系必须由数轴构成,且构成平面直角坐标系的两条数轴互相垂
直、原点重合.
探索新知
总 结
本题应用定义法,要正确理解平面直角坐标系的概念.
理解并认识平面直角坐标系必须明确:(1)建立平面直角坐标系的平面叫坐标平面;(2)平面直角坐标系必须具备:①由两条数轴组成;②这两条数轴有公共原点且互相垂直.
典题精讲
1 下列说法错误的是( )
A.平面内两条互相垂直的数轴就构成了平面直角坐标系
B.平面直角坐标系中两条数轴是互相垂直的
C.坐标平面被两条坐标轴分成了四个部分,每个部分称为象限
D.坐标轴上的点不属于任何象限
A
典题精讲
下列选项中,平面直角坐标系的画法正确的是( )
B
探索新知
2
知识点
各象限内点的坐标特征
1、直角坐标系的横轴和纵轴将平面分成 ____ 部分,
从右上方的部分说起,按逆时针方向,各部分
依次是__________、 _________ 、 _________
和__________.
2、坐标轴上的点属于哪一象限?
四
第一象限
第二象限
第三象限
第四象限
探索新知
-5
5
5
1
2
3
4
1
2
3
4
-2
-3
-4
x
-4
-3
-2
-1
-1
O
y
第一象限
第二象限
第三象限
第四象限
(+,+)
(-,+)
(-,-)
(+,-)
原点的坐标为(0,0)
各象限的坐标符号特征:
探索新知
1、点P(x,y)在第一象限 x>0,y>0.
2、点P(x,y)在第二象限 x<0,y>0.
3、点P(x,y)在第三象限 x<0,y<0.
4、点P(x,y)在第四象限 x>0,y<0.
探索新知
在平面直角坐标系(如图)中描出下列各点:
A (4,5),
B (-2,3),
C (-4,-1),
D (2.5,-2),
E (0,-4).
例2
探索新知
解:
如图,先在x 轴上找出表示4的点,再在y 轴上找出
表示5的点,过这两个点分别作x 轴和y 轴的垂线,
垂线的交点就是点A.
类似地,请你在图上
描出点B,C,D,E.
探索新知
总 结
由点的坐标确定点的位置的方法:方法一是由点的坐标的符号确定点的位置,即(+,+)的点在第一象限,(-,+)的点在第二象限,(-,-)的点在第三象限,(+,-)的点在第四象限;方法二是分别过两坐标轴上表示该点的坐标的点作两坐标轴的垂线,这两条垂线的交点位置即为该点的位置.
典题精讲
1
写出图中点A,B,C,D,E,F 的坐标.
解:
A 点的坐标为(-2,-2),
B 点的坐标为(-5,4),
C 点的坐标为(5,-4),D 点的坐标为(0,-3),
E 点的坐标为(2,5),F 点的坐标为(-3,0).
典题精讲
2
下列说法错误的是( )
A.象限内的点的坐标可用一个有序数对来表示
B.坐标轴上的点的坐标可用一个有序数对来表示
C.过点P 向x 轴作垂线,点P 与垂足之间的线段
长是点P 的纵坐标
D.过点P 向y 轴作垂线,点P 与垂足之间的线段
长不一定是点P 的横坐标
C
典题精讲
3
在平面直角坐标系中,点P (m-3,4-2m)不可能在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
C
4
在平面直角坐标系中,若点A(a,-b)在第一象限内,则点
B (a,b)所在的象限是( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
D
探索新知
3
知识点
坐标轴上点的坐标特征
点M (x,y )所处的位置 坐标特征
在x轴正半轴上:M (正,0)
在x轴负半轴上:M (负,0)
在y轴正半轴上:M (0,正)
在y轴负半轴上:M (0,负)
坐标轴上的点的坐标:
点M 在x 轴上
点M 在y 轴上
探索新知
拓展:
平行于x 轴的直线上的点的纵坐标相等;
平行于y 轴的直线上的点的横坐标相等.
探索新知
例3 已知点P (x+6,x-4)在y 轴上,则点P 的坐标是
__________.
导引:根据y 轴上点的坐标的特征可得x+6=0,得x=-6,
所以x-4=-10.故点P 的坐标是(0,-10).
(0,-10)
典题精讲
1
已知点P(0,m)在y 轴的负半轴上,则点M(-m,-m+1)在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
B
典题精讲
2
如图为A,B,C 三点在坐标平面上的位置图.若A,B,C 的x坐标的数字总和为a,y 坐标的数字总和为b,则a-b之值为何?( )
A.5
B.3
C.-3
D.-5
A
探索新知
4
知识点
构建几何图形的坐标
根据已知条件建立平面直角坐标系的步骤:
(1)分析条件,选择适当的点作为坐标原点;
(2)过原点在两个互相垂直的方向上分别作x 轴与y 轴;
(3)确定正方向,单位长度等.
探索新知
建立合适的平面直角坐标系求边长为4的正方形ABCD 的各顶点的坐标
A
B
C
D
一起探究
探索新知
0
1
2
3
4
5
-4
-3
-2
-1
3
1
2
-2
-1
-3
4
x
y
A
B
C
D
第一种类型
A (0,0), B (4,0), C (4,4),
D (0,4)
探索新知
0
1
2
3
4
5
-4
-3
-2
-1
3
1
2
-2
-1
-3
4
x
y
A
B
C
D
第二种类型
A (-4,0), B (0,0), C (0,4),
D (-4,4)
探索新知
0
1
2
3
4
5
-4
-3
-2
-1
3
1
2
-2
-1
-3
4
x
y
A
B
C
D
第三种类型
A (-2,-2), B (2,-2),
C (2,2),
D (-2,2)
同学们可以尝试更多种建立坐标系的方法
探索新知
可见:
(1)选取的坐标系不同,同一点的坐标不同;
(2)为使计算简化,证明方便,需要恰当地选取坐
标系;
(3)“恰当”意味着要充分利用图形的特点:垂直
关系、对称关系、平行关系、中点等。
探索新知
如图,长方形ABCD 的宽AB 为4,长BC 为6,按下列要求分别建立平面直角坐标系:
(1)使点D 坐标为(6,4); (2)使点D 坐标为(0,4);
(3)使点B 坐标为(-3,-2);
(4)使点B 坐标为(-3,-4).
例4
探索新知
(1)先找到坐标原点,因为点D 坐标为(6,4),所以坐标原点在点D 左边6个单位长度,下边4个单位长度处,即点B;以点B 为原点,BC,AB 所在直线分别为x 轴和y 轴,建立平面直角坐标系.
(2)(3)(4)的方法同(1).
导引:
(1)如图所示.
解:
探索新知
(2)如图所示.
(3)如图所示.
(4)如图所示.
探索新知
总 结
在几何图形中建立适当直角坐标系的一般方法:
(1)使图形中尽量多的点在坐标轴上;
(2)以某些特殊线段所在直线为x 轴或y 轴;
(3)若某图形被一条直线分得的两部分形状、大小
相同,则可以将此直线作为x 轴或y 轴;
(4)以某已知点为原点,使它的坐标为(0,0).
典题精讲
如图,长方形ABCD 的边CD 在y 轴上,点O 为CD 的中点.已知AB=4,AB 交x 轴于点E (-5,0),则点B 的坐标为( )
A.(-5,2)
B.(2,5)
C.(5,-2)
D.(-5,-2)
D
1
典题精讲
如图,正五边形ABCDE 放入某平面直角坐标系后,若顶点A,B,C,D 的坐标分别是(0,a),(-3,2),(b,m),(c,m),则点E的坐标是( )
A.(2,-3)
B.(2,3)
C.(3,2)
D.(3,-2)
C
2
易错提醒
若点P(a,b)在第二象限,则点M(b-a,a-b)在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
D
易错点:对直角坐标系内的点的坐标的符号理解不清而致错.
错解:
错解产生的原因有两个:一是对各象限内点的坐标特点没有掌握好,二是没有弄清b-a 与a-b 的符号.
诊断:
根据各象限内的点的坐标的符号特点,先判定a 与b 的符号,再确定b-a 与a - b 的符号.
解题策略:
A或B或C
学以致用
小试牛刀
在一次科学探测活动中,探测人员发现一目标在如图所示的阴影区域内,则目标的坐标可能是( )
A.(-3,300)
B.(7,-500)
C.(9,600)
D.(-2,-800)
C
1
小试牛刀
点M(a,b)为平面直角坐标系中的点.
(1)当a>0,b<0时,点M 位于第几象限?
(2)当ab>0时,点M 位于第几象限?
(3)当a 为任意非零实数,且b<0时,点M 位于第几象限?
(1)第四象限.
(2)因为ab>0,所以a>0且b>0或a<0且b<0.
所以点M位于第一象限或第三象限.
(3)第三象限或第四象限.
解:
2
小试牛刀
如图,给出格点三角形ABC.
(1)写出三角形ABC 各顶点的坐标;
(2)求出此三角形的面积.
解:
(1)A (2,2),B (-2,-1),C (3,-2).
(2)S三角形ABC=4×5- ×3×4- ×1×4- ×1×5=9.5.
3
小试牛刀
如图所示.
(1)请写出A,B,C,D,E 五点的坐标.
(2)通过观察B,C 两点的坐标,你发现了什么?线段BC 的位置有什么特点?由此你又得出什么结论?通过进一步观察D,E 两点的坐标你发现了什么?线段DE 的位置有什么特点?由此你又能得出什么结论?
4
小试牛刀
解:
(1)A (2,4),B (-1,2),C (-1,-1),D (1,-4),
E (4,-4).
(2)通过观察B,C 两点的坐标,发现B,C 两点的横坐标
相同,纵坐标不同.线段BC 与y 轴平行,与x 轴垂直.
由此可得出:若一条直线上的所有点的横坐标均相同,
纵坐标不同,则此直线与y 轴平行(或就是y 轴),也可以
说是与x 轴垂直.通过观察D,E 两点的坐标,发现D,
E 两点的纵坐标相同,横坐标不同.线段DE 与x 轴平
行,与y 轴垂直.由此可得出:若一条直线上的所有点
的纵坐标均相同,横坐标不同,则此直线与x 轴平行
(或就是x 轴),也可以说是与y 轴垂直.
小试牛刀
如图,在平面直角坐标系中,A,B,C 三点的坐标分别为
(0,1),(2,0),(2,1.5).
(1)求△ABC 的面积.
(2)如果在第二象限内有一点P(a, ),试用含a 的式子
表示四边形ABOP 的面积.
(3)在(2)的条件下,是否存在点P,使得四边形ABOP 的
面积与△ABC 的面积相等?若存在,请求出点P 的坐标;
若不存在,请说明理由.
5
小试牛刀
解:
(1)由点B (2,0),点C (2,1.5)可得CB⊥x 轴.过点A作AD⊥BC,垂足为点D,则S△ABC= BC·AD= ×1.5×2=1.5.
(2)过点P 作PE⊥y 轴,垂足为点E,则S四边形ABOP=S△AOB+
S△AOP= AO ·OB+ AO ·PE= ×1×2+ ×1×
(-a)=1- a.
(3)假设存在,依题意,有1- a=1.5,解得a=-1.
所以存在点P (-1, )使得四边形ABOP 的面积与
△ABC 的面积相等.
课堂小结
课堂小结
平面直角坐标系的三要素:
(1)两条数轴;
(2)互相告直;
(3)公共原点.
第一、二、三、四象限内点的坐标的符号依次为(+,+),(-,+),
(-,-),(+,-).
3.x 轴上的点纵坐标为0,y 轴上的点横坐标为0.
4. 建立坐标系常用的方法有:
(1)以图形上的某已知点或线段的中点为原点;
(2)以图形上某线段所在直线为x 轴(或y 轴);
(3)利用图形的轴对称性以对称轴为x 轴(或y 轴).
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
