【班海精品】人教版(新)七下-8.1二元一次方程组 第二课时【优质课件】
文档属性
| 名称 | 【班海精品】人教版(新)七下-8.1二元一次方程组 第二课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 8.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 10:20:52 | ||
图片预览











文档简介
(共42张PPT)
8.1 二元一次方程组
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
含有两个未知数,并且所含未知数的项的次数都是1的方程叫做一元一次方程.
使方程左、右两边相等的未知数的值,叫做方程的解.
新课精讲
探索新知
1
知识点
二元一次方程组
我国是一个淡水资源严重缺乏的国家.有关数据显示,中国人均淡水资源占有量仅为美国人均淡水资源占有量的 , 中、美两国人均淡水资源占有量之和为13 800 m3,那么中、美两国人均淡水资源占有量各为多少
探索新知
我们假设中国人均淡水资源占有量为x m3,美国人均淡水资源占有量为y m3,根据题意得出方程y =5x.x+y=13 800.如果将这两个方程组合在一起.将会得到 它们两个都是二元一次方程,并且含有相同的未知数.
像这样共含有两个未知数的两个一次方程所组成的一组方程,叫做二元一次方程组.
探索新知
1.定义:共含有两个未知数的两个一次方程所组成的一组方程,叫做二元一次方程组.
2.要点精析:
二元一次方程组的条件:
(1)共含有两个未知数.
(2)每个方程都是一次方程.
探索新知
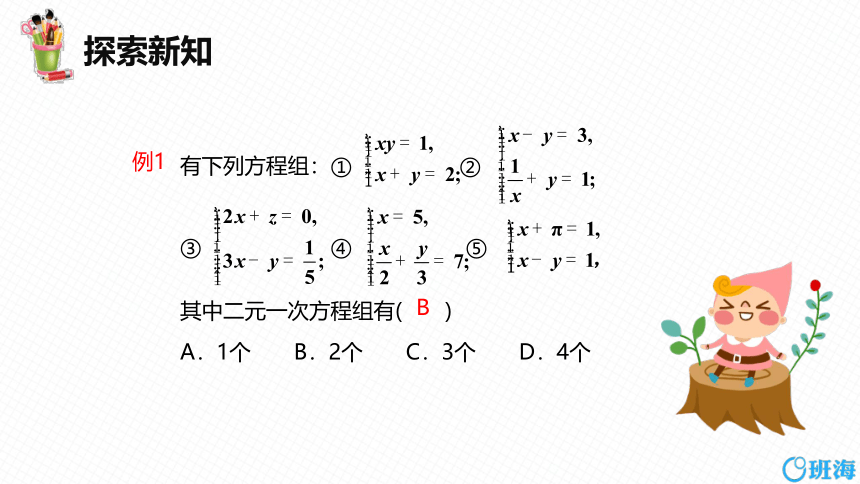
有下列方程组:① ②
③ ④ ⑤
其中二元一次方程组有( )
A.1个 B.2个 C.3个 D.4个
B
例1
探索新知
导引:①方程组中第一个方程含未知数的项xy 的次数不是1;
②方程组中第二个方程不是整式方程;
③方程组中共有3个未知数.
只有④⑤满足,其中⑤中的π是常数.
探索新知
总 结
识别一个方程组是否为二元一次方程组的方法:
一看方程组中的方程是否都是整式方程;
二看方程组中是不是只含有两个未知数;
三看含未知数的项的次数是不是都为1.
典题精讲
1
下列方程组中,是二元一次方程组的是( )
A. B.
C. D.
D
典题精讲
2
下列不属于二元一次方程组的是( )
A. B.
C. D.
D
探索新知
2
知识点
二元一次方程组的解
二元一次方程组的解:
定义:二元一次方程组中各个方程的公共解,
叫做这个二元一次方程组的解.
探索新知
根据下表所给出的x的值及关于x,y 的二元一次方程,求出相应的y 的值,并填入表内.
请你从上表中找出二元一次方程组 的解.
根据二元一次方程组的解的概念,找出同时满足两个二元一次方程的公共解,即为二元一次方程组的解.
x 1 2 3 4 5 6 7 8 9 10
y=2x
y=x+5
例2
导引:
探索新知
填表如下:
从表中可以看出
解,也是二元一次方程 y=x+5的解,
所以二元一次方程组
x 1 2 3 4 5 6 7 8 9 10
y=2x 2 4 6 8 10 12 14 16 18 20
y=x+5 6 7 8 9 10 11 12 13 14 15
既是二元一次方程y=2x 的
的解是
解:
探索新知
总 结
本题运用定义法,检验一组数是不是某个二元一次
方程组的解,常用的方法是将这组数分别代入方程组的
每个方程中去,只要这组数满足每个方程,才能说这组
数是此方程组的解;只要发现这组数不满足其中一个方
程,即可判定这组数不是二元一次方程组的解.
典题精讲
关于x,y 的方程组 的解是
其中y 的值被盖住了,不过仍能求出p,则p 的
值是( )
A.- B.
C.- D.
1
A
典题精讲
已知二元一次方程组 下面说法正确的是( )
A.同时适合方程①和方程②的x,y 的值是方程组的解
B.适合方程①的x,y 的值是方程组的解
C.适合方程②的x,y 的值是方程组的解
D.适合方程①或方程②的x,y 的值,一定是方程组的解
2
A
典题精讲
方程5x+2y=-9与下列方程构成的方程组的解为 的是( )
A.x+2y=1
B.3x+2y=-8
C.5x+4y=-3
D.3x-4y=-8
3
D
探索新知
3
知识点
建二元一次方程组的模型
某中学组织七年级学生春游,原计划租用45座的客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出一辆车,且其余客车恰好坐满,试问七年级学生人数是多少?原计划租用45座客车多少辆?(只列方程组)
例3
探索新知
此题中有两个未知量——七年级学生人数和原计划
租用45座客车的辆数,有两个等量关系:
(1)45×45座客车的辆数+15=七年级学生人数;
(2)60×(45座客车的辆数-1)=七年级学生人数.
设七年级学生有x人,原计划租用y 辆45座客车.
根据题意,有
导引:
解:
探索新知
总 结
这是与现实生活有关的方程类问题,解决这类问题的关键是建立恰当的数学模型.列方程组的方法可类比列一元一次方程的方法;不同的是根据实际问题找出题目中的两个等量关系,并分别列出相应的方程.
典题精讲
对下面的问题,列出二元一次方程组,并根据问题的实际意义,找出问题的解. 加工某种产品需经两道工序,第一道工序每人每天可完成900件,第二道工序每人 每天可完成1 200件. 现有7位工人参加这两道工序,应怎样安排人力,才能使每 天第一、第二道工序所完成的件数相等?
1
典题精讲
设应安排x人参加第一道工序,y人参加第二道工序,根据题意得
方程组整理为 因为x,y 只能取正整数,并且都小于7,可以看出当x=4,y=3时能满足方程组,所以应安排4人参加第一道工序,3人参加第二道工序.
解:
典题精讲
若单项式5x a+by 3与 x 5y a-b是同类项,则a,b
的值分别为( )
A.a=4,b=1
B.a=-4,b=1
C.a=4,b=-1
D.a=-4,b=-1
2
A
典题精讲
端午节前夕,某超市用1 680元购进A、B 两种商品共60件,其中A 型商品每件 24元,B 型商品每件36元.设购买A 型商品x 件、B 型商品y 件,依题意列方程组正确的是( )
A. B.
C. D.
3
B
易错提醒
判断 是否是二元一次方程组 的解.
解:
将 分别代入方程①和方程②中,得4x+2y
=2成立,x+y=-1不成立,所以 不是方程组 的解.
易错点:对二元一次方程组的解理解不透彻,导致在检验时出错
学以致用
小试牛刀
若二元一次方程组 的解为 则a-b=( )
A.1 B.3
C.- D.
D
1
小试牛刀
我国古代数学名著《孙子算经》中记载了一道题,大意是:100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦,问有多少匹大马、多少匹小马?若设大马有x 匹,小马有y 匹,那么可列方程组为( )
A. B.
C. D.
C
2
小试牛刀
已知下列五对数值:
(1)哪几对数值是方程 x-y=6的解?
(2)哪几对数值是方程2x+31y=-11的解?
(3)指出方程组 的解.
3
小试牛刀
(1)①②③是方程 x-y=6的解.
(2)③④⑤是方程2x+31y=-11的解.
(3)③是方程组 的解.
解:
小试牛刀
世界杯足球赛期间,小李在网上预定了小组赛和淘汰赛两个阶段的球票共10张,总价为5 800元,其中小组赛球票每张550元,淘汰赛球票每张700元.设小李预定的小组赛的球票有x张,淘汰赛的球票有y 张.
(1)你能列出相应的方程组吗?
(2) 是方程组的解吗?小李预定的小组赛和淘汰赛的球票分别为多少张?
4
小试牛刀
(1)由题意可得
(2) 是方程组的解.小李预定的小组赛的球票为8张,淘汰赛的球票为2张.
解:
小试牛刀
阅读下面情境:甲、乙两人共同解方
程组 由于甲看错了方程①中的a,
得到方程组的解为 乙看错了方程②中的b,得到方程组的解为 试求出a,b 的正确值,并计算 的值.
5
小试牛刀
将 代入②,得b=10;
将 代入①,得a=-1.
所以
解:
小试牛刀
如图,它是一个正方体的展开图,若正方体相对面上的数或式子的值相等,请列出符合条件的所有二元一次方程组.
因为正方体相对面上的数
或式子的值相等,
所以2x+y=-3,x=1,3x+y=-2.
所以可列出3个方程组:
解:
6
课堂小结
课堂小结
1.二元一次方程组的特征:
(1)整个方程组(不是方程组中的每个方程)含有且只含有两个未知数;
(2)每个方程都是一次方程;
(3)每个方程都是整式方程.
课堂小结
2. 二元一次方程组的解:
(1)常见的二元一次方程组一般都只有一组解(有时无解);
(2)只要告诉一组值是某个二元一次方程组的解,
就说明这组值是方程组中每个方程的解;
(3)方程组的解一定是方程组中每个方程的解;而
方程组中的某一方程的解不一定是方程组的解.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
8.1 二元一次方程组
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
含有两个未知数,并且所含未知数的项的次数都是1的方程叫做一元一次方程.
使方程左、右两边相等的未知数的值,叫做方程的解.
新课精讲
探索新知
1
知识点
二元一次方程组
我国是一个淡水资源严重缺乏的国家.有关数据显示,中国人均淡水资源占有量仅为美国人均淡水资源占有量的 , 中、美两国人均淡水资源占有量之和为13 800 m3,那么中、美两国人均淡水资源占有量各为多少
探索新知
我们假设中国人均淡水资源占有量为x m3,美国人均淡水资源占有量为y m3,根据题意得出方程y =5x.x+y=13 800.如果将这两个方程组合在一起.将会得到 它们两个都是二元一次方程,并且含有相同的未知数.
像这样共含有两个未知数的两个一次方程所组成的一组方程,叫做二元一次方程组.
探索新知
1.定义:共含有两个未知数的两个一次方程所组成的一组方程,叫做二元一次方程组.
2.要点精析:
二元一次方程组的条件:
(1)共含有两个未知数.
(2)每个方程都是一次方程.
探索新知
有下列方程组:① ②
③ ④ ⑤
其中二元一次方程组有( )
A.1个 B.2个 C.3个 D.4个
B
例1
探索新知
导引:①方程组中第一个方程含未知数的项xy 的次数不是1;
②方程组中第二个方程不是整式方程;
③方程组中共有3个未知数.
只有④⑤满足,其中⑤中的π是常数.
探索新知
总 结
识别一个方程组是否为二元一次方程组的方法:
一看方程组中的方程是否都是整式方程;
二看方程组中是不是只含有两个未知数;
三看含未知数的项的次数是不是都为1.
典题精讲
1
下列方程组中,是二元一次方程组的是( )
A. B.
C. D.
D
典题精讲
2
下列不属于二元一次方程组的是( )
A. B.
C. D.
D
探索新知
2
知识点
二元一次方程组的解
二元一次方程组的解:
定义:二元一次方程组中各个方程的公共解,
叫做这个二元一次方程组的解.
探索新知
根据下表所给出的x的值及关于x,y 的二元一次方程,求出相应的y 的值,并填入表内.
请你从上表中找出二元一次方程组 的解.
根据二元一次方程组的解的概念,找出同时满足两个二元一次方程的公共解,即为二元一次方程组的解.
x 1 2 3 4 5 6 7 8 9 10
y=2x
y=x+5
例2
导引:
探索新知
填表如下:
从表中可以看出
解,也是二元一次方程 y=x+5的解,
所以二元一次方程组
x 1 2 3 4 5 6 7 8 9 10
y=2x 2 4 6 8 10 12 14 16 18 20
y=x+5 6 7 8 9 10 11 12 13 14 15
既是二元一次方程y=2x 的
的解是
解:
探索新知
总 结
本题运用定义法,检验一组数是不是某个二元一次
方程组的解,常用的方法是将这组数分别代入方程组的
每个方程中去,只要这组数满足每个方程,才能说这组
数是此方程组的解;只要发现这组数不满足其中一个方
程,即可判定这组数不是二元一次方程组的解.
典题精讲
关于x,y 的方程组 的解是
其中y 的值被盖住了,不过仍能求出p,则p 的
值是( )
A.- B.
C.- D.
1
A
典题精讲
已知二元一次方程组 下面说法正确的是( )
A.同时适合方程①和方程②的x,y 的值是方程组的解
B.适合方程①的x,y 的值是方程组的解
C.适合方程②的x,y 的值是方程组的解
D.适合方程①或方程②的x,y 的值,一定是方程组的解
2
A
典题精讲
方程5x+2y=-9与下列方程构成的方程组的解为 的是( )
A.x+2y=1
B.3x+2y=-8
C.5x+4y=-3
D.3x-4y=-8
3
D
探索新知
3
知识点
建二元一次方程组的模型
某中学组织七年级学生春游,原计划租用45座的客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出一辆车,且其余客车恰好坐满,试问七年级学生人数是多少?原计划租用45座客车多少辆?(只列方程组)
例3
探索新知
此题中有两个未知量——七年级学生人数和原计划
租用45座客车的辆数,有两个等量关系:
(1)45×45座客车的辆数+15=七年级学生人数;
(2)60×(45座客车的辆数-1)=七年级学生人数.
设七年级学生有x人,原计划租用y 辆45座客车.
根据题意,有
导引:
解:
探索新知
总 结
这是与现实生活有关的方程类问题,解决这类问题的关键是建立恰当的数学模型.列方程组的方法可类比列一元一次方程的方法;不同的是根据实际问题找出题目中的两个等量关系,并分别列出相应的方程.
典题精讲
对下面的问题,列出二元一次方程组,并根据问题的实际意义,找出问题的解. 加工某种产品需经两道工序,第一道工序每人每天可完成900件,第二道工序每人 每天可完成1 200件. 现有7位工人参加这两道工序,应怎样安排人力,才能使每 天第一、第二道工序所完成的件数相等?
1
典题精讲
设应安排x人参加第一道工序,y人参加第二道工序,根据题意得
方程组整理为 因为x,y 只能取正整数,并且都小于7,可以看出当x=4,y=3时能满足方程组,所以应安排4人参加第一道工序,3人参加第二道工序.
解:
典题精讲
若单项式5x a+by 3与 x 5y a-b是同类项,则a,b
的值分别为( )
A.a=4,b=1
B.a=-4,b=1
C.a=4,b=-1
D.a=-4,b=-1
2
A
典题精讲
端午节前夕,某超市用1 680元购进A、B 两种商品共60件,其中A 型商品每件 24元,B 型商品每件36元.设购买A 型商品x 件、B 型商品y 件,依题意列方程组正确的是( )
A. B.
C. D.
3
B
易错提醒
判断 是否是二元一次方程组 的解.
解:
将 分别代入方程①和方程②中,得4x+2y
=2成立,x+y=-1不成立,所以 不是方程组 的解.
易错点:对二元一次方程组的解理解不透彻,导致在检验时出错
学以致用
小试牛刀
若二元一次方程组 的解为 则a-b=( )
A.1 B.3
C.- D.
D
1
小试牛刀
我国古代数学名著《孙子算经》中记载了一道题,大意是:100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦,问有多少匹大马、多少匹小马?若设大马有x 匹,小马有y 匹,那么可列方程组为( )
A. B.
C. D.
C
2
小试牛刀
已知下列五对数值:
(1)哪几对数值是方程 x-y=6的解?
(2)哪几对数值是方程2x+31y=-11的解?
(3)指出方程组 的解.
3
小试牛刀
(1)①②③是方程 x-y=6的解.
(2)③④⑤是方程2x+31y=-11的解.
(3)③是方程组 的解.
解:
小试牛刀
世界杯足球赛期间,小李在网上预定了小组赛和淘汰赛两个阶段的球票共10张,总价为5 800元,其中小组赛球票每张550元,淘汰赛球票每张700元.设小李预定的小组赛的球票有x张,淘汰赛的球票有y 张.
(1)你能列出相应的方程组吗?
(2) 是方程组的解吗?小李预定的小组赛和淘汰赛的球票分别为多少张?
4
小试牛刀
(1)由题意可得
(2) 是方程组的解.小李预定的小组赛的球票为8张,淘汰赛的球票为2张.
解:
小试牛刀
阅读下面情境:甲、乙两人共同解方
程组 由于甲看错了方程①中的a,
得到方程组的解为 乙看错了方程②中的b,得到方程组的解为 试求出a,b 的正确值,并计算 的值.
5
小试牛刀
将 代入②,得b=10;
将 代入①,得a=-1.
所以
解:
小试牛刀
如图,它是一个正方体的展开图,若正方体相对面上的数或式子的值相等,请列出符合条件的所有二元一次方程组.
因为正方体相对面上的数
或式子的值相等,
所以2x+y=-3,x=1,3x+y=-2.
所以可列出3个方程组:
解:
6
课堂小结
课堂小结
1.二元一次方程组的特征:
(1)整个方程组(不是方程组中的每个方程)含有且只含有两个未知数;
(2)每个方程都是一次方程;
(3)每个方程都是整式方程.
课堂小结
2. 二元一次方程组的解:
(1)常见的二元一次方程组一般都只有一组解(有时无解);
(2)只要告诉一组值是某个二元一次方程组的解,
就说明这组值是方程组中每个方程的解;
(3)方程组的解一定是方程组中每个方程的解;而
方程组中的某一方程的解不一定是方程组的解.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
