【班海精品】人教版(新)七下-8.2 消元——解二元一次方程组 第二课时【优质课件】
文档属性
| 名称 | 【班海精品】人教版(新)七下-8.2 消元——解二元一次方程组 第二课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 10:20:52 | ||
图片预览










文档简介
(共58张PPT)
8.2 消元——解二元一次方程组
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
主要步骤:
基本思路:
写解
求解
代入
把变形后的方程代入到另一个方程中,消去一个元
分别求出两个未知数的值
写出方程组的解
变形
用含有一个未知数的代数式表示另一个未知数, 写成y=ax+b 或x=ay+b
消元: 二元
1、解二元一次方程组的基本思路是什么?
2、用代入法解方程的步骤是什么?
一元
新课精讲
探索新知
1
知识点
直接加减消元
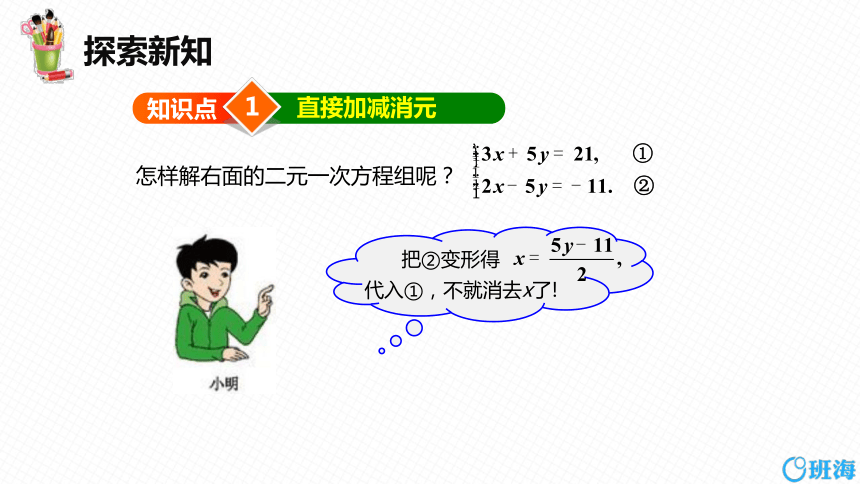
把②变形得 代入①,不就消去x了!
怎样解右面的二元一次方程组呢?
探索新知
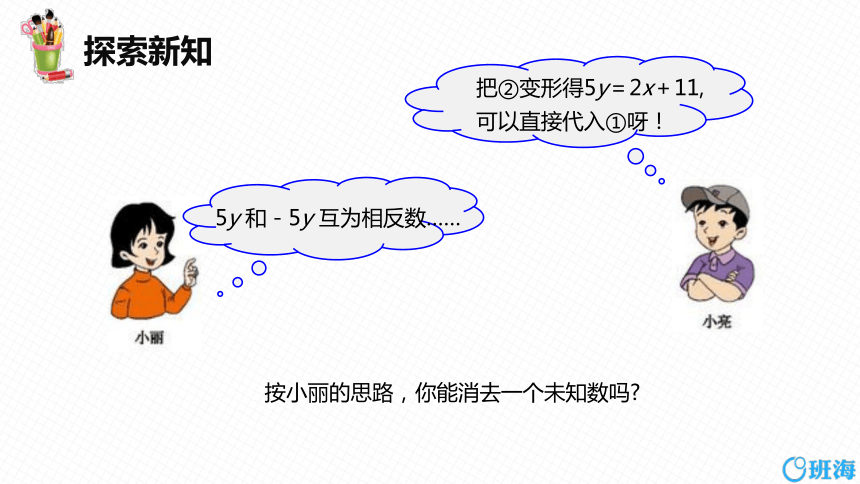
按小丽的思路,你能消去一个未知数吗
把②变形得5y=2x+11,可以直接代入①呀!
5y 和-5y 互为相反数……
探索新知
两个方程相加,可以得到5x = 10,
x = 2.
将x = 2代入①,得 6 + 5y = 21,
y = 3.
所以方程组
的解是
探索新知
加减法定义:当二元一次方程组的两个方程中同
一未知数的系数相反或相等时,把这两个方程的两边
分别相加或相减,就能消去这个未知数,得到一个一
元一次方程,这种方法叫做加减消元法,简称加减法.
探索新知
用加减法解方程组:
例1
导引:
两个方程中x 的系数相同,y 的系数互为相反数,
这样可以把两个方程相加消去y,或者把两个方
程相减消去x.
方法一:①+②,得6x=12,解得x=2.把x=2
代入②,得3×2+7y=13,解得y=1.
所以原方程组的解为
解:
探索新知
方法二:①-②,得-14y=-14,解得y=1.
把y=1代入①,得3x-7×1=-1,解得x=2.
所以原方程组的解为
探索新知
当二元一次方程组的两个方程中同一未知数
的系数相反或相等时,把这两个方程的两边分别相
加或相减,就能消去这个未知数,得到一个一元一
次方程,然后解答方程即可.
总 结
典题精讲
1 方程组 中,x 的系数的特点是_______,
方程组 中,y 的系数的特点是 ____________,
这两个方程组用________消元法解较简便.
相等
互为相反数
加减
典题精讲
2
方程组 既可以用__________消去未知数_____;也可以用 消去未知数______.
①+②
y
①-②或②-①
x
典题精讲
3 用加减法解方程组 时,①-②得( )
A.5y=2
B.-11y=8
C.-11y=2
D.5y=8
A
典题精讲
4
解方程组 时,用加减消元法最简便的是( )
A.①+②
B.①-②
C.①×2-②×3
D.①×3+②×2
A
探索新知
2
知识点
先变形,再加减消元
如果二元一次方程组的未知数的系数相同或互为相反数,我们可以运用加减法来解.那么对于一些系数不同或不互为相反数的二元一次方程组,还能用加减法来解吗
探索新知
用加减法解方程组:
例2
这两个方程中没有同一个未知数的系数相反或相
等,直接加减这两 个方程不能消元. 我们对方程
变形,使得这两个方程中某个未知数的系数相反
或相等.
分析:
探索新知
解:
①×3,得 9x+12y=48. ③
②×2,得 10x-12y =66. ④
③+④,得19x=114,
即 x=6.
把x=6代入① ,得 3×6+4y =16,
4y= -2,
y=
所以这个方程组的解是
探索新知
例3 解方程组:
导引:方程组中,两个方程中y 的系数的绝对值成倍数关系,
方程②乘以3就可与方程①相加消去y.
解: 由②×3,得 51x-9y=222,③
由①+③,得 59x=295,解得 x=5.
把x=5代入①,得8×5+9y=73,解得
所以原方程组的解为
典题精讲
1 用加减法解方程组:
典题精讲
①+②,得4x=8,
解这个方程,得x=2.
把x=2代入①,得y= .
因此,这个方程组的解是
解:
典题精讲
①×2,得10x+4y=50.③
③-②,得7x=35,解这个方程,得x=5.
把x=5代入①,得5×5+2y=25,y=0.
因此,这个方程组的解是
解:
典题精讲
①×3,得6x+15y=24.③
②×2,得6x+4y=10.④
③-④,得11y=14,y= .
把y= 代入①,得2x+5× =8,x= .
因此,这个方程组的解是
解:
典题精讲
①×2,得4x+6y=12.③
②×3,得9x-6y=-6.④
③+④,得13x=6,x= .
把x= 代入①,得2× +3y=6,y= .
因此,这个方程组的解是
解:
典题精讲
利用加减消元法解方程组
下列做法正确的是( )
A.要消去y,可以将①×5+②×2
B.要消去x,可以将①×3+②×(-5)
C.要消去y,可以将①×5+②×3
D.要消去x,可以将①×(-5)+②×2
2
D
探索新知
3
知识点
解方程组的应用
2台大收割机和5台小收割机同时工作2 h共收割小麦3. 6 hm2 ,
3台大收割机和2台小收割机同时工作5 h共收割小麦8 hm2. 1台大收割机和1台小收割机每小时各收割小麦多少公顷?
例4
探索新知
导引:
如果1台大收割机和1台小收割机每小时各收割小麦x hm2和y hm2,那么2台大收割机和5台小收割机同时工作1 h共收割小麦_____________ hm2,3台大收割机和2台小收割机同时工作1 h共收割小麦________hm2. 由此考虑两种情况下的工作量.
探索新知
解:
设1台大收割机和1台小收割机每小时各收割小麦x hm2和y hm2. 根据两种工作方式中的相等关系,
得方程组
去括号,得
②-①,得11x=4.4.
解这个方程,得x=0.4.
把x=0.4代入①,得y=0.2.
因此,这个方程组的解是
答:1台大收割机和1台小收割机每小时各收割小麦0. 4 hm2和0. 2 hm2.
探索新知
例5 解方程组:
导引:方程①和②中x,y 的系数的绝对值都不相等,也不成
倍数关系,应取系数的绝对值的最小公倍数6,可以
先消去x,也可以先消去 y.
探索新知
解:方法一:①×3,得6x+9y=9.③
②×2,得6x+4y=22.④
③-④,得5y=-13,即
把
解得
所以这个方程组的解为
代入①,得
探索新知
方法二:①×2,得4x+6y=6.⑤
②×3,得9x+6y=33.⑥
⑥-⑤,得5x=27,解得
把
解得
所以这个方程组的解为
代入①,得
探索新知
总 结
用加减消元法解二元一次方程组时,一般有三种情况:
①方程组中某个未知数的系数的绝对值相等,则直接利用加减法求解;
②方程组中任一个未知数的系数的绝对值都不相等,但某个未知数的系数的绝对值成倍数关系,则其中一个方程乘这个倍数后再利用加减法求解;
③方程组中任一个未知数的系数的绝对值既不相等,也不成倍数关系,可利用最小公倍数的知识,把两个方程都适当地乘一个数,使某个未知数的系数的绝对值相等,然后再利用加减法求解.
探索新知
一条船顺流航行,每小时行20 km;逆流航行,每小时行16 km. 求轮船在静水中的速度与水的流速.
1
设轮船在静水中的速度为每小时x km,水的流速为每小时y km.依题意,得
①+②,得2x=36,x=18.把x=18代入①,得y=2.
所以原方程组的解为
答:轮船在静水中的速度为每小时18 km,水的流速为每小时2 km.
解:
探索新知
运输360 t化肥,装载了 6节火车车厢和15辆汽车;运输440 t化肥,装载了8节火车车厢和10辆汽车. 每节火车车厢与每辆汽车平均各装多少吨化肥?
2
设每节火车车厢平均装x t化肥,
每辆汽车平均装y t化肥.
依题意,得
解:
典题精讲
①×2,得12x+30y=720.③
②×3,得24x+30y=1 320.④
④-③,得12x=600,x=50.
把x=50代入①,得
6×50+15y=360,y=4.
所以原方程组的解为
答:每节火车车厢平均装50 t化肥,每辆汽车平均装4 t化肥.
典题精讲
若方程组 的解也是二元一次方程5x-my=-11的一个解,则m 的值等于( )
A.5
B.-7
C.-5
D.7
3
D
易错提醒
解方程组:
解:
令x+y=a,x-y=b,则原方程组可化为
解得 所以x+y=7,x-y=1,将它们组成新方程组,即 解得
所以原方程组的解是
易错点:误将换元的解当作原方程组的解(换元法)
学以致用
小试牛刀
已知x,y 满足方程组 则x+y 的值为( )
A.9
B.7
C.5
D.3
C
1
小试牛刀
用加减法解方程组 时,要使两个方程中同一未知数的系数相等或相反,有以下四种变形的结果:
其中变形正确的是( )
A.①② B.③④ C.①③ D.②④
B
2
小试牛刀
小明在某商店购买商品A,B 共两次,这两次购买商品A,B的数量和费用如表:
购买商品A的数量/个 购买商品B 的数量/个 购买总
费用/元
第一次购物 4 3 93
第二次购物 6 6 162
若小丽需要购买3个商品A 和2个商品B,则她要花费( )
A.64元 B.65元 C.66元 D.67元
C
3
小试牛刀
选择适当的方法解方程组.
(1)
将①代入②,得2y+9=11,所以y=1.
将y=1代入①,得x-1=3. 所以x=4.
所以原方程组的解为
解:
4
小试牛刀
①×10-②,得25y=10,所以y= .
将y= 代入②,得5x-5× =-4,所以x=0.
所以原方程组的解是
小试牛刀
阅读下列内容,回答问题:
解方程组时,有时可根据方程的未知数的系数特征,将几个方程直接进行整体加减.如解方程组
①+②,得10x+10y=30,
即x+y=3,③
将①变形为3x+3y+5y=14,即3(x+y)+5y=14.④
把③代入④,得3×3+5y=14,求得y=1,
再把y=1代入③,得x=3-1,即x=2.
5
小试牛刀
从而比较简便地求得原方程组的解为
上述这种方法我们称它为“整体加减法”,你若留心观察,
有很多方程组都可采用此法解,请你用这种方法解方程
组
小试牛刀
①+②,得4 035x+4 035y=4 035,x+y=1.③
将①变形为2 017x+2 017y+y=2 016,
即2 017(x+y )+y=2 016,④
将③代入④,得2 017×1+y=2 016,解得y=-1.
再将y=-1代入③,得x=2.
所以原方程组的解为
解:
小试牛刀
解方程组 时,若设 =m, =n,则原方程组可
变形为关于m,n 的方程组
解这个方程组得到它的解为
由 =5, =-4,求得原方程组的解为利用上述方法
解方程组:
6
小试牛刀
设 =m, =n,
则原方程组可变形为
解这个方程组得到它的解为
由 =3, =-2,
求得原方程组的解为
解:
小试牛刀
已知关于x,y 的二元一次方程组
的解互为相反数,求k 的值.
解方程组 得
由关于x,y 的二元一次方程组 的解
互为相反数,可得2k+3-2-k=0,解得k=-1.
解:
7
小试牛刀
小明想从“天猫”某网店购买计算器,经查询,某品牌A型号计算器的单价比B型号计算器的单价多10元,5台A型号的计算器与7台B型号的计算器的价钱相同,问A,B两种型号计算器的单价分别是多少?
设A型号计算器的单价为x 元,B型号计算器的单价
为y元,依题意,得 解得
答:A型号计算器的单价为35元,B型号计算器的单价为25元.
解:
8
小试牛刀
如图①,在3×3的方格中,填写了一些整式,使得每行3个数、每列3个数、对角线上3个数的和均相等.
(1)求x,y 的值;
(2)根据求得的x,y,a,b,c 的值完成图②.
9
小试牛刀
(1)由题意,得
解得
(2)由(1)知x=-1,所以3+4+x=6,
所以 解得
如图.
解:
3 4 -1
-2 2 6
5 0 1
小试牛刀
请根据图中提供的信息,回答下列问题:
(1)一个暖瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的暖瓶和水杯.为了迎接新年,两家商场都在搞促销活动.甲商场规定:这两种商品都打九折;乙商场规定:买一个暖瓶赠送一个水杯.若某单位想要买4个暖瓶和15个水杯,请问选择哪家商场购买更合算?并说明理由.
10
小试牛刀
(1)设一个暖瓶与一个水杯分别为x 元、y 元,
由题意,得 解得
所以一个暖瓶与一个水杯分别为30元、8元.
(2)在乙商场购买更合算.理由:若该单位在甲商场购买,则需钱数为4×30×0.9+15×8×0.9=216(元);若在乙商场购买,则需钱数为4×30+(15-4)×8=208(元).所以在乙商场购买更合算.
解:
课堂小结
课堂小结
用加减消元法解二元一次方程组的一般步骤:
(1)变形:将方程组中某一未知数的系数变为相等或相反.
(2)加减:消去一个未知数.
(3)求解:得到一个未知数的值.
(4)回代:求另一个未知数的值.
(5)写出解.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
8.2 消元——解二元一次方程组
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
主要步骤:
基本思路:
写解
求解
代入
把变形后的方程代入到另一个方程中,消去一个元
分别求出两个未知数的值
写出方程组的解
变形
用含有一个未知数的代数式表示另一个未知数, 写成y=ax+b 或x=ay+b
消元: 二元
1、解二元一次方程组的基本思路是什么?
2、用代入法解方程的步骤是什么?
一元
新课精讲
探索新知
1
知识点
直接加减消元
把②变形得 代入①,不就消去x了!
怎样解右面的二元一次方程组呢?
探索新知
按小丽的思路,你能消去一个未知数吗
把②变形得5y=2x+11,可以直接代入①呀!
5y 和-5y 互为相反数……
探索新知
两个方程相加,可以得到5x = 10,
x = 2.
将x = 2代入①,得 6 + 5y = 21,
y = 3.
所以方程组
的解是
探索新知
加减法定义:当二元一次方程组的两个方程中同
一未知数的系数相反或相等时,把这两个方程的两边
分别相加或相减,就能消去这个未知数,得到一个一
元一次方程,这种方法叫做加减消元法,简称加减法.
探索新知
用加减法解方程组:
例1
导引:
两个方程中x 的系数相同,y 的系数互为相反数,
这样可以把两个方程相加消去y,或者把两个方
程相减消去x.
方法一:①+②,得6x=12,解得x=2.把x=2
代入②,得3×2+7y=13,解得y=1.
所以原方程组的解为
解:
探索新知
方法二:①-②,得-14y=-14,解得y=1.
把y=1代入①,得3x-7×1=-1,解得x=2.
所以原方程组的解为
探索新知
当二元一次方程组的两个方程中同一未知数
的系数相反或相等时,把这两个方程的两边分别相
加或相减,就能消去这个未知数,得到一个一元一
次方程,然后解答方程即可.
总 结
典题精讲
1 方程组 中,x 的系数的特点是_______,
方程组 中,y 的系数的特点是 ____________,
这两个方程组用________消元法解较简便.
相等
互为相反数
加减
典题精讲
2
方程组 既可以用__________消去未知数_____;也可以用 消去未知数______.
①+②
y
①-②或②-①
x
典题精讲
3 用加减法解方程组 时,①-②得( )
A.5y=2
B.-11y=8
C.-11y=2
D.5y=8
A
典题精讲
4
解方程组 时,用加减消元法最简便的是( )
A.①+②
B.①-②
C.①×2-②×3
D.①×3+②×2
A
探索新知
2
知识点
先变形,再加减消元
如果二元一次方程组的未知数的系数相同或互为相反数,我们可以运用加减法来解.那么对于一些系数不同或不互为相反数的二元一次方程组,还能用加减法来解吗
探索新知
用加减法解方程组:
例2
这两个方程中没有同一个未知数的系数相反或相
等,直接加减这两 个方程不能消元. 我们对方程
变形,使得这两个方程中某个未知数的系数相反
或相等.
分析:
探索新知
解:
①×3,得 9x+12y=48. ③
②×2,得 10x-12y =66. ④
③+④,得19x=114,
即 x=6.
把x=6代入① ,得 3×6+4y =16,
4y= -2,
y=
所以这个方程组的解是
探索新知
例3 解方程组:
导引:方程组中,两个方程中y 的系数的绝对值成倍数关系,
方程②乘以3就可与方程①相加消去y.
解: 由②×3,得 51x-9y=222,③
由①+③,得 59x=295,解得 x=5.
把x=5代入①,得8×5+9y=73,解得
所以原方程组的解为
典题精讲
1 用加减法解方程组:
典题精讲
①+②,得4x=8,
解这个方程,得x=2.
把x=2代入①,得y= .
因此,这个方程组的解是
解:
典题精讲
①×2,得10x+4y=50.③
③-②,得7x=35,解这个方程,得x=5.
把x=5代入①,得5×5+2y=25,y=0.
因此,这个方程组的解是
解:
典题精讲
①×3,得6x+15y=24.③
②×2,得6x+4y=10.④
③-④,得11y=14,y= .
把y= 代入①,得2x+5× =8,x= .
因此,这个方程组的解是
解:
典题精讲
①×2,得4x+6y=12.③
②×3,得9x-6y=-6.④
③+④,得13x=6,x= .
把x= 代入①,得2× +3y=6,y= .
因此,这个方程组的解是
解:
典题精讲
利用加减消元法解方程组
下列做法正确的是( )
A.要消去y,可以将①×5+②×2
B.要消去x,可以将①×3+②×(-5)
C.要消去y,可以将①×5+②×3
D.要消去x,可以将①×(-5)+②×2
2
D
探索新知
3
知识点
解方程组的应用
2台大收割机和5台小收割机同时工作2 h共收割小麦3. 6 hm2 ,
3台大收割机和2台小收割机同时工作5 h共收割小麦8 hm2. 1台大收割机和1台小收割机每小时各收割小麦多少公顷?
例4
探索新知
导引:
如果1台大收割机和1台小收割机每小时各收割小麦x hm2和y hm2,那么2台大收割机和5台小收割机同时工作1 h共收割小麦_____________ hm2,3台大收割机和2台小收割机同时工作1 h共收割小麦________hm2. 由此考虑两种情况下的工作量.
探索新知
解:
设1台大收割机和1台小收割机每小时各收割小麦x hm2和y hm2. 根据两种工作方式中的相等关系,
得方程组
去括号,得
②-①,得11x=4.4.
解这个方程,得x=0.4.
把x=0.4代入①,得y=0.2.
因此,这个方程组的解是
答:1台大收割机和1台小收割机每小时各收割小麦0. 4 hm2和0. 2 hm2.
探索新知
例5 解方程组:
导引:方程①和②中x,y 的系数的绝对值都不相等,也不成
倍数关系,应取系数的绝对值的最小公倍数6,可以
先消去x,也可以先消去 y.
探索新知
解:方法一:①×3,得6x+9y=9.③
②×2,得6x+4y=22.④
③-④,得5y=-13,即
把
解得
所以这个方程组的解为
代入①,得
探索新知
方法二:①×2,得4x+6y=6.⑤
②×3,得9x+6y=33.⑥
⑥-⑤,得5x=27,解得
把
解得
所以这个方程组的解为
代入①,得
探索新知
总 结
用加减消元法解二元一次方程组时,一般有三种情况:
①方程组中某个未知数的系数的绝对值相等,则直接利用加减法求解;
②方程组中任一个未知数的系数的绝对值都不相等,但某个未知数的系数的绝对值成倍数关系,则其中一个方程乘这个倍数后再利用加减法求解;
③方程组中任一个未知数的系数的绝对值既不相等,也不成倍数关系,可利用最小公倍数的知识,把两个方程都适当地乘一个数,使某个未知数的系数的绝对值相等,然后再利用加减法求解.
探索新知
一条船顺流航行,每小时行20 km;逆流航行,每小时行16 km. 求轮船在静水中的速度与水的流速.
1
设轮船在静水中的速度为每小时x km,水的流速为每小时y km.依题意,得
①+②,得2x=36,x=18.把x=18代入①,得y=2.
所以原方程组的解为
答:轮船在静水中的速度为每小时18 km,水的流速为每小时2 km.
解:
探索新知
运输360 t化肥,装载了 6节火车车厢和15辆汽车;运输440 t化肥,装载了8节火车车厢和10辆汽车. 每节火车车厢与每辆汽车平均各装多少吨化肥?
2
设每节火车车厢平均装x t化肥,
每辆汽车平均装y t化肥.
依题意,得
解:
典题精讲
①×2,得12x+30y=720.③
②×3,得24x+30y=1 320.④
④-③,得12x=600,x=50.
把x=50代入①,得
6×50+15y=360,y=4.
所以原方程组的解为
答:每节火车车厢平均装50 t化肥,每辆汽车平均装4 t化肥.
典题精讲
若方程组 的解也是二元一次方程5x-my=-11的一个解,则m 的值等于( )
A.5
B.-7
C.-5
D.7
3
D
易错提醒
解方程组:
解:
令x+y=a,x-y=b,则原方程组可化为
解得 所以x+y=7,x-y=1,将它们组成新方程组,即 解得
所以原方程组的解是
易错点:误将换元的解当作原方程组的解(换元法)
学以致用
小试牛刀
已知x,y 满足方程组 则x+y 的值为( )
A.9
B.7
C.5
D.3
C
1
小试牛刀
用加减法解方程组 时,要使两个方程中同一未知数的系数相等或相反,有以下四种变形的结果:
其中变形正确的是( )
A.①② B.③④ C.①③ D.②④
B
2
小试牛刀
小明在某商店购买商品A,B 共两次,这两次购买商品A,B的数量和费用如表:
购买商品A的数量/个 购买商品B 的数量/个 购买总
费用/元
第一次购物 4 3 93
第二次购物 6 6 162
若小丽需要购买3个商品A 和2个商品B,则她要花费( )
A.64元 B.65元 C.66元 D.67元
C
3
小试牛刀
选择适当的方法解方程组.
(1)
将①代入②,得2y+9=11,所以y=1.
将y=1代入①,得x-1=3. 所以x=4.
所以原方程组的解为
解:
4
小试牛刀
①×10-②,得25y=10,所以y= .
将y= 代入②,得5x-5× =-4,所以x=0.
所以原方程组的解是
小试牛刀
阅读下列内容,回答问题:
解方程组时,有时可根据方程的未知数的系数特征,将几个方程直接进行整体加减.如解方程组
①+②,得10x+10y=30,
即x+y=3,③
将①变形为3x+3y+5y=14,即3(x+y)+5y=14.④
把③代入④,得3×3+5y=14,求得y=1,
再把y=1代入③,得x=3-1,即x=2.
5
小试牛刀
从而比较简便地求得原方程组的解为
上述这种方法我们称它为“整体加减法”,你若留心观察,
有很多方程组都可采用此法解,请你用这种方法解方程
组
小试牛刀
①+②,得4 035x+4 035y=4 035,x+y=1.③
将①变形为2 017x+2 017y+y=2 016,
即2 017(x+y )+y=2 016,④
将③代入④,得2 017×1+y=2 016,解得y=-1.
再将y=-1代入③,得x=2.
所以原方程组的解为
解:
小试牛刀
解方程组 时,若设 =m, =n,则原方程组可
变形为关于m,n 的方程组
解这个方程组得到它的解为
由 =5, =-4,求得原方程组的解为利用上述方法
解方程组:
6
小试牛刀
设 =m, =n,
则原方程组可变形为
解这个方程组得到它的解为
由 =3, =-2,
求得原方程组的解为
解:
小试牛刀
已知关于x,y 的二元一次方程组
的解互为相反数,求k 的值.
解方程组 得
由关于x,y 的二元一次方程组 的解
互为相反数,可得2k+3-2-k=0,解得k=-1.
解:
7
小试牛刀
小明想从“天猫”某网店购买计算器,经查询,某品牌A型号计算器的单价比B型号计算器的单价多10元,5台A型号的计算器与7台B型号的计算器的价钱相同,问A,B两种型号计算器的单价分别是多少?
设A型号计算器的单价为x 元,B型号计算器的单价
为y元,依题意,得 解得
答:A型号计算器的单价为35元,B型号计算器的单价为25元.
解:
8
小试牛刀
如图①,在3×3的方格中,填写了一些整式,使得每行3个数、每列3个数、对角线上3个数的和均相等.
(1)求x,y 的值;
(2)根据求得的x,y,a,b,c 的值完成图②.
9
小试牛刀
(1)由题意,得
解得
(2)由(1)知x=-1,所以3+4+x=6,
所以 解得
如图.
解:
3 4 -1
-2 2 6
5 0 1
小试牛刀
请根据图中提供的信息,回答下列问题:
(1)一个暖瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的暖瓶和水杯.为了迎接新年,两家商场都在搞促销活动.甲商场规定:这两种商品都打九折;乙商场规定:买一个暖瓶赠送一个水杯.若某单位想要买4个暖瓶和15个水杯,请问选择哪家商场购买更合算?并说明理由.
10
小试牛刀
(1)设一个暖瓶与一个水杯分别为x 元、y 元,
由题意,得 解得
所以一个暖瓶与一个水杯分别为30元、8元.
(2)在乙商场购买更合算.理由:若该单位在甲商场购买,则需钱数为4×30×0.9+15×8×0.9=216(元);若在乙商场购买,则需钱数为4×30+(15-4)×8=208(元).所以在乙商场购买更合算.
解:
课堂小结
课堂小结
用加减消元法解二元一次方程组的一般步骤:
(1)变形:将方程组中某一未知数的系数变为相等或相反.
(2)加减:消去一个未知数.
(3)求解:得到一个未知数的值.
(4)回代:求另一个未知数的值.
(5)写出解.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
