【班海精品】人教版(新)七下-9.1 不等式 第一课时【优质课件】
文档属性
| 名称 | 【班海精品】人教版(新)七下-9.1 不等式 第一课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 8.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 10:20:52 | ||
图片预览











文档简介
(共47张PPT)
9.1 不 等 式
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
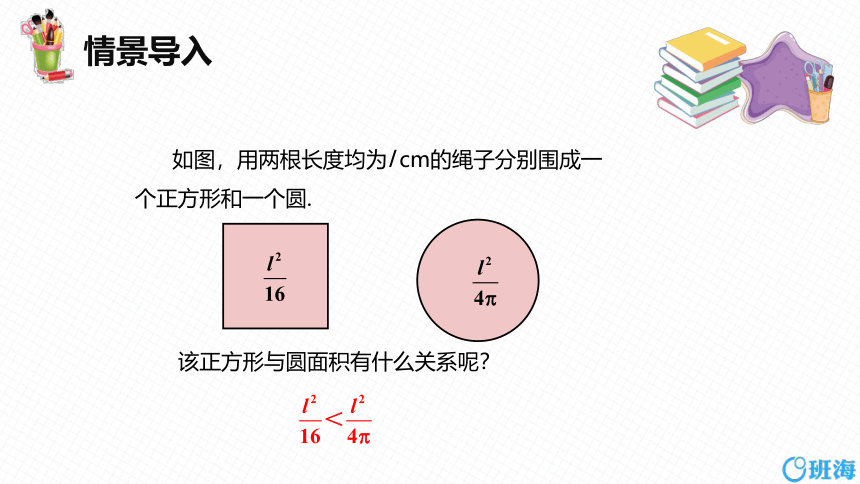
如图,用两根长度均为l cm的绳子分别围成一
个正方形和一个圆.
该正方形与圆面积有什么关系呢?
新课精讲
探索新知
1
知识点
不等式的定义
问题 一辆匀速行驶的汽车在11:20距离A 地50 km,要在12:00之前驶过A地,车速应满足什么条件?
设车速是 x km/h.
从时间上看,汽车要在12:00之前驶过A地,
则以这个速度行驶50 km所用的时间不到 h,
即
分析:
探索新知
从路程上看,汽车要在12:00之前驶过A地,则
以这个速度行驶 h的 路程要超过50 km,即
式子①和②从不同角度表示了车速应满足的条件.
探索新知
归 纳
像①和②这样用符号“<”或“>”表示大小关
系的式子,叫做不等式 . 像a+2≠a-2这样用符号
“≠”表示不等关系的式子也是不等式 .
探索新知
不等式的分类(按条件分):
(1)绝对不等式:任何条件下都成立的不等式,如
a2+1>0;
(2)矛盾不等式:任何条件下都不成立的不等式,如
a2+1<0;
(3)条件不等式:在一定条件下才能成立的不等式
(主要研究的不等式).
探索新知
下列式子是不等式的有( )
①2x=20;②3>2;③x≠4-3;④5a+6b ;
⑤ x>2y;⑥1≤3x+5y;⑦ ;⑧ >3.
A.2个 B.3个 C.4个 D.5个
例1
导引:
判断一个式子是否为不等式的关键在于式子中是
否含有“≠”“>”“<”“≥”“≤”,由此可
知②③⑤⑥⑧是不等式.
D
探索新知
总 结
一个式子是不等式,要把握两点:
一是含有不等号;
二是表示不等关系,而与不等式是否成立无关.
典题精讲
1
用“<”或“>”号填空.
(1)-2____2; (2)-3____-2;
(3)12____6; (4)0____-8;
(5)-a____a (a>0); (6)-a____a(a<0).
<
<
>
>
<
>
典题精讲
2
下列式子:①-2<0;②4x+2y≥0;
③x=1;④x2-xy;⑤x≠3;⑥x-1<y+2. 其中不等式有( )
A.5个 B.4个
C.3个 D.2个
B
探索新知
2
知识点
用不等式表示数量关系
列不等式的一般步骤是:
(1)分析题意,找出题目中的各种量;
(2)寻找各种量之间的不等关系;
(3)用代数式表示各量;
(4)用适当的符号将各量连接起来.
探索新知
列不等式:
(1)a 与1的和是正数:____________;
(2)a 与3的和小于-3:____________;
(3)a 与-2的差大于5:____________;
(4)a 的5倍小于10:____________;
(5)a 的三分之一大于-7:____________.
例2
根据题中语言的叙述体现的数量关系列出式子,
然后结合体现不等关系的关键字眼列出不等式.
导引:
a+1>0
a+3<-3
a-(-2)>5
5a<10
a>-7
探索新知
总 结
列不等式首先要找出表示不等关系的关键词,然后用表示数量关系的式子表示不等式的左边和右边.
典题精讲
1
用不等式表示:
(1) a 是正数; (2) a 是负数;
(3) a 与5的和小于7; (4) a 与2的差大于-1;
(5) a 的4倍大于8; (6) a 的一半小于3.
(1)a>0;(2)a<0;(3)a+5<7;(4)a-2>-1;(5)4a>8;(6) a<3.
解:
典题精讲
2
下列数量关系用不等式表示错误的是( )
A.若a 是负数,则a<0
B.若m 的值小于1,则m<1
C.若x 与-1的和大于0,则x-1>0
D.若a 的 大于b,则 a≠b
D
典题精讲
3
如图,A,B 两点在数轴上表示的数分别为a,b,下列式子成立的是( )
A.ab>0
B.a+b<0
C.(b-1)(a+1)>0
D.(b-1)(a-1)>0
C
探索新知
3
知识点
不等式的解与解集
1.不等式的解:能使不等式成立的未知数的值,
叫做不等式的解.
2.不等式的解集:一个含有未知数的不等式的
所有解,组成这个不等式的解集.
3.求不等式解集的过程叫做解不等式.
探索新知
下列说法中,正确的是( )
A. x=-3是不等式x+4<1的解
B. x> 是不等式-2x>-3的解集
C.不等式x>-5的负整数解有无数多个
D.不等式x<7的非正整数解有无数多个
例3
D
探索新知
导引:
当x=-3时,x+4=-3+4=1,所以A错;取
一个能使不等式x> 成立的值,如x=2,代
入不等式-2x>-3,发现不等式-2x>-3不
成立,故x=2不是-2x>-3的解,所以x>
不是不等式-2x>-3的解集,故B错;不等式
x>-5的负整数解只有-1,-2,-3,-4,
共4个,所以C错.
探索新知
总 结
判断一个数值是不是不等式的解,只需代入验证即可.由于不等式的解集必须符合两个条件:
(1)解集中的每一个数值都能使不等式成立;
(2)能够使不等式成立的所有数值都在解集中,因此如果解集内有一个数能够使不等式不成立或解集外有一个数能够使不等式成立,那么这个解集就不是这个不等式的解集.
典题精讲
1
下列数中哪些是不等式x+3>6的解?哪些不是?
-4,-2.5,0,1,2.5,3,3.2,4.8,8,12.
3.2,4.8,8,12是不等式x+3>6的解;
-4,-2.5,0,1,2.5,3不是不等式x+3>6的解.
解:
典题精讲
2
直接说出下列不等式的解集:
(1) x+3>6;(2) 2x<8;(3) x-2>0.
(1) x>3;
(2) x<4;
(3) x>2.
解:
典题精讲
不等式x≤3.5的正整数解是 ;不等式x≥-3.5的整数解有________个,其中小于1的整数解有 .
3
1, 2, 3
无数
-3,-2,-1,0
下列说法中,错误的是( )
A.不等式x<5的整数解有无数个
B.不等式x>-5的负数解有有限个
C.不等式x+4>0的解集是x>-4
D.x=-40是不等式2x<-8的一个解
4
B
探索新知
4
知识点
不等式解集在数轴上的表示法
议一议
请你用自己的方式将不等式x>5的解集和不等式
x-5≤-1的解集分别表示在数轴上,并与同伴交流.
探索新知
归 纳
不等式x>5的解集可以用数轴上表示5的点的
右边部分来表示(如图)在数轴上表示5的点的位
置上画空心圆圈,表示5不在这个解集内.
探索新知
不等式x-5≤-1的解集x≤4可以用数轴上表
示4的点及其左边部分来表示(如图),在数轴上表
示4的点的位置上画实心圆点,表示4在这个解集内.
归 纳
探索新知
不等式的解集在数轴上的表示方法:
注意:
若不等号是“≥”或“≤”,则边界点为实心圆点;若不等号是“>”或“<”,则边界点为空心圆圈.
探索新知
在数轴上表示下列不等式的解集:
(1)x>2; (2)x≤3; (3)x<-1; (4)x≥1.
例4
分析:
先画数轴,再定界点,最后定方向.
如图所示.
解:
探索新知
总 结
(1)在定方向时,要注意不要搞错方向,大于向右.小于向左.
(2)有等于号(≤,≥)画实心圆点,无等于号(<,>)画空心圆圈.
(3)在数轴上表示不等式的解集,一般分三步:画数轴,定界点,定方向.
典题精讲
1
在数轴上表示不等式x-1<0的解集,正确的是( )
C
典题精讲
2
某个关于x的不等式的解集在数轴上表示如图,则该解集是( )
A.-2<x<3 B.-2<x≤3
C.-2≤x<3 D.-2≤x≤3
B
易错提醒
“满足x<2的每一个数都是不等式x+2<5的解,所以不等式x+2<5的解集是x<2,”这句话是否正确,请你判断,并说明理由.
解:
不正确.因为x+2<5的解集是x<3,即凡是小于3的数都是不等式x+2<5的解,所以满足x<2的数只是x+2<5的部分解,故x<2不是其解集.
易错点:对不等式的解集的意义理解不透而出错
学以致用
小试牛刀
某市某天的最高气温是33 ℃,最低气温是24 ℃,则该市这一天的气温t (℃)的变化范围是( )
A.t>33
B.t≤24
C.24<t<33
D.24≤t≤33
D
1
小试牛刀
下列说法中正确的是( )
A.x=1是方程-2x=2的解
B.x=-1是不等式-2x >2的唯一解
C.x=-2是不等式-2x >2的解集
D.x=-2,-3都是不等式-2x >2的解且它的解有无数个
D
2
小试牛刀
3
已用不等式表示:
(1)a 的一半与3的和大于5;
(2)X 的3倍与1的差小于2;
(3)a 的 与1的差是正数;
(4)m 与2的差是负数.
(1) a+3>5. (2)3x-1<2.
(3) a-1>0. (4)m-2<0.
解:
小试牛刀
4
已知a<x≤b 的整数解为5,6,7.
(1)当a,b 为整数时,求a,b 的值;
(2)当a,b 为实数时,求a,b 的取值范围.
(1)a=4,b=7. (2)4≤a<5,7≤b<8.
解:
小试牛刀
5
已用甲、乙两种原料配制成某种饮料,已知这两种原料的维生素C的含量及购买这两种原料的价格如下表:
(1)现配制这种饮料9 kg,要求至少含有4 000单位的维生素C,试写出所需甲种原料的质量x (kg)应满足的不等式;
(2)如果还要求甲、乙两种原料的费用不超过70元,试写出
x (kg)应满足的另一个不等式.
原料 甲种原料 乙种原料
维生素C含量(单位/kg) 500 80
原料价格(元/kg) 16 4
小试牛刀
(1)由题意,得500x+80×(9-x)≥4 000.
(2)由题意,得16x+4×(9-x)≤70.
解:
阅读下列材料,并完成下列各题.
你能比较2 0182 019和2 0192 018的大小吗?
为了解决这个问题,先把问题一般化,比较nn+1和(n+1)n(n≥1,且n为整数)的大小.然后从分析n=1,n=2,n=3,…的简单情形入手,从中发现规律,经过归纳、猜想得出结论.
(1)通过计算(可用计算器)比较下列①~⑦组两数的大小;(在横线上填上“>”“=”或“<”)
①12____21;②23____32;③34____43;④45____54;
小试牛刀
6
<
<
>
>
小试牛刀
7
⑤56____65;⑥67____76;⑦78____87.
(2)归纳第(1)问的结果,猜想出nn+1和(n+1)n的大小关系.
(3)根据以上结论,请判断2 0182 019和2 0192 018的大小关系.
>
>
>
(2)当n=1或2时,nn+1<(n+1)n;
当n≥3时,nn+1>(n+1)n.
(3)2 0182 019>2 0192 018.
解:
课堂小结
课堂小结
知识方法要点 关键总结 注意事项
不等式的概念 表示不等关系的式子 注意“不大于”“不小于”的含义
列不等式 理清要比较的两个量;正确使用不等号 弄清题意,抓住关键词
不等式的解 能使不等式成立的未知数的值 指未知数的某个值
不等式的解集 一个含未知数的不等式的所有解 解集中包含了每一个不等式的解
不等式解集的表示方法 ①用简单的不等式表示;②用数轴表示
界点和方向
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
9.1 不 等 式
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
如图,用两根长度均为l cm的绳子分别围成一
个正方形和一个圆.
该正方形与圆面积有什么关系呢?
新课精讲
探索新知
1
知识点
不等式的定义
问题 一辆匀速行驶的汽车在11:20距离A 地50 km,要在12:00之前驶过A地,车速应满足什么条件?
设车速是 x km/h.
从时间上看,汽车要在12:00之前驶过A地,
则以这个速度行驶50 km所用的时间不到 h,
即
分析:
探索新知
从路程上看,汽车要在12:00之前驶过A地,则
以这个速度行驶 h的 路程要超过50 km,即
式子①和②从不同角度表示了车速应满足的条件.
探索新知
归 纳
像①和②这样用符号“<”或“>”表示大小关
系的式子,叫做不等式 . 像a+2≠a-2这样用符号
“≠”表示不等关系的式子也是不等式 .
探索新知
不等式的分类(按条件分):
(1)绝对不等式:任何条件下都成立的不等式,如
a2+1>0;
(2)矛盾不等式:任何条件下都不成立的不等式,如
a2+1<0;
(3)条件不等式:在一定条件下才能成立的不等式
(主要研究的不等式).
探索新知
下列式子是不等式的有( )
①2x=20;②3>2;③x≠4-3;④5a+6b ;
⑤ x>2y;⑥1≤3x+5y;⑦ ;⑧ >3.
A.2个 B.3个 C.4个 D.5个
例1
导引:
判断一个式子是否为不等式的关键在于式子中是
否含有“≠”“>”“<”“≥”“≤”,由此可
知②③⑤⑥⑧是不等式.
D
探索新知
总 结
一个式子是不等式,要把握两点:
一是含有不等号;
二是表示不等关系,而与不等式是否成立无关.
典题精讲
1
用“<”或“>”号填空.
(1)-2____2; (2)-3____-2;
(3)12____6; (4)0____-8;
(5)-a____a (a>0); (6)-a____a(a<0).
<
<
>
>
<
>
典题精讲
2
下列式子:①-2<0;②4x+2y≥0;
③x=1;④x2-xy;⑤x≠3;⑥x-1<y+2. 其中不等式有( )
A.5个 B.4个
C.3个 D.2个
B
探索新知
2
知识点
用不等式表示数量关系
列不等式的一般步骤是:
(1)分析题意,找出题目中的各种量;
(2)寻找各种量之间的不等关系;
(3)用代数式表示各量;
(4)用适当的符号将各量连接起来.
探索新知
列不等式:
(1)a 与1的和是正数:____________;
(2)a 与3的和小于-3:____________;
(3)a 与-2的差大于5:____________;
(4)a 的5倍小于10:____________;
(5)a 的三分之一大于-7:____________.
例2
根据题中语言的叙述体现的数量关系列出式子,
然后结合体现不等关系的关键字眼列出不等式.
导引:
a+1>0
a+3<-3
a-(-2)>5
5a<10
a>-7
探索新知
总 结
列不等式首先要找出表示不等关系的关键词,然后用表示数量关系的式子表示不等式的左边和右边.
典题精讲
1
用不等式表示:
(1) a 是正数; (2) a 是负数;
(3) a 与5的和小于7; (4) a 与2的差大于-1;
(5) a 的4倍大于8; (6) a 的一半小于3.
(1)a>0;(2)a<0;(3)a+5<7;(4)a-2>-1;(5)4a>8;(6) a<3.
解:
典题精讲
2
下列数量关系用不等式表示错误的是( )
A.若a 是负数,则a<0
B.若m 的值小于1,则m<1
C.若x 与-1的和大于0,则x-1>0
D.若a 的 大于b,则 a≠b
D
典题精讲
3
如图,A,B 两点在数轴上表示的数分别为a,b,下列式子成立的是( )
A.ab>0
B.a+b<0
C.(b-1)(a+1)>0
D.(b-1)(a-1)>0
C
探索新知
3
知识点
不等式的解与解集
1.不等式的解:能使不等式成立的未知数的值,
叫做不等式的解.
2.不等式的解集:一个含有未知数的不等式的
所有解,组成这个不等式的解集.
3.求不等式解集的过程叫做解不等式.
探索新知
下列说法中,正确的是( )
A. x=-3是不等式x+4<1的解
B. x> 是不等式-2x>-3的解集
C.不等式x>-5的负整数解有无数多个
D.不等式x<7的非正整数解有无数多个
例3
D
探索新知
导引:
当x=-3时,x+4=-3+4=1,所以A错;取
一个能使不等式x> 成立的值,如x=2,代
入不等式-2x>-3,发现不等式-2x>-3不
成立,故x=2不是-2x>-3的解,所以x>
不是不等式-2x>-3的解集,故B错;不等式
x>-5的负整数解只有-1,-2,-3,-4,
共4个,所以C错.
探索新知
总 结
判断一个数值是不是不等式的解,只需代入验证即可.由于不等式的解集必须符合两个条件:
(1)解集中的每一个数值都能使不等式成立;
(2)能够使不等式成立的所有数值都在解集中,因此如果解集内有一个数能够使不等式不成立或解集外有一个数能够使不等式成立,那么这个解集就不是这个不等式的解集.
典题精讲
1
下列数中哪些是不等式x+3>6的解?哪些不是?
-4,-2.5,0,1,2.5,3,3.2,4.8,8,12.
3.2,4.8,8,12是不等式x+3>6的解;
-4,-2.5,0,1,2.5,3不是不等式x+3>6的解.
解:
典题精讲
2
直接说出下列不等式的解集:
(1) x+3>6;(2) 2x<8;(3) x-2>0.
(1) x>3;
(2) x<4;
(3) x>2.
解:
典题精讲
不等式x≤3.5的正整数解是 ;不等式x≥-3.5的整数解有________个,其中小于1的整数解有 .
3
1, 2, 3
无数
-3,-2,-1,0
下列说法中,错误的是( )
A.不等式x<5的整数解有无数个
B.不等式x>-5的负数解有有限个
C.不等式x+4>0的解集是x>-4
D.x=-40是不等式2x<-8的一个解
4
B
探索新知
4
知识点
不等式解集在数轴上的表示法
议一议
请你用自己的方式将不等式x>5的解集和不等式
x-5≤-1的解集分别表示在数轴上,并与同伴交流.
探索新知
归 纳
不等式x>5的解集可以用数轴上表示5的点的
右边部分来表示(如图)在数轴上表示5的点的位
置上画空心圆圈,表示5不在这个解集内.
探索新知
不等式x-5≤-1的解集x≤4可以用数轴上表
示4的点及其左边部分来表示(如图),在数轴上表
示4的点的位置上画实心圆点,表示4在这个解集内.
归 纳
探索新知
不等式的解集在数轴上的表示方法:
注意:
若不等号是“≥”或“≤”,则边界点为实心圆点;若不等号是“>”或“<”,则边界点为空心圆圈.
探索新知
在数轴上表示下列不等式的解集:
(1)x>2; (2)x≤3; (3)x<-1; (4)x≥1.
例4
分析:
先画数轴,再定界点,最后定方向.
如图所示.
解:
探索新知
总 结
(1)在定方向时,要注意不要搞错方向,大于向右.小于向左.
(2)有等于号(≤,≥)画实心圆点,无等于号(<,>)画空心圆圈.
(3)在数轴上表示不等式的解集,一般分三步:画数轴,定界点,定方向.
典题精讲
1
在数轴上表示不等式x-1<0的解集,正确的是( )
C
典题精讲
2
某个关于x的不等式的解集在数轴上表示如图,则该解集是( )
A.-2<x<3 B.-2<x≤3
C.-2≤x<3 D.-2≤x≤3
B
易错提醒
“满足x<2的每一个数都是不等式x+2<5的解,所以不等式x+2<5的解集是x<2,”这句话是否正确,请你判断,并说明理由.
解:
不正确.因为x+2<5的解集是x<3,即凡是小于3的数都是不等式x+2<5的解,所以满足x<2的数只是x+2<5的部分解,故x<2不是其解集.
易错点:对不等式的解集的意义理解不透而出错
学以致用
小试牛刀
某市某天的最高气温是33 ℃,最低气温是24 ℃,则该市这一天的气温t (℃)的变化范围是( )
A.t>33
B.t≤24
C.24<t<33
D.24≤t≤33
D
1
小试牛刀
下列说法中正确的是( )
A.x=1是方程-2x=2的解
B.x=-1是不等式-2x >2的唯一解
C.x=-2是不等式-2x >2的解集
D.x=-2,-3都是不等式-2x >2的解且它的解有无数个
D
2
小试牛刀
3
已用不等式表示:
(1)a 的一半与3的和大于5;
(2)X 的3倍与1的差小于2;
(3)a 的 与1的差是正数;
(4)m 与2的差是负数.
(1) a+3>5. (2)3x-1<2.
(3) a-1>0. (4)m-2<0.
解:
小试牛刀
4
已知a<x≤b 的整数解为5,6,7.
(1)当a,b 为整数时,求a,b 的值;
(2)当a,b 为实数时,求a,b 的取值范围.
(1)a=4,b=7. (2)4≤a<5,7≤b<8.
解:
小试牛刀
5
已用甲、乙两种原料配制成某种饮料,已知这两种原料的维生素C的含量及购买这两种原料的价格如下表:
(1)现配制这种饮料9 kg,要求至少含有4 000单位的维生素C,试写出所需甲种原料的质量x (kg)应满足的不等式;
(2)如果还要求甲、乙两种原料的费用不超过70元,试写出
x (kg)应满足的另一个不等式.
原料 甲种原料 乙种原料
维生素C含量(单位/kg) 500 80
原料价格(元/kg) 16 4
小试牛刀
(1)由题意,得500x+80×(9-x)≥4 000.
(2)由题意,得16x+4×(9-x)≤70.
解:
阅读下列材料,并完成下列各题.
你能比较2 0182 019和2 0192 018的大小吗?
为了解决这个问题,先把问题一般化,比较nn+1和(n+1)n(n≥1,且n为整数)的大小.然后从分析n=1,n=2,n=3,…的简单情形入手,从中发现规律,经过归纳、猜想得出结论.
(1)通过计算(可用计算器)比较下列①~⑦组两数的大小;(在横线上填上“>”“=”或“<”)
①12____21;②23____32;③34____43;④45____54;
小试牛刀
6
<
<
>
>
小试牛刀
7
⑤56____65;⑥67____76;⑦78____87.
(2)归纳第(1)问的结果,猜想出nn+1和(n+1)n的大小关系.
(3)根据以上结论,请判断2 0182 019和2 0192 018的大小关系.
>
>
>
(2)当n=1或2时,nn+1<(n+1)n;
当n≥3时,nn+1>(n+1)n.
(3)2 0182 019>2 0192 018.
解:
课堂小结
课堂小结
知识方法要点 关键总结 注意事项
不等式的概念 表示不等关系的式子 注意“不大于”“不小于”的含义
列不等式 理清要比较的两个量;正确使用不等号 弄清题意,抓住关键词
不等式的解 能使不等式成立的未知数的值 指未知数的某个值
不等式的解集 一个含未知数的不等式的所有解 解集中包含了每一个不等式的解
不等式解集的表示方法 ①用简单的不等式表示;②用数轴表示
界点和方向
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
