【班海精品】人教版(新)七下-6.1 平方根 第三课时【优质课件】
文档属性
| 名称 | 【班海精品】人教版(新)七下-6.1 平方根 第三课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 10.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 10:20:43 | ||
图片预览











文档简介
(共49张PPT)
6.1 平 方 根
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
想一想
(1)9的算术平方根是3,也就是说,3的平方是9.
还有其他的数,它的平方也是9吗?
(2)平方等于 的数有几个?平方等于0.64
的数呢?
新课精讲
探索新知
1
知识点
平方根的定义
一般地,如果一个数x的平方等于a,即x 2 =
a,那么这个数x 就叫做a 的平方根(也叫做二
次方根) .
如:±3是9的平方根, 或说成9的平方根是±3.
探索新知
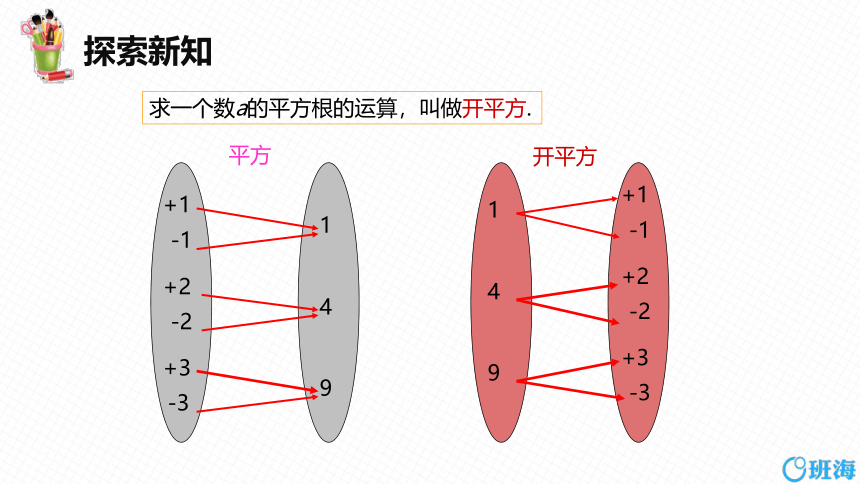
求一个数a的平方根的运算,叫做开平方.
1
4
9
+1
-1
+2
-2
+3
-3
1
4
9
+1
-1
+2
-2
+3
-3
开平方
平方
探索新知
下列说法中正确的是( )
A.9的平方根是±3,应表示为92=±3
B.±3是9的平方根,应表示为± =3
C.9开平方能得到9的平方根,即 =±3
D.9的算术平方根是3,应表示为 =3
例1
导引:
正确把握并准确运用平方根、算术平方根的定义.
D
探索新知
总 结
必须弄清以下符号的意义:± (a≥0)表示非负数a
的平方根, (a≥0)表示非负数a 的算术平方根,把非负
数a 开平方,它的平方根可用± 表示.
典题精讲
1
平方根概念的起源与几何中的正方形有关. 如果一个正方形的面积为A,那么 这个正方形的边长是多少?.
解:
正方形的面积是边长的平方,根据算术平方根的定义可得:正方形的边长是 (A>0).
典题精讲
2
如果x 2=a,那么下列说法错误的是( )
A. 若x 确定,则a 的值是唯一的
B. 若a 确定,则x 的值是唯一的
C. a 是x 的平方
D. x 是a 的平方根
B
典题精讲
3
4的平方根是( )
A.16 B.2
C.±2 D.±
C
探索新知
议一议
(1)一个正数有几个平方根?
(2)0有几个平方根?
(3)负数呢?
2
知识点
平方根的性质
探索新知
平方根的性质
(1)平方根的性质:
一个正数有两个平方根;0只有一个平方
根,它是0本身;负数没有平方根.
(2)平方根的表示方法:
正数a有两个平方根,一个是a 的算术平
方根 ,另一个是 ,它们互为相反
数.这两个平方根合起来可以记作
读作“正、负根号a”.
探索新知
求下列各式的值:
(1) ; (2) ; (3) .
例2
解:
(1)因为62=36,所以 =6;
(2)因为0.92=0.81,所以 ;
(3)因为 ,所以 .
典题精讲
总 结
求一个式子的值,先分析式子的意义,特别是看清它表示的是算术平方根还是平方根,就是看清符号,最后的结果不改变它的正负性.
典题精讲
1
判断下列说法是否正确:
(1) 0的平方根是0;
(2) 1的平方根是1;
(3) -1的平方根是-1;
(4) 0.01是0.1的一个平方根.
解:
(1)正确;(2)错误;(3)错误;(4)错误.
典题精讲
2
下列说法正确的是( )
A.任何数的平方根都有两个
B.一个正数的平方根的平方就是这个数
C.负数也有平方根
D.非负数的平方根都有两个
B
典题精讲
3
下列说法正确的有( )
①-2是-4的一个平方根;
②a2的平方根是a;
③2是4的一个平方根;
④4的平方根是-2.
A.1个 B.2个
C.3个 D.4个
A
典题精讲
4
下列关于“0”的说法中,正确的是( )
A.0是最小的正整数
B.0没有相反数
C.0没有倒数
D.0没有平方根
C
探索新知
3
知识点
求平方根(开平方)
1.开平方:
求一个数a 的平方根的运算,叫做开平方, a 叫做被开方数.
2.要点精析:
(1)一个正数的正的平方根就是它的算术平方根.
(2)平方与开平方是互逆运算.开平方与加、减、乘、除、乘方
一样是一种运算,即:
运算名称:加、减、乘、除、乘方、开平方(非负数).
运算结果:和、差、积、商、幂、平方根(互为相反数).
探索新知
求下列各数的平方根:
(1) 100; (2) ; (3) 0.25.
例3
解:
(1)因为(±10)2=100,所以100的平方根是±10;
(2)因为 ,所以 的平方根是
(3)因为(±0.5)2=0.25,所以0.25的平方根是±0.5.
探索新知
总 结
要从根本之处理解一个数的平方根的运算,从平
方根的概念入手,同时要知道,只有非负数才有平方
根.同时注意平方根的通用符号是 (a≥0),防止粗
心大意漏掉“ ”而出错.
典题精讲
x 8 -8
x2 16 0.36 1
填表:
64
4
-4
0.6
-0.6
典题精讲
2
计算下列各式的值:
(1) ; (2) ; (3) .
解:
(3)因为 ,所以 .
典题精讲
3
的平方根是( )
A.± B.
C.± D.
C
4
│1+ │+│1- │ =( )
A.1 B.
C.2 D.2
D
探索新知
4
知识点
与 的性质
1.想一想:
(1) 等于多少? 等于多少?
(2) 等于多少?
(3)对于正数a, 等于多少?
2.联系拓广:
对于任意数a, 一定等于a 吗?
探索新知
1. 的化简:
2. 的化简:
典题精讲
下列结论正确的是( )
A.- =-6 B .(- )2=9
C. =±16 D.
1
A
典题精讲
下列四个数中,是负数的是( )
A. |-2| B.(-2)2
C. D.
2
C
易错提醒
下列说法不正确的是( )
A.21的平方根是±
B. 是21的一个平方根
C. 是21的算术平方根
D.21的平方根是
D
易错点:混淆平方根与算术平方根的概念而出错.
学以致用
小试牛刀
“± ”的意义是( )
A.a 的平方根
B.a 的算术平方根
C.当a≥0时,± 是a 的平方根
D.以上均不正确
C
1
小试牛刀
下列说法正确的是( )
A.|-2|=-2
B.0的倒数是0
C.4的平方根是2
D.-3的相反数是3
D
2
小试牛刀
若2m-4与3m-1是同一个数的平方根,则m的值是( )
A.-3 B.-1
C.1 D.-3或1
3
D
小试牛刀
实数a,b在数轴上对应的点的位置如图所示,化简|a|+ 的结果是( )
A.-2a+b B.2a-b
C.-b D.b
A
4
小试牛刀
求下列各数的平方根和算术平方根:
(1)225; (2) ; (3) ;(4)0.003
(1)因为(±15)2=225,所以225的平方根是±15.
因为152=225,所以225的算术平方根是15.
(2) .因为 ,
所以 的平方根是± .
因为 ,所以 的算术平方根是 .
解:
5
(3)因为 ,
所以 的平方根是±1 .
因为 ,
所以 的算术平方根是1 .
(4)因为(±0.06)2=0.003 6,所以0.003 6的平方根是±0.06.
因为0.062=0.003 6,所以0.003 6的算术平方根是0.06.
小试牛刀
小试牛刀
由(2x+1)2-121=0,得(2x+1)2=121,
所以2x+1=±11.即2x+1=11或2x+1=-11,
解得x=5或x=-6.
已知(2x+1)2-121=0,求x 的值.
解:
6
小试牛刀
解:
已知一个正数的两个平方根分别是2m+1和5-3m,求m 的值和这个正数.
因为一个正数的两个平方根互为相反数,
所以(2m+1)+(5-3m)=0,解得m=6.
此时2m+1=2×6+1=13,
5-3m=5-3×6=-13.
因为(±13)2=169,所以这个正数是169.
7
小试牛刀
已知2m+3和4m+9是一个正数的平方根,求m 的值
和这个正数的平方根.
分两种情况进行讨论:
(1)当2m+3≠4m+9时,得(2m+3)+(4m+9)=0,
解得m=-2.所以2m+3=2×(-2)+3=-1,
4m+9=4×(-2)+9=1.
所以这个正数的平方根是±1.
(2)当2m+3=4m+9时,得m=-3,
此时这个正数为(2m+3)2=9.
所以这个正数的平方根为±3.
解:
8
小试牛刀
已知2m+2的平方根是±4,3m+n+1的平方根是
±5,求m+2n的值.
由题意,得2m+2=(±4)2=16,
3m+n+1=(±5)2=25,解得m=7,n=3.
所以m+2n=7+2×3=13.
解:
9
小试牛刀
阅读下列材料:
当a>0时,如a=6,则|a|=|6|=6,故此时a 的绝对值是它本身;
当a=0时,|a|=|0|=0,故此时a 的绝对值是0;
当a<0时,如a=-6,则|a|=|-6|=-(-6),故此时a 的绝
对值是它的相反数.
综上可知,
|a|=
这种分析方法渗透了数学中的分类讨论思想.
10
小试牛刀
回答下列问题:
(1)请仿照材料中的分类讨论思想,分析 的情况;
(2)猜想 与|a|的大小关系.
(1)当a>0时,如a=5,则 =5,故此时 =a;
当a=0时, =0;当a<0时,如a=-5,
则 =-(-5),故此时 =-a.
综上可知, =
(2) =|a|.
解:
11
小试牛刀
已知a,b,c 在数轴上对应点的位置如图所示,
化简 .
解:
由a,b,c在数轴上对应点的位置可知a<0,
a+b<0,c-a>0,b+c<0,
所以原式=|a|-|a+b|+(c-a)+|b+c|
=-a+(a+b)+c-a-(b+c)
=-a+a+b+c-a-b-c
=-a.
12
课堂小结
课堂小结
1. 定义:若x2=a,则x 叫做a 的平方根.
2. 性质:一个正数有两个平方根,它们互为相反数,
0的平方根是0,负数没有平方根.
3. 平方根与开平方间的关系:
(1)开平方是求平方根的运算;
(2)平方根是开平方运算的结果.
课堂小结
求一个非负数的平方根的方法:
① 求一个非负数a 的平方根,就是要把平方后等于a 的
数找出来,从而求出a 的所有平方根;
② 求带分数的平方根时,应先将带分数化为假分数,
这也是常出错的地方.
注意:正数的平方根有两个,前面必定有“±”号.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
6.1 平 方 根
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
想一想
(1)9的算术平方根是3,也就是说,3的平方是9.
还有其他的数,它的平方也是9吗?
(2)平方等于 的数有几个?平方等于0.64
的数呢?
新课精讲
探索新知
1
知识点
平方根的定义
一般地,如果一个数x的平方等于a,即x 2 =
a,那么这个数x 就叫做a 的平方根(也叫做二
次方根) .
如:±3是9的平方根, 或说成9的平方根是±3.
探索新知
求一个数a的平方根的运算,叫做开平方.
1
4
9
+1
-1
+2
-2
+3
-3
1
4
9
+1
-1
+2
-2
+3
-3
开平方
平方
探索新知
下列说法中正确的是( )
A.9的平方根是±3,应表示为92=±3
B.±3是9的平方根,应表示为± =3
C.9开平方能得到9的平方根,即 =±3
D.9的算术平方根是3,应表示为 =3
例1
导引:
正确把握并准确运用平方根、算术平方根的定义.
D
探索新知
总 结
必须弄清以下符号的意义:± (a≥0)表示非负数a
的平方根, (a≥0)表示非负数a 的算术平方根,把非负
数a 开平方,它的平方根可用± 表示.
典题精讲
1
平方根概念的起源与几何中的正方形有关. 如果一个正方形的面积为A,那么 这个正方形的边长是多少?.
解:
正方形的面积是边长的平方,根据算术平方根的定义可得:正方形的边长是 (A>0).
典题精讲
2
如果x 2=a,那么下列说法错误的是( )
A. 若x 确定,则a 的值是唯一的
B. 若a 确定,则x 的值是唯一的
C. a 是x 的平方
D. x 是a 的平方根
B
典题精讲
3
4的平方根是( )
A.16 B.2
C.±2 D.±
C
探索新知
议一议
(1)一个正数有几个平方根?
(2)0有几个平方根?
(3)负数呢?
2
知识点
平方根的性质
探索新知
平方根的性质
(1)平方根的性质:
一个正数有两个平方根;0只有一个平方
根,它是0本身;负数没有平方根.
(2)平方根的表示方法:
正数a有两个平方根,一个是a 的算术平
方根 ,另一个是 ,它们互为相反
数.这两个平方根合起来可以记作
读作“正、负根号a”.
探索新知
求下列各式的值:
(1) ; (2) ; (3) .
例2
解:
(1)因为62=36,所以 =6;
(2)因为0.92=0.81,所以 ;
(3)因为 ,所以 .
典题精讲
总 结
求一个式子的值,先分析式子的意义,特别是看清它表示的是算术平方根还是平方根,就是看清符号,最后的结果不改变它的正负性.
典题精讲
1
判断下列说法是否正确:
(1) 0的平方根是0;
(2) 1的平方根是1;
(3) -1的平方根是-1;
(4) 0.01是0.1的一个平方根.
解:
(1)正确;(2)错误;(3)错误;(4)错误.
典题精讲
2
下列说法正确的是( )
A.任何数的平方根都有两个
B.一个正数的平方根的平方就是这个数
C.负数也有平方根
D.非负数的平方根都有两个
B
典题精讲
3
下列说法正确的有( )
①-2是-4的一个平方根;
②a2的平方根是a;
③2是4的一个平方根;
④4的平方根是-2.
A.1个 B.2个
C.3个 D.4个
A
典题精讲
4
下列关于“0”的说法中,正确的是( )
A.0是最小的正整数
B.0没有相反数
C.0没有倒数
D.0没有平方根
C
探索新知
3
知识点
求平方根(开平方)
1.开平方:
求一个数a 的平方根的运算,叫做开平方, a 叫做被开方数.
2.要点精析:
(1)一个正数的正的平方根就是它的算术平方根.
(2)平方与开平方是互逆运算.开平方与加、减、乘、除、乘方
一样是一种运算,即:
运算名称:加、减、乘、除、乘方、开平方(非负数).
运算结果:和、差、积、商、幂、平方根(互为相反数).
探索新知
求下列各数的平方根:
(1) 100; (2) ; (3) 0.25.
例3
解:
(1)因为(±10)2=100,所以100的平方根是±10;
(2)因为 ,所以 的平方根是
(3)因为(±0.5)2=0.25,所以0.25的平方根是±0.5.
探索新知
总 结
要从根本之处理解一个数的平方根的运算,从平
方根的概念入手,同时要知道,只有非负数才有平方
根.同时注意平方根的通用符号是 (a≥0),防止粗
心大意漏掉“ ”而出错.
典题精讲
x 8 -8
x2 16 0.36 1
填表:
64
4
-4
0.6
-0.6
典题精讲
2
计算下列各式的值:
(1) ; (2) ; (3) .
解:
(3)因为 ,所以 .
典题精讲
3
的平方根是( )
A.± B.
C.± D.
C
4
│1+ │+│1- │ =( )
A.1 B.
C.2 D.2
D
探索新知
4
知识点
与 的性质
1.想一想:
(1) 等于多少? 等于多少?
(2) 等于多少?
(3)对于正数a, 等于多少?
2.联系拓广:
对于任意数a, 一定等于a 吗?
探索新知
1. 的化简:
2. 的化简:
典题精讲
下列结论正确的是( )
A.- =-6 B .(- )2=9
C. =±16 D.
1
A
典题精讲
下列四个数中,是负数的是( )
A. |-2| B.(-2)2
C. D.
2
C
易错提醒
下列说法不正确的是( )
A.21的平方根是±
B. 是21的一个平方根
C. 是21的算术平方根
D.21的平方根是
D
易错点:混淆平方根与算术平方根的概念而出错.
学以致用
小试牛刀
“± ”的意义是( )
A.a 的平方根
B.a 的算术平方根
C.当a≥0时,± 是a 的平方根
D.以上均不正确
C
1
小试牛刀
下列说法正确的是( )
A.|-2|=-2
B.0的倒数是0
C.4的平方根是2
D.-3的相反数是3
D
2
小试牛刀
若2m-4与3m-1是同一个数的平方根,则m的值是( )
A.-3 B.-1
C.1 D.-3或1
3
D
小试牛刀
实数a,b在数轴上对应的点的位置如图所示,化简|a|+ 的结果是( )
A.-2a+b B.2a-b
C.-b D.b
A
4
小试牛刀
求下列各数的平方根和算术平方根:
(1)225; (2) ; (3) ;(4)0.003
(1)因为(±15)2=225,所以225的平方根是±15.
因为152=225,所以225的算术平方根是15.
(2) .因为 ,
所以 的平方根是± .
因为 ,所以 的算术平方根是 .
解:
5
(3)因为 ,
所以 的平方根是±1 .
因为 ,
所以 的算术平方根是1 .
(4)因为(±0.06)2=0.003 6,所以0.003 6的平方根是±0.06.
因为0.062=0.003 6,所以0.003 6的算术平方根是0.06.
小试牛刀
小试牛刀
由(2x+1)2-121=0,得(2x+1)2=121,
所以2x+1=±11.即2x+1=11或2x+1=-11,
解得x=5或x=-6.
已知(2x+1)2-121=0,求x 的值.
解:
6
小试牛刀
解:
已知一个正数的两个平方根分别是2m+1和5-3m,求m 的值和这个正数.
因为一个正数的两个平方根互为相反数,
所以(2m+1)+(5-3m)=0,解得m=6.
此时2m+1=2×6+1=13,
5-3m=5-3×6=-13.
因为(±13)2=169,所以这个正数是169.
7
小试牛刀
已知2m+3和4m+9是一个正数的平方根,求m 的值
和这个正数的平方根.
分两种情况进行讨论:
(1)当2m+3≠4m+9时,得(2m+3)+(4m+9)=0,
解得m=-2.所以2m+3=2×(-2)+3=-1,
4m+9=4×(-2)+9=1.
所以这个正数的平方根是±1.
(2)当2m+3=4m+9时,得m=-3,
此时这个正数为(2m+3)2=9.
所以这个正数的平方根为±3.
解:
8
小试牛刀
已知2m+2的平方根是±4,3m+n+1的平方根是
±5,求m+2n的值.
由题意,得2m+2=(±4)2=16,
3m+n+1=(±5)2=25,解得m=7,n=3.
所以m+2n=7+2×3=13.
解:
9
小试牛刀
阅读下列材料:
当a>0时,如a=6,则|a|=|6|=6,故此时a 的绝对值是它本身;
当a=0时,|a|=|0|=0,故此时a 的绝对值是0;
当a<0时,如a=-6,则|a|=|-6|=-(-6),故此时a 的绝
对值是它的相反数.
综上可知,
|a|=
这种分析方法渗透了数学中的分类讨论思想.
10
小试牛刀
回答下列问题:
(1)请仿照材料中的分类讨论思想,分析 的情况;
(2)猜想 与|a|的大小关系.
(1)当a>0时,如a=5,则 =5,故此时 =a;
当a=0时, =0;当a<0时,如a=-5,
则 =-(-5),故此时 =-a.
综上可知, =
(2) =|a|.
解:
11
小试牛刀
已知a,b,c 在数轴上对应点的位置如图所示,
化简 .
解:
由a,b,c在数轴上对应点的位置可知a<0,
a+b<0,c-a>0,b+c<0,
所以原式=|a|-|a+b|+(c-a)+|b+c|
=-a+(a+b)+c-a-(b+c)
=-a+a+b+c-a-b-c
=-a.
12
课堂小结
课堂小结
1. 定义:若x2=a,则x 叫做a 的平方根.
2. 性质:一个正数有两个平方根,它们互为相反数,
0的平方根是0,负数没有平方根.
3. 平方根与开平方间的关系:
(1)开平方是求平方根的运算;
(2)平方根是开平方运算的结果.
课堂小结
求一个非负数的平方根的方法:
① 求一个非负数a 的平方根,就是要把平方后等于a 的
数找出来,从而求出a 的所有平方根;
② 求带分数的平方根时,应先将带分数化为假分数,
这也是常出错的地方.
注意:正数的平方根有两个,前面必定有“±”号.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
