【班海精品】人教版(新)七下-6.1 平方根 第一课时【优质课件】
文档属性
| 名称 | 【班海精品】人教版(新)七下-6.1 平方根 第一课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 11.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 10:20:43 | ||
图片预览









文档简介
(共45张PPT)
6.1 平 方 根
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
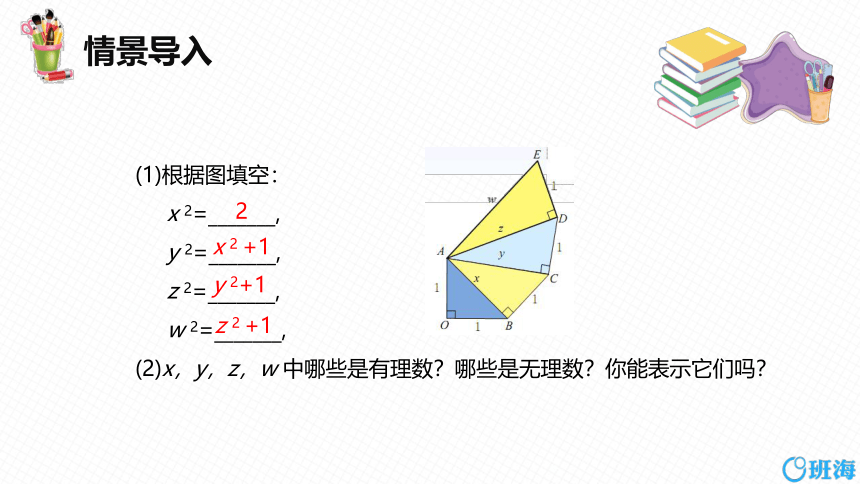
(1)根据图填空:
x 2=_______,
y 2=_______,
z 2=_______,
w 2=_______,
(2)x,y,z,w 中哪些是有理数?哪些是无理数?你能表示它们吗?
2
x 2 +1
y 2+1
z 2 +1
新课精讲
探索新知
1
知识点
算术平方根的定义
问题1:正数3的平方等于9,若x 2=9,则正数x=____.
正数4的平方等于16,若x 2=16,则正数x=____.
说说6和36这两个数又怎样的关系呢?
问题2:(1) 0的平方是___,如果x 2=0,那么x=____.
(2) 0的算术平方根是___.
探索新知
问题3:学校要举行美术作品比赛,小鸥想裁出一块面积为25 dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少
你一定会算出边长应取5 dm. 说
一说,你是怎样算出来的?
因为52=25,所以这个正方形画
布的边长应取5 dm.
探索新知
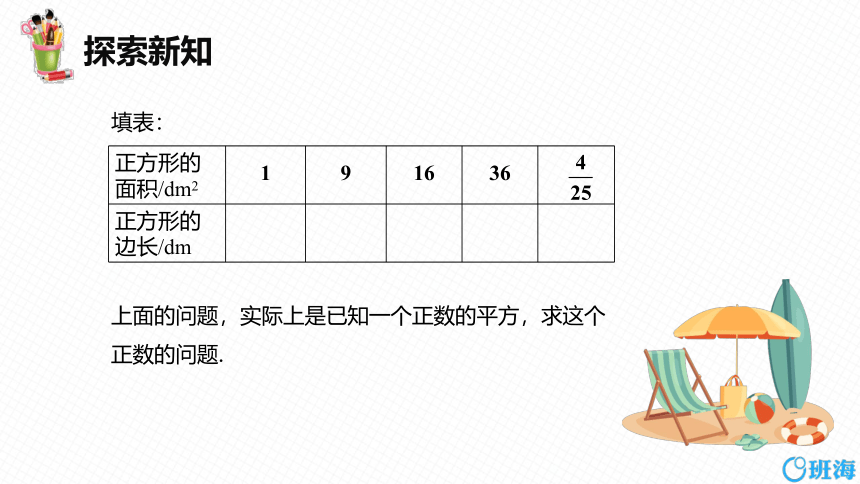
填表:
上面的问题,实际上是已知一个正数的平方,求这个
正数的问题.
正方形的面积/dm2 1 9 16 36
正方形的边长/dm
探索新知
定义:一般地,如果一个正数x 的平方等于a, 即x 2=a,那么这个正数x 就叫做a 的算术平方根.
规定:0的算术平方根是0.
表示方法:正数a 的算术平方根表示为 读作 “根号a”.
探索新知
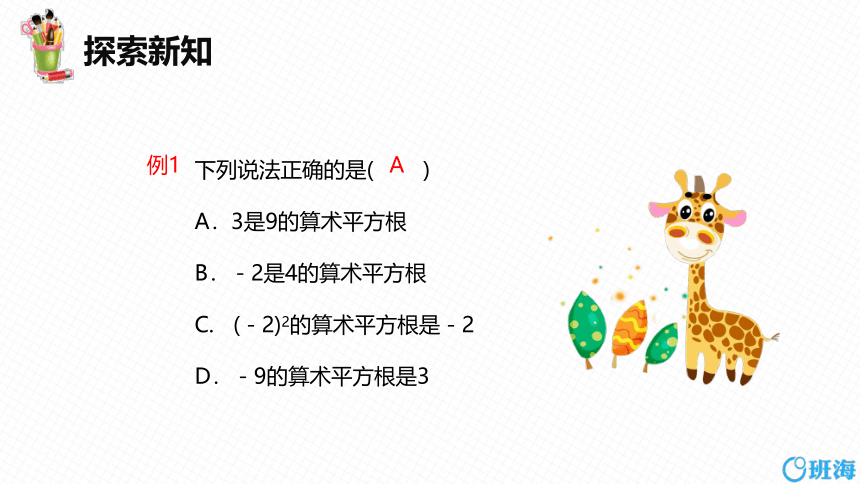
下列说法正确的是( )
A.3是9的算术平方根
B.-2是4的算术平方根
C. (-2)2的算术平方根是-2
D.-9的算术平方根是3
例1
A
探索新知
导引:
要正确把握算术平方根的定义.因为3的平方等于9,所以3是9的算术平方根;因为-2不是正数,所以-2不是4的算术平方根;因为(-2)2 =4,而22=4,所以2是(-2)2的算术平方根;
负数没有算术平方根.
探索新知
总 结
算术平方根具有双重非负性:这个数是非负数,它的算术平方根也是非负数.
典题精讲
1 9的算术平方根为( )
A. 3 B.-3 C.±3 D.
2 下列说法正确的是( )
A.因为62=36,所以6是36的算术平方根
B.因为(-6)2=36,所以-6是36的算术平方根
C.因为(±6)2=36,所以6和-6都是36的算术平方根
D.以上说法都不对
A
A
典题精讲
3
下列说法正确的是( )
A. 表示25的算术平方根
B.- 表示2的算术平方根
C.2的算术平方根记作±
D.2是 的算术平方根
A
探索新知
(1) 正数的算术平方根是一个正数;
(2) 0的算术平方根是0;
(3) 负数没有算术平方根;
(4) 被开方数越大,对应的算术平方根也越大.
2
知识点
求算术平方根
探索新知
求下列各数的算术平方根:
(1) 100; (2) ; (3) 0.0001.
例2
解:
(1)因为102 = 100,所以100的算术平方根是10,
即
(2)因为( )2 = ,所以 的算术平方根是 ,
即 ;
(3)因为0.012 =0.0001,所以0.0001的算术平方
根是0.01,即 =0.01.
探索新知
总 结
(1)求一个数的算术平方根时,首先要弄清是求哪个数
的算术平方根,分清求 与81的算术平方根的不
同意义,不要被表面现象迷惑.
(2)求一个非负数的算术平方根常借助于平方运算,因
此熟记常用平方数对求一个数的算术平方根十分有用.
典题精讲
1
求下列各数的算术平方根:
(1) 0.0025; (2) 81; (3) 32.
解:
(1)因为0.052=0.002 5,所以0.002 5的算术平方
根是0.05,即 =0.05;
(2)因为92=81,所以81的算术平方根是9,
即 =9;
(3)因为32=9,9的算术平方根是3,所以32的算
术平方根是3,即 =3.
典题精讲
2
求下列各式的值:
(1) ; (2) ; (3) .
解:
典题精讲
3
计算 的结果为( )
A.6 B.-6
C.18 D.-18
设 =a,则下列结论正确的是( )
A.a=441 B.a=4412
C.a=-21 D.a=21
4
A
D
典题精讲
5
下列说法:
①-4的算术平方根是-2;
②3的算术平方根是9;
③ 是7的算术平方根;
④64的算术平方根是8.其中错误的有( )
A.1个 B.2个
C.3个 D.4个
B
典题精讲
6
一个自然数的算术平方根为a,则和这个自然数相邻的下一个自然数是( )
A.a+1 B.a2+1
C. D.
B
探索新知
3
知识点
算术平方根的双重非负性
问题1: (1)因为_____2=64,所以64的算术平方根是______,即 =______.
(2)因为_____2=0.25,所以0.25的算术平方根是______,即 =______.
(3)因为_____2=0,所以0的算术平方根是______,即 =______.
8
8
8
0.5
0.5
0.5
0
0
问题2: 讨论:在 中,被开方数a是一个______数,
算术平方根 是一个______数.
非负
非负
0
探索新知
归 纳
所以算术平方根 具有双重非负性:
1. 被开方数a 是非负数,即a ≥0;
2. 算术平方根 本身是非负数,即
探索新知
若 =0,求x 2 015+y 2 016的值.
例3
导引:
非负数与非负数的和为0当且仅当这两个非负数
为0时成立,可列方程求出x,y 的值,从而求出
代数式的值.
∵ ≥0, ≥0, =0,
∴x-1=0,y+1=0,∴x=1,y=-1.
∴x 2 015+y 2 016=12 015+(-1)2 016=2.
解:
探索新知
总 结
算术平方根和绝对值一样,都是非负数,当几个非负数的和等于0时,其中每一个非负数都为0.
典题精讲
(1) 中,被开方数a是 ,即a_______0;
(2) 是________,即 ________0,即非负数的
算术平方根是_______;负数没有算术平方根,
即当a________0时, 无意义.
1
非负数
≥
非负数
≥
非负数
<
典题精讲
2
要使 有意义,则x 的取值范围是( )
A.x<1 B.x≥1
C.x≤-1 D.x<-1
B
3
若 +b2-4b+4=0,则ab 的值等于( )
A.-2 B.0
C.1 D.2
D
典题精讲
4
下列说法中不正确的有( )
①一个数的算术平方根一定是正数;
②100的算术平方根是10,记作 =10;
③(π-3.14)2的算术平方根是π-3.14;
④a2的算术平方根为a.
A.1个 B.2个
C.3个 D.4个
B
易错提醒
求 的算术平方根.
解:
因为 =9, =3, 所以的算术平方根是3.
易错点:误将求 的算术平方根求成a 的算术平方根造成错误.
学以致用
小试牛刀
如图,每个小正方形的边长为1,把阴影部分剪下来,再用剪下来的阴影部分拼成一个正方形,那么新正方形的边长是( )
A.
B.2
C.
D.
C
1
小试牛刀
若 + +1有意义,则x 满足的条件是( )
A.x≥ B.x≤
C.x= D.x≠
C
2
小试牛刀
求下列各数的算术平方根:
(1)0.04;(2)0.64;(3)(-3)2;(4) .
(1)因为0.22=0.04,所以0.04的算术平方根是0.2,
即 =0.2.
(2)因为0.82=0.64,所以0.64的算术平方根是0.8,
即 =0.8.
解:
3
小试牛刀
(3)因为32=(-3)2,所以(-3)2的算术平方根是3,
即 =3.
.因为 ,
所以 的算术平方根是 ,
即 .
小试牛刀
由题意知a= =3, b=±4.当b=4时,a-b=3-4=-1;当b=-4时,a-b=3-(-4)=7.
已知9的算术平方根为a,b 的绝对值为4,求a-b 的值.
解:
4
小试牛刀
解:
已知2a+1的算术平方根是0,b-a 的算术平方根是 ,求 ab 的算术平方根.
因为 =0,所以2a+1=0,解得a=- .
因为 ,所以 ,所以b-a= ,
所以b=- , 所以 ab= .
又因为 ,所以 ,
所以 .
5
小试牛刀
若|x-1|+(y+3)2+ =0,求x+y+z
的算术平方根.
由题意知x-1=0,y+3=0,x-y-2z=0,解得x=1,y=-3,z=2,∴ =0.
解:
已知x,y 都是有理数,且 y= +3,
求2x-y 的值.
由题意得2-x=0,解得x=2,所以y=3.
因此2x-y=2×2-3=1.
解:
6
7
小试牛刀
(1)通过计算下列各式的值探究问题.
① = ; = ;
= ; = .
探究:对于任意非负有理数a, = .
② = ; = ;
= ; = .
探究:对于任意负有理数a, = .
综上,对于任意有理数a, = .
4
16
a
0
3
5
1
2
-a
|a|
8
小试牛刀
(2)应用(1)所得结论解决问题:有理数a,b在数轴上对应的
点的位置如图所示,化简 +|a+b|.
(2)由数轴可知a<0,b>0,a-b<0,a+b<0,
所以|a|=-a,|b|=b,|a-b|=-(a-b),|a+b|=
-(a+b).所以原式=|a|-|b|-|a-b|+|a+b|=
-a-b+(a-b)-(a+b)=-a-b+a-b-a-b
=-a-3b.
解:
小试牛刀
观察: ,
(1) 等于什么?
(2)写出第八个等式.
(3)写出符合这一规律的一般等式(用字母n 表示,n 为自然数,且n≥2).
9
小试牛刀
解:
(3) =n (n为自然数,且n≥2).
课堂小结
课堂小结
1. 表示的是a的算术平方根,由算术平方
根的定义知它具有“双重”非负性:a≥0,
≥0,即算术平方根及它的被开方数都
为非负数.
2.对于所有的算术平方根,被开方数越大,对
应的算术平方根也越大;反之亦然.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
6.1 平 方 根
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
(1)根据图填空:
x 2=_______,
y 2=_______,
z 2=_______,
w 2=_______,
(2)x,y,z,w 中哪些是有理数?哪些是无理数?你能表示它们吗?
2
x 2 +1
y 2+1
z 2 +1
新课精讲
探索新知
1
知识点
算术平方根的定义
问题1:正数3的平方等于9,若x 2=9,则正数x=____.
正数4的平方等于16,若x 2=16,则正数x=____.
说说6和36这两个数又怎样的关系呢?
问题2:(1) 0的平方是___,如果x 2=0,那么x=____.
(2) 0的算术平方根是___.
探索新知
问题3:学校要举行美术作品比赛,小鸥想裁出一块面积为25 dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少
你一定会算出边长应取5 dm. 说
一说,你是怎样算出来的?
因为52=25,所以这个正方形画
布的边长应取5 dm.
探索新知
填表:
上面的问题,实际上是已知一个正数的平方,求这个
正数的问题.
正方形的面积/dm2 1 9 16 36
正方形的边长/dm
探索新知
定义:一般地,如果一个正数x 的平方等于a, 即x 2=a,那么这个正数x 就叫做a 的算术平方根.
规定:0的算术平方根是0.
表示方法:正数a 的算术平方根表示为 读作 “根号a”.
探索新知
下列说法正确的是( )
A.3是9的算术平方根
B.-2是4的算术平方根
C. (-2)2的算术平方根是-2
D.-9的算术平方根是3
例1
A
探索新知
导引:
要正确把握算术平方根的定义.因为3的平方等于9,所以3是9的算术平方根;因为-2不是正数,所以-2不是4的算术平方根;因为(-2)2 =4,而22=4,所以2是(-2)2的算术平方根;
负数没有算术平方根.
探索新知
总 结
算术平方根具有双重非负性:这个数是非负数,它的算术平方根也是非负数.
典题精讲
1 9的算术平方根为( )
A. 3 B.-3 C.±3 D.
2 下列说法正确的是( )
A.因为62=36,所以6是36的算术平方根
B.因为(-6)2=36,所以-6是36的算术平方根
C.因为(±6)2=36,所以6和-6都是36的算术平方根
D.以上说法都不对
A
A
典题精讲
3
下列说法正确的是( )
A. 表示25的算术平方根
B.- 表示2的算术平方根
C.2的算术平方根记作±
D.2是 的算术平方根
A
探索新知
(1) 正数的算术平方根是一个正数;
(2) 0的算术平方根是0;
(3) 负数没有算术平方根;
(4) 被开方数越大,对应的算术平方根也越大.
2
知识点
求算术平方根
探索新知
求下列各数的算术平方根:
(1) 100; (2) ; (3) 0.0001.
例2
解:
(1)因为102 = 100,所以100的算术平方根是10,
即
(2)因为( )2 = ,所以 的算术平方根是 ,
即 ;
(3)因为0.012 =0.0001,所以0.0001的算术平方
根是0.01,即 =0.01.
探索新知
总 结
(1)求一个数的算术平方根时,首先要弄清是求哪个数
的算术平方根,分清求 与81的算术平方根的不
同意义,不要被表面现象迷惑.
(2)求一个非负数的算术平方根常借助于平方运算,因
此熟记常用平方数对求一个数的算术平方根十分有用.
典题精讲
1
求下列各数的算术平方根:
(1) 0.0025; (2) 81; (3) 32.
解:
(1)因为0.052=0.002 5,所以0.002 5的算术平方
根是0.05,即 =0.05;
(2)因为92=81,所以81的算术平方根是9,
即 =9;
(3)因为32=9,9的算术平方根是3,所以32的算
术平方根是3,即 =3.
典题精讲
2
求下列各式的值:
(1) ; (2) ; (3) .
解:
典题精讲
3
计算 的结果为( )
A.6 B.-6
C.18 D.-18
设 =a,则下列结论正确的是( )
A.a=441 B.a=4412
C.a=-21 D.a=21
4
A
D
典题精讲
5
下列说法:
①-4的算术平方根是-2;
②3的算术平方根是9;
③ 是7的算术平方根;
④64的算术平方根是8.其中错误的有( )
A.1个 B.2个
C.3个 D.4个
B
典题精讲
6
一个自然数的算术平方根为a,则和这个自然数相邻的下一个自然数是( )
A.a+1 B.a2+1
C. D.
B
探索新知
3
知识点
算术平方根的双重非负性
问题1: (1)因为_____2=64,所以64的算术平方根是______,即 =______.
(2)因为_____2=0.25,所以0.25的算术平方根是______,即 =______.
(3)因为_____2=0,所以0的算术平方根是______,即 =______.
8
8
8
0.5
0.5
0.5
0
0
问题2: 讨论:在 中,被开方数a是一个______数,
算术平方根 是一个______数.
非负
非负
0
探索新知
归 纳
所以算术平方根 具有双重非负性:
1. 被开方数a 是非负数,即a ≥0;
2. 算术平方根 本身是非负数,即
探索新知
若 =0,求x 2 015+y 2 016的值.
例3
导引:
非负数与非负数的和为0当且仅当这两个非负数
为0时成立,可列方程求出x,y 的值,从而求出
代数式的值.
∵ ≥0, ≥0, =0,
∴x-1=0,y+1=0,∴x=1,y=-1.
∴x 2 015+y 2 016=12 015+(-1)2 016=2.
解:
探索新知
总 结
算术平方根和绝对值一样,都是非负数,当几个非负数的和等于0时,其中每一个非负数都为0.
典题精讲
(1) 中,被开方数a是 ,即a_______0;
(2) 是________,即 ________0,即非负数的
算术平方根是_______;负数没有算术平方根,
即当a________0时, 无意义.
1
非负数
≥
非负数
≥
非负数
<
典题精讲
2
要使 有意义,则x 的取值范围是( )
A.x<1 B.x≥1
C.x≤-1 D.x<-1
B
3
若 +b2-4b+4=0,则ab 的值等于( )
A.-2 B.0
C.1 D.2
D
典题精讲
4
下列说法中不正确的有( )
①一个数的算术平方根一定是正数;
②100的算术平方根是10,记作 =10;
③(π-3.14)2的算术平方根是π-3.14;
④a2的算术平方根为a.
A.1个 B.2个
C.3个 D.4个
B
易错提醒
求 的算术平方根.
解:
因为 =9, =3, 所以的算术平方根是3.
易错点:误将求 的算术平方根求成a 的算术平方根造成错误.
学以致用
小试牛刀
如图,每个小正方形的边长为1,把阴影部分剪下来,再用剪下来的阴影部分拼成一个正方形,那么新正方形的边长是( )
A.
B.2
C.
D.
C
1
小试牛刀
若 + +1有意义,则x 满足的条件是( )
A.x≥ B.x≤
C.x= D.x≠
C
2
小试牛刀
求下列各数的算术平方根:
(1)0.04;(2)0.64;(3)(-3)2;(4) .
(1)因为0.22=0.04,所以0.04的算术平方根是0.2,
即 =0.2.
(2)因为0.82=0.64,所以0.64的算术平方根是0.8,
即 =0.8.
解:
3
小试牛刀
(3)因为32=(-3)2,所以(-3)2的算术平方根是3,
即 =3.
.因为 ,
所以 的算术平方根是 ,
即 .
小试牛刀
由题意知a= =3, b=±4.当b=4时,a-b=3-4=-1;当b=-4时,a-b=3-(-4)=7.
已知9的算术平方根为a,b 的绝对值为4,求a-b 的值.
解:
4
小试牛刀
解:
已知2a+1的算术平方根是0,b-a 的算术平方根是 ,求 ab 的算术平方根.
因为 =0,所以2a+1=0,解得a=- .
因为 ,所以 ,所以b-a= ,
所以b=- , 所以 ab= .
又因为 ,所以 ,
所以 .
5
小试牛刀
若|x-1|+(y+3)2+ =0,求x+y+z
的算术平方根.
由题意知x-1=0,y+3=0,x-y-2z=0,解得x=1,y=-3,z=2,∴ =0.
解:
已知x,y 都是有理数,且 y= +3,
求2x-y 的值.
由题意得2-x=0,解得x=2,所以y=3.
因此2x-y=2×2-3=1.
解:
6
7
小试牛刀
(1)通过计算下列各式的值探究问题.
① = ; = ;
= ; = .
探究:对于任意非负有理数a, = .
② = ; = ;
= ; = .
探究:对于任意负有理数a, = .
综上,对于任意有理数a, = .
4
16
a
0
3
5
1
2
-a
|a|
8
小试牛刀
(2)应用(1)所得结论解决问题:有理数a,b在数轴上对应的
点的位置如图所示,化简 +|a+b|.
(2)由数轴可知a<0,b>0,a-b<0,a+b<0,
所以|a|=-a,|b|=b,|a-b|=-(a-b),|a+b|=
-(a+b).所以原式=|a|-|b|-|a-b|+|a+b|=
-a-b+(a-b)-(a+b)=-a-b+a-b-a-b
=-a-3b.
解:
小试牛刀
观察: ,
(1) 等于什么?
(2)写出第八个等式.
(3)写出符合这一规律的一般等式(用字母n 表示,n 为自然数,且n≥2).
9
小试牛刀
解:
(3) =n (n为自然数,且n≥2).
课堂小结
课堂小结
1. 表示的是a的算术平方根,由算术平方
根的定义知它具有“双重”非负性:a≥0,
≥0,即算术平方根及它的被开方数都
为非负数.
2.对于所有的算术平方根,被开方数越大,对
应的算术平方根也越大;反之亦然.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
