归纳推理课件[上学期]
图片预览








文档简介
课件25张PPT。归 纳 推 理 前提 当n=0时,n2-n+11=11
当n=1时,n2-n+11=11
当n=2时,n2-n+11=13
当n=3时,n2-n+11=17
当n=4时,n2-n+11=23
当n=5时,n2-n+11=31 结论 对于所有的自然数n,
n2-n+11的值都是质数11,11,13,17,23,31都是质数 “任何一个大于2的偶数都可以表示为两个素数之和”----歌德巴赫猜想结论:哥德巴赫猜想
(Goldbach Conjecture)
目前最佳的结果是中国数学家陈景润於1966年证明的,称为陈氏定理 .“任何充份大的偶数都是一个质数与一个自然数之和,而後者仅仅是两个质数的乘积。” 通常都简称这个结果为大偶数可表示为 “1 + 2 ”的形式。从个别事实中推演出一般性的结论,称为归纳推理.归纳推理的几个特点:1.归纳是依据特殊现象推断一般现象,因而,由归纳所得的结论超越了前提所包容的范围.2.归纳是依据若干已知的、没有穷尽的现象推断尚属未知的现象,因而结论具有猜测性.3.归纳的前提是特殊的情况,因而归纳是立足于观察、经验和实验的基础之上. 归纳是立足于观察、经验、实验和对有限资料分析的基础上.提出带有规律性的结论.需证明归纳推理的一般步骤:试验、观察概括、推广猜测一般性结论 例1.已知数列{an}的第1项a1=1,且
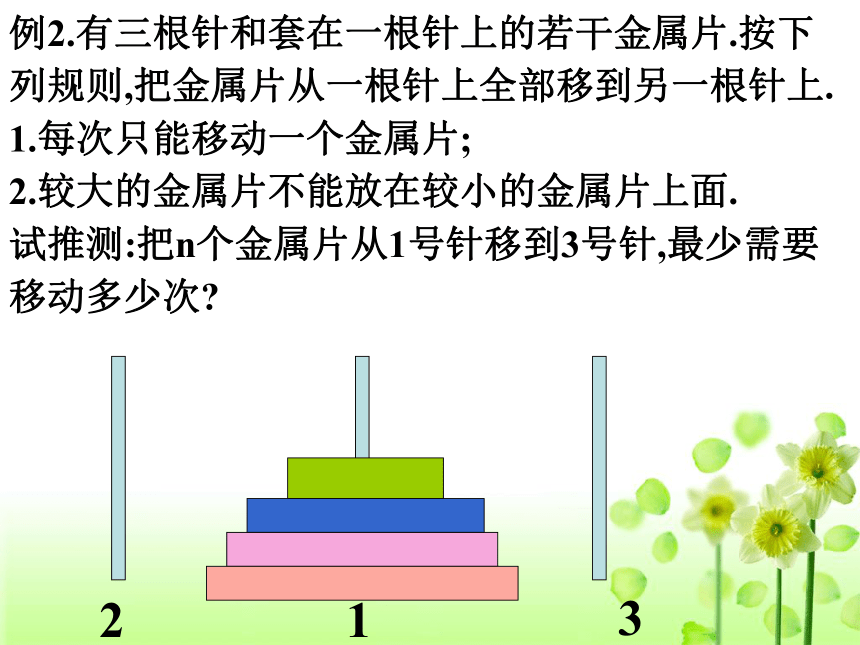
(n=1 , 2 , …),试归纳出这个数列的通项公式.分别把n=1,2,3,4代入 得:归纳:可用数学归纳法证明这个猜想是正确的.取倒数得:解法2、构造法例2.有三根针和套在一根针上的若干金属片.按下列规则,把金属片从一根针上全部移到另一根针上.
1.每次只能移动一个金属片;
2.较大的金属片不能放在较小的金属片上面.
试推测:把n个金属片从1号针移到3号针,最少需要移动多少次?n=1时,n=2时,n=1时,n=3时,n=2时,n=1时,n=2时,n=1时,n=3时,n=4时,n=3时,n=2时,n=1时,n=4时,n=3时,n=2时,n=1时,归纳:例3(2004春季上海)根据图中5个图形及相应点的个数的变化规律,试猜测第n个图形中有 个点.(1)(2)(3)(4)(5)例4(2005年广东)设平面内有n条直线(n≥3),其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用f(n)表示这n条直线交点的个数,f(4)= ,
当n>4时,f(n)= .(用n表示)累加得:例2:数一数图中的凸多面体的面数F、顶点数V和棱数E,然后用归纳法推理得出它们之间的关系.46455659846455659866861281261046455659866861281261077916910151015F+V-E=2猜想欧拉公式(2001年上海)已知两个圆①x2+y2=1:与②x2+(y-3)2=1,则由①式减去②式可得上述两圆的对称轴方程.将上述命题在曲线仍然为圆的情况下加以推广,即要求得到一个更一般的命题,而已知命题应成为所推广命题的一个特例,推广的命题为:设圆的方程为①(x-a)2+(y-b)2=r2与
②(x-c)2+(y-d)2=r2(a≠c或b≠d),
则由①式减去②式可得上述两圆的对称轴
方程.小结2.归纳推理的一般步骤:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).1.什么是归纳推理(简称归纳)?部分 整体个别 一般作 业 1.已知数列{an}的前n项和Sn , 且
计算S1 , S2 , S3 , S4 ,并猜想Sn的表达式.猜想:计算得:
当n=1时,n2-n+11=11
当n=2时,n2-n+11=13
当n=3时,n2-n+11=17
当n=4时,n2-n+11=23
当n=5时,n2-n+11=31 结论 对于所有的自然数n,
n2-n+11的值都是质数11,11,13,17,23,31都是质数 “任何一个大于2的偶数都可以表示为两个素数之和”----歌德巴赫猜想结论:哥德巴赫猜想
(Goldbach Conjecture)
目前最佳的结果是中国数学家陈景润於1966年证明的,称为陈氏定理 .“任何充份大的偶数都是一个质数与一个自然数之和,而後者仅仅是两个质数的乘积。” 通常都简称这个结果为大偶数可表示为 “1 + 2 ”的形式。从个别事实中推演出一般性的结论,称为归纳推理.归纳推理的几个特点:1.归纳是依据特殊现象推断一般现象,因而,由归纳所得的结论超越了前提所包容的范围.2.归纳是依据若干已知的、没有穷尽的现象推断尚属未知的现象,因而结论具有猜测性.3.归纳的前提是特殊的情况,因而归纳是立足于观察、经验和实验的基础之上. 归纳是立足于观察、经验、实验和对有限资料分析的基础上.提出带有规律性的结论.需证明归纳推理的一般步骤:试验、观察概括、推广猜测一般性结论 例1.已知数列{an}的第1项a1=1,且
(n=1 , 2 , …),试归纳出这个数列的通项公式.分别把n=1,2,3,4代入 得:归纳:可用数学归纳法证明这个猜想是正确的.取倒数得:解法2、构造法例2.有三根针和套在一根针上的若干金属片.按下列规则,把金属片从一根针上全部移到另一根针上.
1.每次只能移动一个金属片;
2.较大的金属片不能放在较小的金属片上面.
试推测:把n个金属片从1号针移到3号针,最少需要移动多少次?n=1时,n=2时,n=1时,n=3时,n=2时,n=1时,n=2时,n=1时,n=3时,n=4时,n=3时,n=2时,n=1时,n=4时,n=3时,n=2时,n=1时,归纳:例3(2004春季上海)根据图中5个图形及相应点的个数的变化规律,试猜测第n个图形中有 个点.(1)(2)(3)(4)(5)例4(2005年广东)设平面内有n条直线(n≥3),其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用f(n)表示这n条直线交点的个数,f(4)= ,
当n>4时,f(n)= .(用n表示)累加得:例2:数一数图中的凸多面体的面数F、顶点数V和棱数E,然后用归纳法推理得出它们之间的关系.46455659846455659866861281261046455659866861281261077916910151015F+V-E=2猜想欧拉公式(2001年上海)已知两个圆①x2+y2=1:与②x2+(y-3)2=1,则由①式减去②式可得上述两圆的对称轴方程.将上述命题在曲线仍然为圆的情况下加以推广,即要求得到一个更一般的命题,而已知命题应成为所推广命题的一个特例,推广的命题为:设圆的方程为①(x-a)2+(y-b)2=r2与
②(x-c)2+(y-d)2=r2(a≠c或b≠d),
则由①式减去②式可得上述两圆的对称轴
方程.小结2.归纳推理的一般步骤:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).1.什么是归纳推理(简称归纳)?部分 整体个别 一般作 业 1.已知数列{an}的前n项和Sn , 且
计算S1 , S2 , S3 , S4 ,并猜想Sn的表达式.猜想:计算得:
