分类计数原理和分步计数原理(一)[下学期]
文档属性
| 名称 | 分类计数原理和分步计数原理(一)[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 44.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-06-30 23:24:00 | ||
图片预览




文档简介
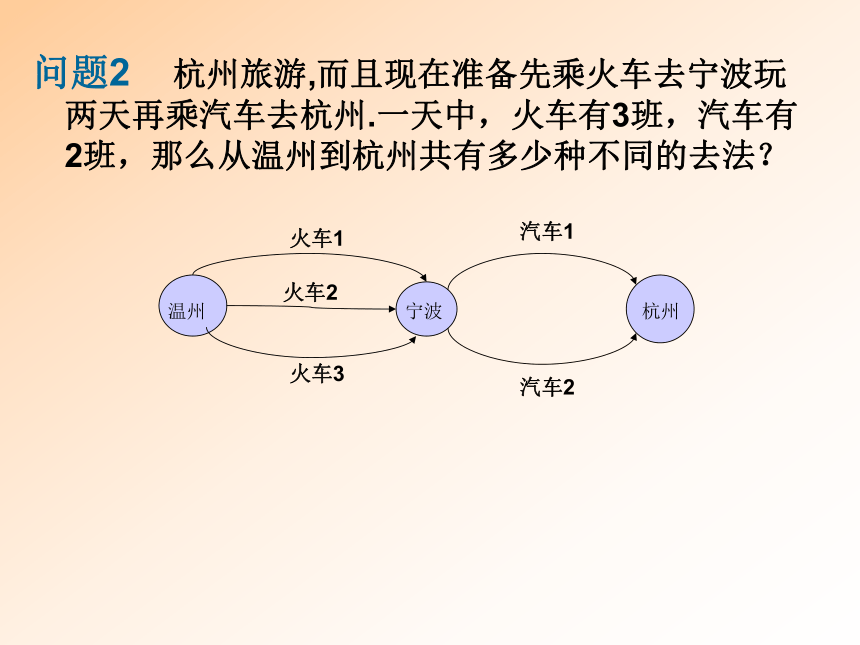
课件11张PPT。问题1. 从温州到杭州旅游,可以乘火车,也可以乘汽车。一天中,火车有3班,汽车有2班。那么一天当中,乘坐这些交通工具从温州到杭州共有多少种不同的去法?火车1火车2火车3汽车2汽车1温州杭州分类计数原理分类计数原理: 完成一件事,有n类办法,在第1类办法中有m1种不同的方法,在第2类办法中m2种不同的方法……在第n类办法中有mn种不同的方法。那么完成这件事共有
N=m1十m2十……十mn
种不同的方法。问题2 杭州旅游,而且现在准备先乘火车去宁波玩两天再乘汽车去杭州.一天中,火车有3班,汽车有2班,那么从温州到杭州共有多少种不同的去法?火车1火车2火车3汽车1汽车2温州宁波杭州分步计数原理分步计数原理: 完成一件事,需要分成n个步骤,做第一个步骤有m1种不同的方法,做第二个步骤有m2种不同的方法……做第n个步骤有mn种不同的方法,那么完成这件事共有 N=m1·m2……mn
种不同的方法。 例1 李平同学有若干本各不相同学习参考书,其中数学4本,语文3本,英语5本。
⑴若从这些书中带一本去图书馆,共有多少种不同的带法?
⑵若各科书各带一本,共有多少种不同的带法?解:⑴从中带一本书,有三类办法:
第一类办法是带数学书,可以从 4本书中任选一本,有 4种选法; 第二类办法是带语文书,可以从3本书中任选一本,有3种选法。根据分类计数原理,得到不同的取法的种数是:
N = m1+ m2 + m3 = 4+3+5=12
答:从书架上任取一本书,有12种不同的取法。 第三类办法是带英语书,可以从5本书中任选一本,有5 种选法。 解: ⑵带每科书各一本,可以分成三个步骤完成:
第一步选一本数学书,有4种方法;根据分步计数原理,得到不同的取法的种数是:
N= m1× m2 × m3 = 4×3×5 = 60
答: 从书架上取数学书与语文书各一本,共有60 种不同的取法。思考:若任取三门学科中的两门呢?有多少种不同的取法?例1 李平同学有若干本各不相同学习参考书,其中数学4本,语文3本,英语5本。
⑴若从这些书中带一本去图书馆,共有多少种不同的带法?
⑵若各科书各带一本,共有多少种不同的带法?第二步选一本语文书,有3种方法;第三步选一本英语书,有5种方法。例2 有数字 1,2,3,4,5 可以组成多少个三位数(各位上的数字许重复)?解:要组成一个三位数可以分成三个步骤完成:
第一步确定百位上的数字,从5个数字中任选一个数字,共有5种选法; 第二步确定十位上的数字,由于数字允许重复,这仍有5种选法; 第三步确定十位上的数字,同理,它也有5种选法。 根据分步计数原理,得到组成的三位数的个数是:
N = 5 ×5 ×5 = 53 = 125
答:可以组成125个三位数。例3 要从甲、乙、丙3名工人中选2名分别上日班和晚班,有多少种不同的选法?解:安排出日晚班可分两个步骤完成:
第一步:从3名工人中选1人上日班,有3种选法。由分步计数原理得 3 × 2= 6答:共有 6 种选法。第二步:从剩余的2名工人中选1人上晚班,只有2种选法。两个原理区别 分类计数原理与分步计数原理,回答的都是有关做一件事的不同方法种数的问题。区别在于:分类计数原理针对的是“分类”问题,其中各种方法相互独立,用其中任何一种方法都可以做完这件事;分步计数原理针对的是“分步”问题,各个步骤中的方法相互依存,只有各个步骤都完成才算做完这件事。 1. 一件工作可以用两种方法完成。有5人会用第一种方法完成,另有4人会用第二种方法完成。选出一个人来完成这件工作,共有多少种选法?
2.乘积( a1+ a 2+ a 3 )( b1 + b 2 + b3 + b4 )(c1 + c2 + c3 + c4 + c5 )展开后共有项? 4 + 5 = 93×4×5=60练习2:1、把四封不同的信任意投入三个信箱中,不同投法种数是( )
A. 12 B.64 C.81 D.72、火车上有10名乘客,沿途有5个车站,乘客下车的可能方式有 ( )种
A. 510 B. 105 C. 50 D. 以上都不对练习1:CA总结:
1.分类计数原理:做一件事,完成它可以有 n 类办法,在第一类办法中有m1种不同的方法,在第一类办法中有m2种不同的方法,… …,在第n类办法中有mn种不同的方法。那麽完成这件事共有 N= m1+ m2+… …+ mn 种不同的方法。
分步计数原理:做一件事,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,… …,做第n步有mn种不同的方法。那麽完成这件事共有 N= m1× m2×… …×mn 种不同的方法。
2.分类计数原理和分步计数原理的
共同点:都是把一个事件分解成若干个分事件来完成;
不同点:前者分类,后者分步;如果分事件相互独立,分类完
备,就用分类计数原理;如果分事件相互关联,缺一
不可,就用分步计数原理。
N=m1十m2十……十mn
种不同的方法。问题2 杭州旅游,而且现在准备先乘火车去宁波玩两天再乘汽车去杭州.一天中,火车有3班,汽车有2班,那么从温州到杭州共有多少种不同的去法?火车1火车2火车3汽车1汽车2温州宁波杭州分步计数原理分步计数原理: 完成一件事,需要分成n个步骤,做第一个步骤有m1种不同的方法,做第二个步骤有m2种不同的方法……做第n个步骤有mn种不同的方法,那么完成这件事共有 N=m1·m2……mn
种不同的方法。 例1 李平同学有若干本各不相同学习参考书,其中数学4本,语文3本,英语5本。
⑴若从这些书中带一本去图书馆,共有多少种不同的带法?
⑵若各科书各带一本,共有多少种不同的带法?解:⑴从中带一本书,有三类办法:
第一类办法是带数学书,可以从 4本书中任选一本,有 4种选法; 第二类办法是带语文书,可以从3本书中任选一本,有3种选法。根据分类计数原理,得到不同的取法的种数是:
N = m1+ m2 + m3 = 4+3+5=12
答:从书架上任取一本书,有12种不同的取法。 第三类办法是带英语书,可以从5本书中任选一本,有5 种选法。 解: ⑵带每科书各一本,可以分成三个步骤完成:
第一步选一本数学书,有4种方法;根据分步计数原理,得到不同的取法的种数是:
N= m1× m2 × m3 = 4×3×5 = 60
答: 从书架上取数学书与语文书各一本,共有60 种不同的取法。思考:若任取三门学科中的两门呢?有多少种不同的取法?例1 李平同学有若干本各不相同学习参考书,其中数学4本,语文3本,英语5本。
⑴若从这些书中带一本去图书馆,共有多少种不同的带法?
⑵若各科书各带一本,共有多少种不同的带法?第二步选一本语文书,有3种方法;第三步选一本英语书,有5种方法。例2 有数字 1,2,3,4,5 可以组成多少个三位数(各位上的数字许重复)?解:要组成一个三位数可以分成三个步骤完成:
第一步确定百位上的数字,从5个数字中任选一个数字,共有5种选法; 第二步确定十位上的数字,由于数字允许重复,这仍有5种选法; 第三步确定十位上的数字,同理,它也有5种选法。 根据分步计数原理,得到组成的三位数的个数是:
N = 5 ×5 ×5 = 53 = 125
答:可以组成125个三位数。例3 要从甲、乙、丙3名工人中选2名分别上日班和晚班,有多少种不同的选法?解:安排出日晚班可分两个步骤完成:
第一步:从3名工人中选1人上日班,有3种选法。由分步计数原理得 3 × 2= 6答:共有 6 种选法。第二步:从剩余的2名工人中选1人上晚班,只有2种选法。两个原理区别 分类计数原理与分步计数原理,回答的都是有关做一件事的不同方法种数的问题。区别在于:分类计数原理针对的是“分类”问题,其中各种方法相互独立,用其中任何一种方法都可以做完这件事;分步计数原理针对的是“分步”问题,各个步骤中的方法相互依存,只有各个步骤都完成才算做完这件事。 1. 一件工作可以用两种方法完成。有5人会用第一种方法完成,另有4人会用第二种方法完成。选出一个人来完成这件工作,共有多少种选法?
2.乘积( a1+ a 2+ a 3 )( b1 + b 2 + b3 + b4 )(c1 + c2 + c3 + c4 + c5 )展开后共有项? 4 + 5 = 93×4×5=60练习2:1、把四封不同的信任意投入三个信箱中,不同投法种数是( )
A. 12 B.64 C.81 D.72、火车上有10名乘客,沿途有5个车站,乘客下车的可能方式有 ( )种
A. 510 B. 105 C. 50 D. 以上都不对练习1:CA总结:
1.分类计数原理:做一件事,完成它可以有 n 类办法,在第一类办法中有m1种不同的方法,在第一类办法中有m2种不同的方法,… …,在第n类办法中有mn种不同的方法。那麽完成这件事共有 N= m1+ m2+… …+ mn 种不同的方法。
分步计数原理:做一件事,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,… …,做第n步有mn种不同的方法。那麽完成这件事共有 N= m1× m2×… …×mn 种不同的方法。
2.分类计数原理和分步计数原理的
共同点:都是把一个事件分解成若干个分事件来完成;
不同点:前者分类,后者分步;如果分事件相互独立,分类完
备,就用分类计数原理;如果分事件相互关联,缺一
不可,就用分步计数原理。
