分类记数原理与分步记数原理[下学期]
图片预览






文档简介
课件17张PPT。分类记数原理与分步记数原理问题 1. 从临海到北京,可以乘火车,也可以乘汽车,还可以乘轮船。一天中,火车有4 班, 汽车有2班,轮船有3班。那么一天中乘坐这些交通工具从临海到北京共有多少种不同的走法?
分析: 从临海到北京有3 类不同的方法,
第一类方法, 乘火车,有4 种方法;
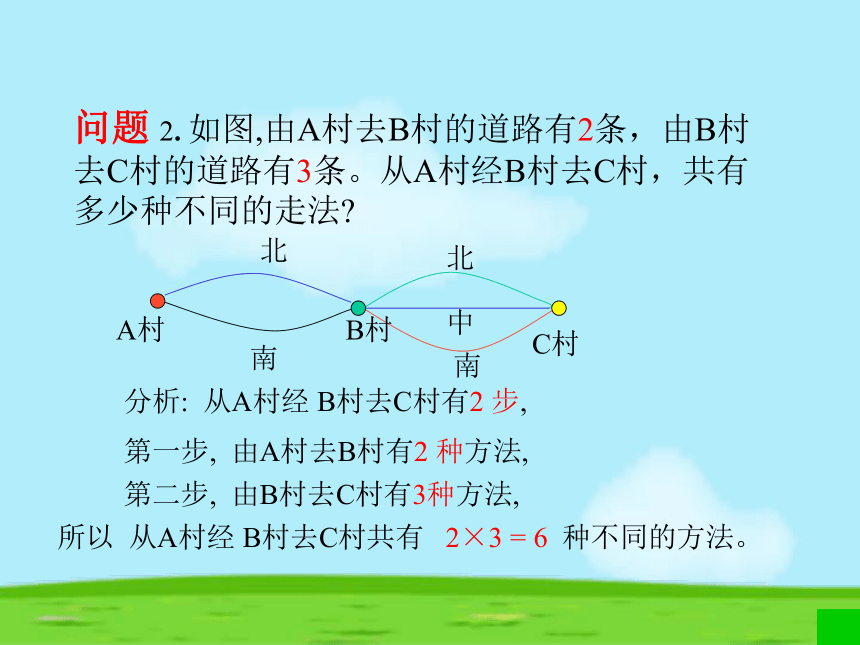
所以 从临海到北京共有 4 + 2 + 3 = 9 种方法。 第二类方法, 乘汽车,有2 种方法;第三类方法, 乘轮船, 有3 种方法;问题 2. 如图,由A村去B村的道路有2条,由B村去C村的道路有3条。从A村经B村去C村,共有多少种不同的走法?
A村B村C村北南中北南 分析: 从A村经 B村去C村有2 步,
第一步, 由A村去B村有2 种方法,第二步, 由B村去C村有3种方法,所以 从A村经 B村去C村共有 2×3 = 6 种不同的方法。问题3.一个口袋内装有5个小球,另一个口袋内装有4 个小球,所有这些小球的颜色互不相同.
(1)从两个口袋内任取一个小球,有多少种不同的取法?
(2)从两个口袋内各取一个小球,有多少种不同的取法?分类记数原理 做一件事情,完成它可以有n类办法,在第一类办法中有m1种不同的方法,在第二类办法中有m2种不同的方法,……,在第n类办法中有mn种不同的方法。那么完成这件事共有
N=m1+m2+…+mn
种不同的方法。
分步记数原理 做一件事情,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,……,做第n步有mn种不同的方法,那么完成这件事有
N=m1×m2×…×mn
种不同的方法。
例题1.书架上的第一层放有4本不同的计算机书,第二层放有3本不同的文艺书,第3层放有2本不同的体育书。
(1)从书架上任取1本书,有多少种不同的取法?(2)从书架的第1、2、3层各取1本书,有多少种不同的取法?
例题
2. 某班级有男三好学生5人,女三好学生4人。
(1)从中任选一人去领奖, 有多少种不同的选法?
(2) 从中任选男、女三好学生各一人去参加座谈会,有多少种不同的选法?
分析: (1) 完成从三好学生中任选一人去领奖这件事,共有2类办法,
第一类办法, 从男三好学生中任选一人, 共有 m1 = 5 种不同的方法;
第二类办法, 从女三好学生中任选一人, 共有 m2 = 4 种不同的方法;
所以, 根据加法原理, 得到不同选法种数共有 N = 5 + 4 = 9 种。
例题
2. 某班级有男三好学生5人,女三好学生4人。
(1)从中任选一人去领奖, 有多少种不同的选法?
(2) 从中任选男、女三好学生各一人去参加座谈会,有多少种不同的选法?
分析: (2) 完成从三好学生中任选男、女各一人去参加座谈会这件事, 需分2步完成,
第一步, 选一名男三好学生,有 m1 = 5 种方法;
第二步, 选一名女三好学生,有 m2 = 4 种方法;
所以, 根据乘法原理, 得到不同选法种数共有 N = 5 × 4 = 20 种。
点评: 解题的关键是从总体上看做这件事情是“分类完成”,还是“分步完成”。“分类完成”用“加法原理”;“分步完成”用“乘法原理”。
1. 分类计数原理和分步计数原理的共同点是什么?不同点什么?答: 共同点是, 它们都是研究完成一件事情, 共有多少种不同的方法。
不同点是, 它们研究完成一件事情的方式不同, 加法原理是“分类完成”, 即任何一类办法中的任何一个方法都能完成这件事。乘法原理是“分步完成”, 即这些方法需要分步,各个步骤顺次相依,且每一步都完成了,才能完成这件事情。这也是本节课的重点。2. 何时用分类法数原理、分步计数原理呢?
答:完成一件事情有n类方法,若每一类方法中的任何一种方法均能将这件事情从头至尾完成,则计算完成这件事情的方法总数用分类法数原理。
完成一件事情有n个步骤,若每一步的任何一种方法只能完成这件事的一部分,并且必须且只需完成互相独立的这n步后,才能完成这件事,则计算完成这件事的方法总数用分步计数原理。
例3
(1)4名同学选报跑步、跳高、跳远三个项目,每人报一项,
共有多少种不同的方法?(2)4名同学争夺跑步、跳高、跳远三个项目的冠军,共有几
种不同的结果?例4
4封信放入6个邮箱寄出,共有多少种不同的方法?例5
要从甲、乙、丙3名工人中选出2名分别上日班和晚班,有
多少种不同的方法?㈣ 课堂练习
1 .如图,要给地图A、B、C、D四个区域分别涂上3种不同颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同的颜色,不同的涂色方案有多少种?
㈣ 课堂练习
1 .如图,要给地图A、B、C、D四个区域分别涂上3种不同颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同的颜色,不同的涂色方案有多少种?
解: 按地图A、B、C、D四个区域依次分四步完成,
第一步, m1 = 3 种,
第二步, m2 = 2 种,
第三步, m3 = 1 种,
第四步, m4 = 1 种,
所以根据乘法原理, 得到不同的涂色方案种数共有 N = 3 × 2 ×1×1 = 6 种。
㈣ 课堂练习
1 .如图,要给地图A、B、C、D四个区域分别涂上3种不同颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同的颜色,不同的涂色方案有多少种?
问: 若用2色、3色、4色、5色等,结果又怎样呢? 答:它们的涂色方案种数分别是 0, 4×3×2×2 = 48, 5×4×3×3 = 180种等。
分析: 从临海到北京有3 类不同的方法,
第一类方法, 乘火车,有4 种方法;
所以 从临海到北京共有 4 + 2 + 3 = 9 种方法。 第二类方法, 乘汽车,有2 种方法;第三类方法, 乘轮船, 有3 种方法;问题 2. 如图,由A村去B村的道路有2条,由B村去C村的道路有3条。从A村经B村去C村,共有多少种不同的走法?
A村B村C村北南中北南 分析: 从A村经 B村去C村有2 步,
第一步, 由A村去B村有2 种方法,第二步, 由B村去C村有3种方法,所以 从A村经 B村去C村共有 2×3 = 6 种不同的方法。问题3.一个口袋内装有5个小球,另一个口袋内装有4 个小球,所有这些小球的颜色互不相同.
(1)从两个口袋内任取一个小球,有多少种不同的取法?
(2)从两个口袋内各取一个小球,有多少种不同的取法?分类记数原理 做一件事情,完成它可以有n类办法,在第一类办法中有m1种不同的方法,在第二类办法中有m2种不同的方法,……,在第n类办法中有mn种不同的方法。那么完成这件事共有
N=m1+m2+…+mn
种不同的方法。
分步记数原理 做一件事情,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,……,做第n步有mn种不同的方法,那么完成这件事有
N=m1×m2×…×mn
种不同的方法。
例题1.书架上的第一层放有4本不同的计算机书,第二层放有3本不同的文艺书,第3层放有2本不同的体育书。
(1)从书架上任取1本书,有多少种不同的取法?(2)从书架的第1、2、3层各取1本书,有多少种不同的取法?
例题
2. 某班级有男三好学生5人,女三好学生4人。
(1)从中任选一人去领奖, 有多少种不同的选法?
(2) 从中任选男、女三好学生各一人去参加座谈会,有多少种不同的选法?
分析: (1) 完成从三好学生中任选一人去领奖这件事,共有2类办法,
第一类办法, 从男三好学生中任选一人, 共有 m1 = 5 种不同的方法;
第二类办法, 从女三好学生中任选一人, 共有 m2 = 4 种不同的方法;
所以, 根据加法原理, 得到不同选法种数共有 N = 5 + 4 = 9 种。
例题
2. 某班级有男三好学生5人,女三好学生4人。
(1)从中任选一人去领奖, 有多少种不同的选法?
(2) 从中任选男、女三好学生各一人去参加座谈会,有多少种不同的选法?
分析: (2) 完成从三好学生中任选男、女各一人去参加座谈会这件事, 需分2步完成,
第一步, 选一名男三好学生,有 m1 = 5 种方法;
第二步, 选一名女三好学生,有 m2 = 4 种方法;
所以, 根据乘法原理, 得到不同选法种数共有 N = 5 × 4 = 20 种。
点评: 解题的关键是从总体上看做这件事情是“分类完成”,还是“分步完成”。“分类完成”用“加法原理”;“分步完成”用“乘法原理”。
1. 分类计数原理和分步计数原理的共同点是什么?不同点什么?答: 共同点是, 它们都是研究完成一件事情, 共有多少种不同的方法。
不同点是, 它们研究完成一件事情的方式不同, 加法原理是“分类完成”, 即任何一类办法中的任何一个方法都能完成这件事。乘法原理是“分步完成”, 即这些方法需要分步,各个步骤顺次相依,且每一步都完成了,才能完成这件事情。这也是本节课的重点。2. 何时用分类法数原理、分步计数原理呢?
答:完成一件事情有n类方法,若每一类方法中的任何一种方法均能将这件事情从头至尾完成,则计算完成这件事情的方法总数用分类法数原理。
完成一件事情有n个步骤,若每一步的任何一种方法只能完成这件事的一部分,并且必须且只需完成互相独立的这n步后,才能完成这件事,则计算完成这件事的方法总数用分步计数原理。
例3
(1)4名同学选报跑步、跳高、跳远三个项目,每人报一项,
共有多少种不同的方法?(2)4名同学争夺跑步、跳高、跳远三个项目的冠军,共有几
种不同的结果?例4
4封信放入6个邮箱寄出,共有多少种不同的方法?例5
要从甲、乙、丙3名工人中选出2名分别上日班和晚班,有
多少种不同的方法?㈣ 课堂练习
1 .如图,要给地图A、B、C、D四个区域分别涂上3种不同颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同的颜色,不同的涂色方案有多少种?
㈣ 课堂练习
1 .如图,要给地图A、B、C、D四个区域分别涂上3种不同颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同的颜色,不同的涂色方案有多少种?
解: 按地图A、B、C、D四个区域依次分四步完成,
第一步, m1 = 3 种,
第二步, m2 = 2 种,
第三步, m3 = 1 种,
第四步, m4 = 1 种,
所以根据乘法原理, 得到不同的涂色方案种数共有 N = 3 × 2 ×1×1 = 6 种。
㈣ 课堂练习
1 .如图,要给地图A、B、C、D四个区域分别涂上3种不同颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同的颜色,不同的涂色方案有多少种?
问: 若用2色、3色、4色、5色等,结果又怎样呢? 答:它们的涂色方案种数分别是 0, 4×3×2×2 = 48, 5×4×3×3 = 180种等。
