排列与组合[上学期]
图片预览






文档简介
课件15张PPT。 第九章 排列、组合、二项式定理一 排列与组合第一课 基本原理例1 从甲地到乙地,可以乘火车,也可以乘汽车,还可以乘轮船。一天中,火车有4班,汽车有2班,轮船有3班。那麽,一天中乘坐这些交通工具从甲地到乙地共有多少种不同的走法?解:因为一天中乘火车有4种走法,乘汽车有2种走法,乘轮船有3种走法,每一种走法都可以从甲地到乙地,因此,一天中乘坐这些交通工具从甲地到乙地共有 4+2+3=9 种不同的走法。
加法原理: 做一件事,完成它可以有 n 类办法,在第一类办法中有m1种不同的方法,在第二类办法中有m2种不同的方法,… …,在第n类办法中有mn种不同的方法。那么完成这件事共有 N= m1+ m2+… …+ mn 种不同的方法。
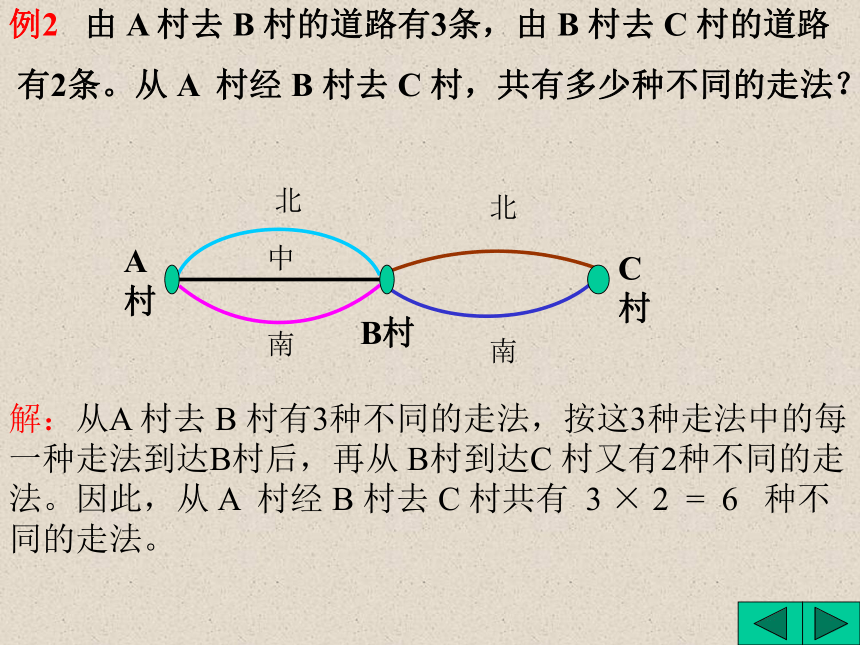
例2 由 A 村去 B 村的道路有3条,由 B 村去 C 村的道路
有2条。从 A 村经 B 村去 C 村,共有多少种不同的走法?解:从A 村去 B 村有3种不同的走法,按这3种走法中的每一种走法到达B村后,再从 B村到达C 村又有2种不同的走法。因此,从 A 村经 B 村去 C 村共有 3 × 2 = 6 种不同的走法。乘法原理: 做一件事,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,… …,做第n步有mn种不同的方法。那么完成这件事共有 N= m1× m2×… …×mn 种不同的方法。
加法原理:做一件事,完成它可以有 n 类办法,在第一类办法中有m1种不同的方法,在第一类办法中有m2种不同的方法,… …,在第n类办法中有mn种不同的方法。那麽完成这件事共有 N= m1+ m2+… …+ mn 种不同的方法。
乘法原理:做一件事,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,… …,做第n步有mn种不同的方法。那麽完成这件事共有 N= m1× m2×… …×mn 种不同的方法。两个原理的
共同点:
不同点:
都是把一个事件分解成若干个分事件来完成;前者分类,后者分步;
如果分事件相互独立,分类完备,就用加法原理;
如果分事件相互关联,缺一不可,就用乘法原理。
例1 书架上层放有 6 本不同的数学书,下层放有 5 本不同的语文书。
⑴从中任取一本,共有多少种不同的取法?
⑵从中任取数学书与语文书各一本,共有多少种不同的取法?解:⑴从书架上任取一本书,有两类办法:
第一类办法是从上层取数学书,可以从 6 本书中任取一本,有 6 种取法;
第二类办法是从下层取语文书,可以从5本书中任取一本,有5 种取法。
根据加法原理,得到不同的取法的种数是:
N = m1+ m2 = 6+5=11
答:从书架上任取一本书,有11种不同的取法。解: ⑵从书架上任取数学书与语文书各一本,可以分成两个步骤完成:
第一步取一本数学书,有6种方法;第二步取一本语文书,有5种方法。根据乘法原理,得到不同的取法的种数是:
N= m1× m2 = 6×5 = 30
答: 从书架上取数学书与语文书各一本,共有30 种不同的取法。
例1 书架上层放有 6 本不同的数学书,下层放有 5 本不同的语文书。
⑴从中任取一本,共有多少种不同的取法?
⑵从中任取数学书与语文书各一本,共有多少种不同的取法?
例2 有数字 1,2,3,4,5 可以组成多少个三位数(各位上的数字许重复)?解:要组成一个三位数可以分成三个步骤完成:
第一步确定百位上的数字,从5个数字中任选一个数字,共有5种选法;
第二步确定十位上的数字,由于数字允许重复,这仍有5种选法;
第二步确定十位上的数字,同理,它也有5种选法。
根据乘法原理,得到组成的三位数的个数是:
N = 5 ×5 ×5 = 53 = 125
答:可以组成125个三位数。例3 有不同的语文书9本,不同的数学书7本,不同的物理书5本,从中任取两种不同类的书,共有多少种不同的取法?解:每次取出的两本书中:
含 1 本语文书和 1 本数学书的共有 9 × 7 = 63 种取法;
含 1 本数学书和 1 本物理书的共有 7 × 5 = 35 种取法;
含 1 本语文书和 1 本物理书的共有 9 × 5 = 45 种取法。
由加法原理得 63 + 35 + 45 = 143
答:共有 143 种取法。练习1:
1. 一件工作可以用两种方法完成。有5人会用第一种方法完成,另有4人会用第二种方法完成。选出一个人来完成这件工作,共有多少种选法?
2. 在读书活动中,一个学生要从2本科技书,2本政治书,3本文艺术里任选一本,共有多少种不同的选法?
3.乘积( a1+ a 2+ a 3 )( b1 + b 2 + b3 + b4 )(c1 + c2 + c3 + c4 +
c5 )展开后共有项?
4 + 5 = 92 + 2 + 3 = 73×4×5=60
练习题2:书架的上层放有 5 本不同的数学书,中层放有6本不同的语文书,下层放有4本不同的英语书,从中任取1 本书的不同取法的种数是 ( )
A. 5 + 6+4 = 15 B. 1 C. 6×5×4 = 120 D. 3A在上题中,如果从中任取3本,数学,语文,英语各一本,则不同取法的种数是 ( )
A. 1 + 1 + 1 = 3 B.5 + 6 + 4 =15 C. 5×6×4 = 120 D. 1C把四封信任意投入三个信箱中,不同投法种数是 ( )
A. 12 B.64 C.81 D.7C4 火车上有10名乘客,沿途有5个车站,乘客下车的可能方式有
( )种
A. 510 B. 105 C. 50 D. 以上都不对
A
总结:
1.加法原理:做一件事,完成它可以有 n 类办法,在第一类办法中有m1种不同的方法,在第一类办法中有m2种不同的方法,… …,在第n类办法中有mn种不同的方法。那麽完成这件事共有 N= m1+ m2+… …+ mn 种不同的方法。
乘法原理:做一件事,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,… …,做第n步有mn种不同的方法。那麽完成这件事共有 N= m1× m2×… …×mn 种不同的方法。
2.加法原理和乘法原理的
共同点:都是把一个事件分解成若干个分事件来完成;
不同点:前者分类,后者分步;如果分事件相互独立,分类完 备,就用加法原理;如果分事件相互关联,缺一不可, 就用乘法原理。作业:
第266页 6题 7题
补充题: 从2,3,5,7四个数字中任取两个用来做分子,分母。
①能得到几个不同的分数?
②其中有几个是真分数?几个假分数?课下练习题:
第266页 3题 5题
加法原理: 做一件事,完成它可以有 n 类办法,在第一类办法中有m1种不同的方法,在第二类办法中有m2种不同的方法,… …,在第n类办法中有mn种不同的方法。那么完成这件事共有 N= m1+ m2+… …+ mn 种不同的方法。
例2 由 A 村去 B 村的道路有3条,由 B 村去 C 村的道路
有2条。从 A 村经 B 村去 C 村,共有多少种不同的走法?解:从A 村去 B 村有3种不同的走法,按这3种走法中的每一种走法到达B村后,再从 B村到达C 村又有2种不同的走法。因此,从 A 村经 B 村去 C 村共有 3 × 2 = 6 种不同的走法。乘法原理: 做一件事,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,… …,做第n步有mn种不同的方法。那么完成这件事共有 N= m1× m2×… …×mn 种不同的方法。
加法原理:做一件事,完成它可以有 n 类办法,在第一类办法中有m1种不同的方法,在第一类办法中有m2种不同的方法,… …,在第n类办法中有mn种不同的方法。那麽完成这件事共有 N= m1+ m2+… …+ mn 种不同的方法。
乘法原理:做一件事,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,… …,做第n步有mn种不同的方法。那麽完成这件事共有 N= m1× m2×… …×mn 种不同的方法。两个原理的
共同点:
不同点:
都是把一个事件分解成若干个分事件来完成;前者分类,后者分步;
如果分事件相互独立,分类完备,就用加法原理;
如果分事件相互关联,缺一不可,就用乘法原理。
例1 书架上层放有 6 本不同的数学书,下层放有 5 本不同的语文书。
⑴从中任取一本,共有多少种不同的取法?
⑵从中任取数学书与语文书各一本,共有多少种不同的取法?解:⑴从书架上任取一本书,有两类办法:
第一类办法是从上层取数学书,可以从 6 本书中任取一本,有 6 种取法;
第二类办法是从下层取语文书,可以从5本书中任取一本,有5 种取法。
根据加法原理,得到不同的取法的种数是:
N = m1+ m2 = 6+5=11
答:从书架上任取一本书,有11种不同的取法。解: ⑵从书架上任取数学书与语文书各一本,可以分成两个步骤完成:
第一步取一本数学书,有6种方法;第二步取一本语文书,有5种方法。根据乘法原理,得到不同的取法的种数是:
N= m1× m2 = 6×5 = 30
答: 从书架上取数学书与语文书各一本,共有30 种不同的取法。
例1 书架上层放有 6 本不同的数学书,下层放有 5 本不同的语文书。
⑴从中任取一本,共有多少种不同的取法?
⑵从中任取数学书与语文书各一本,共有多少种不同的取法?
例2 有数字 1,2,3,4,5 可以组成多少个三位数(各位上的数字许重复)?解:要组成一个三位数可以分成三个步骤完成:
第一步确定百位上的数字,从5个数字中任选一个数字,共有5种选法;
第二步确定十位上的数字,由于数字允许重复,这仍有5种选法;
第二步确定十位上的数字,同理,它也有5种选法。
根据乘法原理,得到组成的三位数的个数是:
N = 5 ×5 ×5 = 53 = 125
答:可以组成125个三位数。例3 有不同的语文书9本,不同的数学书7本,不同的物理书5本,从中任取两种不同类的书,共有多少种不同的取法?解:每次取出的两本书中:
含 1 本语文书和 1 本数学书的共有 9 × 7 = 63 种取法;
含 1 本数学书和 1 本物理书的共有 7 × 5 = 35 种取法;
含 1 本语文书和 1 本物理书的共有 9 × 5 = 45 种取法。
由加法原理得 63 + 35 + 45 = 143
答:共有 143 种取法。练习1:
1. 一件工作可以用两种方法完成。有5人会用第一种方法完成,另有4人会用第二种方法完成。选出一个人来完成这件工作,共有多少种选法?
2. 在读书活动中,一个学生要从2本科技书,2本政治书,3本文艺术里任选一本,共有多少种不同的选法?
3.乘积( a1+ a 2+ a 3 )( b1 + b 2 + b3 + b4 )(c1 + c2 + c3 + c4 +
c5 )展开后共有项?
4 + 5 = 92 + 2 + 3 = 73×4×5=60
练习题2:书架的上层放有 5 本不同的数学书,中层放有6本不同的语文书,下层放有4本不同的英语书,从中任取1 本书的不同取法的种数是 ( )
A. 5 + 6+4 = 15 B. 1 C. 6×5×4 = 120 D. 3A在上题中,如果从中任取3本,数学,语文,英语各一本,则不同取法的种数是 ( )
A. 1 + 1 + 1 = 3 B.5 + 6 + 4 =15 C. 5×6×4 = 120 D. 1C把四封信任意投入三个信箱中,不同投法种数是 ( )
A. 12 B.64 C.81 D.7C4 火车上有10名乘客,沿途有5个车站,乘客下车的可能方式有
( )种
A. 510 B. 105 C. 50 D. 以上都不对
A
总结:
1.加法原理:做一件事,完成它可以有 n 类办法,在第一类办法中有m1种不同的方法,在第一类办法中有m2种不同的方法,… …,在第n类办法中有mn种不同的方法。那麽完成这件事共有 N= m1+ m2+… …+ mn 种不同的方法。
乘法原理:做一件事,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,… …,做第n步有mn种不同的方法。那麽完成这件事共有 N= m1× m2×… …×mn 种不同的方法。
2.加法原理和乘法原理的
共同点:都是把一个事件分解成若干个分事件来完成;
不同点:前者分类,后者分步;如果分事件相互独立,分类完 备,就用加法原理;如果分事件相互关联,缺一不可, 就用乘法原理。作业:
第266页 6题 7题
补充题: 从2,3,5,7四个数字中任取两个用来做分子,分母。
①能得到几个不同的分数?
②其中有几个是真分数?几个假分数?课下练习题:
第266页 3题 5题
