沪科版八年级下册19.4 综合与实践 多边形的镶嵌课件(共15张PPT)
文档属性
| 名称 | 沪科版八年级下册19.4 综合与实践 多边形的镶嵌课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 202.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-10 08:26:52 | ||
图片预览



文档简介
(共15张PPT)
三角形中位线构造和运用
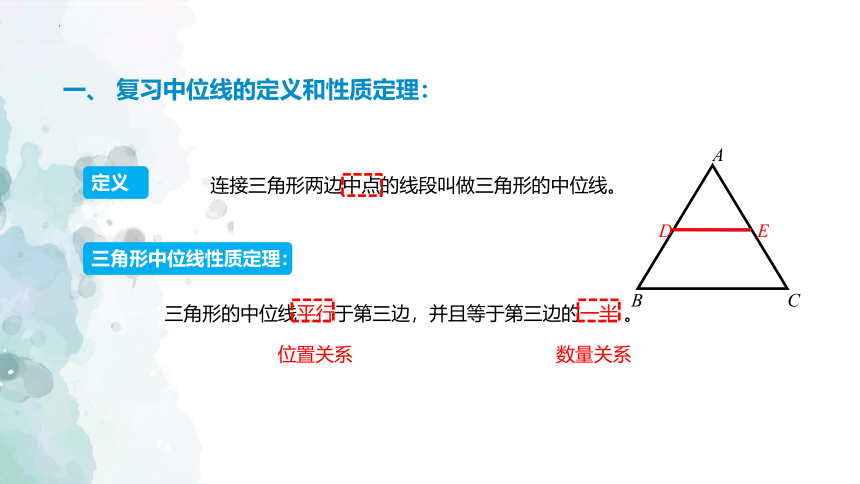
知识梳理
连接三角形两边中点的线段叫做三角形的中位线。
三角形的中位线平行于第三边,并且等于第三边的一半 。
定义
三角形中位线性质定理:
A
B
C
E
D
一、 复习中位线的定义和性质定理:
位置关系
数量关系
二、中位线的五种构造方法:
1. 直接连线法: 直接连接两点构造三角形的中位线。
2. 利用角平分线+垂直:根据等腰三角形底边上三线合一的性质,角平分线和垂线共线时,这条线也同为中线。
3. 倍长法:延长线段至其两倍长度构造出中位线。
4. 已知一边中点,取另一边中点构造三角形的中位线。
5. 已知两边中点,取第三边中点构造三角形的中位线。
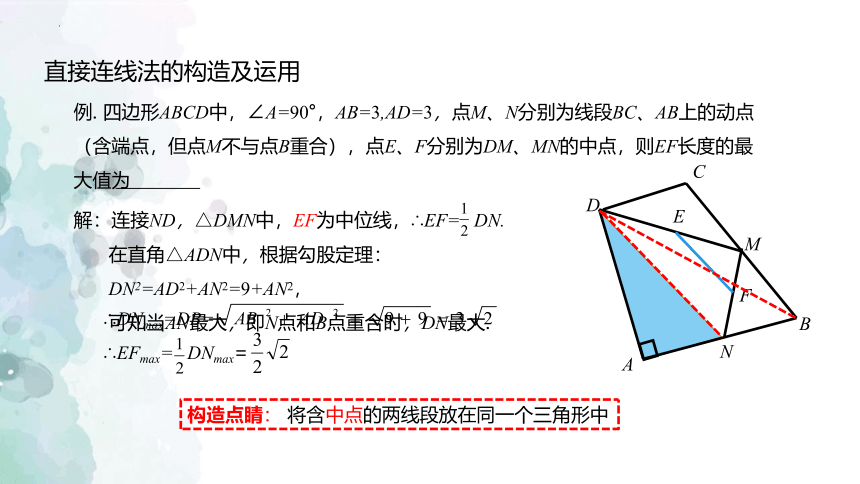
直接连线法的构造及运用
例. 四边形ABCD中,∠A=90°,AB=3,AD=3,点M、N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E、F分别为DM、MN的中点,则EF长度的最大值为
分析
E为DM中点,F为MN中点
连接DN,构造出中位线EF
EF最大值转化为DN最大值
△DAN是直角三角形
勾股定理
当N点在B点时,DN最大
勾股定理求DB,得EF最大值
勾股定理
D
A
B
N
C
F
E
M
直接连线法的构造及运用
构造点睛: 将含中点的两线段放在同一个三角形中
在直角△ADN中,根据勾股定理:DN2=AD2+AN2=9+AN2,
可知当AN最大,即N点和B点重合时,DN最大.
解:连接ND,△DMN中,EF为中位线,∴EF= DN.
例. 四边形ABCD中,∠A=90°,AB=3,AD=3,点M、N分别为线段BC、AB上的动点(含端点,但点M不与点B重合),点E、F分别为DM、MN的中点,则EF长度的最大值为
∴DNmax=DB=
∴EFmax= DNmax=
D
A
B
N
C
F
E
M
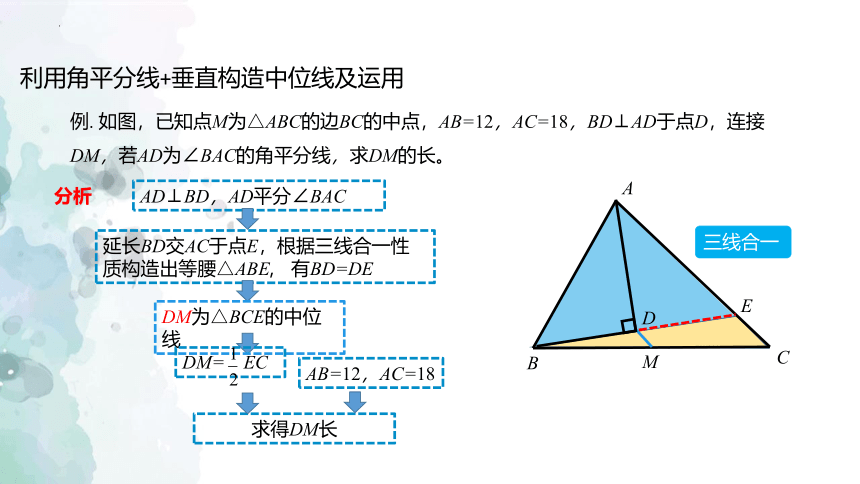
利用角平分线+垂直构造中位线及运用
例. 如图,已知点M为△ABC的边BC的中点,AB=12,AC=18,BD⊥AD于点D,连接DM,若AD为∠BAC的角平分线,求DM的长。
分析
AD⊥BD,AD平分∠BAC
延长BD交AC于点E,根据三线合一性质构造出等腰△ABE, 有BD=DE
求得DM长
三线合一
DM为△BCE的中位线
A
B
C
D
M
AB=12,AC=18
DM= EC
E
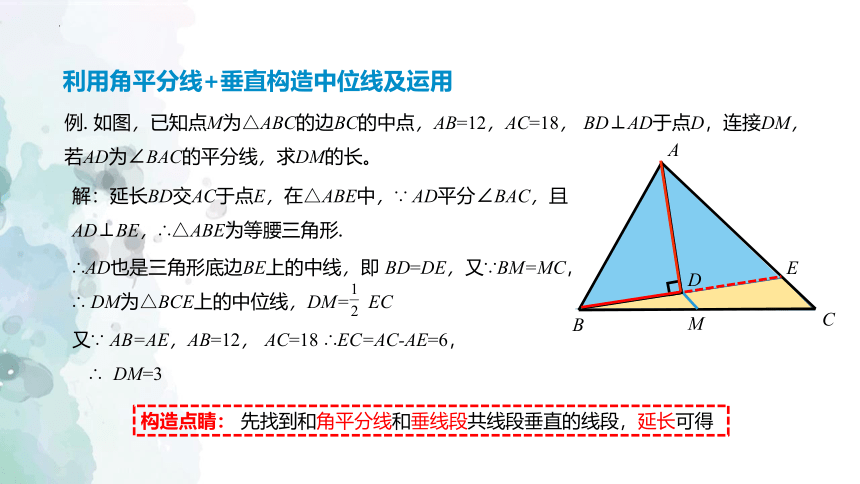
例. 如图,已知点M为△ABC的边BC的中点,AB=12,AC=18, BD⊥AD于点D,连接DM,若AD为∠BAC的平分线,求DM的长。
又∵ AB=AE,AB=12, AC=18 ∴EC=AC-AE=6,
∴ DM=3
利用角平分线+垂直构造中位线及运用
构造点睛: 先找到和角平分线和垂线段共线段垂直的线段,延长可得
解:延长BD交AC于点E,在△ABE中,∵ AD平分∠BAC,且AD⊥BE,∴△ABE为等腰三角形.
∴AD也是三角形底边BE上的中线,即 BD=DE,又∵BM=MC,
∴ DM为△BCE上的中位线,DM= EC
A
B
C
D
M
E
倍长法构造及运用
例. 在锐角△ABC中,AD为BC中线,F为AD延长线上一点且AD=2DF,E为BD中点,
求证:AC=2EF
G
A
B
D
E
F
C
分析
E为BD中点,D为BC中点
倍长DF到点G,使得GF=FD,连接BG,构造出中位线EF
探究BG和AC关系
得到△GDB和△ADC全等
AC=2EF
AD=2DF
AD为中线
全等三角形
EF= BG
∴ BG=AC, ∴ AC=2EF
倍长法构造及运用
构造点睛: 把和中点所在线段有关的三角形中的另一条线段倍长
∵AD=2DF, DG=2DF,
∴在△BDG和△CDA中,
DG=DA,∠CDA=∠BDG, BD=CD
∴△CDA≌△BDG (SAS)
A
G
B
D
E
F
C
例. 在锐角△ABC中,AD为BC中线,F为AD延长线上一点且AD=2DF,E为BD中点,
求证:AC=2EF
证明:延长DF到G点, 使得FG=DF,连接BG,
可得在△BDG中,EF为中位线,∴EF= BG
已知一边中点,取另一边中点构造中位线及运用
例. 如图,在△ABC中, AB=AC, AD⊥BC于点D,点P是AD的中点,延长BP交AC于点N, 求证:AC=3AN
A
D
N
B
C
P
分析
题干条件AB=AC,AD⊥BC
根据三线合一性质得出BD=DC
取BN中点E,连接DE,构造△BCN的中位线ED
P是中点
三线合一
全等三角形
AN=ED
ED∥NC
E
ED= NC
猜想并证明△EDP和△NAP全等
AC=3AN
已知一边中点,取另一边中点构造中位线及运用
构造点睛: 找到含有中点的线段和要证结论中的线段同时有关的三角形,取另一边中点
由DE∥NC可得∠EDP=∠NAP
DP=AP (P为中点)
∠EPD=∠NPA ∴ △EPD≌△NPA (ASA)
例. 如图,在△ABC中, AB=AC, AD⊥BC于点D,点P是AD的中点,延长BP交AC于点N, 求证:AC=3AN
证明:∵AB=AC, AD⊥BC, ∴BD=CD, 取NB的中点E, 连接ED, 可知ED为△BNC的中位线,∴DE∥NC,ED= NC
∴ED=AN, 又ED= NC,∴ AN= NC, ∴ AC=3AN
A
D
N
B
C
P
E
已知两边中点,取第三边中点构造中位线及运用
N
D
A
B
F
E
C
M
分析
从CA=CB,CE=CF得到AE=BF
根据两三角形共边AB,取中点G,构造中位线NG和MG
△NGM为等腰直角三角形
△ABC为等腰直角三角形
等腰直角三角形
NG∥AC,GM∥BC,可得∠BGN=∠AGM=45°
例. 如图,在△ABC中,∠C=90°,CA=CB, E、F分别为CA、CB上一点,且有CE=CF, M、N分别为AF、BE 的中点,求证:AE= MN
G
根据等腰三角形的边角关系可证命题
NG= AE,MG= BF
已知两边中点,取第三边中点构造及运用
构造点睛: 找到含中点的线段和要证命题中有关的线段组成的三角形,取第三边中点!
∵CE=CF, ∴BC-CF=AC-CE,即BF=AE
证明:∵∠C=90°,CA=CB,∴∠BAC=∠ABC=45°
例. 如图,在△ABC中,∠C=90°,CA=CB, E、F分别为CA、CB上一点,CE=CF, M、N分别为AF、BE 的中点,求证:AE= MN
取AB中点G, 连接NG、MG, ∵NG、MG分别为△ABE和△ABF的中位线,∴ NG= AE , ∠BGN=∠BAC=45°, MG= BF,∠AGM=∠ABC=45°,
又∵BF=AE, ∴NG=MG,
∴∠NGM=180°-∠AGM-∠BGN=90°,
∴△MGN为等腰直角三角形 ∴MN= NG, 又∵NG= AE
∴ AE=2NG= MN
N
D
A
B
F
E
C
M
G
1.中线的定义:
2.直角三角形斜边中线定理:
3.应用:构造直角三角形斜边上的中线与中位线的综合应用, 对于复杂几何图形,分解成简单图形解决问题。
三角形中一个顶点到它对边中点的线段. 如图
直角三角形斜边上的中线等于斜边的一半
A
C
B
D
C
B
A
D
4.中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半
D为BC中点,则AD为△ABC的中线
如图:Rt△ACD中,CD为中线,则CD= AB
∟
总结
再 见
三角形中位线构造和运用
知识梳理
连接三角形两边中点的线段叫做三角形的中位线。
三角形的中位线平行于第三边,并且等于第三边的一半 。
定义
三角形中位线性质定理:
A
B
C
E
D
一、 复习中位线的定义和性质定理:
位置关系
数量关系
二、中位线的五种构造方法:
1. 直接连线法: 直接连接两点构造三角形的中位线。
2. 利用角平分线+垂直:根据等腰三角形底边上三线合一的性质,角平分线和垂线共线时,这条线也同为中线。
3. 倍长法:延长线段至其两倍长度构造出中位线。
4. 已知一边中点,取另一边中点构造三角形的中位线。
5. 已知两边中点,取第三边中点构造三角形的中位线。
直接连线法的构造及运用
例. 四边形ABCD中,∠A=90°,AB=3,AD=3,点M、N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E、F分别为DM、MN的中点,则EF长度的最大值为
分析
E为DM中点,F为MN中点
连接DN,构造出中位线EF
EF最大值转化为DN最大值
△DAN是直角三角形
勾股定理
当N点在B点时,DN最大
勾股定理求DB,得EF最大值
勾股定理
D
A
B
N
C
F
E
M
直接连线法的构造及运用
构造点睛: 将含中点的两线段放在同一个三角形中
在直角△ADN中,根据勾股定理:DN2=AD2+AN2=9+AN2,
可知当AN最大,即N点和B点重合时,DN最大.
解:连接ND,△DMN中,EF为中位线,∴EF= DN.
例. 四边形ABCD中,∠A=90°,AB=3,AD=3,点M、N分别为线段BC、AB上的动点(含端点,但点M不与点B重合),点E、F分别为DM、MN的中点,则EF长度的最大值为
∴DNmax=DB=
∴EFmax= DNmax=
D
A
B
N
C
F
E
M
利用角平分线+垂直构造中位线及运用
例. 如图,已知点M为△ABC的边BC的中点,AB=12,AC=18,BD⊥AD于点D,连接DM,若AD为∠BAC的角平分线,求DM的长。
分析
AD⊥BD,AD平分∠BAC
延长BD交AC于点E,根据三线合一性质构造出等腰△ABE, 有BD=DE
求得DM长
三线合一
DM为△BCE的中位线
A
B
C
D
M
AB=12,AC=18
DM= EC
E
例. 如图,已知点M为△ABC的边BC的中点,AB=12,AC=18, BD⊥AD于点D,连接DM,若AD为∠BAC的平分线,求DM的长。
又∵ AB=AE,AB=12, AC=18 ∴EC=AC-AE=6,
∴ DM=3
利用角平分线+垂直构造中位线及运用
构造点睛: 先找到和角平分线和垂线段共线段垂直的线段,延长可得
解:延长BD交AC于点E,在△ABE中,∵ AD平分∠BAC,且AD⊥BE,∴△ABE为等腰三角形.
∴AD也是三角形底边BE上的中线,即 BD=DE,又∵BM=MC,
∴ DM为△BCE上的中位线,DM= EC
A
B
C
D
M
E
倍长法构造及运用
例. 在锐角△ABC中,AD为BC中线,F为AD延长线上一点且AD=2DF,E为BD中点,
求证:AC=2EF
G
A
B
D
E
F
C
分析
E为BD中点,D为BC中点
倍长DF到点G,使得GF=FD,连接BG,构造出中位线EF
探究BG和AC关系
得到△GDB和△ADC全等
AC=2EF
AD=2DF
AD为中线
全等三角形
EF= BG
∴ BG=AC, ∴ AC=2EF
倍长法构造及运用
构造点睛: 把和中点所在线段有关的三角形中的另一条线段倍长
∵AD=2DF, DG=2DF,
∴在△BDG和△CDA中,
DG=DA,∠CDA=∠BDG, BD=CD
∴△CDA≌△BDG (SAS)
A
G
B
D
E
F
C
例. 在锐角△ABC中,AD为BC中线,F为AD延长线上一点且AD=2DF,E为BD中点,
求证:AC=2EF
证明:延长DF到G点, 使得FG=DF,连接BG,
可得在△BDG中,EF为中位线,∴EF= BG
已知一边中点,取另一边中点构造中位线及运用
例. 如图,在△ABC中, AB=AC, AD⊥BC于点D,点P是AD的中点,延长BP交AC于点N, 求证:AC=3AN
A
D
N
B
C
P
分析
题干条件AB=AC,AD⊥BC
根据三线合一性质得出BD=DC
取BN中点E,连接DE,构造△BCN的中位线ED
P是中点
三线合一
全等三角形
AN=ED
ED∥NC
E
ED= NC
猜想并证明△EDP和△NAP全等
AC=3AN
已知一边中点,取另一边中点构造中位线及运用
构造点睛: 找到含有中点的线段和要证结论中的线段同时有关的三角形,取另一边中点
由DE∥NC可得∠EDP=∠NAP
DP=AP (P为中点)
∠EPD=∠NPA ∴ △EPD≌△NPA (ASA)
例. 如图,在△ABC中, AB=AC, AD⊥BC于点D,点P是AD的中点,延长BP交AC于点N, 求证:AC=3AN
证明:∵AB=AC, AD⊥BC, ∴BD=CD, 取NB的中点E, 连接ED, 可知ED为△BNC的中位线,∴DE∥NC,ED= NC
∴ED=AN, 又ED= NC,∴ AN= NC, ∴ AC=3AN
A
D
N
B
C
P
E
已知两边中点,取第三边中点构造中位线及运用
N
D
A
B
F
E
C
M
分析
从CA=CB,CE=CF得到AE=BF
根据两三角形共边AB,取中点G,构造中位线NG和MG
△NGM为等腰直角三角形
△ABC为等腰直角三角形
等腰直角三角形
NG∥AC,GM∥BC,可得∠BGN=∠AGM=45°
例. 如图,在△ABC中,∠C=90°,CA=CB, E、F分别为CA、CB上一点,且有CE=CF, M、N分别为AF、BE 的中点,求证:AE= MN
G
根据等腰三角形的边角关系可证命题
NG= AE,MG= BF
已知两边中点,取第三边中点构造及运用
构造点睛: 找到含中点的线段和要证命题中有关的线段组成的三角形,取第三边中点!
∵CE=CF, ∴BC-CF=AC-CE,即BF=AE
证明:∵∠C=90°,CA=CB,∴∠BAC=∠ABC=45°
例. 如图,在△ABC中,∠C=90°,CA=CB, E、F分别为CA、CB上一点,CE=CF, M、N分别为AF、BE 的中点,求证:AE= MN
取AB中点G, 连接NG、MG, ∵NG、MG分别为△ABE和△ABF的中位线,∴ NG= AE , ∠BGN=∠BAC=45°, MG= BF,∠AGM=∠ABC=45°,
又∵BF=AE, ∴NG=MG,
∴∠NGM=180°-∠AGM-∠BGN=90°,
∴△MGN为等腰直角三角形 ∴MN= NG, 又∵NG= AE
∴ AE=2NG= MN
N
D
A
B
F
E
C
M
G
1.中线的定义:
2.直角三角形斜边中线定理:
3.应用:构造直角三角形斜边上的中线与中位线的综合应用, 对于复杂几何图形,分解成简单图形解决问题。
三角形中一个顶点到它对边中点的线段. 如图
直角三角形斜边上的中线等于斜边的一半
A
C
B
D
C
B
A
D
4.中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半
D为BC中点,则AD为△ABC的中线
如图:Rt△ACD中,CD为中线,则CD= AB
∟
总结
再 见
