线性回归[上学期]
图片预览






文档简介
课件28张PPT。线性回归
由身高预测体重(kg):
体重预测值(cm)
=0.72kg/cm×身高 - 58.5kg.一、课题引入1、两个变量之间的关系:函数关系 非确定关系 自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系. 二、新课讲解:2、相关关系与函数关系的异同点: (一)相同点:均是指两个变量的关系。 (二)不同点:
1、函数关系是自变量与因变量之间 的关系,这种关系是两个非随机变量的关系;而相关关系是非随机变量与随机变量的关系. 2、函数关系是一种因果关系,具有确定性;而相关关系不一定是因果关系,也可能是伴随关系,是一种非确定的关系。 3、现实生活中存在着大量的相关关系。
如:人的身高与年龄;
产品的成本与生产数量;
商品的销售额与广告费;
家庭的支出与收入。等等 4、回归分析实质:通俗地讲,回归分析是寻找
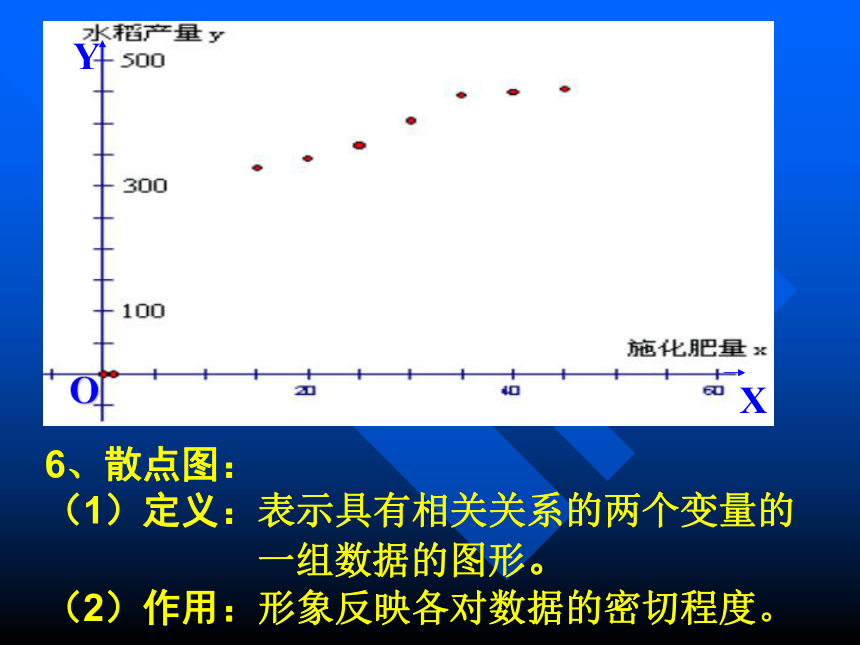
相关关系中非确定性关系的某种确定性。定义:对具有相关关系的两个变量进行统计分析的方法。例1:在7块并排、形状大小相同的试验田上进行施化肥量对水稻产量影响的试验,得到如下表所示的一组数据(单位:kg) :5、典型范例:第一次不点6、散点图:
(1)定义:表示具有相关关系的两个变量的
一组数据的图形。
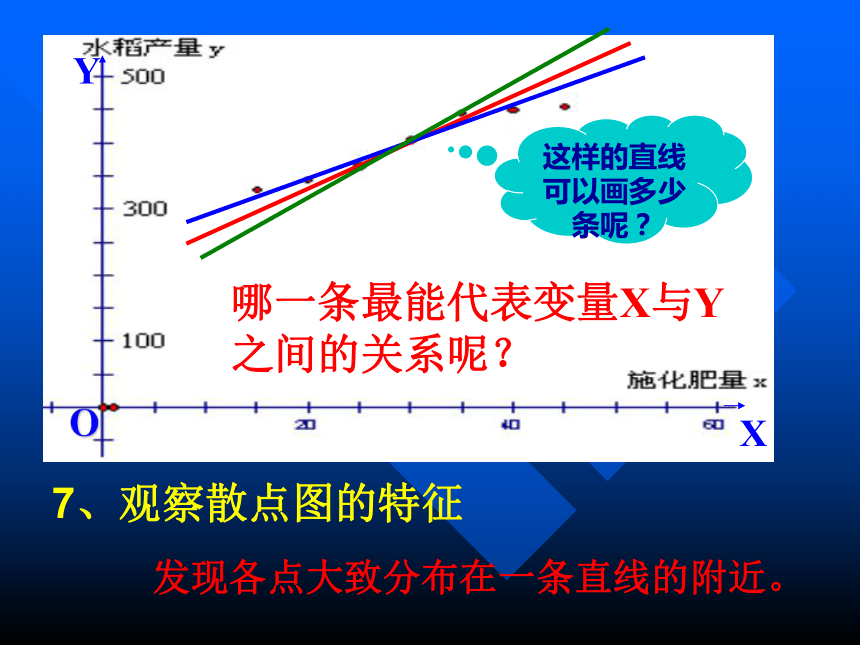
(2)作用:形象反映各对数据的密切程度。7、观察散点图的特征 发现各点大致分布在一条直线的附近。 哪一条最能代表变量X与Y之间的关系呢?这样的直线可以画多少条呢? 8、一般地,设x与y是具有相关关系的两个变量,且相应于n个观测值的n个点大致分布在一条直线的附近,我们来求在整体上与这n个点最接近的一条直线。(1)设所求的直线的方程是:
其中 是待确定的参数,于是,当变量x 取一组数值 时,相应地(2)各个偏差:的符号有正有负,相加会相互抵消。的和不能代表n个点与相应直线在整体上的接近程度。用Q来表示n个点与相应直线在整体上的接近程度。即:(3)各偏差的平方和:(4)求出使Q为最小值时的a、b的值:其中解:由题意,列出如下所示表格。因此所求回归直线方程是:由上表所可知:(5)回归直线方程的用途:
可以利用它求出相应于x的估计值。
例如:当x=28kg时,y的估计值是多少呢?例2:(2004年杭州市测验题),
右表是某省20个县城2003年的一份统计资料。其中xi表示第i个县城在2003年建成的新住宅面积(千平方米),yi表示第i个县城在2003年的家具销售量(万元)。
如果y与x之间具有线性相关关系,
求回归直线方程。解:由已知数据可以算出:即为所求的回归直线方程。9、如下图是一组观测值的散点图:按照上述方法,同样可以就这组数据求得一个回归直线方程,这显然毫无意义。任给出一组数据能否由此求出它的线形回归方程?想一想? 所求得的回归直线方程,在什么情况下才能对相应的一组数据观测值具有代表意义呢?10、相关检验:(1)样本相关系数(相关系数)(2)相关系数的范围: |r|≤ 1(3)相关系数的作用:衡量两变量之 间的线形相关程度。若|r|越接近于1,相关程度越大;
若|r|越接近于0,相关程度越小。例3、利用r的计算公式来计算例1中水稻产量与施化肥的相关系数。解:由得到相关系数(4)显著性检验的一般步骤:①、在附表3中查出与显著性水平0.05与自由度n-2(n为观测值组数)相应的相关系数临界值 .(显著性水平0.05是一个作为发生小概率事件的临界值,0.9,0.99以及上一节中用到的0.997等也都是常用的显著性水平。)设待检验的统计假设是两个变量不具有相关关系。②、根据公式求出相关系数r的值。 ③ 、检验所得结果。
如果|r|≤ ,那么可以认为y与x之间的线形关系不显著,从而接受统计假设。
如果|r|> ,表明一个发生的概率不到5%的事件在一次试验中竟发生了。这个小概率事件的发生使我们有理由认为y与x之间不具有线形相关关系的假设是不成立的,从而拒绝这一统计假设,也就是表明可以认为y与x之间具有线形相关关系。例4、按照上面的步骤,我们来检验例1中水稻产量与施化肥量之间是否存在线性相关关系。第1步:在附表3中查出与显著性水平0.05和自由度7-2相应的相关关系数临界值 。第2步:刚刚我们已经算出第3步:因为 ,这说明水稻产量与施化肥量之间存在着线性相关关系。从此也可以表明,前面我们求得的这两个变量之间的回归直线方程是有效、有意义的。课时小结:1、本节课我们学习了线形回归的几个基本概念:两个变量之间的相关关系,回归分析,散点图,回归直线方程,回归直线,线性回归分析;2、共同探讨了已知各对数据如何求回归直线方程。其推导方法是利用配方法;3、另外通过本节课的学习,我们看到,由部分观测值得到的回归直线,可以对两个变量间的线形相关关系进行估计;4、函数关系是一种理想的关系模型,而相关关系是一种更一般的情况。5、通常,在尚未确定两个变量之间是否具有线性相关关系的情况下,应先进行相关性检验,在确认其具有线性相关关系后,再求其回归直线方程。
体重预测值(cm)
=0.72kg/cm×身高 - 58.5kg.一、课题引入1、两个变量之间的关系:函数关系 非确定关系 自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系. 二、新课讲解:2、相关关系与函数关系的异同点: (一)相同点:均是指两个变量的关系。 (二)不同点:
1、函数关系是自变量与因变量之间 的关系,这种关系是两个非随机变量的关系;而相关关系是非随机变量与随机变量的关系. 2、函数关系是一种因果关系,具有确定性;而相关关系不一定是因果关系,也可能是伴随关系,是一种非确定的关系。 3、现实生活中存在着大量的相关关系。
如:人的身高与年龄;
产品的成本与生产数量;
商品的销售额与广告费;
家庭的支出与收入。等等 4、回归分析实质:通俗地讲,回归分析是寻找
相关关系中非确定性关系的某种确定性。定义:对具有相关关系的两个变量进行统计分析的方法。例1:在7块并排、形状大小相同的试验田上进行施化肥量对水稻产量影响的试验,得到如下表所示的一组数据(单位:kg) :5、典型范例:第一次不点6、散点图:
(1)定义:表示具有相关关系的两个变量的
一组数据的图形。
(2)作用:形象反映各对数据的密切程度。7、观察散点图的特征 发现各点大致分布在一条直线的附近。 哪一条最能代表变量X与Y之间的关系呢?这样的直线可以画多少条呢? 8、一般地,设x与y是具有相关关系的两个变量,且相应于n个观测值的n个点大致分布在一条直线的附近,我们来求在整体上与这n个点最接近的一条直线。(1)设所求的直线的方程是:
其中 是待确定的参数,于是,当变量x 取一组数值 时,相应地(2)各个偏差:的符号有正有负,相加会相互抵消。的和不能代表n个点与相应直线在整体上的接近程度。用Q来表示n个点与相应直线在整体上的接近程度。即:(3)各偏差的平方和:(4)求出使Q为最小值时的a、b的值:其中解:由题意,列出如下所示表格。因此所求回归直线方程是:由上表所可知:(5)回归直线方程的用途:
可以利用它求出相应于x的估计值。
例如:当x=28kg时,y的估计值是多少呢?例2:(2004年杭州市测验题),
右表是某省20个县城2003年的一份统计资料。其中xi表示第i个县城在2003年建成的新住宅面积(千平方米),yi表示第i个县城在2003年的家具销售量(万元)。
如果y与x之间具有线性相关关系,
求回归直线方程。解:由已知数据可以算出:即为所求的回归直线方程。9、如下图是一组观测值的散点图:按照上述方法,同样可以就这组数据求得一个回归直线方程,这显然毫无意义。任给出一组数据能否由此求出它的线形回归方程?想一想? 所求得的回归直线方程,在什么情况下才能对相应的一组数据观测值具有代表意义呢?10、相关检验:(1)样本相关系数(相关系数)(2)相关系数的范围: |r|≤ 1(3)相关系数的作用:衡量两变量之 间的线形相关程度。若|r|越接近于1,相关程度越大;
若|r|越接近于0,相关程度越小。例3、利用r的计算公式来计算例1中水稻产量与施化肥的相关系数。解:由得到相关系数(4)显著性检验的一般步骤:①、在附表3中查出与显著性水平0.05与自由度n-2(n为观测值组数)相应的相关系数临界值 .(显著性水平0.05是一个作为发生小概率事件的临界值,0.9,0.99以及上一节中用到的0.997等也都是常用的显著性水平。)设待检验的统计假设是两个变量不具有相关关系。②、根据公式求出相关系数r的值。 ③ 、检验所得结果。
如果|r|≤ ,那么可以认为y与x之间的线形关系不显著,从而接受统计假设。
如果|r|> ,表明一个发生的概率不到5%的事件在一次试验中竟发生了。这个小概率事件的发生使我们有理由认为y与x之间不具有线形相关关系的假设是不成立的,从而拒绝这一统计假设,也就是表明可以认为y与x之间具有线形相关关系。例4、按照上面的步骤,我们来检验例1中水稻产量与施化肥量之间是否存在线性相关关系。第1步:在附表3中查出与显著性水平0.05和自由度7-2相应的相关关系数临界值 。第2步:刚刚我们已经算出第3步:因为 ,这说明水稻产量与施化肥量之间存在着线性相关关系。从此也可以表明,前面我们求得的这两个变量之间的回归直线方程是有效、有意义的。课时小结:1、本节课我们学习了线形回归的几个基本概念:两个变量之间的相关关系,回归分析,散点图,回归直线方程,回归直线,线性回归分析;2、共同探讨了已知各对数据如何求回归直线方程。其推导方法是利用配方法;3、另外通过本节课的学习,我们看到,由部分观测值得到的回归直线,可以对两个变量间的线形相关关系进行估计;4、函数关系是一种理想的关系模型,而相关关系是一种更一般的情况。5、通常,在尚未确定两个变量之间是否具有线性相关关系的情况下,应先进行相关性检验,在确认其具有线性相关关系后,再求其回归直线方程。
