3.3 垂径定理 课件(共31张PPT)
文档属性
| 名称 | 3.3 垂径定理 课件(共31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-10 10:51:36 | ||
图片预览






文档简介
(共31张PPT)
3.3 垂径定理
北师大版 九年级 下册
教学目标
教学目标:1、运用探索、推理,理解垂直于弦的直径的性质和推论,并
能应用它解决一些简单的计算、证明和作图问题;
2、拓展思维,与实践相结合,熟练运用圆的垂径定理,学会
运用垂径定理解决相关的实际问题;
3、通过手脑结合,掌握圆的对称性,并学会证明垂径定理和
其推论.
教学重点:理解垂直于弦的直径的性质和推论,并能应用它解决一些简单的
计算、证明和作图问题.
教学难点:熟练运用圆的垂径定理,学会运用垂径定理解决相关的实际问题.
新知讲解
情境引入
1400多年前,我国隋朝建造的赵州石拱桥(如图)的桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4m,拱高(弧的中点到弦的距离,也叫弓形高)为7.2m,求桥拱的半径(精确到0.1m).
7.23m
37m
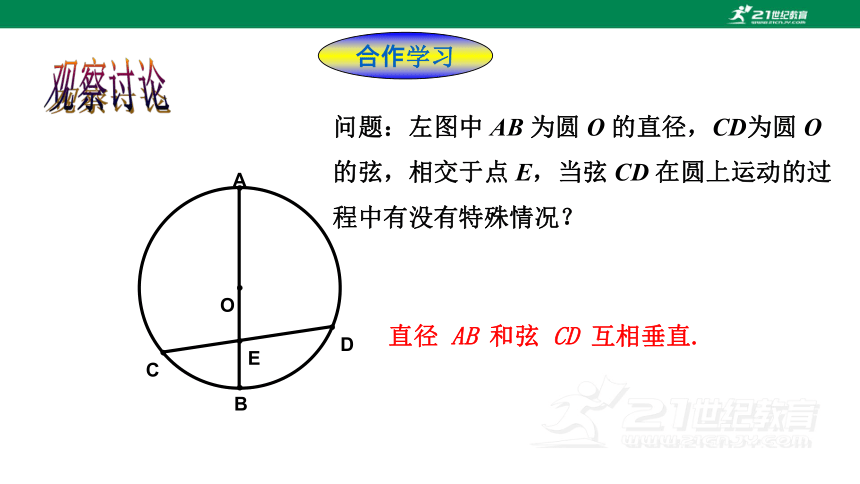
问题:左图中 AB 为圆 O 的直径,CD为圆 O 的弦,相交于点 E,当弦 CD 在圆上运动的过程中有没有特殊情况?
直径 AB 和弦 CD 互相垂直.
观察讨论
合作学习
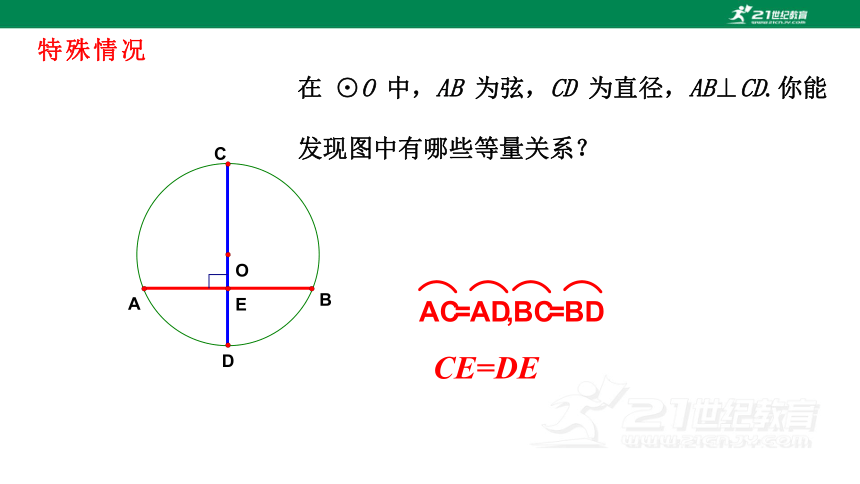
特殊情况
在 ⊙O 中,AB 为弦,CD 为直径,AB⊥CD.你能发现图中有哪些等量关系?
CE=DE
证明结论
已知:在 ⊙O 中,CD 是直径,AB 是弦,CD⊥AB,垂足为 E.
求证:AE=BE,AC=BC,AD=BD.
⌒
⌒
⌒
⌒
C
.
O
A
E
B
D
新知讲解
证明:连接 OA,OB,则 OA = OB.
在 Rt△OAE 和 Rt△OBE 中,
∵ OA = OB,OE = OE, ∴ Rt△OAE ≌ Rt△OBE.
∴ AE = BE. ∴ 点 A 和点 B 关于 CD 对称.
∵ ⊙O 关于直径 CD 对称,
∴ 当圆沿着直径 CD 对折时,
点 A 与点 B 重合, 重合,
⌒ ⌒
AC与BC
⌒ ⌒
AD与BD重合.
⌒ ⌒
∴AC=BC,
⌒ ⌒
AD=BD.
C
.
O
A
E
B
D
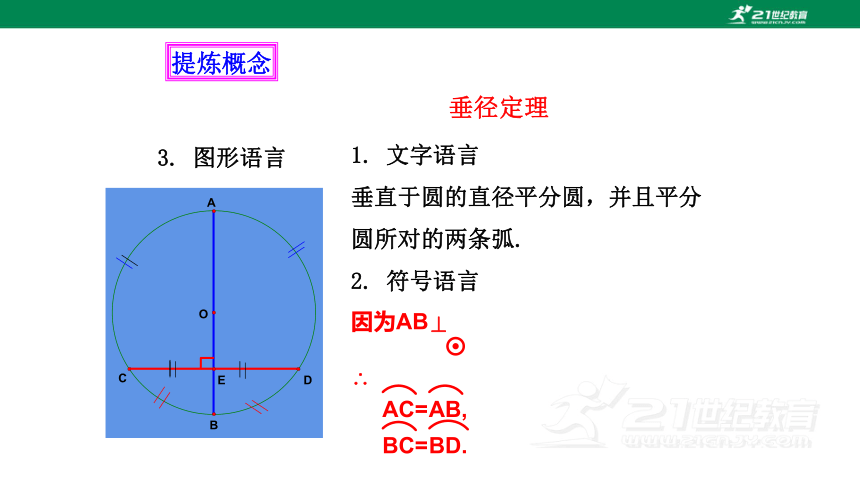
提炼概念
垂径定理
1. 文字语言
垂直于圆的直径平分圆,并且平分 圆所对的两条弧.
2. 符号语言
3. 图形语言
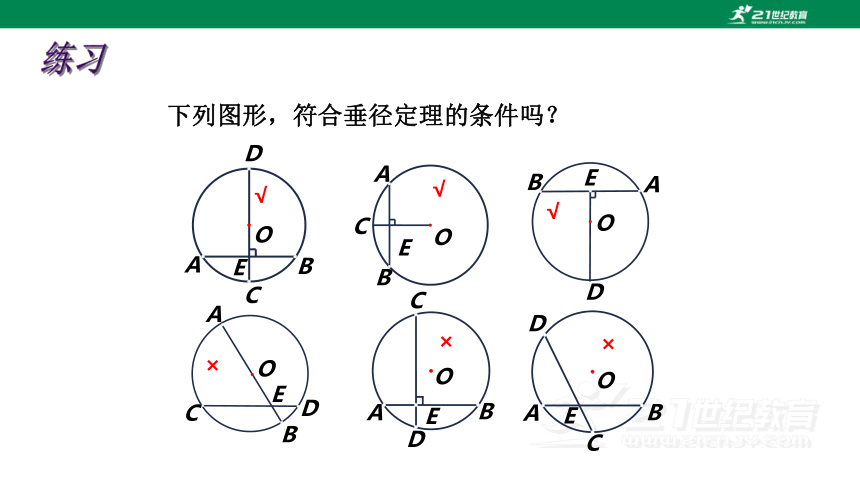
练习
下列图形,符合垂径定理的条件吗?
E
O
A
B
D
C
O
B
A
E
D
E
O
C
D
A
B
E
A
B
C
D
O
E
A
B
D
C
O
E
O
A
B
C
×
×
×
√
√
√
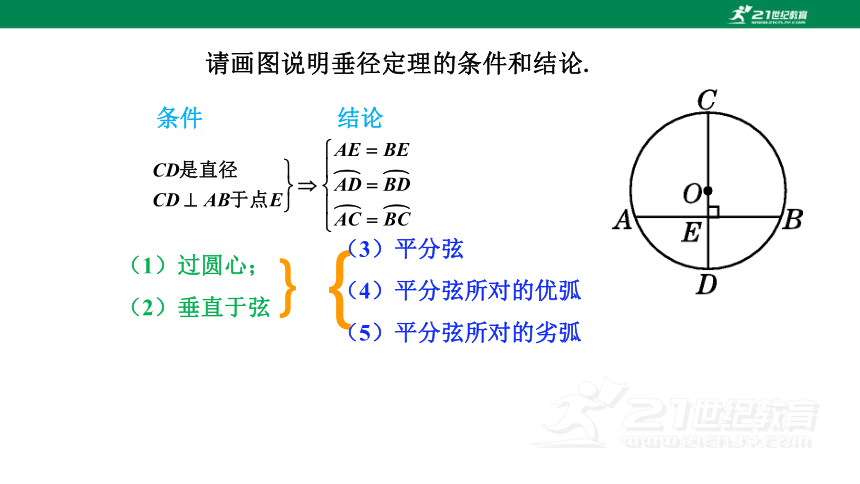
条件
结论
(1)过圆心;
(2)垂直于弦
}
{
(3)平分弦
(4)平分弦所对的优弧
(5)平分弦所对的劣弧
请画图说明垂径定理的条件和结论.
如果把垂径定理(垂直于弦的直径平分弦,并且平分弦所对的两条弧)结论与题设交换一条,命题是真命题吗?
①过圆心 ;②垂直于弦; ③平分弦;
④平分弦所对的优弧 ; ⑤平分弦所对的劣弧.
上述五个条件中的任何两个条件都可以推出其他三个结论吗?
思考探索
想一想
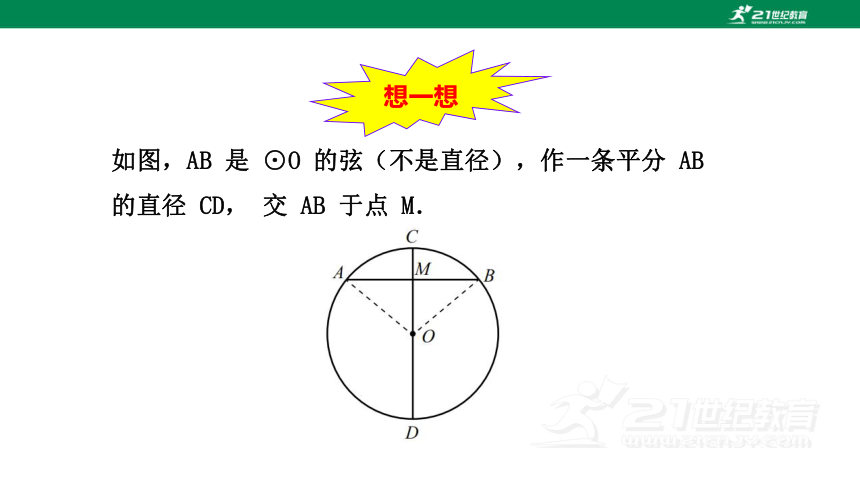
如图,AB 是 ⊙O 的弦(不是直径),作一条平分 AB 的直径 CD, 交 AB 于点 M.
(1)如图是轴对称图形吗?如果是,其对称轴是什么? (2)你能发现图中有哪些等量关系?说一说你的理由.
(1)是轴对称图形,对称轴是CD所在的直线.
(2)AM=BM,
⌒ ⌒
AD=BD.
⌒ ⌒
AC=BC,
思考:“不是直径”这个条件能去掉吗?如果不能,请举出反例.
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.
垂径定理的推论
·
O
A
B
C
D
特别说明:
圆的两条直径是互相平分的.
归纳总结
垂径定理的本质是:
知二得三
(1)一条直线过圆心
(2)这条直线垂直于弦
(3)这条直线平分不是直径的弦
(4)这条直线平分不是直径的弦所对的优弧
(5)这条直线平分不是直径的弦所对的劣弧
典例精讲
例:如图, —条公路的转弯处是一段圆弧(即图中 ,点O 是 所在圆的圆心),其中CD= 600m, E 为 上一点,且OE丄CD,垂足为F,EF =90m.求这段弯路的半径.
连接OC.设弯路的半径为R m,则OF= (R-90) m.
∵OE ⊥CD,∴ CF = CD = ×600 = 300 (m).
在Rt△OCF 中 ,根据勾股定理,得OC 2=CF 2+OF 2,
即R 2 = 3002 + (R-90)2.
解这个方程,得R=545.
所以,这段弯路的半径为545 m.
解:
归纳概念
在圆中有关弦长a,半径r, 弦心距d(圆心到弦的距离),弓形高h的计算题,常常通过连半径或作弦心距构造直角三角形,利用垂径定理和勾股定理求解.
涉及垂径定理时辅助线的添加方法
弦a,弦心距d,弓形高h,半径r之间有以下关系:
弓形中重要数量关系
A
B
C
D
O
h
r
d
d+h=r
O
A
B
C
·
课堂练习
1.如图,已知⊙O 的直径AB⊥CD 于点E,则下列结论中错误的是( )
A.CE=DE
B.AE=OE
C.
D.△OCE ≌ △ODE
B
2.如图,在半径为5的⊙O 中,弦AB=6,OP⊥AB,垂足为点P,则OP 的长为( )
A.3
B.2.5
C.4
D.3.5
C
3. 已知☉O的半径为10cm,弦MN∥EF,且MN=12cm,EF=16cm,则弦MN和EF之间的距离为 .
4.如图,⊙O的直径为10,弦AB=8,P为AB上的一个动点,那么OP长的取值范围 .
14cm或2cm
3cm≤OP≤5cm
5.某市某居民区一处地下圆形管道破裂,修理人员准备更换一段新管道,如图①,污水面宽度为60 cm,水面至管道顶部的距离为10 cm,问修理人员应准备内径为多大的管道?
解:如图②,弦AB 表示污水水面,点O 为圆心,圆形管道的内
径即为⊙O 的直径.设半径为r cm,过点O 作OC⊥AB 于点D,
与 交于点C,根据垂径定理知,点D 是AB 的中点,点
C 是 的中点,CD 就是污水水面至管道顶部的距离.由
题意可知:AB=60 cm,CD=10 cm,∴BD= AB=30
cm,OD=(r-10) cm. 在Rt△DOB 中,BD 2+OD 2=OB 2,即
302+(r-10)2=r 2,解得r=50.∴2r=2×50=100(cm).
答:修理人员应准备内径为100 cm的管道.
6.已知在以点O 为圆心的两个同心圆中,大圆的弦AB 交小圆于点C,D (如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆心O 到直线AB 的距离为6,求AC 的长.
如图,过点O 作OE⊥AB 于点E,
则CE=DE,AE=BE.
∴AE-CE=BE-DE,即AC=BD.
如图,连接OA,OC,由(1)可知,
OE⊥AB 且OE⊥CD,
∵圆心O 到直线AB 的距离为6,∴OE=6.
∴CE=
AE=
∴AC=AE-CE=8-2
(1)证明:
(2)解:
7. 1400年前,我国隋朝建造的赵州石拱桥(如图)是圆弧形,它的跨度(即弧所 对的弦长)为37.4 m,拱高(即弧的中点到弦的距离)为7.2 m,求桥拱所在圆的半径(结果精确到0.1).
解:如图,∵OD⊥AB,
∴AD= AB= ×37.4=18.7(m).
在Rt△ODA 中,
OD=(R-7.2) m,OA=R m,
∴R 2=(R-7.2)2+18.72,
解得R≈27.9.
∴桥拱所在圆的半径约为27.9 m.
课堂总结
垂径定理
内容
推论
辅助线
一条直线满足:①过圆心;②垂直于弦; ③平分弦(不是直径); ④平分弦所对的优弧;⑤平分弦所对的劣弧.满足其中两个条件就可以推出其它三个结论(“知二推三”)
垂直于弦的直径平分这条弦,
并且平分弦所对的弧.
两条辅助线:
连半径,作弦心距
构造Rt△利用勾股定理计算或建立方程.
基本图形及变式图形
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
3.3 垂径定理
北师大版 九年级 下册
教学目标
教学目标:1、运用探索、推理,理解垂直于弦的直径的性质和推论,并
能应用它解决一些简单的计算、证明和作图问题;
2、拓展思维,与实践相结合,熟练运用圆的垂径定理,学会
运用垂径定理解决相关的实际问题;
3、通过手脑结合,掌握圆的对称性,并学会证明垂径定理和
其推论.
教学重点:理解垂直于弦的直径的性质和推论,并能应用它解决一些简单的
计算、证明和作图问题.
教学难点:熟练运用圆的垂径定理,学会运用垂径定理解决相关的实际问题.
新知讲解
情境引入
1400多年前,我国隋朝建造的赵州石拱桥(如图)的桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4m,拱高(弧的中点到弦的距离,也叫弓形高)为7.2m,求桥拱的半径(精确到0.1m).
7.23m
37m
问题:左图中 AB 为圆 O 的直径,CD为圆 O 的弦,相交于点 E,当弦 CD 在圆上运动的过程中有没有特殊情况?
直径 AB 和弦 CD 互相垂直.
观察讨论
合作学习
特殊情况
在 ⊙O 中,AB 为弦,CD 为直径,AB⊥CD.你能发现图中有哪些等量关系?
CE=DE
证明结论
已知:在 ⊙O 中,CD 是直径,AB 是弦,CD⊥AB,垂足为 E.
求证:AE=BE,AC=BC,AD=BD.
⌒
⌒
⌒
⌒
C
.
O
A
E
B
D
新知讲解
证明:连接 OA,OB,则 OA = OB.
在 Rt△OAE 和 Rt△OBE 中,
∵ OA = OB,OE = OE, ∴ Rt△OAE ≌ Rt△OBE.
∴ AE = BE. ∴ 点 A 和点 B 关于 CD 对称.
∵ ⊙O 关于直径 CD 对称,
∴ 当圆沿着直径 CD 对折时,
点 A 与点 B 重合, 重合,
⌒ ⌒
AC与BC
⌒ ⌒
AD与BD重合.
⌒ ⌒
∴AC=BC,
⌒ ⌒
AD=BD.
C
.
O
A
E
B
D
提炼概念
垂径定理
1. 文字语言
垂直于圆的直径平分圆,并且平分 圆所对的两条弧.
2. 符号语言
3. 图形语言
练习
下列图形,符合垂径定理的条件吗?
E
O
A
B
D
C
O
B
A
E
D
E
O
C
D
A
B
E
A
B
C
D
O
E
A
B
D
C
O
E
O
A
B
C
×
×
×
√
√
√
条件
结论
(1)过圆心;
(2)垂直于弦
}
{
(3)平分弦
(4)平分弦所对的优弧
(5)平分弦所对的劣弧
请画图说明垂径定理的条件和结论.
如果把垂径定理(垂直于弦的直径平分弦,并且平分弦所对的两条弧)结论与题设交换一条,命题是真命题吗?
①过圆心 ;②垂直于弦; ③平分弦;
④平分弦所对的优弧 ; ⑤平分弦所对的劣弧.
上述五个条件中的任何两个条件都可以推出其他三个结论吗?
思考探索
想一想
如图,AB 是 ⊙O 的弦(不是直径),作一条平分 AB 的直径 CD, 交 AB 于点 M.
(1)如图是轴对称图形吗?如果是,其对称轴是什么? (2)你能发现图中有哪些等量关系?说一说你的理由.
(1)是轴对称图形,对称轴是CD所在的直线.
(2)AM=BM,
⌒ ⌒
AD=BD.
⌒ ⌒
AC=BC,
思考:“不是直径”这个条件能去掉吗?如果不能,请举出反例.
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.
垂径定理的推论
·
O
A
B
C
D
特别说明:
圆的两条直径是互相平分的.
归纳总结
垂径定理的本质是:
知二得三
(1)一条直线过圆心
(2)这条直线垂直于弦
(3)这条直线平分不是直径的弦
(4)这条直线平分不是直径的弦所对的优弧
(5)这条直线平分不是直径的弦所对的劣弧
典例精讲
例:如图, —条公路的转弯处是一段圆弧(即图中 ,点O 是 所在圆的圆心),其中CD= 600m, E 为 上一点,且OE丄CD,垂足为F,EF =90m.求这段弯路的半径.
连接OC.设弯路的半径为R m,则OF= (R-90) m.
∵OE ⊥CD,∴ CF = CD = ×600 = 300 (m).
在Rt△OCF 中 ,根据勾股定理,得OC 2=CF 2+OF 2,
即R 2 = 3002 + (R-90)2.
解这个方程,得R=545.
所以,这段弯路的半径为545 m.
解:
归纳概念
在圆中有关弦长a,半径r, 弦心距d(圆心到弦的距离),弓形高h的计算题,常常通过连半径或作弦心距构造直角三角形,利用垂径定理和勾股定理求解.
涉及垂径定理时辅助线的添加方法
弦a,弦心距d,弓形高h,半径r之间有以下关系:
弓形中重要数量关系
A
B
C
D
O
h
r
d
d+h=r
O
A
B
C
·
课堂练习
1.如图,已知⊙O 的直径AB⊥CD 于点E,则下列结论中错误的是( )
A.CE=DE
B.AE=OE
C.
D.△OCE ≌ △ODE
B
2.如图,在半径为5的⊙O 中,弦AB=6,OP⊥AB,垂足为点P,则OP 的长为( )
A.3
B.2.5
C.4
D.3.5
C
3. 已知☉O的半径为10cm,弦MN∥EF,且MN=12cm,EF=16cm,则弦MN和EF之间的距离为 .
4.如图,⊙O的直径为10,弦AB=8,P为AB上的一个动点,那么OP长的取值范围 .
14cm或2cm
3cm≤OP≤5cm
5.某市某居民区一处地下圆形管道破裂,修理人员准备更换一段新管道,如图①,污水面宽度为60 cm,水面至管道顶部的距离为10 cm,问修理人员应准备内径为多大的管道?
解:如图②,弦AB 表示污水水面,点O 为圆心,圆形管道的内
径即为⊙O 的直径.设半径为r cm,过点O 作OC⊥AB 于点D,
与 交于点C,根据垂径定理知,点D 是AB 的中点,点
C 是 的中点,CD 就是污水水面至管道顶部的距离.由
题意可知:AB=60 cm,CD=10 cm,∴BD= AB=30
cm,OD=(r-10) cm. 在Rt△DOB 中,BD 2+OD 2=OB 2,即
302+(r-10)2=r 2,解得r=50.∴2r=2×50=100(cm).
答:修理人员应准备内径为100 cm的管道.
6.已知在以点O 为圆心的两个同心圆中,大圆的弦AB 交小圆于点C,D (如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆心O 到直线AB 的距离为6,求AC 的长.
如图,过点O 作OE⊥AB 于点E,
则CE=DE,AE=BE.
∴AE-CE=BE-DE,即AC=BD.
如图,连接OA,OC,由(1)可知,
OE⊥AB 且OE⊥CD,
∵圆心O 到直线AB 的距离为6,∴OE=6.
∴CE=
AE=
∴AC=AE-CE=8-2
(1)证明:
(2)解:
7. 1400年前,我国隋朝建造的赵州石拱桥(如图)是圆弧形,它的跨度(即弧所 对的弦长)为37.4 m,拱高(即弧的中点到弦的距离)为7.2 m,求桥拱所在圆的半径(结果精确到0.1).
解:如图,∵OD⊥AB,
∴AD= AB= ×37.4=18.7(m).
在Rt△ODA 中,
OD=(R-7.2) m,OA=R m,
∴R 2=(R-7.2)2+18.72,
解得R≈27.9.
∴桥拱所在圆的半径约为27.9 m.
课堂总结
垂径定理
内容
推论
辅助线
一条直线满足:①过圆心;②垂直于弦; ③平分弦(不是直径); ④平分弦所对的优弧;⑤平分弦所对的劣弧.满足其中两个条件就可以推出其它三个结论(“知二推三”)
垂直于弦的直径平分这条弦,
并且平分弦所对的弧.
两条辅助线:
连半径,作弦心距
构造Rt△利用勾股定理计算或建立方程.
基本图形及变式图形
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
