【班海精品】人教版(新)八下-16.2 二次根式的乘除 第二课时【优质课件】
文档属性
| 名称 | 【班海精品】人教版(新)八下-16.2 二次根式的乘除 第二课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-10 09:07:45 | ||
图片预览







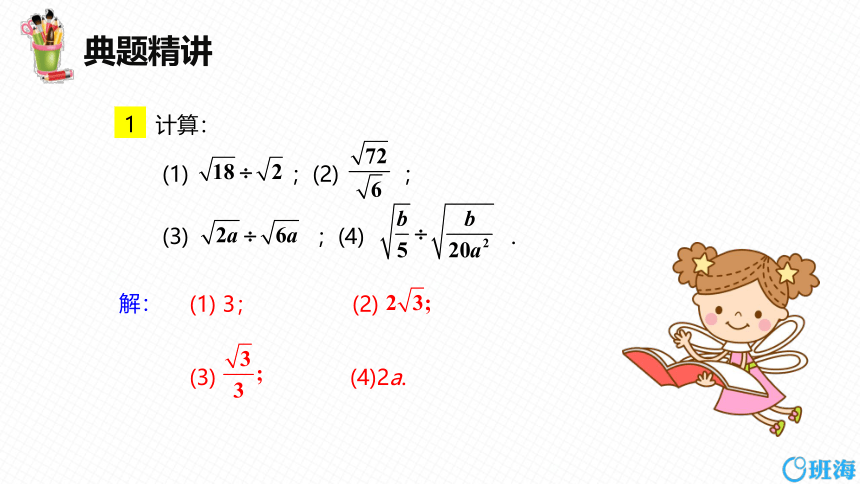


文档简介
(共39张PPT)
16.2 二次根式的乘除
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
二次根式的乘法法则是什么内容?
化简二次根式的一般步骤是什么?
新课精讲
探索新知
1
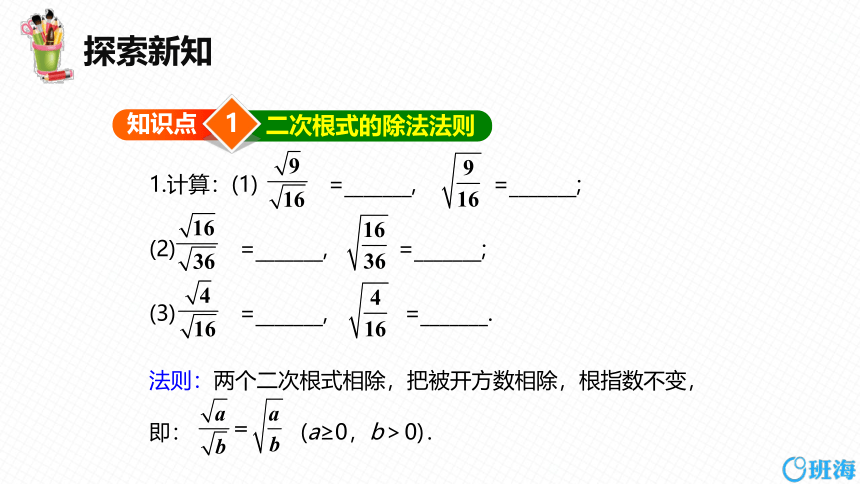
知识点
二次根式的除法法则
1.计算:(1) =_______, =_______;
(2) =_______, =_______;
(3) =_______, =_______.
法则:两个二次根式相除,把被开方数相除,根指数不变,即: (a≥0,b>0).
探索新知
解:(1)
(2)
例1 计算:
(1) ;(2)
探索新知
总 结
利用二次根式的除法法则进行计算,被开方数相除时,可以用“除以一个不为零的数等于乘这个数的倒数”进行约分、化简.
典题精讲
1 计算:
(1) ;(2) ;
(3) ;(4) .
(1) 3; (2)
(3) (4)2a.
解:
典题精讲
2 成立的条件是( )
A.a≠1 B.a≥1且a≠3
C.a>1 D.a≥3
3 计算 的结果是( )
A. B. C. D.
D
C
典题精讲
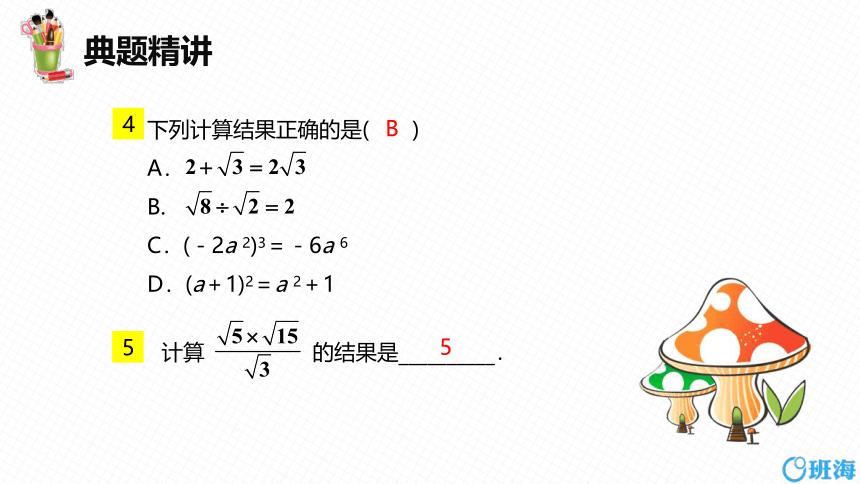
下列计算结果正确的是( )
A.
B.
C.(-2a 2)3=-6a 6
D.(a+1)2=a 2+1
4
B
计算 的结果是__________.
5
5
探索新知
2
知识点
商的算术平方根的性质
把 反过来,就得到 (a≥0,
b>0) ,利用它可以进行二次根式的化简.
探索新知
例2 化简:(1) (2)
解:(1)
(2)
探索新知
例3 计算:(1) (2) (3)
解:(1)解法1:
解法2:
(2)
(3)
探索新知
总 结
分母有理化一般经历如下三步:
“一移”,即将分子、分母中能开得尽方的因数(式)移
到根号外;
“二乘”,即将分子、分母同乘分母的有理化因数(式);
“三化”,即化简计算.
典题精讲
1 下列各式计算正确的是( )
A. B.
C. D.
2 若 ,则a 的取值范围是( )
A.a≤0 B.a<0 C.a>0 D.0C
D
典题精讲
下列等式不一定成立的是( )
A. =(b≠0)
B.a 3·a-5= (a≠0)
C.a 2-4b 2=(a+2b)(a-2b)
D.(-2a 3) 2=4a 6
3
A
下列计算正确的是( )
B.
C. D.
4
A
探索新知
3
知识点
最简二次根式
定义:如果一个二次根式满足以下两个条件,
那么这个二次根式叫做最简二次根式:
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
探索新知
归 纳
最简二次根式必须满足:
(1)被开方数不含分母,也就是被开方数必须是整数(式);
(2)被开方数中每个因数(式)的指数都小于根指数2,即每个因数(式)的指数都是1.
探索新知
例4 下列各式中,哪些是最简二次根式?哪些不是最简
二次根式?不是最简二次根式的,请说明理由.
(1) (2) (3) (4)
(5) (6)
导引:根据最简二次根式的定义进行判断.
解:(1)不是最简二次根式,因为被开方数中含有分母.
(2)是最简二次根式.
(3)不是最简二次根式,因为被开方数是小数(即含有分母).
探索新知
(4)不是最简二次根式,因为被开方数24x中含有能开得尽方的因数4,4=22.
(5)不是最简二次根式,因为x 3+6x 2+9x=x (x 2+6x+9)=x (x+3)2,被开方数中含有能开得尽方的因式.
(6)不是最简二次根式,因为分母中有二次根式.综上,只有(2)是最简二次根式.
探索新知
例5 设长方形的面积为S,相邻两边长分别为a,b.
已知S = ,b= ,求 a.
解:因为S=ab,所以
典题精讲
1 把下列二次根式化成最简二次根式:
(1) (2) (3) (4)
(1) ; (2) ;
(3) (4)
解:
典题精讲
2 设长方形的面积为S,相邻两边长分别为a,b.
已知S=16,b= ,求a.
解:由题意得S=ab,所以
下列根式是最简二次根式的是( )
A. B.
C. D.
3
C
易错提醒
计算:
正解:
原式=
易错提醒
易错点:在计算过程中由于弄错运算顺序导致错误.
错解:
与 互为倒数,在计算时容易感觉后两个式子方便计算,就先计算后面的乘法运算,从而得出错误答案2 .
诊断:
学以致用
小明的作业本上有以下四题:① =4a2;
② ;③ ;
④ . 做错的题是( )
A.① B.② C.③ D.④
1
D
计算 的值为( )
A. B.
C. D.
2
C
小试牛刀
设 =a, =b,用含a,b 的式子表示 ,则下列表示正确的是( )
A.0.3ab B.3ab
C.0.1ab 2 D.0.1a 2b
3
A
小试牛刀
小试牛刀
下列二次根式中属于最简二次根式的是( )
A. B.
C. D.
4
D
已知xy<0,化简二次根式 的正确结果为( )
A. B.
C. D.
5
B
小试牛刀
6 计算:
(1) 原式=
解:
(2) 原式=
小试牛刀
7 已知 ,且x 为奇数,求(1+x ) 的值.
解:
∵ ,∴ ∴6≤x<9.
又∵x 是奇数,∴x=7.
∴(1+x ) =(1+x ) =
(1+x ) 当x=7时,原式=
小试牛刀
8 老师在讲解“二次根式及其性质”时,在黑板上写下了下面的一题作为练习:已知 =a, =b,用含有a,b 的代数式表示 .
甲的解法:
乙的解法: ,
因为 ,所以
请你解答下面的问题:
(1)甲、乙两人的解法都正确吗?
(2)请你再给出一种不同于上面两人的解法.
小试牛刀
都正确.
(2)
解:
小试牛刀
9 化简 ,甲、乙两位同学的解法如下:
甲:
乙:
以上两种化简的步骤叫做分母有理化.
仿照上述两种方法化简: .
小试牛刀
方法1:
解:
方法2:
课堂小结
课堂小结
1.二次根式的除法:
两个二次根式相除,把被开方数相除,根指数不变,即:
(a≥0,b>0).
2.最简二次根式:
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
16.2 二次根式的乘除
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
二次根式的乘法法则是什么内容?
化简二次根式的一般步骤是什么?
新课精讲
探索新知
1
知识点
二次根式的除法法则
1.计算:(1) =_______, =_______;
(2) =_______, =_______;
(3) =_______, =_______.
法则:两个二次根式相除,把被开方数相除,根指数不变,即: (a≥0,b>0).
探索新知
解:(1)
(2)
例1 计算:
(1) ;(2)
探索新知
总 结
利用二次根式的除法法则进行计算,被开方数相除时,可以用“除以一个不为零的数等于乘这个数的倒数”进行约分、化简.
典题精讲
1 计算:
(1) ;(2) ;
(3) ;(4) .
(1) 3; (2)
(3) (4)2a.
解:
典题精讲
2 成立的条件是( )
A.a≠1 B.a≥1且a≠3
C.a>1 D.a≥3
3 计算 的结果是( )
A. B. C. D.
D
C
典题精讲
下列计算结果正确的是( )
A.
B.
C.(-2a 2)3=-6a 6
D.(a+1)2=a 2+1
4
B
计算 的结果是__________.
5
5
探索新知
2
知识点
商的算术平方根的性质
把 反过来,就得到 (a≥0,
b>0) ,利用它可以进行二次根式的化简.
探索新知
例2 化简:(1) (2)
解:(1)
(2)
探索新知
例3 计算:(1) (2) (3)
解:(1)解法1:
解法2:
(2)
(3)
探索新知
总 结
分母有理化一般经历如下三步:
“一移”,即将分子、分母中能开得尽方的因数(式)移
到根号外;
“二乘”,即将分子、分母同乘分母的有理化因数(式);
“三化”,即化简计算.
典题精讲
1 下列各式计算正确的是( )
A. B.
C. D.
2 若 ,则a 的取值范围是( )
A.a≤0 B.a<0 C.a>0 D.0
D
典题精讲
下列等式不一定成立的是( )
A. =(b≠0)
B.a 3·a-5= (a≠0)
C.a 2-4b 2=(a+2b)(a-2b)
D.(-2a 3) 2=4a 6
3
A
下列计算正确的是( )
B.
C. D.
4
A
探索新知
3
知识点
最简二次根式
定义:如果一个二次根式满足以下两个条件,
那么这个二次根式叫做最简二次根式:
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
探索新知
归 纳
最简二次根式必须满足:
(1)被开方数不含分母,也就是被开方数必须是整数(式);
(2)被开方数中每个因数(式)的指数都小于根指数2,即每个因数(式)的指数都是1.
探索新知
例4 下列各式中,哪些是最简二次根式?哪些不是最简
二次根式?不是最简二次根式的,请说明理由.
(1) (2) (3) (4)
(5) (6)
导引:根据最简二次根式的定义进行判断.
解:(1)不是最简二次根式,因为被开方数中含有分母.
(2)是最简二次根式.
(3)不是最简二次根式,因为被开方数是小数(即含有分母).
探索新知
(4)不是最简二次根式,因为被开方数24x中含有能开得尽方的因数4,4=22.
(5)不是最简二次根式,因为x 3+6x 2+9x=x (x 2+6x+9)=x (x+3)2,被开方数中含有能开得尽方的因式.
(6)不是最简二次根式,因为分母中有二次根式.综上,只有(2)是最简二次根式.
探索新知
例5 设长方形的面积为S,相邻两边长分别为a,b.
已知S = ,b= ,求 a.
解:因为S=ab,所以
典题精讲
1 把下列二次根式化成最简二次根式:
(1) (2) (3) (4)
(1) ; (2) ;
(3) (4)
解:
典题精讲
2 设长方形的面积为S,相邻两边长分别为a,b.
已知S=16,b= ,求a.
解:由题意得S=ab,所以
下列根式是最简二次根式的是( )
A. B.
C. D.
3
C
易错提醒
计算:
正解:
原式=
易错提醒
易错点:在计算过程中由于弄错运算顺序导致错误.
错解:
与 互为倒数,在计算时容易感觉后两个式子方便计算,就先计算后面的乘法运算,从而得出错误答案2 .
诊断:
学以致用
小明的作业本上有以下四题:① =4a2;
② ;③ ;
④ . 做错的题是( )
A.① B.② C.③ D.④
1
D
计算 的值为( )
A. B.
C. D.
2
C
小试牛刀
设 =a, =b,用含a,b 的式子表示 ,则下列表示正确的是( )
A.0.3ab B.3ab
C.0.1ab 2 D.0.1a 2b
3
A
小试牛刀
小试牛刀
下列二次根式中属于最简二次根式的是( )
A. B.
C. D.
4
D
已知xy<0,化简二次根式 的正确结果为( )
A. B.
C. D.
5
B
小试牛刀
6 计算:
(1) 原式=
解:
(2) 原式=
小试牛刀
7 已知 ,且x 为奇数,求(1+x ) 的值.
解:
∵ ,∴ ∴6≤x<9.
又∵x 是奇数,∴x=7.
∴(1+x ) =(1+x ) =
(1+x ) 当x=7时,原式=
小试牛刀
8 老师在讲解“二次根式及其性质”时,在黑板上写下了下面的一题作为练习:已知 =a, =b,用含有a,b 的代数式表示 .
甲的解法:
乙的解法: ,
因为 ,所以
请你解答下面的问题:
(1)甲、乙两人的解法都正确吗?
(2)请你再给出一种不同于上面两人的解法.
小试牛刀
都正确.
(2)
解:
小试牛刀
9 化简 ,甲、乙两位同学的解法如下:
甲:
乙:
以上两种化简的步骤叫做分母有理化.
仿照上述两种方法化简: .
小试牛刀
方法1:
解:
方法2:
课堂小结
课堂小结
1.二次根式的除法:
两个二次根式相除,把被开方数相除,根指数不变,即:
(a≥0,b>0).
2.最简二次根式:
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
