【班海精品】人教版(新)八下-19.1 函数【优质教案】
文档属性
| 名称 | 【班海精品】人教版(新)八下-19.1 函数【优质教案】 |  | |
| 格式 | doc | ||
| 文件大小 | 482.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 10:20:43 | ||
图片预览




文档简介
班海数学精批——一本可精细批改的教辅
19.1 函数
变量
知识目标:理解变量与函数概念以及相互之间的关系
能力目标:增强对变量的理解
情感目标:渗透事物是运动的,运动是有规律的辩证思想
重点:变量与常量
难点:对变量的判断
引入:
信息1:当你坐在摩天轮上时,想一想,随着时间的变化,你离开地面的高度是如何变化的?
信息2:汽车以60km/h的速度匀速前进,行驶里程为skm,行驶的时间为th,先填写下面的表格,在试用含t的式子表示s.
t/m 1 2 3 4 [] 5
s/km [] []
[]
新课:
问题:(1)每张电影票的售价为10元,如果早场售出票150张,日场售出票205张,晚场售出票310张,三场电影的票房收入各多少元?设一场电影受出票x张,票房收入为y元,怎样用含x的式子表示y []
(2)在一根弹簧的下端悬挂中重物,改变并记录重物的质量,观察并记录弹簧长度的变化规律,如果弹簧原长10cm,每1kg重物使弹簧伸长0. 5cm,怎样用含重物质量 m(单位:kg)的式子表示受力后弹簧长度l(单位:cm)?
(3)要画一个面积为10cm2的圆,圆的半径应取多少?圆的面积为20cm2呢?怎样用含圆面积S的式子表示圆的半径r
(4)用10m长的绳子围成长方形,试改变长方形的长度,观察长方形的面积怎样变化。记录不同的长方形的长度值,计算相应的长方形面积的值,探索它们的变化规律,设长方形的长为xm,面积为Sm2,怎样用含x的式子表示S?
在一个变化过程中,我们称数值发生变化的量为变量(variable).数值始终不变的量为常量。
指出上述问题中的变量和常量。
范例:写出下列各问题中所满足的关系式,并指出各个关系式中,哪些量是变量,哪些量是常量?
(1) 用总长为60m的篱笆围成矩形场地,求矩形的面积S(m2)与一边长x(m)之间的关系式;
(2) 购买单价是0.4元的铅笔,总金额y(元)与购买的铅笔的数量n(支)的关系;
(3) 运动员在4000m一圈的跑道上训练,他跑一圈所用的时间t(s)与跑步的速度v(m/s)的关系;
(4) 银行规定:五年期存款的年利率为2.79%,则某人存入x元本金与所得的本息和y(元)之间的关系。[]
活动:1.分别指出下列各式中的常量与变量.
(1) 圆的面积公式S=πr2;
(2) 正方形的l=4a;
(3) 大米的单价为2.50元/千克,则购买的大米的数量x(kg)与金额与金额y的关系为y=2.5x.
2.写出下列问题的关系式,并指出不、常量和变量.[]
(1) 某种活期储蓄的月利率为0.16%,存入10000元本金,按国家规定,取款时,应缴纳利息部分的20%的利息税,求这种活期储蓄扣除利息税后实得的本息和y(元)与所存月数x之间的关系式.
(2) 如图,每个图中是由若干个盆花组成的图案,每条边(包括两个顶点)有n盆花,每个图案的花盆总数是S,求S与n之间的关系式.
思考:怎样列变量之间的关系式?
小结:变量与常量
作业:
函数
知识目标:理解函数的概念,能准确识别出函数关系中的自变量和函数
能力目标:会用变化的量描述事物
情感目标:回用运动的观点观察事物,分析事物
重点:函数的概念
难点:函数的概念
教学媒体:多媒体电脑,计算器
教学说明:注意区分函数与非函数的关系,学会确定自变量的取值范围
教学设计:
引入:
信息1:小明在14岁生日时,看到他爸爸为他记录的以前各年周岁时体重数值表,你能看出小明各周岁时体重是如何变化的吗?
周岁 1 2 3 4 5 6 7 8[] 9 10 11 12 13
体重(kg) 9.3 11.8 13.5[] 15.4 16.7 18.0 19.6 21.5 23.2[] 25 27.6 30.2 32.5
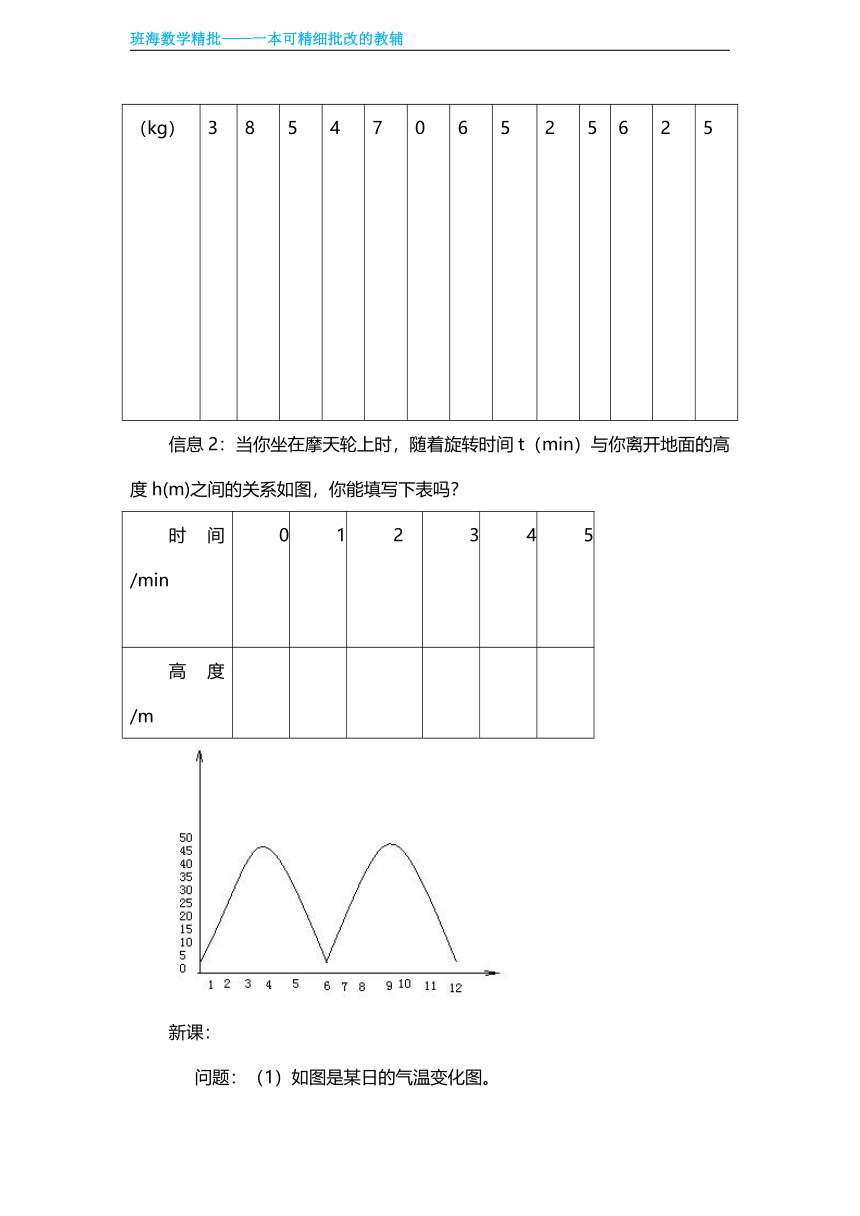
信息2:当你坐在摩天轮上时,随着旋转时间t(min)与你离开地面的高度h(m)之间的关系如图,你能填写下表吗?[]
时间/min 0 1 2[] 3 4 5
高度/m
新课:
问题:(1)如图是某日的气温变化图。
(5) 这张图告诉我们哪些信息?
(6) 这张图是怎样来展示这天各时刻的温度和刻画这铁的气温变化规律的?
(2)收音机上的刻度盘的波长和频率分别是用米(m)和赫兹(KHz)为单位标刻的,下表中是一些对应的数:
波长l(m) 300 500 600 1000[][] 1500
频率f(KHz) 1000 600 500 300 200
1 这表告诉我们哪些信息?
2 这张表是怎样刻画波长和频率之间的变化规律的,你能用一个表达式表示出来吗?
一般的,在一个变化过程中,如果有两个变量x和y,并且对于x的每一个确定的值,y都有惟一确定的值与其对应,那么我们就说x是自变量,y是x的函数。如果当x=a时,y=b,那么b叫做当自变量的值为a时的函数值。
范例:例1 判断下列变量之间是不是函数关系:
(1) 长方形的宽一定时,其长与面积;
(2) 等腰三角形的底边长与面积;
(3) 某人的年龄与身高;
活动1:阅读教材7页观察1. 后完成教材8页探究,利用计算器发现变量和函数的关系
思考:自变量是否可以任意取值
例2 一辆汽车的油箱中现有汽油50L,如果不再加油,那么油箱中的油量y(单位:L)随行驶里程x(单位:km)的增加而减少,平均耗油量为0.1L/km。
(1) 写出表示y与x的函数关系式.
(2) 指出自变量x的取值范围.汽车行驶200km时,油箱中还有多少汽油?[]
解:(1)y=50-0.1x
(2)0≤x≤500
(3)x=200,y=30[]
活动2:练习教材练习
小结:
(1)函数概念
(2)自变量,函数值
(3)自变量的取值范围确定
作业:
函数图象
知识目标:学会用图像描述变量的变化规律,会准确地画出函数图象
能力目标:结合函数图象,能体会出函数的变化情况
重点:函数的图象
难点:函数图象的画法
引入:
信息1:下图是一张心电图,
信息2:下图是自动测温仪记录的图象,他反映了北京的春季某天气温T如何随时间的变化二变化,你从图象中得到了什么信息?
新课:
问题:正方形的边长x与面积S的函数关系为S=x2, 你能想到更直观地表示S与x 的关系的方法吗?
一般地,对于一个函数,如果把自变量与函数的每对对应诃子分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象(graph)。
范例:例1 下面的图象反映的过程是小明从家去菜地浇水,有去玉米地锄草,然后回家.其中x表示时间,y表示小名离家的距离.
根据图象回答问题:
(4) 菜地离小明家多远?小明走到菜地用了多少时间?
(5) 小明给菜地浇水用了多少时间?
(6) 菜地离玉米地多远?小明从菜地到玉米地用了多少时间?
(7) 小明给玉米锄草用了多少时间?[]
(8) 玉米地离小名家多远?小明从玉米地走回家的平均速度是多少?
例2 在下列式子中,对于x的每一确定的值,y有唯一的对应值,即y是x的函数,画出这些函数的图象:[]
(1)y=x+0.5; (2) y= (x>0)
解:
[]
活动1: 教材练习1,2题
思考:画函数图象的一般步骤是什么?
小结:(1)什么是函数图象
(2)画函数图象的一般步骤 []
函数的表示方法
教学目标
(一)教学知识点
1.总结函数三种表示方法.
2.了解三种表示方法的优缺点.
3.会根据具体情况选择适当方法.
(二)能力训练要求
1.经历回顾思考,训练提高归纳总结能力.
2.利用数形结合思想,据具体情况选用适当方法解决问题的能力.
(三)情感与价值观要求
1.积极参与活动,提高学习兴趣.
2.形成合作交流意识及独立思考习惯.
教学重点
1.认清函数的不同表示方法,知道各自优缺点.
2.能按具体情况选用适当方法.
教学难点
函数表示方法的应用.
教学方法
归纳─总结,自主─探究,实践─应用.
教具准备
多媒体演示.
教学过程
Ⅰ.提出问题,创设情境
[师]我们在上节课里已经看到或亲自动手用列表格.写式子和画图象的方法表示了一些函数.这三种表示函数的方法分别称为列表法、解析式法和图象法.
那么,请同学们思考一下,从前面的例子看,你认为三种表示函数的方法各有什么优缺点?在遇到具体问题时,该如何选择适当的表示方法呢?
这就是我们这节课要研究的内容.
Ⅱ.导入新课
[师]我们首先思考刚才提出的第一个问题.
[生]从前面所见到的或自己做的例子可以看出.列表法比较直观、准确地表示出函数中两个变量的关系.解析式法则比较准确、全面地表示出了函数中两个变量的关系.至于图象法它则形象、直观地表示出函数中两个变量的关系.
[师]好!这位同学说出了三种表示方法的优点,那么他们又各有什么不足之处呢?
[生]相比较而言,列表法不如解析式法全面,也不如图象法形象;而解析式法却不如列表法直观,不如图象法形象;图象法也不如列表法直观准确,不如解析式法全面.
[师]很好!我们就从全面性、直观性、准确性及形象性四个方面来总结归纳函数三种表示方法的优缺点.请同学们根据自己的看法填表:
表示方法 全面性 准确性 直观性 形象性
列表法 × ∨ ∨ ×
解析式法 ∨ ∨ × ×
图象法 × × ∨ ∨
[师]从所填表中可清楚看到三种表示方法各有优缺点.在遇到实际问题时,就要根据具体情况、具体要求选择适当的表示方法,有时为了全面地认识问题,需要几种方法同时使用.
我们来共同看一个例子.
例:一水库的水位在最近5小时内持续上涨,下表记录了这5小时的水位高度.
t/时 0 1 2 3 4 5 …
y/米 10 10.05 10.10 10.15 10.20 10.25 …
1.由记录表推出这5小时中水位高度y(米)随时间t(时)变化的函数解析式,并画出函数图象.
2.据估计这种上涨的情况还会持续2小时,预测再过2小时水位高度将达到多少米?
分析:记录表中已经通过6组数值反映了时间t与水位y之间的对应关系.我们现在需要从这些数值找出这两个表量之间的一般联系规律,由它写出函数解析式来,再画出函数图象,进而预测水位.
解:1.由表中观察到开始水位高10米,以后每隔1小时,水位升高0.05米,这样的规律可以表示为: y=0.05t+10(0≤t≤7)
这个函数的图象如下图所示:
2.再过2小时的水位高度,就是t=5+2=7时,y=0.05t+10的函数值,从解析式容易算出:y=0.05×7+10=10.35
从函数图象也能得出这个值数.
2小时后,预计水位高10.35米.
[师]就上面的例子中我提几个问题大家思考:
1.函数自变量t的取值范围:0≤t≤7是如何确定的?
2.2小时后的水位高是通过解析式求出的呢,还是从函数图象估算出的好?
3.函数的三种表示方法之间是否可以转化?
[生]1.从题目中可以看出水库水位在5小时内持续上涨情况,且估计这种上涨情况还会持续2小时,所以自变量t的取值范围取0≤t≤7,超出了这个范围,情况将难以预计.
2.2小时后水位高通过解析式求准确,通过图象估算直接、方便.就这个题目来说,2小时后水位高本身就是一种估算,但为了准确而言,我认为还是通过解析式求出较好.
3.从这个例子可以看出函数的三种不同表示法可以转化,因为题目中只给出了列表法,而我们通过分析求出解析式并画出了图象,所以我认为可以相互转化.
[师]非常好!我们现在就利用发现和总结的经验,搞个尝试性练习好吗?
尝试练习:
1.用列表法与解析式法表示n边形的内角和m是边数n的函数.
2.用解析式与图象法表示等边三角形周长L是边长a的函数.
解析:1.因为n表示的是多边形的边数,所以,n是大于等于3的自然数.
n 3 4 5 6 …
m 180 360 540 720 …
由表可看出,三角形内角和为180°,边数每增加1条,内角和度数就增加180°.故此m、n函数关系可表示为:
m=(n-2)·180° (n≥3的自然数).
2.因为等边三角形的周长L是边长a的3倍.所以周长L与边长a的函数关系可表示为:
L=3a (a>0)
我们可以用描点法来画出函数L=3a的图象.
列表:
a … 1 2 3 4 …
L … 3 6 9 12 …
描点、连线:
Ⅲ.随堂练习
甲车速度为20米/秒,乙车速度为25米/秒.现甲车在乙车前面500米,设x秒后两车之间的距离为y米.求y随x(0≤x≤100)变化的函数解析式,并画出函数图象.
解:由题意可知:x秒后两车行驶路程分别是:
甲车为:20x 乙车为:25x
两车行驶路程差为:25x-20x=5x
两车之间距离为:500-5x
所以:y随x变化的函数关系式为:
y=500-5x 0≤x≤100
用描点法画图:
x … 10 20 30 40
y … 450 400 350 300
x 50 60 70 80 …
y 250 200 150 100 …
Ⅳ.课时小结
通过本节课学习,我们认识了函数的三种不同的表示方法,并归纳总结出三种表示方法的优缺点,学会根据实际情况和具体要求选择适当的表示方法来解决相关问题,进一步知道了函数三种不同表示方法之间可以转化,为下面学习数形结合的函数做好了准备.
Ⅴ.课后作业
板书设计
函数表示方法一、函数的三种表示方法二、不同表示方法的优缺点三、不同表示方法的具体选择四、随堂练习
教学反思:
感谢您下载使用【班海】教学资源。班海——老师们都在免费用的数学作业精细批改微信小程序!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
19.1 函数
变量
知识目标:理解变量与函数概念以及相互之间的关系
能力目标:增强对变量的理解
情感目标:渗透事物是运动的,运动是有规律的辩证思想
重点:变量与常量
难点:对变量的判断
引入:
信息1:当你坐在摩天轮上时,想一想,随着时间的变化,你离开地面的高度是如何变化的?
信息2:汽车以60km/h的速度匀速前进,行驶里程为skm,行驶的时间为th,先填写下面的表格,在试用含t的式子表示s.
t/m 1 2 3 4 [] 5
s/km [] []
[]
新课:
问题:(1)每张电影票的售价为10元,如果早场售出票150张,日场售出票205张,晚场售出票310张,三场电影的票房收入各多少元?设一场电影受出票x张,票房收入为y元,怎样用含x的式子表示y []
(2)在一根弹簧的下端悬挂中重物,改变并记录重物的质量,观察并记录弹簧长度的变化规律,如果弹簧原长10cm,每1kg重物使弹簧伸长0. 5cm,怎样用含重物质量 m(单位:kg)的式子表示受力后弹簧长度l(单位:cm)?
(3)要画一个面积为10cm2的圆,圆的半径应取多少?圆的面积为20cm2呢?怎样用含圆面积S的式子表示圆的半径r
(4)用10m长的绳子围成长方形,试改变长方形的长度,观察长方形的面积怎样变化。记录不同的长方形的长度值,计算相应的长方形面积的值,探索它们的变化规律,设长方形的长为xm,面积为Sm2,怎样用含x的式子表示S?
在一个变化过程中,我们称数值发生变化的量为变量(variable).数值始终不变的量为常量。
指出上述问题中的变量和常量。
范例:写出下列各问题中所满足的关系式,并指出各个关系式中,哪些量是变量,哪些量是常量?
(1) 用总长为60m的篱笆围成矩形场地,求矩形的面积S(m2)与一边长x(m)之间的关系式;
(2) 购买单价是0.4元的铅笔,总金额y(元)与购买的铅笔的数量n(支)的关系;
(3) 运动员在4000m一圈的跑道上训练,他跑一圈所用的时间t(s)与跑步的速度v(m/s)的关系;
(4) 银行规定:五年期存款的年利率为2.79%,则某人存入x元本金与所得的本息和y(元)之间的关系。[]
活动:1.分别指出下列各式中的常量与变量.
(1) 圆的面积公式S=πr2;
(2) 正方形的l=4a;
(3) 大米的单价为2.50元/千克,则购买的大米的数量x(kg)与金额与金额y的关系为y=2.5x.
2.写出下列问题的关系式,并指出不、常量和变量.[]
(1) 某种活期储蓄的月利率为0.16%,存入10000元本金,按国家规定,取款时,应缴纳利息部分的20%的利息税,求这种活期储蓄扣除利息税后实得的本息和y(元)与所存月数x之间的关系式.
(2) 如图,每个图中是由若干个盆花组成的图案,每条边(包括两个顶点)有n盆花,每个图案的花盆总数是S,求S与n之间的关系式.
思考:怎样列变量之间的关系式?
小结:变量与常量
作业:
函数
知识目标:理解函数的概念,能准确识别出函数关系中的自变量和函数
能力目标:会用变化的量描述事物
情感目标:回用运动的观点观察事物,分析事物
重点:函数的概念
难点:函数的概念
教学媒体:多媒体电脑,计算器
教学说明:注意区分函数与非函数的关系,学会确定自变量的取值范围
教学设计:
引入:
信息1:小明在14岁生日时,看到他爸爸为他记录的以前各年周岁时体重数值表,你能看出小明各周岁时体重是如何变化的吗?
周岁 1 2 3 4 5 6 7 8[] 9 10 11 12 13
体重(kg) 9.3 11.8 13.5[] 15.4 16.7 18.0 19.6 21.5 23.2[] 25 27.6 30.2 32.5
信息2:当你坐在摩天轮上时,随着旋转时间t(min)与你离开地面的高度h(m)之间的关系如图,你能填写下表吗?[]
时间/min 0 1 2[] 3 4 5
高度/m
新课:
问题:(1)如图是某日的气温变化图。
(5) 这张图告诉我们哪些信息?
(6) 这张图是怎样来展示这天各时刻的温度和刻画这铁的气温变化规律的?
(2)收音机上的刻度盘的波长和频率分别是用米(m)和赫兹(KHz)为单位标刻的,下表中是一些对应的数:
波长l(m) 300 500 600 1000[][] 1500
频率f(KHz) 1000 600 500 300 200
1 这表告诉我们哪些信息?
2 这张表是怎样刻画波长和频率之间的变化规律的,你能用一个表达式表示出来吗?
一般的,在一个变化过程中,如果有两个变量x和y,并且对于x的每一个确定的值,y都有惟一确定的值与其对应,那么我们就说x是自变量,y是x的函数。如果当x=a时,y=b,那么b叫做当自变量的值为a时的函数值。
范例:例1 判断下列变量之间是不是函数关系:
(1) 长方形的宽一定时,其长与面积;
(2) 等腰三角形的底边长与面积;
(3) 某人的年龄与身高;
活动1:阅读教材7页观察1. 后完成教材8页探究,利用计算器发现变量和函数的关系
思考:自变量是否可以任意取值
例2 一辆汽车的油箱中现有汽油50L,如果不再加油,那么油箱中的油量y(单位:L)随行驶里程x(单位:km)的增加而减少,平均耗油量为0.1L/km。
(1) 写出表示y与x的函数关系式.
(2) 指出自变量x的取值范围.汽车行驶200km时,油箱中还有多少汽油?[]
解:(1)y=50-0.1x
(2)0≤x≤500
(3)x=200,y=30[]
活动2:练习教材练习
小结:
(1)函数概念
(2)自变量,函数值
(3)自变量的取值范围确定
作业:
函数图象
知识目标:学会用图像描述变量的变化规律,会准确地画出函数图象
能力目标:结合函数图象,能体会出函数的变化情况
重点:函数的图象
难点:函数图象的画法
引入:
信息1:下图是一张心电图,
信息2:下图是自动测温仪记录的图象,他反映了北京的春季某天气温T如何随时间的变化二变化,你从图象中得到了什么信息?
新课:
问题:正方形的边长x与面积S的函数关系为S=x2, 你能想到更直观地表示S与x 的关系的方法吗?
一般地,对于一个函数,如果把自变量与函数的每对对应诃子分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象(graph)。
范例:例1 下面的图象反映的过程是小明从家去菜地浇水,有去玉米地锄草,然后回家.其中x表示时间,y表示小名离家的距离.
根据图象回答问题:
(4) 菜地离小明家多远?小明走到菜地用了多少时间?
(5) 小明给菜地浇水用了多少时间?
(6) 菜地离玉米地多远?小明从菜地到玉米地用了多少时间?
(7) 小明给玉米锄草用了多少时间?[]
(8) 玉米地离小名家多远?小明从玉米地走回家的平均速度是多少?
例2 在下列式子中,对于x的每一确定的值,y有唯一的对应值,即y是x的函数,画出这些函数的图象:[]
(1)y=x+0.5; (2) y= (x>0)
解:
[]
活动1: 教材练习1,2题
思考:画函数图象的一般步骤是什么?
小结:(1)什么是函数图象
(2)画函数图象的一般步骤 []
函数的表示方法
教学目标
(一)教学知识点
1.总结函数三种表示方法.
2.了解三种表示方法的优缺点.
3.会根据具体情况选择适当方法.
(二)能力训练要求
1.经历回顾思考,训练提高归纳总结能力.
2.利用数形结合思想,据具体情况选用适当方法解决问题的能力.
(三)情感与价值观要求
1.积极参与活动,提高学习兴趣.
2.形成合作交流意识及独立思考习惯.
教学重点
1.认清函数的不同表示方法,知道各自优缺点.
2.能按具体情况选用适当方法.
教学难点
函数表示方法的应用.
教学方法
归纳─总结,自主─探究,实践─应用.
教具准备
多媒体演示.
教学过程
Ⅰ.提出问题,创设情境
[师]我们在上节课里已经看到或亲自动手用列表格.写式子和画图象的方法表示了一些函数.这三种表示函数的方法分别称为列表法、解析式法和图象法.
那么,请同学们思考一下,从前面的例子看,你认为三种表示函数的方法各有什么优缺点?在遇到具体问题时,该如何选择适当的表示方法呢?
这就是我们这节课要研究的内容.
Ⅱ.导入新课
[师]我们首先思考刚才提出的第一个问题.
[生]从前面所见到的或自己做的例子可以看出.列表法比较直观、准确地表示出函数中两个变量的关系.解析式法则比较准确、全面地表示出了函数中两个变量的关系.至于图象法它则形象、直观地表示出函数中两个变量的关系.
[师]好!这位同学说出了三种表示方法的优点,那么他们又各有什么不足之处呢?
[生]相比较而言,列表法不如解析式法全面,也不如图象法形象;而解析式法却不如列表法直观,不如图象法形象;图象法也不如列表法直观准确,不如解析式法全面.
[师]很好!我们就从全面性、直观性、准确性及形象性四个方面来总结归纳函数三种表示方法的优缺点.请同学们根据自己的看法填表:
表示方法 全面性 准确性 直观性 形象性
列表法 × ∨ ∨ ×
解析式法 ∨ ∨ × ×
图象法 × × ∨ ∨
[师]从所填表中可清楚看到三种表示方法各有优缺点.在遇到实际问题时,就要根据具体情况、具体要求选择适当的表示方法,有时为了全面地认识问题,需要几种方法同时使用.
我们来共同看一个例子.
例:一水库的水位在最近5小时内持续上涨,下表记录了这5小时的水位高度.
t/时 0 1 2 3 4 5 …
y/米 10 10.05 10.10 10.15 10.20 10.25 …
1.由记录表推出这5小时中水位高度y(米)随时间t(时)变化的函数解析式,并画出函数图象.
2.据估计这种上涨的情况还会持续2小时,预测再过2小时水位高度将达到多少米?
分析:记录表中已经通过6组数值反映了时间t与水位y之间的对应关系.我们现在需要从这些数值找出这两个表量之间的一般联系规律,由它写出函数解析式来,再画出函数图象,进而预测水位.
解:1.由表中观察到开始水位高10米,以后每隔1小时,水位升高0.05米,这样的规律可以表示为: y=0.05t+10(0≤t≤7)
这个函数的图象如下图所示:
2.再过2小时的水位高度,就是t=5+2=7时,y=0.05t+10的函数值,从解析式容易算出:y=0.05×7+10=10.35
从函数图象也能得出这个值数.
2小时后,预计水位高10.35米.
[师]就上面的例子中我提几个问题大家思考:
1.函数自变量t的取值范围:0≤t≤7是如何确定的?
2.2小时后的水位高是通过解析式求出的呢,还是从函数图象估算出的好?
3.函数的三种表示方法之间是否可以转化?
[生]1.从题目中可以看出水库水位在5小时内持续上涨情况,且估计这种上涨情况还会持续2小时,所以自变量t的取值范围取0≤t≤7,超出了这个范围,情况将难以预计.
2.2小时后水位高通过解析式求准确,通过图象估算直接、方便.就这个题目来说,2小时后水位高本身就是一种估算,但为了准确而言,我认为还是通过解析式求出较好.
3.从这个例子可以看出函数的三种不同表示法可以转化,因为题目中只给出了列表法,而我们通过分析求出解析式并画出了图象,所以我认为可以相互转化.
[师]非常好!我们现在就利用发现和总结的经验,搞个尝试性练习好吗?
尝试练习:
1.用列表法与解析式法表示n边形的内角和m是边数n的函数.
2.用解析式与图象法表示等边三角形周长L是边长a的函数.
解析:1.因为n表示的是多边形的边数,所以,n是大于等于3的自然数.
n 3 4 5 6 …
m 180 360 540 720 …
由表可看出,三角形内角和为180°,边数每增加1条,内角和度数就增加180°.故此m、n函数关系可表示为:
m=(n-2)·180° (n≥3的自然数).
2.因为等边三角形的周长L是边长a的3倍.所以周长L与边长a的函数关系可表示为:
L=3a (a>0)
我们可以用描点法来画出函数L=3a的图象.
列表:
a … 1 2 3 4 …
L … 3 6 9 12 …
描点、连线:
Ⅲ.随堂练习
甲车速度为20米/秒,乙车速度为25米/秒.现甲车在乙车前面500米,设x秒后两车之间的距离为y米.求y随x(0≤x≤100)变化的函数解析式,并画出函数图象.
解:由题意可知:x秒后两车行驶路程分别是:
甲车为:20x 乙车为:25x
两车行驶路程差为:25x-20x=5x
两车之间距离为:500-5x
所以:y随x变化的函数关系式为:
y=500-5x 0≤x≤100
用描点法画图:
x … 10 20 30 40
y … 450 400 350 300
x 50 60 70 80 …
y 250 200 150 100 …
Ⅳ.课时小结
通过本节课学习,我们认识了函数的三种不同的表示方法,并归纳总结出三种表示方法的优缺点,学会根据实际情况和具体要求选择适当的表示方法来解决相关问题,进一步知道了函数三种不同表示方法之间可以转化,为下面学习数形结合的函数做好了准备.
Ⅴ.课后作业
板书设计
函数表示方法一、函数的三种表示方法二、不同表示方法的优缺点三、不同表示方法的具体选择四、随堂练习
教学反思:
感谢您下载使用【班海】教学资源。班海——老师们都在免费用的数学作业精细批改微信小程序!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
