【班海精品】人教版(新)八下-20.1 数据的集中趋势 第二课时【优质课件】
文档属性
| 名称 | 【班海精品】人教版(新)八下-20.1 数据的集中趋势 第二课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 10:20:43 | ||
图片预览









文档简介
(共45张PPT)
20.1 数据的集中趋势
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
课堂讲解
加权平均数的计算
加权平均数的应用
新课精讲
探索新知
1
知识点
加权平均数的计算
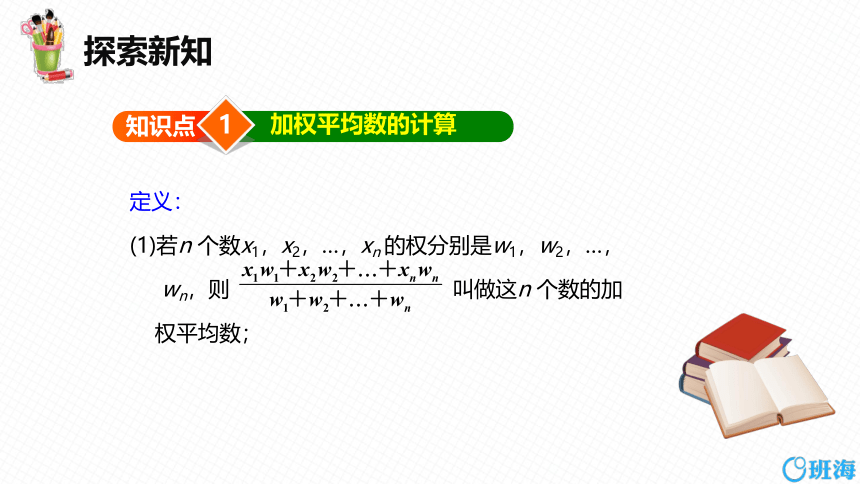
定义:
(1)若n 个数x1,x2,…,xn 的权分别是w1,w2,…,
wn,则 叫做这n 个数的加
权平均数;
探索新知
(2)在求n 个数的平均数时,如果x1出现f1次,x2出现f2次,
…,xk 出现fk 次(这里f1+f2+…+fk=n),那么这n 个
数的平均数 也叫做x1,x2,
…,xk 这k 个数的加权平均数,其中f1,f2,…,fk 分
别叫做x1,x2,…,xk 的权.
探索新知
导引:
把2,3,5分别看作是85分,80分和90分的权,按加权平均数的计算公式计算即可.
∵
∴小王的成绩为86分.
答案:D
探索新知
小王参加某企业招聘测试,他的笔试、面试、技能操作得分分别为85分,80分,90分,若依次按照2∶3∶5的比例确定成绩,则小王的成绩是( )
A.255分 B.84分
C.84.5分 D.86分
例1
D
探索新知
总 结
权的形式有几种,若以比例的形式为权,可直接将比例中的份数作为每个数的权进行计算.
典题精讲
从一组数据中取出a 个x1,b 个x2,c 个x3,组成一个样本,那么这个样本的平均数是( )
A. B.
C. D.
1
B
已知一组数据,其中有4个数的平均数为20,另有16个数的平均数为15,则这20个数的平均数是( )
A.16 B.17.5 C.18 D.20
2
A
探索新知
2
知识点
加权平均数的应用
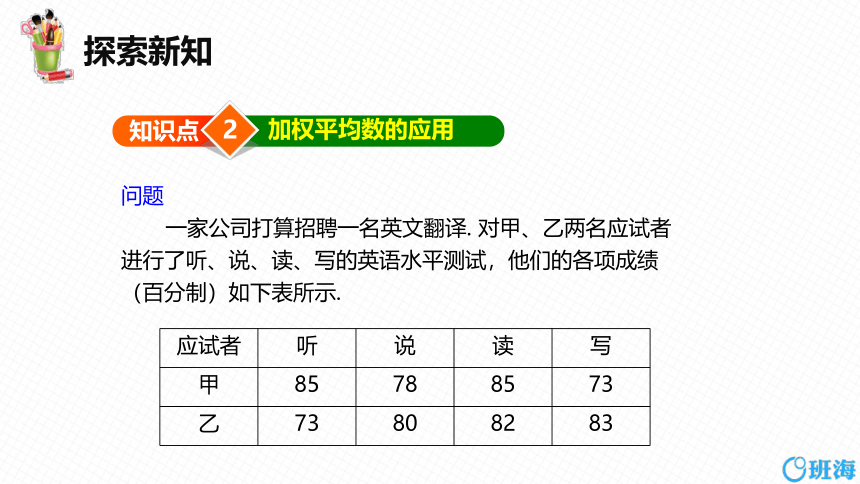
问题
一家公司打算招聘一名英文翻译. 对甲、乙两名应试者进行了听、说、读、写的英语水平测试,他们的各项成绩(百分制)如下表所示.
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
探索新知
如果这家公司想招一名笔译能力较强的翻译,听、说、读、写成绩按照2 : 1 : 3 : 4的比确定,计算两名应试者的平均成绩(百分制).从他们的成绩看,应该录取谁?
对于上述问题,听、说、读、写成绩按照2 : 1 : 3 : 4的
比确定,这说明各项成绩的“重要程度”有所不同,
读、写的成绩比听、说的成绩更加“重要”因此,甲
的平均成绩为
乙的平均成绩为
因为乙的平均成绩比甲高,所以应该录取乙.
探索新知
对于上述问题是根据实际需要对不同类型的数据赋予与其重要程度相应的比重,其中的2,1,3,4分别称为听、说、读、写四项成绩的权 ,相应的平均数79. 5,80. 4分别称为甲和乙的听、说、读、写四项成绩的加权平均数.
探索新知
某跳水队为了解运动员的年龄情况,作了一次年龄调查,结果如 下:13岁8人,14岁16人,15岁24人,16岁2人.求这个跳水队运动员的 平均年龄(结果取整数).
例2
解:
这个跳水队运动员的平均年龄为
探索新知
总 结
平均成绩应该等于总年龄数除以总人数,由于各个年龄段的人数不相同,因此它们的“权”不相同,所以应该用加权平均数公式求解.
探索新知
某一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分.各项成绩均按百分制计,然后再按演讲内容占50%、演讲能力占40%、演讲效果占10%,计算选手的综合成绩 (百分制) .
进入决赛的前两名选手的单项成绩如下表所示,请确定两人的名次.
例3
探索新知
这个问题可以看成是求两名选手三项成绩的加权平均数,50%, 40%, 10%说明演讲内容、演讲能力、演讲效果三项成绩在总成绩中的重要程度,是三项成绩的权.
分析:
选手 演讲内容 演讲能力 演讲效果
A 85 95 95
B 95 85 95
探索新知
选手A的最后得分是
选手B的最后得分是
由上可知选手B 获得第一名,选手A 获得第二名.
解:
探索新知
总 结
用权重解决决策问题的方法:
不同的权重,直接影响最后决策的结果,在实际生活中,我们经常会遇到这类问题,当需要在某个方面要求比较高的时候,往往可以加大这方面的权重,以达到预想的结果.
典题精讲
某公司欲招聘一名公关人员.对甲、乙两位应试者进行了面试和笔试,他们的成绩(百分制)如下表所示.
如果公司认为面试和笔试成绩同等重要,从他们的成绩看,谁将被录取?
如果公司认为,作为公关人员面试成绩应该比笔试成绩更重要,并分别赋 予它们6和4的权,计算甲、乙两人各自的平均成绩,谁将被录取?
1
应试者 面试 笔试
甲 86 90
乙 92 83
典题精讲
(1)甲的平均成绩为 (分),乙的平均成
绩为 (分),因为甲的平均成绩高
于乙的平均成绩,所以候选人甲将被录取.
(2)甲的平均成绩为 (分),乙的
平均成绩为 (分),因为甲的
平均成绩低于乙的平均成绩,所以候选人乙将
被录取.
解:
典题精讲
晨光中学规定学生的学期体育成绩满分为100,其中早锻炼及体育课外活动占 20%,期中考试成绩占30%,期末考试成绩占50% . 小桐的三项成绩(百分制) 依次是95, 90, 85. 小桐这学期的体育成绩是多少?
2
根据题意,
得95×20%+90×30%+85×50%=88.5(分).
所以小桐这学期的体育成绩是88.5分.
解:
典题精讲
超市决定招聘广告策划人员一名,某应聘者三项素质测试的成绩如下表:
3
应用1
用比例表示的“权”
将创新能力、综合知识和语言表达三项测试成绩按5:3:2的比例计入总成绩,则该应聘者的总成绩是________分.
测试项目 创新能力 综合知识 语言表达
测试成绩/分 70 80 92
77.4
典题精讲
某校广播站要招聘1名记者,小亮和小丽报名参加了3项素质测试,成绩如下:
4
写作能力 普通话水平 计算机水平
小亮 90分 75分 51分
小丽 60分 84分 72分
将写作能力、普通话水平、计算机水平这三项的总分由原来按3:5:2计算,变成按5:3:2计算,总分变化情况是( )
A.小丽增加得多 B.小亮增加得多
C.两人成绩不变化 D.变化情况无法确定
B
典题精讲
某校规定学生的学期数学成绩满分为100分,其中研究性学习成绩占40%,期末卷面成绩占60%,小明的两项成绩(百分制)依次是80分,90分,则小明这学期的数学成绩是( )
A.80分 B.82分 C.84分 D.86分
5
应用2
用百分数表示的“权”
D
典题精讲
为了满足顾客的需求,某商场将5 kg奶糖,3 kg酥心糖和2 kg水果糖混合成什锦糖出售.已知奶糖的售价为每千克40元,酥心糖为每千克20元,水果糖为每千克15元,混合后什锦糖的售价应为每千克( )
A.25元 B.28.5元 C.29元 D.34.5元
6
应用3
用频(次)数表示的“权”
C
典题精讲
下列各组数据中,组中值不是10的是( )
A.0≤x<20 B.8≤x<12
C.7≤x<13 D.3≤x<7
7
应用4
用组中值表示的“权”
D
易错提醒
宾馆客房的标价影响入住百分率.下表是某宾馆在近几年旅游周统计的平均数据.在旅游周,要使宾馆客房收入最大,客房标价应选( )
A.160元 B.140元 C.120元 D.100元
B
客房标价/元 160 140 120 100
入住百分率 63.8% 74.3% 84.1% 95%
易错点:求加权平均数时,忽视数据与权的关系导致出错.
学以致用
小试牛刀
对一组数据进行了整理,结果如下表:
1
分组 0≤x<10 10≤x<20
频数 8 12
则这组数据的平均数约是( )
A.10 B.11
C.12 D.16
B
小试牛刀
某老师为了了解学生周末学习时间的情况,在所任班级中随机调查了10名学生,绘成了如图所示的条形统计图,则这10名学生周末学均时间是( )
A.4小时
B.3小时
C.2小时
D.1小时
2
B
小试牛刀
学校准备从甲、乙两位选手中选择一位选手代表学校参加所在地区
的汉字听写大赛,学校对两位选手从表达能力、阅读理解、综合素
质和汉字听写四个方面进行了测试,他们各自的成绩(百分制)如下表:
选手 表达能力 阅读理解 综合素质 汉字听写
甲 85 78 85 73
乙 73 80 82 83
小试牛刀
(1)由表中成绩已算得甲的平均成绩为80.25,请计算乙的平均成
绩,从他们的这一成绩看,应选派谁?
(2)如果表达能力、阅读理解、综合素质和汉字听写分别赋予它们
2,1,3和4的权,请分别计算两位选手的平均成绩,从他们的
这一成绩看,应选派谁?
小试牛刀
(1)乙的平均成绩为 =79.5.
因为80.25>79.5,所以应选派甲.
(2)甲的平均成绩为 =79.5,
乙的平均成绩为 =80.4.
因为79.5<80.4,所以应选派乙.
解:
小试牛刀
4 某公司对员工的月收入统计如下:
由于公司的效益不断提高,公司领导决定提高员工的
月收入,提高后员工的月收入情况如下:
(1)求该公司员工原平均月收入和提高后的平均月收入;
(2)员工收入提高后,该公司每月需要多拿出多少元支付员工
的月收入?
收入x/元 3 600≤x<4 000 4 000≤x<4 400 4 400≤x<4 800
人数 12 50 18
收入x/元 4 000≤x<4 400 4 400≤x<4 800 4 800≤x<5 200
人数 12 50 18
小试牛刀
(1)x原= =4 230(元);
x提= =4 630(元).
答:该公司员工原平均月收入和提高后的平均月收
入分别为4 230元和4 630元.
(2)(4 630-4 230)×(12+50+18)=400×80=32 000(元).
答:员工收入提高后,该公司每月需要多拿出32 000
元支付员工的月收入.
解:
-
-
小试牛刀
某校学生会决定从三名学生会干事中选拔一名干部,
对甲、乙、丙三名候选人进行了笔试和面试,三人的
测试成绩如下表所示:
测试项目 测试成绩/分 甲 乙 丙
笔试 75 80 90
面试 93 70 68
小试牛刀
根据录用程序,学校组织200名学生采用投票推荐的方式,对三人进行民主测评,三人得票率(没有弃权票,每名学生只能推荐1人)如扇形统计图所示,每得一票记1分.
(1)分别计算三人民主测评的得分;
(2)根据实际需要,学校将笔试、面试、民主测评三项得分按4∶3∶3的比例确定个人成绩,三人中谁的得分最高?
小试牛刀
(1)甲民主测评的得分是200×25%=50(分);
乙民主测评的得分是200×40%=80(分);
丙民主测评的得分是200×35%=70(分).
(2)甲的成绩是(75×4+93×3+50×3)÷(4+3+3)=
729÷10=72.9(分),
乙的成绩是(80×4+70×3+80×3)÷(4+3+3)=
770÷10=77(分),
丙的成绩是(90×4+68×3+70×3)÷(4+3+3)=
774÷10=77.4(分),
因为77.4>77>72.9,所以丙的得分最高.
解:
小试牛刀
“五一”期间,新华商场贴出促销海报,内容如图①.在商场活动
期间,王莉和同组同学随机调查了部分参加活动的顾客,统计
了200人次的摸奖情况,绘制成如图②所示的统计图.
(1)补全统计图;
(2)求所调查的200人次
摸奖的获奖率;
(3)若商场每天约有2 000人次摸奖,请估算商场一天
送出的购物券总金额是多少元.
小试牛刀
(1)补全统计图,如图所示.
(2)摸奖的获奖率:
×100%=39%.
(3)x= =6.675(元).
6.675×2 000=13 350(元).
答:估计商场一天送出的购物券总金额是13 350元.
解:
-
课堂小结
课堂小结
算术平均数与加权平均数的联系与区别:
联系:若各个数据的权相同,则加权平均数就是算术平
均数,因而可看出算术平均数实质上是加权平均
数的一种特例.
区别:算术平均数是指一组数据的和除以数据个数,加
权平均数是指在实际问题中,一组数据的“重要
程度”未必相同,即各个数据的权未必相同,因
而在计算上与算术平均数有所不同.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
20.1 数据的集中趋势
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
课堂讲解
加权平均数的计算
加权平均数的应用
新课精讲
探索新知
1
知识点
加权平均数的计算
定义:
(1)若n 个数x1,x2,…,xn 的权分别是w1,w2,…,
wn,则 叫做这n 个数的加
权平均数;
探索新知
(2)在求n 个数的平均数时,如果x1出现f1次,x2出现f2次,
…,xk 出现fk 次(这里f1+f2+…+fk=n),那么这n 个
数的平均数 也叫做x1,x2,
…,xk 这k 个数的加权平均数,其中f1,f2,…,fk 分
别叫做x1,x2,…,xk 的权.
探索新知
导引:
把2,3,5分别看作是85分,80分和90分的权,按加权平均数的计算公式计算即可.
∵
∴小王的成绩为86分.
答案:D
探索新知
小王参加某企业招聘测试,他的笔试、面试、技能操作得分分别为85分,80分,90分,若依次按照2∶3∶5的比例确定成绩,则小王的成绩是( )
A.255分 B.84分
C.84.5分 D.86分
例1
D
探索新知
总 结
权的形式有几种,若以比例的形式为权,可直接将比例中的份数作为每个数的权进行计算.
典题精讲
从一组数据中取出a 个x1,b 个x2,c 个x3,组成一个样本,那么这个样本的平均数是( )
A. B.
C. D.
1
B
已知一组数据,其中有4个数的平均数为20,另有16个数的平均数为15,则这20个数的平均数是( )
A.16 B.17.5 C.18 D.20
2
A
探索新知
2
知识点
加权平均数的应用
问题
一家公司打算招聘一名英文翻译. 对甲、乙两名应试者进行了听、说、读、写的英语水平测试,他们的各项成绩(百分制)如下表所示.
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
探索新知
如果这家公司想招一名笔译能力较强的翻译,听、说、读、写成绩按照2 : 1 : 3 : 4的比确定,计算两名应试者的平均成绩(百分制).从他们的成绩看,应该录取谁?
对于上述问题,听、说、读、写成绩按照2 : 1 : 3 : 4的
比确定,这说明各项成绩的“重要程度”有所不同,
读、写的成绩比听、说的成绩更加“重要”因此,甲
的平均成绩为
乙的平均成绩为
因为乙的平均成绩比甲高,所以应该录取乙.
探索新知
对于上述问题是根据实际需要对不同类型的数据赋予与其重要程度相应的比重,其中的2,1,3,4分别称为听、说、读、写四项成绩的权 ,相应的平均数79. 5,80. 4分别称为甲和乙的听、说、读、写四项成绩的加权平均数.
探索新知
某跳水队为了解运动员的年龄情况,作了一次年龄调查,结果如 下:13岁8人,14岁16人,15岁24人,16岁2人.求这个跳水队运动员的 平均年龄(结果取整数).
例2
解:
这个跳水队运动员的平均年龄为
探索新知
总 结
平均成绩应该等于总年龄数除以总人数,由于各个年龄段的人数不相同,因此它们的“权”不相同,所以应该用加权平均数公式求解.
探索新知
某一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分.各项成绩均按百分制计,然后再按演讲内容占50%、演讲能力占40%、演讲效果占10%,计算选手的综合成绩 (百分制) .
进入决赛的前两名选手的单项成绩如下表所示,请确定两人的名次.
例3
探索新知
这个问题可以看成是求两名选手三项成绩的加权平均数,50%, 40%, 10%说明演讲内容、演讲能力、演讲效果三项成绩在总成绩中的重要程度,是三项成绩的权.
分析:
选手 演讲内容 演讲能力 演讲效果
A 85 95 95
B 95 85 95
探索新知
选手A的最后得分是
选手B的最后得分是
由上可知选手B 获得第一名,选手A 获得第二名.
解:
探索新知
总 结
用权重解决决策问题的方法:
不同的权重,直接影响最后决策的结果,在实际生活中,我们经常会遇到这类问题,当需要在某个方面要求比较高的时候,往往可以加大这方面的权重,以达到预想的结果.
典题精讲
某公司欲招聘一名公关人员.对甲、乙两位应试者进行了面试和笔试,他们的成绩(百分制)如下表所示.
如果公司认为面试和笔试成绩同等重要,从他们的成绩看,谁将被录取?
如果公司认为,作为公关人员面试成绩应该比笔试成绩更重要,并分别赋 予它们6和4的权,计算甲、乙两人各自的平均成绩,谁将被录取?
1
应试者 面试 笔试
甲 86 90
乙 92 83
典题精讲
(1)甲的平均成绩为 (分),乙的平均成
绩为 (分),因为甲的平均成绩高
于乙的平均成绩,所以候选人甲将被录取.
(2)甲的平均成绩为 (分),乙的
平均成绩为 (分),因为甲的
平均成绩低于乙的平均成绩,所以候选人乙将
被录取.
解:
典题精讲
晨光中学规定学生的学期体育成绩满分为100,其中早锻炼及体育课外活动占 20%,期中考试成绩占30%,期末考试成绩占50% . 小桐的三项成绩(百分制) 依次是95, 90, 85. 小桐这学期的体育成绩是多少?
2
根据题意,
得95×20%+90×30%+85×50%=88.5(分).
所以小桐这学期的体育成绩是88.5分.
解:
典题精讲
超市决定招聘广告策划人员一名,某应聘者三项素质测试的成绩如下表:
3
应用1
用比例表示的“权”
将创新能力、综合知识和语言表达三项测试成绩按5:3:2的比例计入总成绩,则该应聘者的总成绩是________分.
测试项目 创新能力 综合知识 语言表达
测试成绩/分 70 80 92
77.4
典题精讲
某校广播站要招聘1名记者,小亮和小丽报名参加了3项素质测试,成绩如下:
4
写作能力 普通话水平 计算机水平
小亮 90分 75分 51分
小丽 60分 84分 72分
将写作能力、普通话水平、计算机水平这三项的总分由原来按3:5:2计算,变成按5:3:2计算,总分变化情况是( )
A.小丽增加得多 B.小亮增加得多
C.两人成绩不变化 D.变化情况无法确定
B
典题精讲
某校规定学生的学期数学成绩满分为100分,其中研究性学习成绩占40%,期末卷面成绩占60%,小明的两项成绩(百分制)依次是80分,90分,则小明这学期的数学成绩是( )
A.80分 B.82分 C.84分 D.86分
5
应用2
用百分数表示的“权”
D
典题精讲
为了满足顾客的需求,某商场将5 kg奶糖,3 kg酥心糖和2 kg水果糖混合成什锦糖出售.已知奶糖的售价为每千克40元,酥心糖为每千克20元,水果糖为每千克15元,混合后什锦糖的售价应为每千克( )
A.25元 B.28.5元 C.29元 D.34.5元
6
应用3
用频(次)数表示的“权”
C
典题精讲
下列各组数据中,组中值不是10的是( )
A.0≤x<20 B.8≤x<12
C.7≤x<13 D.3≤x<7
7
应用4
用组中值表示的“权”
D
易错提醒
宾馆客房的标价影响入住百分率.下表是某宾馆在近几年旅游周统计的平均数据.在旅游周,要使宾馆客房收入最大,客房标价应选( )
A.160元 B.140元 C.120元 D.100元
B
客房标价/元 160 140 120 100
入住百分率 63.8% 74.3% 84.1% 95%
易错点:求加权平均数时,忽视数据与权的关系导致出错.
学以致用
小试牛刀
对一组数据进行了整理,结果如下表:
1
分组 0≤x<10 10≤x<20
频数 8 12
则这组数据的平均数约是( )
A.10 B.11
C.12 D.16
B
小试牛刀
某老师为了了解学生周末学习时间的情况,在所任班级中随机调查了10名学生,绘成了如图所示的条形统计图,则这10名学生周末学均时间是( )
A.4小时
B.3小时
C.2小时
D.1小时
2
B
小试牛刀
学校准备从甲、乙两位选手中选择一位选手代表学校参加所在地区
的汉字听写大赛,学校对两位选手从表达能力、阅读理解、综合素
质和汉字听写四个方面进行了测试,他们各自的成绩(百分制)如下表:
选手 表达能力 阅读理解 综合素质 汉字听写
甲 85 78 85 73
乙 73 80 82 83
小试牛刀
(1)由表中成绩已算得甲的平均成绩为80.25,请计算乙的平均成
绩,从他们的这一成绩看,应选派谁?
(2)如果表达能力、阅读理解、综合素质和汉字听写分别赋予它们
2,1,3和4的权,请分别计算两位选手的平均成绩,从他们的
这一成绩看,应选派谁?
小试牛刀
(1)乙的平均成绩为 =79.5.
因为80.25>79.5,所以应选派甲.
(2)甲的平均成绩为 =79.5,
乙的平均成绩为 =80.4.
因为79.5<80.4,所以应选派乙.
解:
小试牛刀
4 某公司对员工的月收入统计如下:
由于公司的效益不断提高,公司领导决定提高员工的
月收入,提高后员工的月收入情况如下:
(1)求该公司员工原平均月收入和提高后的平均月收入;
(2)员工收入提高后,该公司每月需要多拿出多少元支付员工
的月收入?
收入x/元 3 600≤x<4 000 4 000≤x<4 400 4 400≤x<4 800
人数 12 50 18
收入x/元 4 000≤x<4 400 4 400≤x<4 800 4 800≤x<5 200
人数 12 50 18
小试牛刀
(1)x原= =4 230(元);
x提= =4 630(元).
答:该公司员工原平均月收入和提高后的平均月收
入分别为4 230元和4 630元.
(2)(4 630-4 230)×(12+50+18)=400×80=32 000(元).
答:员工收入提高后,该公司每月需要多拿出32 000
元支付员工的月收入.
解:
-
-
小试牛刀
某校学生会决定从三名学生会干事中选拔一名干部,
对甲、乙、丙三名候选人进行了笔试和面试,三人的
测试成绩如下表所示:
测试项目 测试成绩/分 甲 乙 丙
笔试 75 80 90
面试 93 70 68
小试牛刀
根据录用程序,学校组织200名学生采用投票推荐的方式,对三人进行民主测评,三人得票率(没有弃权票,每名学生只能推荐1人)如扇形统计图所示,每得一票记1分.
(1)分别计算三人民主测评的得分;
(2)根据实际需要,学校将笔试、面试、民主测评三项得分按4∶3∶3的比例确定个人成绩,三人中谁的得分最高?
小试牛刀
(1)甲民主测评的得分是200×25%=50(分);
乙民主测评的得分是200×40%=80(分);
丙民主测评的得分是200×35%=70(分).
(2)甲的成绩是(75×4+93×3+50×3)÷(4+3+3)=
729÷10=72.9(分),
乙的成绩是(80×4+70×3+80×3)÷(4+3+3)=
770÷10=77(分),
丙的成绩是(90×4+68×3+70×3)÷(4+3+3)=
774÷10=77.4(分),
因为77.4>77>72.9,所以丙的得分最高.
解:
小试牛刀
“五一”期间,新华商场贴出促销海报,内容如图①.在商场活动
期间,王莉和同组同学随机调查了部分参加活动的顾客,统计
了200人次的摸奖情况,绘制成如图②所示的统计图.
(1)补全统计图;
(2)求所调查的200人次
摸奖的获奖率;
(3)若商场每天约有2 000人次摸奖,请估算商场一天
送出的购物券总金额是多少元.
小试牛刀
(1)补全统计图,如图所示.
(2)摸奖的获奖率:
×100%=39%.
(3)x= =6.675(元).
6.675×2 000=13 350(元).
答:估计商场一天送出的购物券总金额是13 350元.
解:
-
课堂小结
课堂小结
算术平均数与加权平均数的联系与区别:
联系:若各个数据的权相同,则加权平均数就是算术平
均数,因而可看出算术平均数实质上是加权平均
数的一种特例.
区别:算术平均数是指一组数据的和除以数据个数,加
权平均数是指在实际问题中,一组数据的“重要
程度”未必相同,即各个数据的权未必相同,因
而在计算上与算术平均数有所不同.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
