【班海精品】人教版(新)八下-17.1 勾股定理 第三课时【优质课件】
文档属性
| 名称 | 【班海精品】人教版(新)八下-17.1 勾股定理 第三课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 10:20:43 | ||
图片预览










文档简介
(共40张PPT)
17.1 勾股定理
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
某拍卖行贴出了如下的一个土地拍卖广告:
如下图,有面积为560英亩的土地拍卖,土地共分三个正方形,面积分别为74英亩、116英亩、370英亩.三个正方形恰好围着一个池塘,如果有人能
计算出池塘的准确面积.则
池塘不计入土地价钱白白奉
送.英国数学家巴尔教授曾
经巧妙地解答了这个问题,
你能解决吗
新课精讲
探索新知
1
知识点
用勾股定理在数轴上表示数
我们知道数轴上的点有的表示有理数,有的表示无理
数,你能在数轴上画出表示 的点吗?
如果能画出长为 的线段,就能在数轴上画出表示
的点.容易知道,长为 的线段是两条直角边的长都
为1的直角三角形的斜边.长为 的线段能是直角边的长
为正整数的直角三角形的斜边吗?
探索新知
利用勾股定理,可以发现,直角边的长为正整数2, 3的直角三角形的斜边长为 .由此,可以依照如下方法在数轴上画出表示 的点.
如图,在数轴上找出表示3的点A, 则OA=3,过点A作直线l垂直于OA,在l上取点B,使AB = 2,以原点O为圆心,以OB为半径作弧,弧与数轴的交点C 即为表示 的点.
探索新知
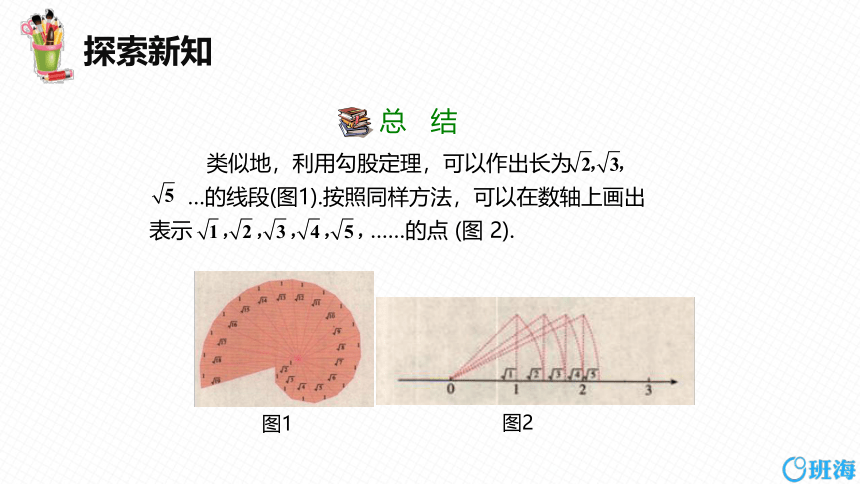
总 结
类似地,利用勾股定理,可以作出长为
…的线段(图1).按照同样方法,可以在数轴上画出
表示 ……的点 (图 2).
图1
图2
探索新知
利用 a= 可以作出.
如图2,先作出与已知线段AB 垂直,
且与已知线段的端点A相交的直线l,
在直线l上以A为端点截取长为2a 的线
段AC,连接BC,则线段BC 即为所求.
如图2,BC就是所求作的线段.
例1 如图1,已知线段AB 的长为a,请作出长为 a 的
段.(保留作图痕迹,不写作法)
图1
图2
导引:
解:
探索新知
总 结
这类问题要作的线段一般是直角三角形的斜边,根据勾股定理由要作的线段确定两直角边的长是解题的关键.
典题精讲
1 在数轴上做出表示 的点.
如图所示.作法:
(1)在数轴上找出表示4的点A,则OA=4;
(2)过A作直线l 垂直于OA;
(3)在直线l上取点B,使AB=1;
(4)以原点O 为圆心,以OB 为半径作弧,弧与
数轴的交点C 即为表示 的点.
解:
典题精讲
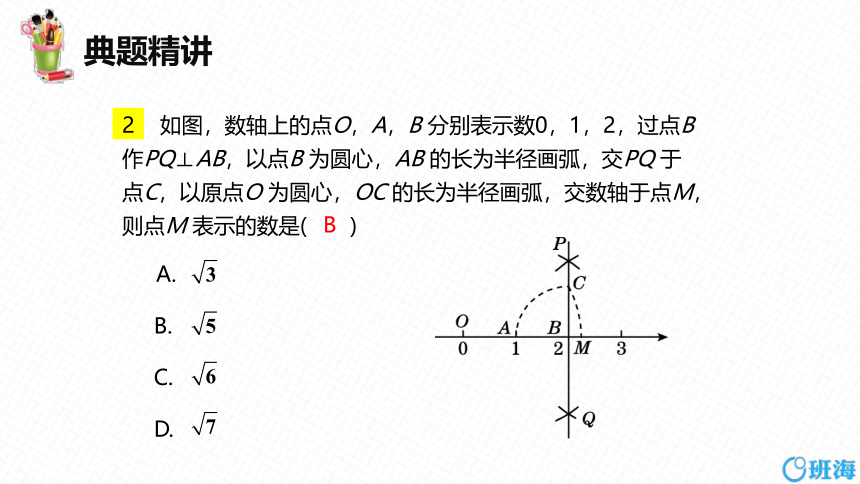
2 如图,数轴上的点O,A,B 分别表示数0,1,2,过点B 作PQ⊥AB,以点B 为圆心,AB 的长为半径画弧,交PQ 于点C,以原点O 为圆心,OC 的长为半径画弧,交数轴于点M,则点M 表示的数是( )
A.
B.
C.
D.
B
典题精讲
3 如图,点C 表示的数是( )
A.1 B. C.1.5 D.
D
典题精讲
如图,在长方形ABCD 中,AB=3,AD=1,AB 在数轴上,若以点A为圆心,对角线AC 的长为半径作弧交数轴于点M,则点M 表示的数为( )
A.2
B. -1
C. -1
D.
4
C
探索新知
2
知识点
用勾股定理解几何问题
例2 如图,在△ABC 中,∠C=60°,AB=14,AC
=10. 求BC 的长.
导引:题中没有直角三角形,可以通
过作高构建直角三角形;过点
A作AD⊥BC 于D,图中会出现
两个直角三角形——Rt△ACD 和Rt△ABD,这两
个直角三角形有一条公共边AD,借助这条公共边,
可建立起直角三角形之间的联系.
探索新知
解:如图,过点A 作AD⊥BC 于D.
∵∠ADC=90°,∠C=60°,∴CD= AC=5.
在Rt△ACD中,
AD
在Rt△ABD中,
BD
∴BC=BD+CD=11+5=16.
探索新知
总 结
利用勾股定理求非直角三角形中线段的长的方法:
作三角形一边上的高,将其转化为两个直角三角形,然后利用勾股定理并结合已知条件,采用推理或列方程的方法解决问题.
典题精讲
1 如图,等边三角形的边长是6.求:
(1)高AD 的长;
(2)这个三角形的面积.
(1)由题意可知,在Rt△ADB 中,
AB=6,BD= BC=3,∠ADB=90°.
由勾股定理,
得AD=
(2)S△ABC= BC·AD= ×6×3
=
解:
典题精讲
如图是由4个边长为1的正方形构成的“田字格”,只用没有刻度的直尺在这个“田字格”中最多可以作出长度为 的线段________条.
2
8
典题精讲
如图,每个小正方形的边长均为1,则△ABC 中,长为无理
数的边有( )
A.0条
B.1条
C.2条
D.3条
C
典题精讲
4 如图是一张直角三角形的纸片,两直角边AC=6 cm,BC=8 cm,现将△ABC 折叠,使点B 与点A重合,折痕为DE,则BE 的长为( )
A.4 cm
B.5 cm
C.6 cm
D.10 cm
B
易错提醒
如图,把长方形纸条ABCD 沿EF,GH 同时折叠,B,C 两点恰好落在AD 边的P 点处,若∠FPH=90°,PF=8,PH=6,则长方形ABCD 的面积为________.
115.2
易错提醒
在Rt△PFH 中,FH=
=10,∴BC=BF+FH+CH=PF+FH+PH=8+10+6=24.设△PFH 的边FH 上的高为h,
则h= =4.8,
∴S长方形ABCD=24×4.8=115.2.
易错提醒
易错点:忽视题目中条件而求不出答案.
解此题时要灵活运用折叠前后对应线段相等,从而求出BC 的长,然后再运用面积法求出△PFH 中FH 边上的高,本题容易因忽视条件而求不出答案.
易错总结:
学以致用
小试牛刀
如图,在平面直角坐标系中,点P 的坐标为(-2,3),以点O 为圆心,以OP 的长为半径画弧,交x 轴的负半轴于点A,则点A 的横坐标介于( )
A.-4和-3之间
B.3和4之间
C.-5和-4之间
D.4和5之间
1
A
小试牛刀
如图,在矩形ABCD 中,BC=8,CD=6,将△ABE 沿BE 折叠,使点A恰好落在对角线BD上F 处,则DE 的长是( )
A.3
B.
C.5
D.
2
C
小试牛刀
如图,在等腰三角形ABC 中,AB=AC,BC 边上的高AD=6 cm,腰AB上的高CE=8 cm,则△ABC 的周长等于________cm.
3
小试牛刀
4 如图,正方形网格中的每个小正方形的边长都是1,
每个小格的顶点叫做格点.以格点为顶点画三角形.
(1)使三角形的三边长分别为 3,2 , .
(2)使三角形的周长为 .
小试牛刀
(1)如图①中的△ABC 为所求的三角形.
(2)如图②中的△ABC的三边长分别为 ,
三角形的周长为 .
解:
小试牛刀
如图,连接BD.因为AB=AD,∠A=60°,
所以∠1=∠ABD= =60°.
所以△ABD是等边三角形.所以BD=8.
又∠1+∠2=150°,则∠2=90°.
设BC=x,则CD=16-x,
由勾股定理得x 2=82+(16-x )2.
解得x=10.所以BC=10,CD=6.
5 如图,在四边形ABCD 中,AB=AD=8,
∠A=60°,∠D=150°,四边形的周长
为32,求BC 和CD 的长度.
解:
小试牛刀
6 [阅读理解]
如图,在△ABC中,BC=a,CA=b,AB=c.
(1)若∠C 为直角,则a 2+b 2=c 2;
(2)若∠C 为锐角,则a 2+b 2与c 2的关系为a 2+b 2>c 2;
(3)若∠C 为钝角,试推导a 2+b 2与c 2的关系.
[探究问题]在△ABC 中,BC=a=3,CA=b=4,
AB=c,若△ABC 是钝角三角形,求第三边c 的取值范围.
小试牛刀
[阅读理解](3)如图所示,作AD⊥BC 交BC 的延长线于D,则BD=BC+CD=a+CD,
在Rt△ABD 中,AD 2=AB 2-BD 2.
在Rt△ACD 中,AD 2=AC 2-CD 2,
∴AB 2-BD 2=AC 2-CD 2,
∴c 2-(a+CD )2=b 2-CD 2,
整理得a 2+b 2=c 2-2a ·CD.
∵a>0,CD>0,∴a 2+b 2<c 2;
解:
小试牛刀
[探究问题]当∠C 为钝角时, <c<a+b,
∵a=3,b=4,
∴ <c<3+4,即5<c<7;
当∠B 为钝角时,b-a<c< ,
∵a=3,b=4,
∴4-3<c< ,即1<c< .
综上所述第三边c的取值范围为5<c<7或1<c< .
小试牛刀
7 如图,在Rt△ABC中,∠C=90°,点D 是AB 的中点,点E,F 分别为AC,BC 的中点,DE⊥DF.求证:AE 2+BF 2=EF 2.
小试牛刀
如图,延长ED 至点G,使DG=ED,连接BG,FG.
在△ADE 和△BDG 中,
AD=DB,∠1=∠2,ED=DG,
∴△ADE ≌△BDG (SAS).
∴AE=BG,∠3=∠4.
又∵∠4+∠5=90°,∴∠3+∠5=90°.
又∵DF⊥EG,DE=DG,∴FG=EF.
在Rt△FBG 中,BG 2+BF 2=FG 2,
即AE 2+BF 2=EF 2.
证明:
课堂小结
课堂小结
1.勾股定理与三角形三边平方关系的综合应用:
单一应用:先由三角形三边平方关系得出直角三角形后,再求这个直角三角形的角度和面积:
综合应用:先用勾股定理求出三角形的边长,再由三角形平方关系确定三角形的形状,进而解决其他问题;
逆向应用:如果一个三角形两条较小边长的平方和不等于最大边长的平方,那么这个三角形就不是直角三角形.
课堂小结
2.应用勾股定理解题的方法:
(1)添线应用,即题中无直角三角形,可以通过作垂线,构
造直角三角形,应用勾股定理求解;
(2)借助方程应用,即题中虽有直角三角形,但已知线段的
长不完全是直角三角形的边长,可通过设未知数,构建
方程,解答计算问题;
(3)建模应用,即将实际问题建立直角三角形模型,通过勾
股定理解决实际问题.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
17.1 勾股定理
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
某拍卖行贴出了如下的一个土地拍卖广告:
如下图,有面积为560英亩的土地拍卖,土地共分三个正方形,面积分别为74英亩、116英亩、370英亩.三个正方形恰好围着一个池塘,如果有人能
计算出池塘的准确面积.则
池塘不计入土地价钱白白奉
送.英国数学家巴尔教授曾
经巧妙地解答了这个问题,
你能解决吗
新课精讲
探索新知
1
知识点
用勾股定理在数轴上表示数
我们知道数轴上的点有的表示有理数,有的表示无理
数,你能在数轴上画出表示 的点吗?
如果能画出长为 的线段,就能在数轴上画出表示
的点.容易知道,长为 的线段是两条直角边的长都
为1的直角三角形的斜边.长为 的线段能是直角边的长
为正整数的直角三角形的斜边吗?
探索新知
利用勾股定理,可以发现,直角边的长为正整数2, 3的直角三角形的斜边长为 .由此,可以依照如下方法在数轴上画出表示 的点.
如图,在数轴上找出表示3的点A, 则OA=3,过点A作直线l垂直于OA,在l上取点B,使AB = 2,以原点O为圆心,以OB为半径作弧,弧与数轴的交点C 即为表示 的点.
探索新知
总 结
类似地,利用勾股定理,可以作出长为
…的线段(图1).按照同样方法,可以在数轴上画出
表示 ……的点 (图 2).
图1
图2
探索新知
利用 a= 可以作出.
如图2,先作出与已知线段AB 垂直,
且与已知线段的端点A相交的直线l,
在直线l上以A为端点截取长为2a 的线
段AC,连接BC,则线段BC 即为所求.
如图2,BC就是所求作的线段.
例1 如图1,已知线段AB 的长为a,请作出长为 a 的
段.(保留作图痕迹,不写作法)
图1
图2
导引:
解:
探索新知
总 结
这类问题要作的线段一般是直角三角形的斜边,根据勾股定理由要作的线段确定两直角边的长是解题的关键.
典题精讲
1 在数轴上做出表示 的点.
如图所示.作法:
(1)在数轴上找出表示4的点A,则OA=4;
(2)过A作直线l 垂直于OA;
(3)在直线l上取点B,使AB=1;
(4)以原点O 为圆心,以OB 为半径作弧,弧与
数轴的交点C 即为表示 的点.
解:
典题精讲
2 如图,数轴上的点O,A,B 分别表示数0,1,2,过点B 作PQ⊥AB,以点B 为圆心,AB 的长为半径画弧,交PQ 于点C,以原点O 为圆心,OC 的长为半径画弧,交数轴于点M,则点M 表示的数是( )
A.
B.
C.
D.
B
典题精讲
3 如图,点C 表示的数是( )
A.1 B. C.1.5 D.
D
典题精讲
如图,在长方形ABCD 中,AB=3,AD=1,AB 在数轴上,若以点A为圆心,对角线AC 的长为半径作弧交数轴于点M,则点M 表示的数为( )
A.2
B. -1
C. -1
D.
4
C
探索新知
2
知识点
用勾股定理解几何问题
例2 如图,在△ABC 中,∠C=60°,AB=14,AC
=10. 求BC 的长.
导引:题中没有直角三角形,可以通
过作高构建直角三角形;过点
A作AD⊥BC 于D,图中会出现
两个直角三角形——Rt△ACD 和Rt△ABD,这两
个直角三角形有一条公共边AD,借助这条公共边,
可建立起直角三角形之间的联系.
探索新知
解:如图,过点A 作AD⊥BC 于D.
∵∠ADC=90°,∠C=60°,∴CD= AC=5.
在Rt△ACD中,
AD
在Rt△ABD中,
BD
∴BC=BD+CD=11+5=16.
探索新知
总 结
利用勾股定理求非直角三角形中线段的长的方法:
作三角形一边上的高,将其转化为两个直角三角形,然后利用勾股定理并结合已知条件,采用推理或列方程的方法解决问题.
典题精讲
1 如图,等边三角形的边长是6.求:
(1)高AD 的长;
(2)这个三角形的面积.
(1)由题意可知,在Rt△ADB 中,
AB=6,BD= BC=3,∠ADB=90°.
由勾股定理,
得AD=
(2)S△ABC= BC·AD= ×6×3
=
解:
典题精讲
如图是由4个边长为1的正方形构成的“田字格”,只用没有刻度的直尺在这个“田字格”中最多可以作出长度为 的线段________条.
2
8
典题精讲
如图,每个小正方形的边长均为1,则△ABC 中,长为无理
数的边有( )
A.0条
B.1条
C.2条
D.3条
C
典题精讲
4 如图是一张直角三角形的纸片,两直角边AC=6 cm,BC=8 cm,现将△ABC 折叠,使点B 与点A重合,折痕为DE,则BE 的长为( )
A.4 cm
B.5 cm
C.6 cm
D.10 cm
B
易错提醒
如图,把长方形纸条ABCD 沿EF,GH 同时折叠,B,C 两点恰好落在AD 边的P 点处,若∠FPH=90°,PF=8,PH=6,则长方形ABCD 的面积为________.
115.2
易错提醒
在Rt△PFH 中,FH=
=10,∴BC=BF+FH+CH=PF+FH+PH=8+10+6=24.设△PFH 的边FH 上的高为h,
则h= =4.8,
∴S长方形ABCD=24×4.8=115.2.
易错提醒
易错点:忽视题目中条件而求不出答案.
解此题时要灵活运用折叠前后对应线段相等,从而求出BC 的长,然后再运用面积法求出△PFH 中FH 边上的高,本题容易因忽视条件而求不出答案.
易错总结:
学以致用
小试牛刀
如图,在平面直角坐标系中,点P 的坐标为(-2,3),以点O 为圆心,以OP 的长为半径画弧,交x 轴的负半轴于点A,则点A 的横坐标介于( )
A.-4和-3之间
B.3和4之间
C.-5和-4之间
D.4和5之间
1
A
小试牛刀
如图,在矩形ABCD 中,BC=8,CD=6,将△ABE 沿BE 折叠,使点A恰好落在对角线BD上F 处,则DE 的长是( )
A.3
B.
C.5
D.
2
C
小试牛刀
如图,在等腰三角形ABC 中,AB=AC,BC 边上的高AD=6 cm,腰AB上的高CE=8 cm,则△ABC 的周长等于________cm.
3
小试牛刀
4 如图,正方形网格中的每个小正方形的边长都是1,
每个小格的顶点叫做格点.以格点为顶点画三角形.
(1)使三角形的三边长分别为 3,2 , .
(2)使三角形的周长为 .
小试牛刀
(1)如图①中的△ABC 为所求的三角形.
(2)如图②中的△ABC的三边长分别为 ,
三角形的周长为 .
解:
小试牛刀
如图,连接BD.因为AB=AD,∠A=60°,
所以∠1=∠ABD= =60°.
所以△ABD是等边三角形.所以BD=8.
又∠1+∠2=150°,则∠2=90°.
设BC=x,则CD=16-x,
由勾股定理得x 2=82+(16-x )2.
解得x=10.所以BC=10,CD=6.
5 如图,在四边形ABCD 中,AB=AD=8,
∠A=60°,∠D=150°,四边形的周长
为32,求BC 和CD 的长度.
解:
小试牛刀
6 [阅读理解]
如图,在△ABC中,BC=a,CA=b,AB=c.
(1)若∠C 为直角,则a 2+b 2=c 2;
(2)若∠C 为锐角,则a 2+b 2与c 2的关系为a 2+b 2>c 2;
(3)若∠C 为钝角,试推导a 2+b 2与c 2的关系.
[探究问题]在△ABC 中,BC=a=3,CA=b=4,
AB=c,若△ABC 是钝角三角形,求第三边c 的取值范围.
小试牛刀
[阅读理解](3)如图所示,作AD⊥BC 交BC 的延长线于D,则BD=BC+CD=a+CD,
在Rt△ABD 中,AD 2=AB 2-BD 2.
在Rt△ACD 中,AD 2=AC 2-CD 2,
∴AB 2-BD 2=AC 2-CD 2,
∴c 2-(a+CD )2=b 2-CD 2,
整理得a 2+b 2=c 2-2a ·CD.
∵a>0,CD>0,∴a 2+b 2<c 2;
解:
小试牛刀
[探究问题]当∠C 为钝角时, <c<a+b,
∵a=3,b=4,
∴ <c<3+4,即5<c<7;
当∠B 为钝角时,b-a<c< ,
∵a=3,b=4,
∴4-3<c< ,即1<c< .
综上所述第三边c的取值范围为5<c<7或1<c< .
小试牛刀
7 如图,在Rt△ABC中,∠C=90°,点D 是AB 的中点,点E,F 分别为AC,BC 的中点,DE⊥DF.求证:AE 2+BF 2=EF 2.
小试牛刀
如图,延长ED 至点G,使DG=ED,连接BG,FG.
在△ADE 和△BDG 中,
AD=DB,∠1=∠2,ED=DG,
∴△ADE ≌△BDG (SAS).
∴AE=BG,∠3=∠4.
又∵∠4+∠5=90°,∴∠3+∠5=90°.
又∵DF⊥EG,DE=DG,∴FG=EF.
在Rt△FBG 中,BG 2+BF 2=FG 2,
即AE 2+BF 2=EF 2.
证明:
课堂小结
课堂小结
1.勾股定理与三角形三边平方关系的综合应用:
单一应用:先由三角形三边平方关系得出直角三角形后,再求这个直角三角形的角度和面积:
综合应用:先用勾股定理求出三角形的边长,再由三角形平方关系确定三角形的形状,进而解决其他问题;
逆向应用:如果一个三角形两条较小边长的平方和不等于最大边长的平方,那么这个三角形就不是直角三角形.
课堂小结
2.应用勾股定理解题的方法:
(1)添线应用,即题中无直角三角形,可以通过作垂线,构
造直角三角形,应用勾股定理求解;
(2)借助方程应用,即题中虽有直角三角形,但已知线段的
长不完全是直角三角形的边长,可通过设未知数,构建
方程,解答计算问题;
(3)建模应用,即将实际问题建立直角三角形模型,通过勾
股定理解决实际问题.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
