【班海精品】人教版(新)八下-18.1 平行四边形 第三课时【优质课件】
文档属性
| 名称 | 【班海精品】人教版(新)八下-18.1 平行四边形 第三课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 6.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 10:20:43 | ||
图片预览









文档简介
(共57张PPT)
18.1 平行四边形
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
平行四边形的性质
平行四边形对边平行;
平行四边形对边相等;
平行四边形对角相等;
平行四边形对角线互相平分;
新课精讲
探索新知
1
知识点
由两组对边分别平行或相等判定平行四边形
一装潢店要招聘店员,老板出了这样一道考题:“一顾客要一张平行四边形的玻璃,你利用工具度量哪些数据可说明这张玻璃符合顾客要求.”
探索新知
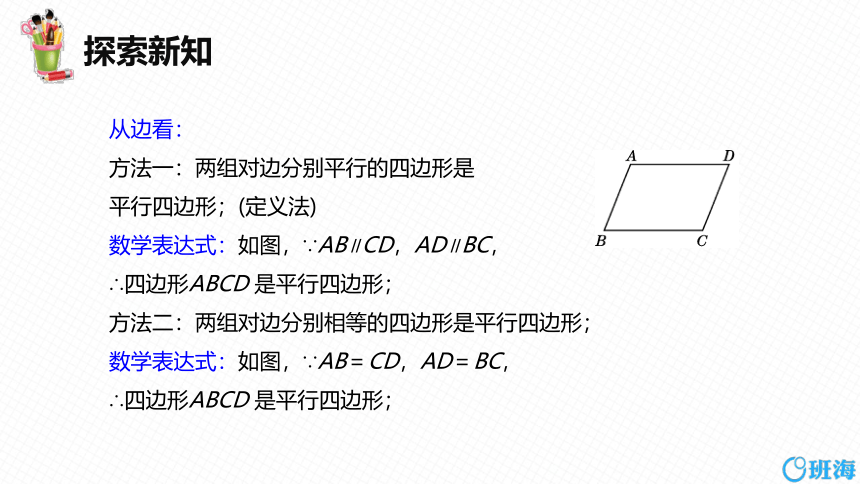
从边看:
方法一:两组对边分别平行的四边形是
平行四边形;(定义法)
数学表达式:如图,∵AB∥CD,AD∥BC,
∴四边形ABCD 是平行四边形;
方法二:两组对边分别相等的四边形是平行四边形;
数学表达式:如图,∵AB=CD,AD=BC,
∴四边形ABCD 是平行四边形;
探索新知
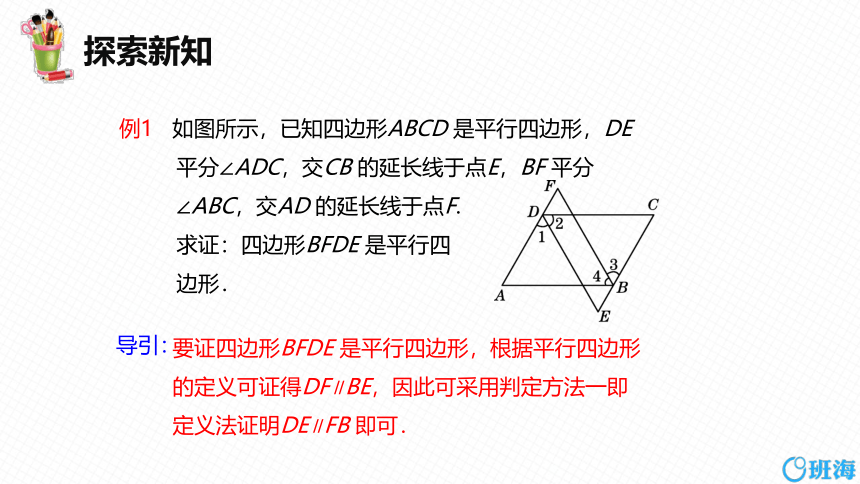
要证四边形BFDE 是平行四边形,根据平行四边形的定义可证得DF∥BE,因此可采用判定方法一即定义法证明DE∥FB 即可.
例1 如图所示,已知四边形ABCD 是平行四边形,DE
平分∠ADC,交CB 的延长线于点E,BF 平分
∠ABC,交AD 的延长线于点F.
求证:四边形BFDE 是平行四
边形.
导引:
探索新知
∵四边形ABCD 是平行四边形,
∴∠ADC=∠ABC,AD∥CB. ∴DF∥BE.
∵DE 平分∠ADC,BF 平分∠ABC,
∴∠1=∠2=∠3=∠4.
∵AD∥BC,∴∠1=∠E. ∴∠E=∠3.
∴DE∥FB.
∴四边形BFDE 是平行四边形.(两组对边分别平行
的四边形是平行四边形)
证明:
探索新知
总 结
平行四边形的定义是判定平行四边形的根本方法,也是其他判定方法的基础.当题目中出现平行的线段时,往往借助判定方法一来帮助我们对四边形加以判断.
探索新知
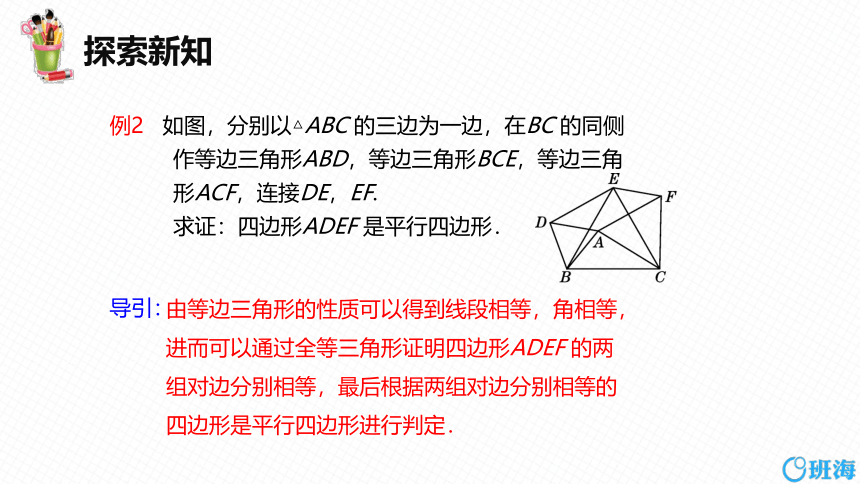
例2 如图,分别以△ABC 的三边为一边,在BC 的同侧
作等边三角形ABD,等边三角形BCE,等边三角
形ACF,连接DE,EF.
求证:四边形ADEF 是平行四边形.
由等边三角形的性质可以得到线段相等,角相等,进而可以通过全等三角形证明四边形ADEF 的两组对边分别相等,最后根据两组对边分别相等的四边形是平行四边形进行判定.
导引:
探索新知
∵△ABD、△BCE、△ACF 都为等边三角形,
∴DB=AB=AD,BE=BC,AC=AF,
∠DBA=60°,∠EBC=60°.
∴∠DBE=60°-∠EBA,∠ABC=60°-∠EBA,
∴∠DBE=∠ABC,∴△DBE ≌ △ABC,
∴DE=AC.
又∵AC=AF,∴AF=DE.
同理可证:△ABC ≌ △FEC,
∴AB=FE,∴FE=AD,
∴四边形ADEF 是平行四边形.
证明:
探索新知
总 结
根据等边三角形的性质可以得到线段相等,角相等,进而通过证明三角形全等得到四边形ADEF 的两组对边分别相等,根据两组对边分别相等的四边形是平行四边形得证.
典题精讲
如图,AB=DC=EF,AD=BC,DE=CF. 图中有哪些互相平行的线段?
1
AB∥CD,AD∥BC,
CD∥EF,DE∥CF,
AB∥EF.
解:
典题精讲
2 四边形的四条边长分别是a,b,c,d,其中a,b 为
一组对边长,c,d 为另一组对边长且a 2+b 2+c 2+d 2
=2ab+2cd,则这个四边形是( )
A.任意四边形
B.平行四边形
C.对角线相等的四边形
D.对角线垂直的四边形
B
探索新知
2
知识点
由两组对角分别相等判定平行四边形
几何语言:
∵∠ABC=∠ADC,∠BAD=∠BCD,
∴四边形ABCD 是平行四边形.(如图所示)
探索新知
例3 如图,在 ABCD 中,BE 平分∠ABC,交AD 于点E,DF
平分∠ADC,交BC 于点F,那么四边形BFDE 是平行四边
形吗?为什么?
利用平行四边形对角相等
的性质可得∠ABC=
∠ADC,∠A=∠C,然后
再依据角平分线的定
义和三角形外角的性质证出四边形BFDE 的两组对角分别相等,于是可得出结论.
导引:
探索新知
四边形BFDE 是平行四边形.
理由:在 ABCD 中,∠ABC=∠ADC,∠A=∠C.
∵BE平分∠ABC,DF 平分∠ADC,
∴∠ABE=∠CBE= ∠ABC,
∠CDF=∠ADF= ∠ADC,
∴∠CDF=∠ADF=∠ABE=∠CBE.
∵∠DFB=∠C+∠CDF,∠BED=∠ABE+∠A,
∴∠DFB=∠BED,∴四边形BFDE 是平行四边形.
解:
探索新知
总 结
当已知条件出现所要说明的四边形的角时,可选择“两组对角分别相等的四边形是平行四边形”来判定.
典题精讲
下列条件不能判定四边形ABCD 是平行四边形的是( )
A.∠A=∠C,∠B=∠D
B.∠A=∠B=∠C=90°
C.∠A+∠B=180°,∠B+∠C=180°
D.∠A+∠B=180°,∠C+∠D=180°
1
D
典题精讲
2 下列给出的条件中,能判定四边形ABCD 是平行四边形的是( )
A.AB∥CD,AD=BC
B.AB=AD,CB=CD
C.AB=CD,AD=BC
D.∠B=∠C,∠A=∠D
C
探索新知
3
知识点
由对角线互相平分判定平行四边形
过前面的学习,我们知道,平行四边形的对边相等、对角相等、对角线互相平分.反过来,对边相等,或对角相等,或对角线互相平分的四边形是平行四边形吗?也就是说,平行四边形的性质定理的逆命题成立吗?
下面我们以“对角线互相平分的四边形是平行四边形”为例,通过三角形全等进行证明.
思考
探索新知
如图,在四边形ABCD 中,AC,BD 相交于点O,且OA=OC,OB=OD.
求证:四边形ABCD是平行四边形.
∵OA=OC,OD=OB,
∠AOD=∠COB,
∴△ AOD ≌ △COB.
∴∠OAD=∠OCB.
∴AD//BC.
同理 AB//DC.
∴四边形ABCD 是平行四边形.
证明:
探索新知
从对角线看:
对角线互相平分的四边形是平行四边形.
数学表达式:如图,∵OA=OC,OB=OD,
∴四边形ABCD 是平行四边形.
探索新知
∵ 四边形ABCD 是平行四边形,
∴ AO=CO,BO=DO.
∵ AE=CF,
∴AO-AE=CO-CF,即EO=FO.
又 BO=DO,
∴四边形BFDE 是平行四边形.
例4 如图, ABCD 的对角线AC,BD 相交于点O,
E,F 是AC上的两点,并且AE=CF.
求证:四边形BFDE 是平行四边形.
证明:
探索新知
总 结
从对角线方面判断四边形的形状要注意是对角线互相平分,即交点既是第一条对角线的中点,又是第二条对角线的中点.
典题精讲
如图, ABCD 的对角线AC,BD 相交于点O,E,F 分别是OA,OC 的中点. 求证BE=DF.
1
因为四边形ABCD 是平行四边形,
所以BO=DO,OA=OC.
因为E,F 分别是OA,OC 的中点,
所以OE= OA= OC=OF.
又因为∠BOE=∠DOF,
所以△BOE ≌ △DOF,所以BE=DF.
解:
典题精讲
如图,四边形ABCD 的对角线相交于点O,AO=CO,请添加一个条件__________(只添一个即可),使四边形ABCD 是平行四边形.
2
BO=DO
探索新知
4
知识点
由一组对边平行且相等判定平行四边形
我们知道,如果一个四边形是平行四边形,那么它的任意一组对边平行且相等.反过来,一组对边平行且相等的四边形是平行四边形吗?我们猜想这个结论正确,下面进行证明.
思考
探索新知
如图,在四边形ABCD 中, AB//CD,且AB=CD.
求证:四边形ABCD 是平行四边形.
连接AC,
∵AB//CD,
∴∠1=∠2.
又AB=CD,AC=CA.
∴△ ABC ≌ △CDA.
∴BC=DA.
∴四边形ABCD 两组对边分别相等,它是平行四边形.
证明:
探索新知
归 纳
于是我们又得到平行四边形的一个判断定理:
一组对边平行且相等的四边形是平行四边形.
一组对边平行且相等的四边形是平行四边形;
数学表达式:如图,∵AB CD,
∴四边形ABCD是平行四边形.
∥
=
探索新知
∵四边形ABCD 是平行四边形,
∴ AB=CD,EB//FD.
又EB= AB,FD = CD,
∴ EB=FD.
∴四边形EBFD 是平行四边形.
例5 如图,在 ABCD 中,E,F 分别是AB,CD 的中点.
求证:四边形EBFD 是平行四边形.
证明:
探索新知
总 结
要证四边形是平行四边形,已知有一组对边平行,联想的思路有两种:
一是证明另一组对边平行;
二是证明平行的这组对边相等.
而证明边相等要三角形全等这条思路较常见.
典题精讲
为了保证铁路的两条直铺的铁轨互相平行,只要使互相平行的夹在铁轨之间的枕木长相等就可以了. 你能说出其中的道理吗?
1
因为一组对边平行
且相等的四边形是
平行四边形,所以
铁轨和夹在铁轨之间的枕木构成了平行四边形,因此可知两条直铺的铁轨是互相平行的.
解:
典题精讲
如图,在 ABCD 中,BD 是它的一条对角线,过A,C 两点分别作AE丄BD, CF丄BD,E,F 为垂足. 求证:四边形AFGE 是平行四边形.
2
典题精讲
因为四边形ABCD 是平行四边形,
所以AB∥CD,AB=CD,所以∠CDB=∠ABD.
又因为AE⊥BD,CF⊥BD,
所以∠AEB=∠CFD=90°,所以AE∥CF.
在△ABE 和△CDF 中,
AB=CD,∠ABE=∠CDF,∠AEB=∠CFD,
所以△ABE ≌ △CDF,所以AE=CF.
又因为AE∥CF,所以四边形AFCE 是平行四边形.
解:
典题精讲
3 下列说法错误的是( )
A.对角线互相平分的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边相等,另一组对边平行的四边形是平行四边形
D
4
下列条件不能判定四边形ABCD 是平行四边形的是( )
A.AB∥CD,AD∥BC
B.∠A=∠C,∠B=∠D
C.AB=CD,AD=BC
D.AB∥CD,AD=BC
D
易错提醒
已知:如图,在 ABCD 中,对角线AC,BD 相交于O,E,F 是对角线上的两点,给出下列四个条
件:①OE=OF;②DE=BF;③∠ADE=
∠CBF;④∠ABE=∠CDF.
其中不能判定四边形DEBF 是平行四边形的有( )
A.0个 B.1个 C.2个 D.3个
B
易错点:混淆平行四边形的判定方法导致判断错误.
易错提醒
给出条件①OE=OF,由题易知OD=OB,∴四边形DEBF 为平行四边形,故①正确;给出条件③∠ADE=∠CBF,由题易知∠DAE=∠BCF,AD=BC,∴△ADE ≌ △CBF,∴DE=BF,∠DEA=∠BFC,∴∠DEO=∠BFO,∴DE∥BF,∴四边形DEBF为平行四边形,故③正确;给出条件④,理由同③,亦可判定四边形DEBF 为平行四边形;只有给出条件②无法判定四边形DEBF 为平行四边形.故选B. 本题易错选A.
学以致用
小试牛刀
小敏不慎将一块平行四边形玻璃打碎成如图所示的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,她带了两块碎玻璃,其编号应该是( )
A.①②
B.①④
C.③④
D.②③
1
D
小试牛刀
如图,线段AB,CD 相交于点O,且图上各点把线段AB,CD四等分,这些点可以构成________个平行四边形.
2
4
小试牛刀
3
如图,在四边形ABCD 中,AB∥CD,要使四边形ABCD 是平行四边形,可添加的条件不正确的是( )
A.AB=CD
B.BC=AD
C.∠A=∠C
D.BC∥AD
B
小试牛刀
4
如图,在 ABCD 中,点E,F 分别在AD,BC上,若要使四边形AFCE 是平行四边形,可以添加的条件是( )
①AF=CF;②AE=CE;③BF=DE;④AF∥CE.
A.①或②
B.②或③
C.③或④
D.①或③
C
小试牛刀
如图,点B,E 分别在AC,DF 上,AF 分别交BD,CE
于点M,N,∠A=∠F,∠1=∠2.
(1)求证:四边形BCED 是平行四边形;
(2)已知DE=2,连接BN,若BN 平分∠DBC,求CN 的长.
小试牛刀
(1)证明:∵∠A=∠F,∴DF∥AC.
又∵∠1=∠2,∠1=∠DMF,
∴∠2=∠DMF. ∴DB∥EC.
∴四边形BCED是平行四边形.
(2)解:∵BN 平分∠DBC,
∴∠DBN=∠NBC.
∵DB∥EC,∴∠BNC=∠DBN.
∴∠BNC=∠NBC. ∴BC=CN.
∵四边形BCED 是平行四边形,
∴BC=DE=2. ∴CN=2.
小试牛刀
如图,在 ABCD 中,点E,F 在对角线AC上,
且AE=CF. 求证:
(1)DE=BF;
(2)四边形DEBF 是平行四边形.
小试牛刀
(1)∵四边形ABCD 是平行四边形.
∴AD∥CB,AD=CB. ∴∠DAE=∠BCF.
在△ADE 和△CBF 中,
∴△ADE ≌ △CBF. ∴DE=BF.
(2)如图,连接BD,交AC 于点O,
∵四边形ABCD 是平行四边形,
∴OA=OC,OB=OD.
∵AE=CF,∴OE=OF.
∴四边形DEBF 是平行四边形.
证明:
小试牛刀
如图,以BC 为底边的等腰△ABC,点D,E,G 分别在BC,
AB,AC上,且EG∥BC,DE∥AC,延长GE 至点F,使得BF=BE.
(1)求证:四边形BDEF 为平行四边形;
(2)当∠C=45°,BD=2时,求D,F 两点间的距离.
小试牛刀
(1) ∵△ABC 是等腰三角形,
∴∠ABC=∠C.
∵EG∥BC,DE∥AC,
∴∠AEG=∠ABC=∠C,
四边形CDEG 是平行四边形.
∴∠DEG=∠C.
∵BE=BF,
∴∠BEF=∠F=∠AEG=∠ABC.
∴∠F=∠DEG. ∴BF∥DE.
∴四边形BDEF 为平行四边形.
证明:
小试牛刀
(2)∵∠C=45°,
∴∠BDE=∠ABC=∠BEF=∠BFE=45°.
∴△BDE、△BEF 是等腰直角三角形.
∵BD=2,∴BF=BE= .
作FM⊥BD 交DB 的延长线于M,连接DF,
如图所示.
易得△BFM 是等腰直角三角形,
∴FM=BM=1.∴DM=3.
在Rt△DFM 中,
由勾股定理得DF= ,
即D,F 两点间的距离为 .
解:
小试牛刀
如图,已知点E,C 在线段BF 上,BE=EC=CF,
AB∥DE,∠ACB=∠F.
(1)求证:△ABC ≌ △DEF;
(2)试判断四边形AECD 的形状,并证明你的结论.
小试牛刀
(1) ∵AB∥DE,
∴∠B=∠DEF.
∵BE=EC=CF,∴BC=EF.
在△ABC 和△DEF 中,
∴△ABC ≌ △DEF.
证明:
小试牛刀
(2) 四边形AECD 是平行四边形.
证明:∵△ABC ≌ △DEF,
∴AC=DF.
∵∠ACB=∠F,∴AC∥DF.
∴四边形ACFD 是平行四边形.
∴AD∥CF,AD=CF.
∵EC=CF,∴AD=EC.
又∵AD∥EC,
∴四边形AECD 是平行四边形.
解:
课堂小结
课堂小结
平行四边形的判定方法:
(1)定义:两组对边分别平行的四边形是平行四边形.
(2)两组对边分别相等的四边形是平行四边形.
(3)对角线互相平分的四边形是平行四边形.
(4)两组对角分别相等的四边形是平行四边形.
(5)一组对边平行且相等的四边形是平行四边形.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
18.1 平行四边形
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
平行四边形的性质
平行四边形对边平行;
平行四边形对边相等;
平行四边形对角相等;
平行四边形对角线互相平分;
新课精讲
探索新知
1
知识点
由两组对边分别平行或相等判定平行四边形
一装潢店要招聘店员,老板出了这样一道考题:“一顾客要一张平行四边形的玻璃,你利用工具度量哪些数据可说明这张玻璃符合顾客要求.”
探索新知
从边看:
方法一:两组对边分别平行的四边形是
平行四边形;(定义法)
数学表达式:如图,∵AB∥CD,AD∥BC,
∴四边形ABCD 是平行四边形;
方法二:两组对边分别相等的四边形是平行四边形;
数学表达式:如图,∵AB=CD,AD=BC,
∴四边形ABCD 是平行四边形;
探索新知
要证四边形BFDE 是平行四边形,根据平行四边形的定义可证得DF∥BE,因此可采用判定方法一即定义法证明DE∥FB 即可.
例1 如图所示,已知四边形ABCD 是平行四边形,DE
平分∠ADC,交CB 的延长线于点E,BF 平分
∠ABC,交AD 的延长线于点F.
求证:四边形BFDE 是平行四
边形.
导引:
探索新知
∵四边形ABCD 是平行四边形,
∴∠ADC=∠ABC,AD∥CB. ∴DF∥BE.
∵DE 平分∠ADC,BF 平分∠ABC,
∴∠1=∠2=∠3=∠4.
∵AD∥BC,∴∠1=∠E. ∴∠E=∠3.
∴DE∥FB.
∴四边形BFDE 是平行四边形.(两组对边分别平行
的四边形是平行四边形)
证明:
探索新知
总 结
平行四边形的定义是判定平行四边形的根本方法,也是其他判定方法的基础.当题目中出现平行的线段时,往往借助判定方法一来帮助我们对四边形加以判断.
探索新知
例2 如图,分别以△ABC 的三边为一边,在BC 的同侧
作等边三角形ABD,等边三角形BCE,等边三角
形ACF,连接DE,EF.
求证:四边形ADEF 是平行四边形.
由等边三角形的性质可以得到线段相等,角相等,进而可以通过全等三角形证明四边形ADEF 的两组对边分别相等,最后根据两组对边分别相等的四边形是平行四边形进行判定.
导引:
探索新知
∵△ABD、△BCE、△ACF 都为等边三角形,
∴DB=AB=AD,BE=BC,AC=AF,
∠DBA=60°,∠EBC=60°.
∴∠DBE=60°-∠EBA,∠ABC=60°-∠EBA,
∴∠DBE=∠ABC,∴△DBE ≌ △ABC,
∴DE=AC.
又∵AC=AF,∴AF=DE.
同理可证:△ABC ≌ △FEC,
∴AB=FE,∴FE=AD,
∴四边形ADEF 是平行四边形.
证明:
探索新知
总 结
根据等边三角形的性质可以得到线段相等,角相等,进而通过证明三角形全等得到四边形ADEF 的两组对边分别相等,根据两组对边分别相等的四边形是平行四边形得证.
典题精讲
如图,AB=DC=EF,AD=BC,DE=CF. 图中有哪些互相平行的线段?
1
AB∥CD,AD∥BC,
CD∥EF,DE∥CF,
AB∥EF.
解:
典题精讲
2 四边形的四条边长分别是a,b,c,d,其中a,b 为
一组对边长,c,d 为另一组对边长且a 2+b 2+c 2+d 2
=2ab+2cd,则这个四边形是( )
A.任意四边形
B.平行四边形
C.对角线相等的四边形
D.对角线垂直的四边形
B
探索新知
2
知识点
由两组对角分别相等判定平行四边形
几何语言:
∵∠ABC=∠ADC,∠BAD=∠BCD,
∴四边形ABCD 是平行四边形.(如图所示)
探索新知
例3 如图,在 ABCD 中,BE 平分∠ABC,交AD 于点E,DF
平分∠ADC,交BC 于点F,那么四边形BFDE 是平行四边
形吗?为什么?
利用平行四边形对角相等
的性质可得∠ABC=
∠ADC,∠A=∠C,然后
再依据角平分线的定
义和三角形外角的性质证出四边形BFDE 的两组对角分别相等,于是可得出结论.
导引:
探索新知
四边形BFDE 是平行四边形.
理由:在 ABCD 中,∠ABC=∠ADC,∠A=∠C.
∵BE平分∠ABC,DF 平分∠ADC,
∴∠ABE=∠CBE= ∠ABC,
∠CDF=∠ADF= ∠ADC,
∴∠CDF=∠ADF=∠ABE=∠CBE.
∵∠DFB=∠C+∠CDF,∠BED=∠ABE+∠A,
∴∠DFB=∠BED,∴四边形BFDE 是平行四边形.
解:
探索新知
总 结
当已知条件出现所要说明的四边形的角时,可选择“两组对角分别相等的四边形是平行四边形”来判定.
典题精讲
下列条件不能判定四边形ABCD 是平行四边形的是( )
A.∠A=∠C,∠B=∠D
B.∠A=∠B=∠C=90°
C.∠A+∠B=180°,∠B+∠C=180°
D.∠A+∠B=180°,∠C+∠D=180°
1
D
典题精讲
2 下列给出的条件中,能判定四边形ABCD 是平行四边形的是( )
A.AB∥CD,AD=BC
B.AB=AD,CB=CD
C.AB=CD,AD=BC
D.∠B=∠C,∠A=∠D
C
探索新知
3
知识点
由对角线互相平分判定平行四边形
过前面的学习,我们知道,平行四边形的对边相等、对角相等、对角线互相平分.反过来,对边相等,或对角相等,或对角线互相平分的四边形是平行四边形吗?也就是说,平行四边形的性质定理的逆命题成立吗?
下面我们以“对角线互相平分的四边形是平行四边形”为例,通过三角形全等进行证明.
思考
探索新知
如图,在四边形ABCD 中,AC,BD 相交于点O,且OA=OC,OB=OD.
求证:四边形ABCD是平行四边形.
∵OA=OC,OD=OB,
∠AOD=∠COB,
∴△ AOD ≌ △COB.
∴∠OAD=∠OCB.
∴AD//BC.
同理 AB//DC.
∴四边形ABCD 是平行四边形.
证明:
探索新知
从对角线看:
对角线互相平分的四边形是平行四边形.
数学表达式:如图,∵OA=OC,OB=OD,
∴四边形ABCD 是平行四边形.
探索新知
∵ 四边形ABCD 是平行四边形,
∴ AO=CO,BO=DO.
∵ AE=CF,
∴AO-AE=CO-CF,即EO=FO.
又 BO=DO,
∴四边形BFDE 是平行四边形.
例4 如图, ABCD 的对角线AC,BD 相交于点O,
E,F 是AC上的两点,并且AE=CF.
求证:四边形BFDE 是平行四边形.
证明:
探索新知
总 结
从对角线方面判断四边形的形状要注意是对角线互相平分,即交点既是第一条对角线的中点,又是第二条对角线的中点.
典题精讲
如图, ABCD 的对角线AC,BD 相交于点O,E,F 分别是OA,OC 的中点. 求证BE=DF.
1
因为四边形ABCD 是平行四边形,
所以BO=DO,OA=OC.
因为E,F 分别是OA,OC 的中点,
所以OE= OA= OC=OF.
又因为∠BOE=∠DOF,
所以△BOE ≌ △DOF,所以BE=DF.
解:
典题精讲
如图,四边形ABCD 的对角线相交于点O,AO=CO,请添加一个条件__________(只添一个即可),使四边形ABCD 是平行四边形.
2
BO=DO
探索新知
4
知识点
由一组对边平行且相等判定平行四边形
我们知道,如果一个四边形是平行四边形,那么它的任意一组对边平行且相等.反过来,一组对边平行且相等的四边形是平行四边形吗?我们猜想这个结论正确,下面进行证明.
思考
探索新知
如图,在四边形ABCD 中, AB//CD,且AB=CD.
求证:四边形ABCD 是平行四边形.
连接AC,
∵AB//CD,
∴∠1=∠2.
又AB=CD,AC=CA.
∴△ ABC ≌ △CDA.
∴BC=DA.
∴四边形ABCD 两组对边分别相等,它是平行四边形.
证明:
探索新知
归 纳
于是我们又得到平行四边形的一个判断定理:
一组对边平行且相等的四边形是平行四边形.
一组对边平行且相等的四边形是平行四边形;
数学表达式:如图,∵AB CD,
∴四边形ABCD是平行四边形.
∥
=
探索新知
∵四边形ABCD 是平行四边形,
∴ AB=CD,EB//FD.
又EB= AB,FD = CD,
∴ EB=FD.
∴四边形EBFD 是平行四边形.
例5 如图,在 ABCD 中,E,F 分别是AB,CD 的中点.
求证:四边形EBFD 是平行四边形.
证明:
探索新知
总 结
要证四边形是平行四边形,已知有一组对边平行,联想的思路有两种:
一是证明另一组对边平行;
二是证明平行的这组对边相等.
而证明边相等要三角形全等这条思路较常见.
典题精讲
为了保证铁路的两条直铺的铁轨互相平行,只要使互相平行的夹在铁轨之间的枕木长相等就可以了. 你能说出其中的道理吗?
1
因为一组对边平行
且相等的四边形是
平行四边形,所以
铁轨和夹在铁轨之间的枕木构成了平行四边形,因此可知两条直铺的铁轨是互相平行的.
解:
典题精讲
如图,在 ABCD 中,BD 是它的一条对角线,过A,C 两点分别作AE丄BD, CF丄BD,E,F 为垂足. 求证:四边形AFGE 是平行四边形.
2
典题精讲
因为四边形ABCD 是平行四边形,
所以AB∥CD,AB=CD,所以∠CDB=∠ABD.
又因为AE⊥BD,CF⊥BD,
所以∠AEB=∠CFD=90°,所以AE∥CF.
在△ABE 和△CDF 中,
AB=CD,∠ABE=∠CDF,∠AEB=∠CFD,
所以△ABE ≌ △CDF,所以AE=CF.
又因为AE∥CF,所以四边形AFCE 是平行四边形.
解:
典题精讲
3 下列说法错误的是( )
A.对角线互相平分的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边相等,另一组对边平行的四边形是平行四边形
D
4
下列条件不能判定四边形ABCD 是平行四边形的是( )
A.AB∥CD,AD∥BC
B.∠A=∠C,∠B=∠D
C.AB=CD,AD=BC
D.AB∥CD,AD=BC
D
易错提醒
已知:如图,在 ABCD 中,对角线AC,BD 相交于O,E,F 是对角线上的两点,给出下列四个条
件:①OE=OF;②DE=BF;③∠ADE=
∠CBF;④∠ABE=∠CDF.
其中不能判定四边形DEBF 是平行四边形的有( )
A.0个 B.1个 C.2个 D.3个
B
易错点:混淆平行四边形的判定方法导致判断错误.
易错提醒
给出条件①OE=OF,由题易知OD=OB,∴四边形DEBF 为平行四边形,故①正确;给出条件③∠ADE=∠CBF,由题易知∠DAE=∠BCF,AD=BC,∴△ADE ≌ △CBF,∴DE=BF,∠DEA=∠BFC,∴∠DEO=∠BFO,∴DE∥BF,∴四边形DEBF为平行四边形,故③正确;给出条件④,理由同③,亦可判定四边形DEBF 为平行四边形;只有给出条件②无法判定四边形DEBF 为平行四边形.故选B. 本题易错选A.
学以致用
小试牛刀
小敏不慎将一块平行四边形玻璃打碎成如图所示的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,她带了两块碎玻璃,其编号应该是( )
A.①②
B.①④
C.③④
D.②③
1
D
小试牛刀
如图,线段AB,CD 相交于点O,且图上各点把线段AB,CD四等分,这些点可以构成________个平行四边形.
2
4
小试牛刀
3
如图,在四边形ABCD 中,AB∥CD,要使四边形ABCD 是平行四边形,可添加的条件不正确的是( )
A.AB=CD
B.BC=AD
C.∠A=∠C
D.BC∥AD
B
小试牛刀
4
如图,在 ABCD 中,点E,F 分别在AD,BC上,若要使四边形AFCE 是平行四边形,可以添加的条件是( )
①AF=CF;②AE=CE;③BF=DE;④AF∥CE.
A.①或②
B.②或③
C.③或④
D.①或③
C
小试牛刀
如图,点B,E 分别在AC,DF 上,AF 分别交BD,CE
于点M,N,∠A=∠F,∠1=∠2.
(1)求证:四边形BCED 是平行四边形;
(2)已知DE=2,连接BN,若BN 平分∠DBC,求CN 的长.
小试牛刀
(1)证明:∵∠A=∠F,∴DF∥AC.
又∵∠1=∠2,∠1=∠DMF,
∴∠2=∠DMF. ∴DB∥EC.
∴四边形BCED是平行四边形.
(2)解:∵BN 平分∠DBC,
∴∠DBN=∠NBC.
∵DB∥EC,∴∠BNC=∠DBN.
∴∠BNC=∠NBC. ∴BC=CN.
∵四边形BCED 是平行四边形,
∴BC=DE=2. ∴CN=2.
小试牛刀
如图,在 ABCD 中,点E,F 在对角线AC上,
且AE=CF. 求证:
(1)DE=BF;
(2)四边形DEBF 是平行四边形.
小试牛刀
(1)∵四边形ABCD 是平行四边形.
∴AD∥CB,AD=CB. ∴∠DAE=∠BCF.
在△ADE 和△CBF 中,
∴△ADE ≌ △CBF. ∴DE=BF.
(2)如图,连接BD,交AC 于点O,
∵四边形ABCD 是平行四边形,
∴OA=OC,OB=OD.
∵AE=CF,∴OE=OF.
∴四边形DEBF 是平行四边形.
证明:
小试牛刀
如图,以BC 为底边的等腰△ABC,点D,E,G 分别在BC,
AB,AC上,且EG∥BC,DE∥AC,延长GE 至点F,使得BF=BE.
(1)求证:四边形BDEF 为平行四边形;
(2)当∠C=45°,BD=2时,求D,F 两点间的距离.
小试牛刀
(1) ∵△ABC 是等腰三角形,
∴∠ABC=∠C.
∵EG∥BC,DE∥AC,
∴∠AEG=∠ABC=∠C,
四边形CDEG 是平行四边形.
∴∠DEG=∠C.
∵BE=BF,
∴∠BEF=∠F=∠AEG=∠ABC.
∴∠F=∠DEG. ∴BF∥DE.
∴四边形BDEF 为平行四边形.
证明:
小试牛刀
(2)∵∠C=45°,
∴∠BDE=∠ABC=∠BEF=∠BFE=45°.
∴△BDE、△BEF 是等腰直角三角形.
∵BD=2,∴BF=BE= .
作FM⊥BD 交DB 的延长线于M,连接DF,
如图所示.
易得△BFM 是等腰直角三角形,
∴FM=BM=1.∴DM=3.
在Rt△DFM 中,
由勾股定理得DF= ,
即D,F 两点间的距离为 .
解:
小试牛刀
如图,已知点E,C 在线段BF 上,BE=EC=CF,
AB∥DE,∠ACB=∠F.
(1)求证:△ABC ≌ △DEF;
(2)试判断四边形AECD 的形状,并证明你的结论.
小试牛刀
(1) ∵AB∥DE,
∴∠B=∠DEF.
∵BE=EC=CF,∴BC=EF.
在△ABC 和△DEF 中,
∴△ABC ≌ △DEF.
证明:
小试牛刀
(2) 四边形AECD 是平行四边形.
证明:∵△ABC ≌ △DEF,
∴AC=DF.
∵∠ACB=∠F,∴AC∥DF.
∴四边形ACFD 是平行四边形.
∴AD∥CF,AD=CF.
∵EC=CF,∴AD=EC.
又∵AD∥EC,
∴四边形AECD 是平行四边形.
解:
课堂小结
课堂小结
平行四边形的判定方法:
(1)定义:两组对边分别平行的四边形是平行四边形.
(2)两组对边分别相等的四边形是平行四边形.
(3)对角线互相平分的四边形是平行四边形.
(4)两组对角分别相等的四边形是平行四边形.
(5)一组对边平行且相等的四边形是平行四边形.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
