【班海精品】人教版(新)八下-18.2 特殊的平行四边形 第一课时【优质课件】
文档属性
| 名称 | 【班海精品】人教版(新)八下-18.2 特殊的平行四边形 第一课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 5.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 10:20:43 | ||
图片预览






文档简介
(共49张PPT)
18.2 特殊的平行四边形
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
1.什么叫平行四边形?
3.平行四边形有哪些性质?
①平行四边形的对角相等.
②平行四边形的对边相等.
③平行四边形的对角线互相平分.
2.平行四边形与四边形
有什么关系?
A
B
C
D
两组对边分别平行的四边形叫做平行四边形 .
特殊
一般
平行四边形
具有四边形的
一切性质
新课精讲
探索新知
1
知识点
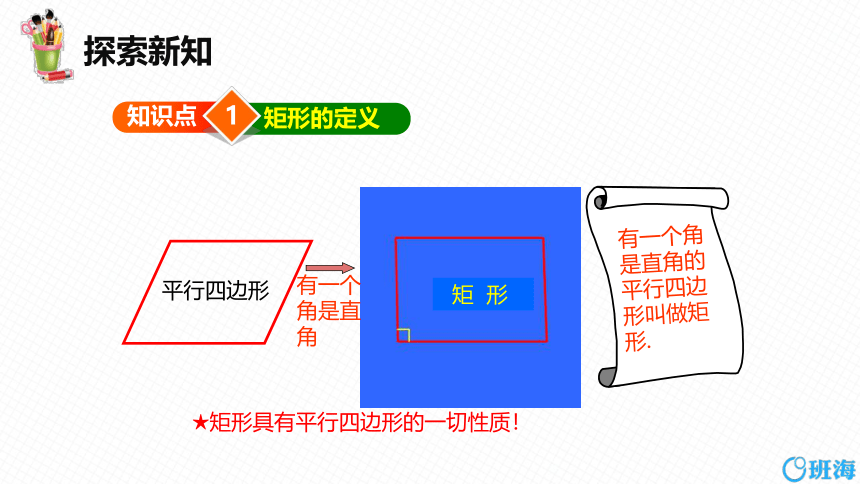
矩形的定义
平行四边形
长方形
有一个角是直角
矩 形
有一个角是直角的平行四边形叫做矩形.
★矩形具有平行四边形的一切性质!
探索新知
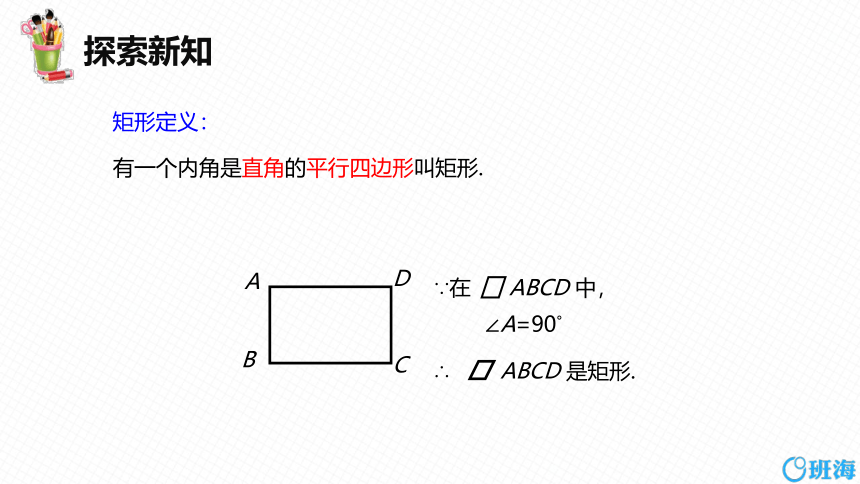
有一个内角是直角的平行四边形叫矩形.
矩形定义:
A
B
C
D
∵在 ABCD 中,
∠A=90°
∴ ABCD 是矩形.
探索新知
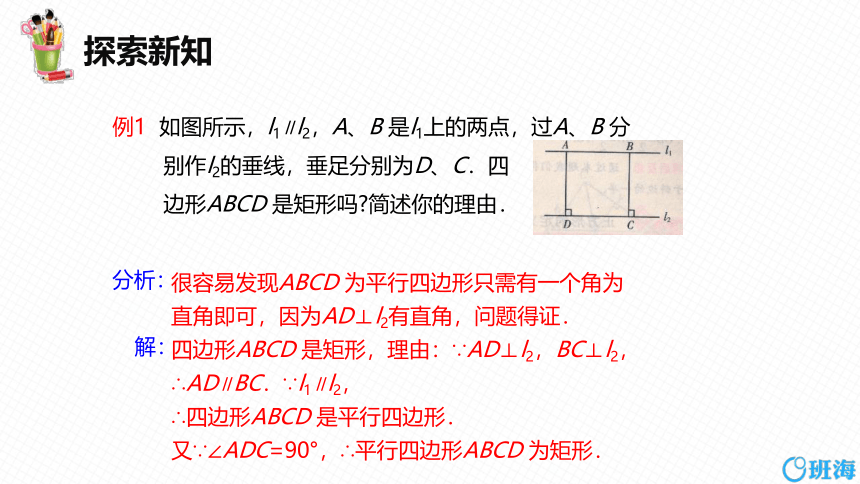
例1 如图所示,l1∥l2,A、B 是l1上的两点,过A、B 分
别作l2的垂线,垂足分别为D、C.四
边形ABCD 是矩形吗 简述你的理由.
很容易发现ABCD 为平行四边形只需有一个角为
直角即可,因为AD⊥l2有直角,问题得证.
四边形ABCD 是矩形,理由:∵AD⊥l2,BC⊥l2,
∴AD∥BC.∵l1∥l2,
∴四边形ABCD 是平行四边形.
又∵∠ADC=90°,∴平行四边形ABCD 为矩形.
分析:
解:
探索新知
总 结
利用定义识别一个四边形是矩形,首先要证明四边形是平行四边形,然后证明平行四边形有一个角是直角.
典题精讲
1
矩形是轴对称图形吗?如果是,它有几条对称轴?
是,它有2条对称轴.
解:
2
下列说法不正确的是( )
A.矩形是平行四边形
B.矩形不一定是平行四边形
C.有一个角是直角的平行四边形是矩形
D.平行四边形具有的性质矩形都具有
B
探索新知
2
知识点
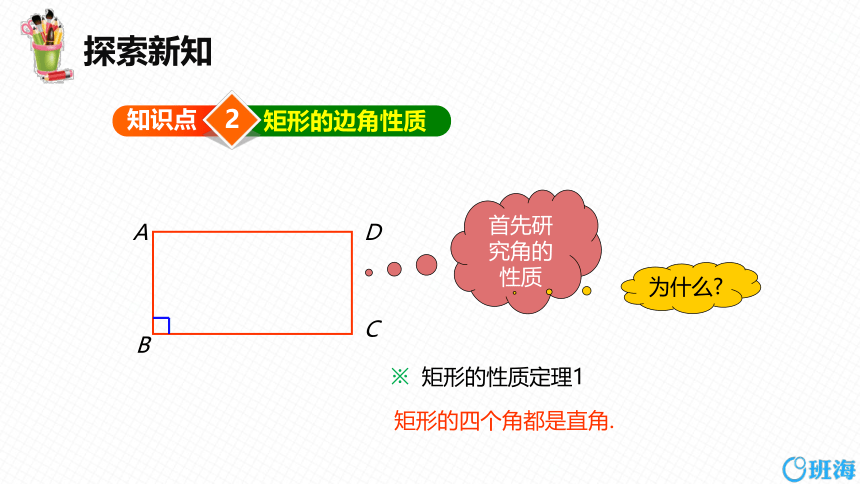
矩形的边角性质
首先研究角的性质
B
A
D
C
矩形的四个角都是直角.
为什么
※ 矩形的性质定理1
探索新知
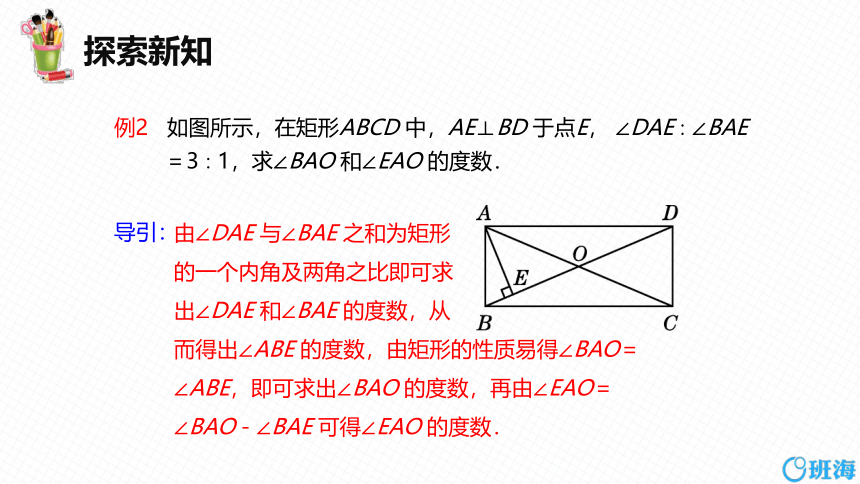
例2 如图所示,在矩形ABCD 中,AE⊥BD 于点E, ∠DAE∶∠BAE
=3∶1,求∠BAO 和∠EAO 的度数.
由∠DAE 与∠BAE 之和为矩形
的一个内角及两角之比即可求
出∠DAE 和∠BAE 的度数,从
而得出∠ABE 的度数,由矩形的性质易得∠BAO=
∠ABE,即可求出∠BAO 的度数,再由∠EAO=
∠BAO-∠BAE 可得∠EAO 的度数.
导引:
探索新知
∵四边形ABCD 是矩形,
∴∠DAB=90°,AO= AC,BO= BD,AC=BD.
∴∠BAE+∠DAE=90°,AO=BO.
又∵∠DAE∶∠BAE=3∶1,
∴∠BAE=22.5°,∠DAE=67.5°.
∵AE⊥BD,
∴∠ABE=90°-∠BAE=90°-22.5°=67.5°.
∵AO=BO,∴∠BAO=∠ABE=67.5°.
∴∠EAO=∠BAO-∠BAE=67.5°-22.5°=45°.
解:
探索新知
总 结
矩形的每条对角线把矩形分成两个直角三角形,矩形的两条对角线将矩形分成四个等腰三角形,因此有关矩形的计算问题经常通过转化到直角三角形和等腰三角形中来解决.
典题精讲
1
如图,点E 是矩形ABCD 的边AD 延长线上的一点,且AD=DE,连接BE 交CD 于点O,连接AO,下列结论中不正确的是( )
A.△AOB ≌ △BOC
B.△BOC ≌ △EOD
C.△AOD ≌ △EOD
D.△AOD ≌ △BOC
A
典题精讲
2
如图,点O 是矩形ABCD 的对角线AC 的中点,OM∥AB交AD 于点M,若OM=3,BC=10,则OB 的长为( )
A.5
B.4
C.
D.
D
探索新知
3
知识点
矩形的对角线性质
B
A
D
C
两条对角线有何关系
矩形的对角线相等.
※ 矩形的性质定理2
探索新知
任意画一个矩形,作出它的两条对角线,并比较它们的长.你有什么发现
已知:如图所示,四边形ABCD 是矩形.
求证:AC=DB.
∵四边形ABCD 是矩形,
∴∠ABC=∠DCB=90°(矩形的性质定理1).
∵AB=CD (平行四边形的对边相等),BC =CB.
∴△ABC ≌ △DCB (SAS). ∴AC=DB.
于是,就得到矩形的性质:矩形的对角线相等.
证明:
探索新知
例3 如图,矩形ABCD 的对角线 AC,BD 相交于点 O,
∠AOB=60°,AB=4.求矩形对角线的长.
∵四边形ABCD 是矩形,
∴AC 与BD 相等且互相平分.
∴OA=OB.
又 ∠AOB=60°,
∴△OAB 是等边三角形.
∴OA=AB=4.
∴ AC=BD=2OA=8.
解:
典题精讲
1
求证:矩形的对角线相等.
已知:如图,四边形ABCD 是
矩形,AC 与BD 相交于点O.
求证:AC=BD.
因为四边形ABCD 是矩形,
所以∠ABC=∠DCB=90°,AB=DC,
又BC=CB,
所以Rt△ABC ≌ Rt△DCB,
所以AC=DB,即AC=BD.
解:
证明:
典题精讲
2 一个矩形的一条对角线长为8,两条对角线的一
个交角为120°.求这个矩形的边长
(结果保留小数点后两位).
如图所示,在矩形ABCD 中,∠AOD=∠BOC=120°,所以∠AOB=∠COD=60°.因为AC=BD=8,所以OA=OB=OC=OD=4,
所以△AOB 为等边三角形,所以AB=OA=OB=4.
在Rt△ABD 中,AD= ≈6.93. 即这个矩形的边长分别为4,6.93,4,6.93.
解:
典题精讲
3
如图,在矩形ABCD 中,对角线AC,BD 相交于点O,∠AOB=60°,AC=6 cm,则AB 的长是( )
A.3 cm
B.6 cm
C.10 cm
D.12 cm
A
探索新知
4
知识点
直角三角形斜边上中线的性质
A
B
C
O
D
在左图的Rt△ABC中,OB与AC有
何关系?
D
直角三角形斜边上的中线等于斜边的一半.
※ 推 论
OB= AC
探索新知
例4 如图(1),BD,CE 是△ABC 的两条高,M,N 分别
是BC,DE 的中点.求证:MN⊥DE.
如图(2),连接EM,DM,由CE 与BD
为△ABC 的两条高,可得△BEC 与
△CDB 均为直角三角形,根据M 为BC
的中点,利用直角三角形斜边上的中线
等于斜边的一半,可得EM 为BC 的一半,
DM 也为BC 的一半,通过等量代换可得
EM=DM,又N 为DE 的中点,所以MN⊥DE.
(1)
(2)
导引:
探索新知
连接EM,DM,如图(2).
∵BD,CE 为△ABC 的两条高,
∴BD⊥AC,CE⊥AB,∴∠BEC=∠CDB=90°.
在Rt△BEC 中,∵M 为斜边BC 的中点,
∴EM= BC.
在Rt△CDB 中,∵M 为斜边BC 的中点,
∴DM= BC.
∴EM=DM.
又∵N 为DE 的中点,∴MN⊥DE.
证明:
(2)
探索新知
总 结
若题目中出现了一边的中点,往往需要用到中线,若又有直角,往往需要用到直角三角形斜边上的中线等于斜边的一半.
典题精讲
如图,P 是矩形ABCD 的对角线AC 的中点,E 是
AD 的中点.若AB=6,AD=8,则四边形ABPE
的周长为( )
A.14 B.16 C.17 D.18
D
典题精讲
2
如图,在△ABC 中,点D,E 分别是边AB,AC 的中点,AF⊥BC,垂足为点F,∠ADE=30°,DF=4,则BF 的长为( )
A.4
B.8
C.2
D.4
D
易错提醒
如图,AB=6,O 是AB 的中点,直线l 经过点O,∠1=120°,P 是直线l上一点,当△APB 为直角三角形时,AP=_______________.
易错点:对题意理解不透彻导致漏解.
3或3 或3
易错提醒
此题易因考虑不全而出错.当∠APB=90°时,分两种情况讨论.
情况一:如图①,∵O 为AB 的中点,
∴PO= AB,BO= AB.
∴PO=BO. ∴∠PBA=∠OPB.
∵∠1=120°,∴∠PBA=30°.
∴AP= AB=3;
易错提醒
情况二:如图②,∵AO=BO,∠APB=90°,
∴PO=BO. ∵∠1=120°,∴∠BOP=60°.
∴△BOP 为等边三角形.∴BP=OB= AB=3.
∴AP= ;
当∠BAP=90°时,如图③,
∵∠1=120°, ∴∠AOP=60°.
∴∠APO=30°. ∴PO=2AO=6.
∴AP= ;
易错提醒
当∠ABP=90°时,如图④,
∵∠1=120°,∴∠BOP=60°.
∴∠BPO=30°.∴PO=2BO=6.
∴BP= .
∴AP= .
学以致用
小试牛刀
1
如图,矩形ABCD 的对角线AC 与BD 相交于点O,CE∥BD,DE∥AC,AD=
DE=2,则四边形OCED 的面积为( )
A.2
B.4
C.4
D.8
A
小试牛刀
2
如图,点P 是矩形ABCD 的边AD上的一动点,矩形的两条边AB,BC 的长分别是6和8,则点P 到矩形的两条对角线AC 和BD 的距离之和是( )
A.4.8
B.5
C.6
D.7.2
A
小试牛刀
3
在 ABCD 中,AB=3,BC=4,连接AC,BD,当 ABCD 的面积最大时,下列结论正确的有( )
①AC=5 ; ②∠BAD+∠BCD=180°;
③AC⊥BD ; ④AC=BD.
A.①②③ B.①②④
C.②③④ D.①③④
B
小试牛刀
4
如图,在矩形纸片ABCD 中,AD=4 cm,把纸片沿直线AC折叠,点B 落在E 处,AE 交DC 于点O. 若AO=5 cm,则AB 的长为( )
A.6 cm
B.7 cm
C.8 cm
D.9 cm
C
小试牛刀
5
在探索“尺规三等分角”这个数学名题的过程中,曾利用了如图.该图中,四边形ABCD 是矩形,E 是BA 延长线上一点,F 是CE上一点,∠ACF=∠AFC,∠FAE=∠FEA. 若∠ACB=21°,则∠ECD 的度数是( )
A.7°
B.21°
C.23°
D.24°
C
小试牛刀
在矩形ABCD 中,E、F 分别是AD、BC 的中点,
CE、AF 分别交BD 于G、H 两点.
求证:(1)四边形AFCE 是平行四边形;
(2)EG=FH.
小试牛刀
(1)∵四边形ABCD 是矩形,
∴AD∥BC,AD=BC.
∵E、F 分别是AD、BC 的中点,
∴AE= AD,CF= BC.
∴AE=CF.
∴四边形AFCE 是平行四边形.
证明:
小试牛刀
(2)∵四边形AFCE 是平行四边形,
∴CE∥AF.
∴∠DGE=∠AHD=∠BHF.
∵AD∥BC,∴∠EDG=∠FBH.
∵DE= AD,BF= BC,AD=BC,
∴DE=BF.
在△DEG 和△BFH 中,
∴△DEG ≌ △BFH (AAS).
∴EG=FH.
小试牛刀
数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形
对角线上任一点作两条分别平行于两邻边的直线,则所容两长
方形面积相等(如图所示)”这一推论,他从这一推论出发,利用
“出入相补”原理复原了《海岛算经》九题古证.(以上材料来源
于《古证复原的原理》、《吴文俊与中国数学》和《古代世界数
学泰斗刘徵》)
小试牛刀
请根据该图完成这个推论的证明过程.
证明:S矩形NFGD=S△ADC-(S△ANF+S△FGC),S矩形EBMF=S△ABC-(________+________).
易知,S△ADC=S△ABC,________=________,________=________.
可得S矩形NFGD=S矩形EBMF
S△AEF
S△FMC
S△ANF
S△AEF
S△FGC
S△FMC
小试牛刀
如图,以△ABC 的三边为边在BC 的同侧分别作三个等边
三角形,即△ABD,△BCE,△ACF,连接DE,EF. 请回答
下列问题:
(1)四边形ADEF 是什么四边形?并说明理由.
(2)当△ABC 满足什么条件时,四边形ADEF 是矩形?
小试牛刀
(1)四边形ADEF 是平行四边形.
理由:∵△ABD,△BEC 都是等边三角形,
∴BD=AB=AD,BE=BC,
∠DBA=∠EBC=60°.
∴∠DBE=60°-∠EBA,∠ABC=60°-∠EBA.
∴∠DBE=∠ABC.
∴△DBE ≌ △ABC. ∴DE=AC.
又∵△ACF 是等边三角形,∴AC=AF. ∴DE=AF.
同理可得△ABC ≌ △FEC,∴EF=BA=DA.
∵DE=AF,DA=EF,
∴四边形ADEF 为平行四边形.
解:
小试牛刀
(2)若四边形ADEF 为矩形,则∠DAF=90°.
∵∠DAB=∠FAC=60°,
∴∠BAC=360°-∠DAB-∠FAC-∠DAF=360°
-60°-60°-90°=150°.
∴当△ABC 满足∠BAC=150°时,四边形ADEF 是矩形.
课堂小结
课堂小结
1.矩形定义:有一个角是直角的平行四边形叫做矩形,
具有平行四边形所有性质.
2.性质归纳:
矩形的四个角都是直角.
※ 矩形的性质定理1
矩形的对角线相等.
※ 矩形的性质定理2
※ 推 论
直角三角形斜边上的中线等于斜边的一半.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
18.2 特殊的平行四边形
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
1.什么叫平行四边形?
3.平行四边形有哪些性质?
①平行四边形的对角相等.
②平行四边形的对边相等.
③平行四边形的对角线互相平分.
2.平行四边形与四边形
有什么关系?
A
B
C
D
两组对边分别平行的四边形叫做平行四边形 .
特殊
一般
平行四边形
具有四边形的
一切性质
新课精讲
探索新知
1
知识点
矩形的定义
平行四边形
长方形
有一个角是直角
矩 形
有一个角是直角的平行四边形叫做矩形.
★矩形具有平行四边形的一切性质!
探索新知
有一个内角是直角的平行四边形叫矩形.
矩形定义:
A
B
C
D
∵在 ABCD 中,
∠A=90°
∴ ABCD 是矩形.
探索新知
例1 如图所示,l1∥l2,A、B 是l1上的两点,过A、B 分
别作l2的垂线,垂足分别为D、C.四
边形ABCD 是矩形吗 简述你的理由.
很容易发现ABCD 为平行四边形只需有一个角为
直角即可,因为AD⊥l2有直角,问题得证.
四边形ABCD 是矩形,理由:∵AD⊥l2,BC⊥l2,
∴AD∥BC.∵l1∥l2,
∴四边形ABCD 是平行四边形.
又∵∠ADC=90°,∴平行四边形ABCD 为矩形.
分析:
解:
探索新知
总 结
利用定义识别一个四边形是矩形,首先要证明四边形是平行四边形,然后证明平行四边形有一个角是直角.
典题精讲
1
矩形是轴对称图形吗?如果是,它有几条对称轴?
是,它有2条对称轴.
解:
2
下列说法不正确的是( )
A.矩形是平行四边形
B.矩形不一定是平行四边形
C.有一个角是直角的平行四边形是矩形
D.平行四边形具有的性质矩形都具有
B
探索新知
2
知识点
矩形的边角性质
首先研究角的性质
B
A
D
C
矩形的四个角都是直角.
为什么
※ 矩形的性质定理1
探索新知
例2 如图所示,在矩形ABCD 中,AE⊥BD 于点E, ∠DAE∶∠BAE
=3∶1,求∠BAO 和∠EAO 的度数.
由∠DAE 与∠BAE 之和为矩形
的一个内角及两角之比即可求
出∠DAE 和∠BAE 的度数,从
而得出∠ABE 的度数,由矩形的性质易得∠BAO=
∠ABE,即可求出∠BAO 的度数,再由∠EAO=
∠BAO-∠BAE 可得∠EAO 的度数.
导引:
探索新知
∵四边形ABCD 是矩形,
∴∠DAB=90°,AO= AC,BO= BD,AC=BD.
∴∠BAE+∠DAE=90°,AO=BO.
又∵∠DAE∶∠BAE=3∶1,
∴∠BAE=22.5°,∠DAE=67.5°.
∵AE⊥BD,
∴∠ABE=90°-∠BAE=90°-22.5°=67.5°.
∵AO=BO,∴∠BAO=∠ABE=67.5°.
∴∠EAO=∠BAO-∠BAE=67.5°-22.5°=45°.
解:
探索新知
总 结
矩形的每条对角线把矩形分成两个直角三角形,矩形的两条对角线将矩形分成四个等腰三角形,因此有关矩形的计算问题经常通过转化到直角三角形和等腰三角形中来解决.
典题精讲
1
如图,点E 是矩形ABCD 的边AD 延长线上的一点,且AD=DE,连接BE 交CD 于点O,连接AO,下列结论中不正确的是( )
A.△AOB ≌ △BOC
B.△BOC ≌ △EOD
C.△AOD ≌ △EOD
D.△AOD ≌ △BOC
A
典题精讲
2
如图,点O 是矩形ABCD 的对角线AC 的中点,OM∥AB交AD 于点M,若OM=3,BC=10,则OB 的长为( )
A.5
B.4
C.
D.
D
探索新知
3
知识点
矩形的对角线性质
B
A
D
C
两条对角线有何关系
矩形的对角线相等.
※ 矩形的性质定理2
探索新知
任意画一个矩形,作出它的两条对角线,并比较它们的长.你有什么发现
已知:如图所示,四边形ABCD 是矩形.
求证:AC=DB.
∵四边形ABCD 是矩形,
∴∠ABC=∠DCB=90°(矩形的性质定理1).
∵AB=CD (平行四边形的对边相等),BC =CB.
∴△ABC ≌ △DCB (SAS). ∴AC=DB.
于是,就得到矩形的性质:矩形的对角线相等.
证明:
探索新知
例3 如图,矩形ABCD 的对角线 AC,BD 相交于点 O,
∠AOB=60°,AB=4.求矩形对角线的长.
∵四边形ABCD 是矩形,
∴AC 与BD 相等且互相平分.
∴OA=OB.
又 ∠AOB=60°,
∴△OAB 是等边三角形.
∴OA=AB=4.
∴ AC=BD=2OA=8.
解:
典题精讲
1
求证:矩形的对角线相等.
已知:如图,四边形ABCD 是
矩形,AC 与BD 相交于点O.
求证:AC=BD.
因为四边形ABCD 是矩形,
所以∠ABC=∠DCB=90°,AB=DC,
又BC=CB,
所以Rt△ABC ≌ Rt△DCB,
所以AC=DB,即AC=BD.
解:
证明:
典题精讲
2 一个矩形的一条对角线长为8,两条对角线的一
个交角为120°.求这个矩形的边长
(结果保留小数点后两位).
如图所示,在矩形ABCD 中,∠AOD=∠BOC=120°,所以∠AOB=∠COD=60°.因为AC=BD=8,所以OA=OB=OC=OD=4,
所以△AOB 为等边三角形,所以AB=OA=OB=4.
在Rt△ABD 中,AD= ≈6.93. 即这个矩形的边长分别为4,6.93,4,6.93.
解:
典题精讲
3
如图,在矩形ABCD 中,对角线AC,BD 相交于点O,∠AOB=60°,AC=6 cm,则AB 的长是( )
A.3 cm
B.6 cm
C.10 cm
D.12 cm
A
探索新知
4
知识点
直角三角形斜边上中线的性质
A
B
C
O
D
在左图的Rt△ABC中,OB与AC有
何关系?
D
直角三角形斜边上的中线等于斜边的一半.
※ 推 论
OB= AC
探索新知
例4 如图(1),BD,CE 是△ABC 的两条高,M,N 分别
是BC,DE 的中点.求证:MN⊥DE.
如图(2),连接EM,DM,由CE 与BD
为△ABC 的两条高,可得△BEC 与
△CDB 均为直角三角形,根据M 为BC
的中点,利用直角三角形斜边上的中线
等于斜边的一半,可得EM 为BC 的一半,
DM 也为BC 的一半,通过等量代换可得
EM=DM,又N 为DE 的中点,所以MN⊥DE.
(1)
(2)
导引:
探索新知
连接EM,DM,如图(2).
∵BD,CE 为△ABC 的两条高,
∴BD⊥AC,CE⊥AB,∴∠BEC=∠CDB=90°.
在Rt△BEC 中,∵M 为斜边BC 的中点,
∴EM= BC.
在Rt△CDB 中,∵M 为斜边BC 的中点,
∴DM= BC.
∴EM=DM.
又∵N 为DE 的中点,∴MN⊥DE.
证明:
(2)
探索新知
总 结
若题目中出现了一边的中点,往往需要用到中线,若又有直角,往往需要用到直角三角形斜边上的中线等于斜边的一半.
典题精讲
如图,P 是矩形ABCD 的对角线AC 的中点,E 是
AD 的中点.若AB=6,AD=8,则四边形ABPE
的周长为( )
A.14 B.16 C.17 D.18
D
典题精讲
2
如图,在△ABC 中,点D,E 分别是边AB,AC 的中点,AF⊥BC,垂足为点F,∠ADE=30°,DF=4,则BF 的长为( )
A.4
B.8
C.2
D.4
D
易错提醒
如图,AB=6,O 是AB 的中点,直线l 经过点O,∠1=120°,P 是直线l上一点,当△APB 为直角三角形时,AP=_______________.
易错点:对题意理解不透彻导致漏解.
3或3 或3
易错提醒
此题易因考虑不全而出错.当∠APB=90°时,分两种情况讨论.
情况一:如图①,∵O 为AB 的中点,
∴PO= AB,BO= AB.
∴PO=BO. ∴∠PBA=∠OPB.
∵∠1=120°,∴∠PBA=30°.
∴AP= AB=3;
易错提醒
情况二:如图②,∵AO=BO,∠APB=90°,
∴PO=BO. ∵∠1=120°,∴∠BOP=60°.
∴△BOP 为等边三角形.∴BP=OB= AB=3.
∴AP= ;
当∠BAP=90°时,如图③,
∵∠1=120°, ∴∠AOP=60°.
∴∠APO=30°. ∴PO=2AO=6.
∴AP= ;
易错提醒
当∠ABP=90°时,如图④,
∵∠1=120°,∴∠BOP=60°.
∴∠BPO=30°.∴PO=2BO=6.
∴BP= .
∴AP= .
学以致用
小试牛刀
1
如图,矩形ABCD 的对角线AC 与BD 相交于点O,CE∥BD,DE∥AC,AD=
DE=2,则四边形OCED 的面积为( )
A.2
B.4
C.4
D.8
A
小试牛刀
2
如图,点P 是矩形ABCD 的边AD上的一动点,矩形的两条边AB,BC 的长分别是6和8,则点P 到矩形的两条对角线AC 和BD 的距离之和是( )
A.4.8
B.5
C.6
D.7.2
A
小试牛刀
3
在 ABCD 中,AB=3,BC=4,连接AC,BD,当 ABCD 的面积最大时,下列结论正确的有( )
①AC=5 ; ②∠BAD+∠BCD=180°;
③AC⊥BD ; ④AC=BD.
A.①②③ B.①②④
C.②③④ D.①③④
B
小试牛刀
4
如图,在矩形纸片ABCD 中,AD=4 cm,把纸片沿直线AC折叠,点B 落在E 处,AE 交DC 于点O. 若AO=5 cm,则AB 的长为( )
A.6 cm
B.7 cm
C.8 cm
D.9 cm
C
小试牛刀
5
在探索“尺规三等分角”这个数学名题的过程中,曾利用了如图.该图中,四边形ABCD 是矩形,E 是BA 延长线上一点,F 是CE上一点,∠ACF=∠AFC,∠FAE=∠FEA. 若∠ACB=21°,则∠ECD 的度数是( )
A.7°
B.21°
C.23°
D.24°
C
小试牛刀
在矩形ABCD 中,E、F 分别是AD、BC 的中点,
CE、AF 分别交BD 于G、H 两点.
求证:(1)四边形AFCE 是平行四边形;
(2)EG=FH.
小试牛刀
(1)∵四边形ABCD 是矩形,
∴AD∥BC,AD=BC.
∵E、F 分别是AD、BC 的中点,
∴AE= AD,CF= BC.
∴AE=CF.
∴四边形AFCE 是平行四边形.
证明:
小试牛刀
(2)∵四边形AFCE 是平行四边形,
∴CE∥AF.
∴∠DGE=∠AHD=∠BHF.
∵AD∥BC,∴∠EDG=∠FBH.
∵DE= AD,BF= BC,AD=BC,
∴DE=BF.
在△DEG 和△BFH 中,
∴△DEG ≌ △BFH (AAS).
∴EG=FH.
小试牛刀
数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形
对角线上任一点作两条分别平行于两邻边的直线,则所容两长
方形面积相等(如图所示)”这一推论,他从这一推论出发,利用
“出入相补”原理复原了《海岛算经》九题古证.(以上材料来源
于《古证复原的原理》、《吴文俊与中国数学》和《古代世界数
学泰斗刘徵》)
小试牛刀
请根据该图完成这个推论的证明过程.
证明:S矩形NFGD=S△ADC-(S△ANF+S△FGC),S矩形EBMF=S△ABC-(________+________).
易知,S△ADC=S△ABC,________=________,________=________.
可得S矩形NFGD=S矩形EBMF
S△AEF
S△FMC
S△ANF
S△AEF
S△FGC
S△FMC
小试牛刀
如图,以△ABC 的三边为边在BC 的同侧分别作三个等边
三角形,即△ABD,△BCE,△ACF,连接DE,EF. 请回答
下列问题:
(1)四边形ADEF 是什么四边形?并说明理由.
(2)当△ABC 满足什么条件时,四边形ADEF 是矩形?
小试牛刀
(1)四边形ADEF 是平行四边形.
理由:∵△ABD,△BEC 都是等边三角形,
∴BD=AB=AD,BE=BC,
∠DBA=∠EBC=60°.
∴∠DBE=60°-∠EBA,∠ABC=60°-∠EBA.
∴∠DBE=∠ABC.
∴△DBE ≌ △ABC. ∴DE=AC.
又∵△ACF 是等边三角形,∴AC=AF. ∴DE=AF.
同理可得△ABC ≌ △FEC,∴EF=BA=DA.
∵DE=AF,DA=EF,
∴四边形ADEF 为平行四边形.
解:
小试牛刀
(2)若四边形ADEF 为矩形,则∠DAF=90°.
∵∠DAB=∠FAC=60°,
∴∠BAC=360°-∠DAB-∠FAC-∠DAF=360°
-60°-60°-90°=150°.
∴当△ABC 满足∠BAC=150°时,四边形ADEF 是矩形.
课堂小结
课堂小结
1.矩形定义:有一个角是直角的平行四边形叫做矩形,
具有平行四边形所有性质.
2.性质归纳:
矩形的四个角都是直角.
※ 矩形的性质定理1
矩形的对角线相等.
※ 矩形的性质定理2
※ 推 论
直角三角形斜边上的中线等于斜边的一半.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
