【班海精品】人教版(新)八下-19.1 函数 第四课时【优质课件】
文档属性
| 名称 | 【班海精品】人教版(新)八下-19.1 函数 第四课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 6.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 10:20:43 | ||
图片预览











文档简介
(共43张PPT)
19.1 函数
第4课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
某公司招聘
条件:初中学历以上,团员优先,能吃苦耐劳
年舲:16-25岁
待遇:按钟点计酬(工资标准为每小时8元)
假如你是初中毕业生被聘用,设工作时数为t (时),应得
工资额为m (元),则m=8t.
取一些不同的t 的值,求出相应的m 的值:
t= 2 时,m= 16 元;t= 3 时,m= 24 元;
…….
在根据不同的工作时数计算你应得工资额的过程中你用了函数的哪些表示方法呢?
新课精讲
探索新知
1
知识点
函数的表示法
函数的表示法:
可以用三种方法:
①图象法
②列表法
③关系式法
探索新知
用来表达函数关系的数学式子叫做函数解析式或函数关系式.
(1)用关于自变量的数学式子表示函数与自变量的方叫做解析式法.
(2)用表格表示函数关系的方法,叫做列表法.
(3)用图象表示函数关系的方法.叫做图象法.
探索新知
例1
一个水库的水位在最近5 h内持续上涨.下表记录了这5 h内6个时间点的水位高度,其中t 表示时间,y表示水位高度.
(1)在平面直角坐标系中描出表中数据对应的点,这些点是
否在一条直线上?由此你能发现水位变化有什么规律吗?
(2)水位高度y是否为时间t的函数?如果是,试写出一个符
合表中数据的函数解析式,并画出这个函数的图象.这个
函数能表示水位的变化规律吗?
(3)据估计这种上涨规律还会持续2 h,预测再过2 h水位高
度将为多少米.
t/h 0 1 2 3 4 5
y/m 3 3.3 3.6 3.9 4.2 4.5
探索新知
(1)如图,描出表中数据对应的点.可以看出,这6个点
在一条直线上.再结合表中数据,可以发现每小时水
位上升0.3m.由此猜想,如果画出这5 h内其他时刻
(如t=2. 5 h等)及其水位高度所对应的点,它们可能
也在这条直线上,即在这
个时间段中水位可能是始
终以同一速度均匀上升的.
解:
探索新知
(2) 由于水位在最近5 h内持续上涨,对于时间 t 的每一个确定的值,水位高度 y 都有唯一的值与其对应,所以y 是t 的函数.开始时水位高度为3 m,以后每小时水位上升0.3 m.函数y=0. 3t+3(0≤t≤5)是符合表中数据的一个函数,它表示经过t h水位上升0.3t m,即水位y 为(0. 3t+3)m.其图象是(1)图中点A (0, 3) 和点B (5, 4.5)之间的线段AB.
如果在这5 h内,水位一直匀速上升, 即升速为0.3m/h,那么函数 y=0.3t+3(0≤t≤5)就精确地表示了这种变化规律.即使在这5 h内,水位的升速有些变化,而由于每小时水位上升0.3 m是确定的,因此这个函数也可以近似地表示水位的变化规律.
探索新知
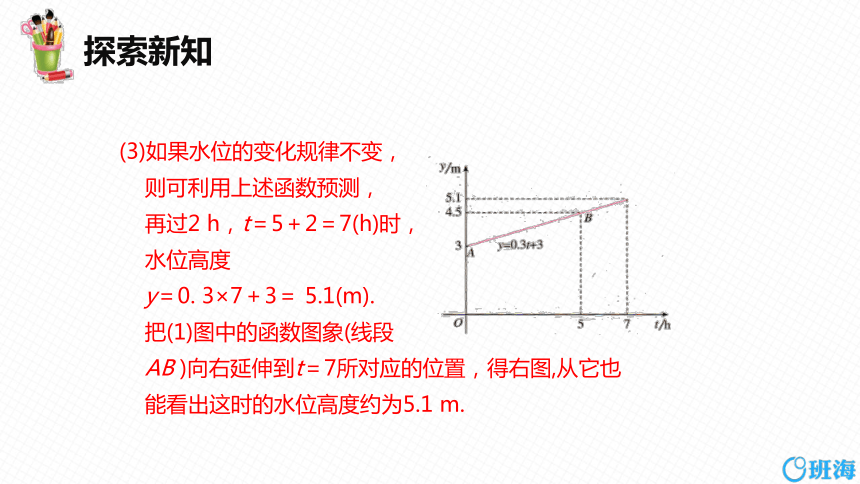
(3)如果水位的变化规律不变,
则可利用上述函数预测,
再过2 h,t=5+2=7(h)时,
水位高度
y=0. 3×7+3= 5.1(m).
把(1)图中的函数图象(线段
AB )向右延伸到t=7所对应的位置,得右图,从它也
能看出这时的水位高度约为5.1 m.
探索新知
(1)从图中获取信息首先要弄清楚横、纵轴分别表示什么意义,再对问题进行分析.
(2)在实际问题中,有的横轴和纵轴上的单位长度可以不一致,这对问题的结论没有影响,但每条坐标轴上的单位长度必须要一致.
总 结
典题精讲
1
用列表法与解析式法表示n 边形的内角和m (单位:度)
关于边数n 的函数.
列表法:
解:
多边形的边数n 3 4 5 6 …
内角和m 180° 360° 540° 720° …
解析式法:m=(n-2)·180°(n≥3,n 为正整数).
典题精讲
2
用解析式法与图象法表示等边三角形的周长l 关于
边长a 的函数.
解:
解析式法:l=3a (a>0).
图象法:函数图象如图.
典题精讲
3
若每上6个台阶就升高1米,则上升高度h (米)与上的台阶数m (个)之间的函数解析式是( )
A.h=6m B.h=6+m
C.h=m-6 D.h=
D
a. 解析式法
购买该品牌东北大米的质量x (kg) 1 2 3 4 5 6 …
付款金额y (元) …
典题精讲
b. 列表法
4
已知某品牌东北大米6元/kg,请你根据条件完成下表:
6 12 18 24 30 36
典题精讲
c. 图象法
5
小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,看成一个容器,然后,小明对准玻璃杯口匀速注水,如图所示,在注水过程中,杯底始终紧贴鱼缸底部,则下面可以近似地刻画
出容器最高水位h 与注水时间t 之间的
变化情况的是( )
D
探索新知
2
知识点
三种函数表示法间的关系
注意:
列表法、图象法、解析法虽然形式不同、但都反映了问题中的两个变量——x 自变量)、y (函数)的关系.我们在解决问题时,常常综合运用这三种表示法来深入地研究自变量与函数的关系式的性质.同一个函数关系可以用不同的方法表示.
探索新知
例2
某年初,我国西南部分省市遭
遇了严重干旱.某水库的蓄水
量随着时间的增加而减小,干
旱持续时间t (天)与蓄水量V (万
立方米)的变化情况如图所示,
根据图象回答问题:
(1)这个图象反映了哪两个变量之间的关系?
(2)根据图象填表:
(3)当t 取0至60天之间的任一值时,对应几个V 值?
(4)V 可以看作t 的函数吗?若可以,写出函数解析式.
干旱持续时间t/天 0 10 20 30 40 50 60
蓄水量V/万立方米
探索新知
(1)通过读图可知,横坐标表示干旱持续时间,纵坐标表
示水库蓄水量,因此它表示的是干旱持续时间与水库
蓄水量之间的关系;
(2)根据图象信息确定每个特殊点的坐标即可;
(3)观察图象可得;
(4)可根据函数的定义来判断.
(1)图象反映了干旱持续时间与水库蓄水量之间的关系.
(2)填表如下:
导引:
解:
干旱持续时间t/天 0 10 20 30 40 50 60
蓄水量V/万立方米 1 200 1 000 800 600 400 200 0
探索新知
(3)当t 取0至60天之间的任一值时,对应着一个V 值.
(4)V 可以看作t 的函数.
根据图象可知,该水库初始蓄水量为1 200万立方米,
干旱每持续10天,蓄水量相应减少200万立方米,由
此可得出函数解析式为
V=1 200- =-20t+1 200(0≤t≤60).
探索新知
本例通过“形”,即图象中的信息,用列表及解析式这些“数”来表示说明,三种函数表示方法之间有互补性,是可以相互转化的,体现了数形结合思想的应用.
总 结
典题精讲
1
一条小船沿直线向码头匀速前进. 在0min,2min,4min,6min时,测得小船与码头的距离分别为200 m,150 m,100 m,50 m. 小船与码头的距离s 是时间t 的函数吗?如果是,写出函数解析式,并画出函数图象. 如果船速不变, 多长时间后小船到达码头?
解:
s 是t 的函数,函数解析式为:s=200-25t (0≤t≤8),函数图象如图.如果船速不变,8 min后小船到达码头.
典题精讲
常用的三种函数的表示方法是:________、________、________,其中________可以由表中已有自变量的每一个值直接得出相应的函数值;__________能准确地反映整个变化过程中函数与自变量之间的关系;________能直观、形象地表示函数关系.
2
图象法
列表法
解析式法
列表法
解析式法
图象法
要形象、直观地表示某市某天的气温与时间的函数关系,适宜用( )
A.列表法 B.解析式法
C.图象法 D.以上都可以
3
C
典题精讲
下面说法中正确的是( )
A.两个变量间的关系只能用解析式表示
B.图象不能直观地表示两个变量间的数量关系
C.借助表格可以反映出因变量随自变量的变化情况
D.以上说法都不对
4
C
典题精讲
某下岗职工购进一批苹果,到集贸市场零售,已知卖出的苹果质量x (kg)与收入y (元)的关系如下表:则收入y (元)与卖出的苹果质量x (kg)之间的函数解析式为( )
A.y=2x+0.1 B.y=2x
C.y=2x+0.5 D.y=2.1x
5
质量x/kg 1 2 3 4 5 …
收入y/元 2+0.1 4+0.2 6+0.3 8+0.4 10+0.5 …
D
易错提醒
如图,A,B 是半径为1的⊙O上两点,且OA⊥OB,
点P 从点A出发,在⊙O上以每秒一个单位长度的速
度匀速运动,回到点A运动结束,设运动时间为x
(单位:s),弦BP 的长为y,那么下列图象中可能表
示y 与x 函数关系的是( )
A.① B.④ C.②或④ D.①或③
D
易错点:不注意分类导致漏解而致错.
学以致用
小试牛刀
1
如图,△ABC 的边BC 长是8,BC 边上的高AD ′是4,点D在BC 上运动(不与C 点重合),设BD 长为x,则△ACD 的面积y 与x 之间的函数关系式为_______________________.
y=16-2x (0≤x<8)
小试牛刀
某省遭受台风袭击,大部分地区发生强降雨,某河受暴雨袭击,某天的水位记录如表,观察表中数据,水位上升最快的时段是( )
A. 8~12时 B.12~16时
C.16~20时 D.20~24时
2
时间/时 0 4 8 12 16 20 24
水位/米 2 2.5 3 4 5 6 8
D
小试牛刀
八(1)班同学在探究弹簧长度与砝码质量的关系时,实验得到的相应数据如下表所示:则y 关于x 的函数图象是( )
3
砝码质量 x/ 克 0 50 100 150 200 250 300 400 500
弹簧长度 y/ 厘米 2 3 4 5 6 7 7.5 7.5 7.5
D
小试牛刀
4 如图,已知函数y=kx+n 的图象是一条直线,且图象
经过两点,两点坐标分别是A (-1,3)与B (3,-3).
(1)试确定k 和n 的值;
(2)判断函数图象是否经过点C (-5,9),D (-6,10),
并说明原因.
小试牛刀
(1)已知图象经过的点的坐标,表示坐标的有序实数对适合函数解析式,因此代入已知两点的坐标的有序实数对得出方程组,即可确定k 和n 的值.(2)将点C,D 的坐标分别代入求出的函数解析式y=kx+n 中即可,若等式成立,则图象经过该点,否则不经过.
思路导引:
(1)分别把点A,B 的坐标代入函数的解析式,得方程组
解得
所以k 和n 的值分别为 .
解:
小试牛刀
(2)由(1)知函数的解析式是y=- x+ .把x=-5代入函数
的解析式,得y=- x+ =- ×(-5)+ =9,因此
图象经过点C (-5,9).
同理当x=-6时,y=- x+ =- ×(-6)+
= ≠10,
因此图象不经过点D (-6,10).
小试牛刀
判断某点是否在函数的图象上的方法:将该点的横坐标代入函数解析式,看求出的函数值是否等于纵坐标.若相等,则该点在函数的图象上;反之,则该点不在函数的图象上.
方法总结:
小试牛刀
5 已知函数y 与自变量x 之间成反比例关系,下表给出了
x 与y 的一些值:
(1)写出这个函数的解析式;
(2)根据函数解析式计算当x 的取值分别是-6和5时的函数值,
计算函数值分别是-12和36时的自变量的值.
x … -3 -2 -1 1 2 3 …
y … 1 2 4 -4 -2 -1 …
小试牛刀
(1)由表中的数据可知xy=-2,
所以函数的解析式是y=- .
(2)当x=-6时,函数值y=- = .
当x=5时,函数值y=- .
因为y=- ,所以x=- .
因此当y=-12时,x=- = .
当y=36时,x=- =- .
解:
小试牛刀
6 一个小球由静止开始从一个斜坡上向下滚动,滚动的
距离s (m)与时间t (s)之间的函数解析式为s=2t 2(t ≥0).
(1)根据解析式完成下表,并画出图象;
(2)当小球滚动6.5 s时,其滚动的距离是多少?
(3)经过多少秒,小球滚动的距离是128 m
时间t/s 1 2 3 4
距离s/m
2
8
18
32
小试牛刀
(1)这个函数的图象如图.
(2)当t=6.5时,s=84.5,即当小球滚动6.5 s时,其
滚动的距离是84.5 m.
(3)当s=128时,t=8,即经过8 s,小球滚动的距离
是128 m.
解:
小试牛刀
如图,点P 是 ABCD 边上一动点,沿A→D→C→B 的路径移动,
设P 点经过的路径长为x,△BAP 的面积是y,则下列能大致反映
y 与x 的函数关系的图象是( )
A
课堂小结
课堂小结
函数的表示方法共有三种:
列表法、解析式法、图象法,它们分别从数、
式和形的角度反映了函数的本质.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
19.1 函数
第4课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
某公司招聘
条件:初中学历以上,团员优先,能吃苦耐劳
年舲:16-25岁
待遇:按钟点计酬(工资标准为每小时8元)
假如你是初中毕业生被聘用,设工作时数为t (时),应得
工资额为m (元),则m=8t.
取一些不同的t 的值,求出相应的m 的值:
t= 2 时,m= 16 元;t= 3 时,m= 24 元;
…….
在根据不同的工作时数计算你应得工资额的过程中你用了函数的哪些表示方法呢?
新课精讲
探索新知
1
知识点
函数的表示法
函数的表示法:
可以用三种方法:
①图象法
②列表法
③关系式法
探索新知
用来表达函数关系的数学式子叫做函数解析式或函数关系式.
(1)用关于自变量的数学式子表示函数与自变量的方叫做解析式法.
(2)用表格表示函数关系的方法,叫做列表法.
(3)用图象表示函数关系的方法.叫做图象法.
探索新知
例1
一个水库的水位在最近5 h内持续上涨.下表记录了这5 h内6个时间点的水位高度,其中t 表示时间,y表示水位高度.
(1)在平面直角坐标系中描出表中数据对应的点,这些点是
否在一条直线上?由此你能发现水位变化有什么规律吗?
(2)水位高度y是否为时间t的函数?如果是,试写出一个符
合表中数据的函数解析式,并画出这个函数的图象.这个
函数能表示水位的变化规律吗?
(3)据估计这种上涨规律还会持续2 h,预测再过2 h水位高
度将为多少米.
t/h 0 1 2 3 4 5
y/m 3 3.3 3.6 3.9 4.2 4.5
探索新知
(1)如图,描出表中数据对应的点.可以看出,这6个点
在一条直线上.再结合表中数据,可以发现每小时水
位上升0.3m.由此猜想,如果画出这5 h内其他时刻
(如t=2. 5 h等)及其水位高度所对应的点,它们可能
也在这条直线上,即在这
个时间段中水位可能是始
终以同一速度均匀上升的.
解:
探索新知
(2) 由于水位在最近5 h内持续上涨,对于时间 t 的每一个确定的值,水位高度 y 都有唯一的值与其对应,所以y 是t 的函数.开始时水位高度为3 m,以后每小时水位上升0.3 m.函数y=0. 3t+3(0≤t≤5)是符合表中数据的一个函数,它表示经过t h水位上升0.3t m,即水位y 为(0. 3t+3)m.其图象是(1)图中点A (0, 3) 和点B (5, 4.5)之间的线段AB.
如果在这5 h内,水位一直匀速上升, 即升速为0.3m/h,那么函数 y=0.3t+3(0≤t≤5)就精确地表示了这种变化规律.即使在这5 h内,水位的升速有些变化,而由于每小时水位上升0.3 m是确定的,因此这个函数也可以近似地表示水位的变化规律.
探索新知
(3)如果水位的变化规律不变,
则可利用上述函数预测,
再过2 h,t=5+2=7(h)时,
水位高度
y=0. 3×7+3= 5.1(m).
把(1)图中的函数图象(线段
AB )向右延伸到t=7所对应的位置,得右图,从它也
能看出这时的水位高度约为5.1 m.
探索新知
(1)从图中获取信息首先要弄清楚横、纵轴分别表示什么意义,再对问题进行分析.
(2)在实际问题中,有的横轴和纵轴上的单位长度可以不一致,这对问题的结论没有影响,但每条坐标轴上的单位长度必须要一致.
总 结
典题精讲
1
用列表法与解析式法表示n 边形的内角和m (单位:度)
关于边数n 的函数.
列表法:
解:
多边形的边数n 3 4 5 6 …
内角和m 180° 360° 540° 720° …
解析式法:m=(n-2)·180°(n≥3,n 为正整数).
典题精讲
2
用解析式法与图象法表示等边三角形的周长l 关于
边长a 的函数.
解:
解析式法:l=3a (a>0).
图象法:函数图象如图.
典题精讲
3
若每上6个台阶就升高1米,则上升高度h (米)与上的台阶数m (个)之间的函数解析式是( )
A.h=6m B.h=6+m
C.h=m-6 D.h=
D
a. 解析式法
购买该品牌东北大米的质量x (kg) 1 2 3 4 5 6 …
付款金额y (元) …
典题精讲
b. 列表法
4
已知某品牌东北大米6元/kg,请你根据条件完成下表:
6 12 18 24 30 36
典题精讲
c. 图象法
5
小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,看成一个容器,然后,小明对准玻璃杯口匀速注水,如图所示,在注水过程中,杯底始终紧贴鱼缸底部,则下面可以近似地刻画
出容器最高水位h 与注水时间t 之间的
变化情况的是( )
D
探索新知
2
知识点
三种函数表示法间的关系
注意:
列表法、图象法、解析法虽然形式不同、但都反映了问题中的两个变量——x 自变量)、y (函数)的关系.我们在解决问题时,常常综合运用这三种表示法来深入地研究自变量与函数的关系式的性质.同一个函数关系可以用不同的方法表示.
探索新知
例2
某年初,我国西南部分省市遭
遇了严重干旱.某水库的蓄水
量随着时间的增加而减小,干
旱持续时间t (天)与蓄水量V (万
立方米)的变化情况如图所示,
根据图象回答问题:
(1)这个图象反映了哪两个变量之间的关系?
(2)根据图象填表:
(3)当t 取0至60天之间的任一值时,对应几个V 值?
(4)V 可以看作t 的函数吗?若可以,写出函数解析式.
干旱持续时间t/天 0 10 20 30 40 50 60
蓄水量V/万立方米
探索新知
(1)通过读图可知,横坐标表示干旱持续时间,纵坐标表
示水库蓄水量,因此它表示的是干旱持续时间与水库
蓄水量之间的关系;
(2)根据图象信息确定每个特殊点的坐标即可;
(3)观察图象可得;
(4)可根据函数的定义来判断.
(1)图象反映了干旱持续时间与水库蓄水量之间的关系.
(2)填表如下:
导引:
解:
干旱持续时间t/天 0 10 20 30 40 50 60
蓄水量V/万立方米 1 200 1 000 800 600 400 200 0
探索新知
(3)当t 取0至60天之间的任一值时,对应着一个V 值.
(4)V 可以看作t 的函数.
根据图象可知,该水库初始蓄水量为1 200万立方米,
干旱每持续10天,蓄水量相应减少200万立方米,由
此可得出函数解析式为
V=1 200- =-20t+1 200(0≤t≤60).
探索新知
本例通过“形”,即图象中的信息,用列表及解析式这些“数”来表示说明,三种函数表示方法之间有互补性,是可以相互转化的,体现了数形结合思想的应用.
总 结
典题精讲
1
一条小船沿直线向码头匀速前进. 在0min,2min,4min,6min时,测得小船与码头的距离分别为200 m,150 m,100 m,50 m. 小船与码头的距离s 是时间t 的函数吗?如果是,写出函数解析式,并画出函数图象. 如果船速不变, 多长时间后小船到达码头?
解:
s 是t 的函数,函数解析式为:s=200-25t (0≤t≤8),函数图象如图.如果船速不变,8 min后小船到达码头.
典题精讲
常用的三种函数的表示方法是:________、________、________,其中________可以由表中已有自变量的每一个值直接得出相应的函数值;__________能准确地反映整个变化过程中函数与自变量之间的关系;________能直观、形象地表示函数关系.
2
图象法
列表法
解析式法
列表法
解析式法
图象法
要形象、直观地表示某市某天的气温与时间的函数关系,适宜用( )
A.列表法 B.解析式法
C.图象法 D.以上都可以
3
C
典题精讲
下面说法中正确的是( )
A.两个变量间的关系只能用解析式表示
B.图象不能直观地表示两个变量间的数量关系
C.借助表格可以反映出因变量随自变量的变化情况
D.以上说法都不对
4
C
典题精讲
某下岗职工购进一批苹果,到集贸市场零售,已知卖出的苹果质量x (kg)与收入y (元)的关系如下表:则收入y (元)与卖出的苹果质量x (kg)之间的函数解析式为( )
A.y=2x+0.1 B.y=2x
C.y=2x+0.5 D.y=2.1x
5
质量x/kg 1 2 3 4 5 …
收入y/元 2+0.1 4+0.2 6+0.3 8+0.4 10+0.5 …
D
易错提醒
如图,A,B 是半径为1的⊙O上两点,且OA⊥OB,
点P 从点A出发,在⊙O上以每秒一个单位长度的速
度匀速运动,回到点A运动结束,设运动时间为x
(单位:s),弦BP 的长为y,那么下列图象中可能表
示y 与x 函数关系的是( )
A.① B.④ C.②或④ D.①或③
D
易错点:不注意分类导致漏解而致错.
学以致用
小试牛刀
1
如图,△ABC 的边BC 长是8,BC 边上的高AD ′是4,点D在BC 上运动(不与C 点重合),设BD 长为x,则△ACD 的面积y 与x 之间的函数关系式为_______________________.
y=16-2x (0≤x<8)
小试牛刀
某省遭受台风袭击,大部分地区发生强降雨,某河受暴雨袭击,某天的水位记录如表,观察表中数据,水位上升最快的时段是( )
A. 8~12时 B.12~16时
C.16~20时 D.20~24时
2
时间/时 0 4 8 12 16 20 24
水位/米 2 2.5 3 4 5 6 8
D
小试牛刀
八(1)班同学在探究弹簧长度与砝码质量的关系时,实验得到的相应数据如下表所示:则y 关于x 的函数图象是( )
3
砝码质量 x/ 克 0 50 100 150 200 250 300 400 500
弹簧长度 y/ 厘米 2 3 4 5 6 7 7.5 7.5 7.5
D
小试牛刀
4 如图,已知函数y=kx+n 的图象是一条直线,且图象
经过两点,两点坐标分别是A (-1,3)与B (3,-3).
(1)试确定k 和n 的值;
(2)判断函数图象是否经过点C (-5,9),D (-6,10),
并说明原因.
小试牛刀
(1)已知图象经过的点的坐标,表示坐标的有序实数对适合函数解析式,因此代入已知两点的坐标的有序实数对得出方程组,即可确定k 和n 的值.(2)将点C,D 的坐标分别代入求出的函数解析式y=kx+n 中即可,若等式成立,则图象经过该点,否则不经过.
思路导引:
(1)分别把点A,B 的坐标代入函数的解析式,得方程组
解得
所以k 和n 的值分别为 .
解:
小试牛刀
(2)由(1)知函数的解析式是y=- x+ .把x=-5代入函数
的解析式,得y=- x+ =- ×(-5)+ =9,因此
图象经过点C (-5,9).
同理当x=-6时,y=- x+ =- ×(-6)+
= ≠10,
因此图象不经过点D (-6,10).
小试牛刀
判断某点是否在函数的图象上的方法:将该点的横坐标代入函数解析式,看求出的函数值是否等于纵坐标.若相等,则该点在函数的图象上;反之,则该点不在函数的图象上.
方法总结:
小试牛刀
5 已知函数y 与自变量x 之间成反比例关系,下表给出了
x 与y 的一些值:
(1)写出这个函数的解析式;
(2)根据函数解析式计算当x 的取值分别是-6和5时的函数值,
计算函数值分别是-12和36时的自变量的值.
x … -3 -2 -1 1 2 3 …
y … 1 2 4 -4 -2 -1 …
小试牛刀
(1)由表中的数据可知xy=-2,
所以函数的解析式是y=- .
(2)当x=-6时,函数值y=- = .
当x=5时,函数值y=- .
因为y=- ,所以x=- .
因此当y=-12时,x=- = .
当y=36时,x=- =- .
解:
小试牛刀
6 一个小球由静止开始从一个斜坡上向下滚动,滚动的
距离s (m)与时间t (s)之间的函数解析式为s=2t 2(t ≥0).
(1)根据解析式完成下表,并画出图象;
(2)当小球滚动6.5 s时,其滚动的距离是多少?
(3)经过多少秒,小球滚动的距离是128 m
时间t/s 1 2 3 4
距离s/m
2
8
18
32
小试牛刀
(1)这个函数的图象如图.
(2)当t=6.5时,s=84.5,即当小球滚动6.5 s时,其
滚动的距离是84.5 m.
(3)当s=128时,t=8,即经过8 s,小球滚动的距离
是128 m.
解:
小试牛刀
如图,点P 是 ABCD 边上一动点,沿A→D→C→B 的路径移动,
设P 点经过的路径长为x,△BAP 的面积是y,则下列能大致反映
y 与x 的函数关系的图象是( )
A
课堂小结
课堂小结
函数的表示方法共有三种:
列表法、解析式法、图象法,它们分别从数、
式和形的角度反映了函数的本质.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
