【班海精品】人教版(新)八下-19.2 一次函数 第六课时【优质课件】
文档属性
| 名称 | 【班海精品】人教版(新)八下-19.2 一次函数 第六课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 10:20:43 | ||
图片预览









文档简介
(共40张PPT)
19.2 一次函数
第6课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
我们知道,世界各国温度的计量单位尚不统一,常用的有摄氏温度(℃)和华氏温度(℉)两种.它们之问的换算关系如下表所示:
摄氏温度/℃ … -10 0 10 20 30 …
华氏温度/℉ … 14 32 50 68 86 …
观察上表,如果把表中的摄氏温度与华氏温度都看作变量,那么它们之间的函数关系是一次函数吗
新课精讲
探索新知
1
知识点
建立一次函数模型解实际问题
在日常生活和生产实践中有不少问题的数量关系可以用一次函数来刻画.在运用一次函数解决实际问题时,首先判定问题中的两个变量之间是不是一次函数关系.当确定是一次函数关系时,可求出解析式,并运用一次函数的图象和性质进一步求得我们所需要的结果.
探索新知
确定两个变量是否构成一次函数关系的一种常用方法就是利用图象去获得经验公式,这种方法的基本步骤是:
(1)通过实验、测量获得数量足够多的两个变量的对应值;
(2)建立合适的直角坐标系,在坐标系内以各对应值为坐标描点,并用描点法画出函数图象;
(3)观察图象特征,判定函数的类型.这样获得的函数解析式有时是近似的.
探索新知
“建模”可以把实际问题转化为关于一次函数的数学问题,它的关键是确定函数与自变量之间的解析式,并确定实际问题中自变量的取值范围.
总 结
探索新知
例1
“黄金1号”玉米种子的价格为5元/kg.如果一次购买2 kg以上的种子,超过2 kg部分的种子价格打8折.
(1)填写表.
(2)写出付款金额关于购买量的函数解析式,并画出函数
图象.
购买量/kg 0.5 1 1.5 2 2.5 3 3.5 4 …
付款金额/元 …
探索新知
付款金额与种子价格相关. 问题中种子价格不是固定不变的,它与购买量有关. 设购买x kg种子,当0≤x≤2时,种子价格为5元/kg;当x>2时,其中有2kg种子按5元/kg计价,其余的(x-2)kg(即超出2 kg部分) 种子按4元/kg (即8折)计价,因此,写函数解析式与画函数图象时,应对 0≤x≤2和x>2分段讨论.
分析:
探索新知
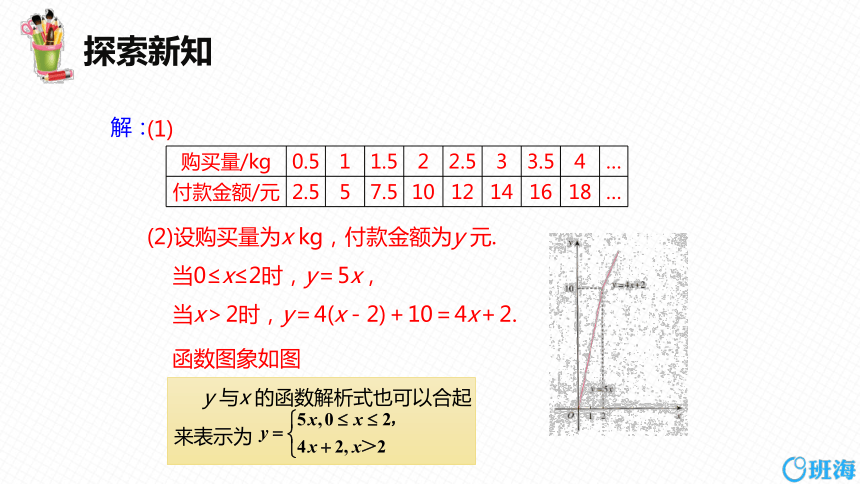
(1)
解:
购买量/kg 0.5 1 1.5 2 2.5 3 3.5 4 …
付款金额/元 2.5 5 7.5 10 12 14 16 18 …
(2)设购买量为x kg,付款金额为y 元.
当0≤x≤2时,y=5x,
当x>2时,y=4(x-2)+10=4x+2.
函数图象如图
y 与x 的函数解析式也可以合起
来表示为
探索新知
表格信息题是中考的热点题,解决表格问题的关键是从表格中获取正确、易于解决问题的信息;其建模的过程是:先设出函数的解析式,然后找出两对对应值,列出二元一次方程组,求解即可得到解析式.
总 结
典题精讲
1
小东家与学校之间是一条笔直的公路,早饭后,小东步行前往学校,途中发现忘带画板,停下给妈妈打电话,妈妈接到电话后,带上画板马上赶往学校,同时小东沿原路返回,两人相遇后,小东立即赶往学校,妈妈沿原路返回16 min到家,再过5 min小东到达学校,小东始终以100 m/min的速度步行,小东和妈妈的距离y(单位:m)与小东打完电话后的步行时间t(单位:min)之间的函数关系如图所示,下列四种说法:
典题精讲
①打电话时,小东和妈妈的距离为1 400 m;
②小东和妈妈相遇后,妈妈回家的速度为50 m/min;
③小东打完电话后,经过27 min到达学校;
④小东家离学校的距离为2 900 m.
其中正确的有( )
A.1个
B.2个
C.3个
D.4个
D
典题精讲
2
一旅游团来到黄冈某旅游景点,看到售票处旁边的公告栏如图所示,请根据公告栏内容回答下列问题:
公告栏
各位游客,本景点门票价格如下:
1.一次购买10张以下(含10张),每张门票180元;
2.一次购买10张以上,超过10张的部分,每张门票6折优惠.
典题精讲
(1)若旅游团人数为9人,门票费用是________元;
若旅游团人数为30人,门票费用是________元;
(2)设旅游团人数为x人,写出该旅游团门票费用y
(元)与人数x (人)的函数关系式(直接填写在下面
的横线上).
y=
_________(x=1,2,…,10), _____________ (x >10,且x 为整数).
1620
3960
180x
180x+720
探索新知
2
知识点
用一次函数解含图象的实际问题
思考
你能由上面的函数解析式解决以下问题吗?由函数图象也能解决这些问题吗?
(1)一次购买1.5 kg种子,需付款多少元?
(2)一次购买3 kg种子,需付款多少元?
探索新知
利用函数方法解决实际问题,关键是分析题中的数量关系,联系实际生活及以前学过的内容,将实际问题抽象、升华为一次函数模型,即建模,再利用函数的性质解决问题.一次函数的应用主要有两种类型:
(1)给出了一次函数解析式,直接应用一次函数的性质解决问题;
(2)只用语言叙述或用表格、图象提供一次函数的情境时,应先求出解析式,进而利用函数性质解决问题.
归 纳
探索新知
例2
某移动公司采用分段计费的方法
来计算话费,月通话时间x (min)
与相应话费y (元)之间的函数图象
如图.
(1)分别求出当0≤x<100和x≥100
时,y 与x 之间的函数解析式.
(2)月通话为280 min时,应交话费多少元?
导引:
本题是一道和话费有关的分段函数问题,通过图象可以
观察到,当0≤x<100时,y 与x 之间是正比例函数关系;
当x ≥100时,y 与x 之间是一次函数关系,分别用待定系
数法可求得它们的解析式.
探索新知
(1)当0≤x<100时,设y1=k1x (k1≠0),
将(100,40)代入得100k1=40,解得k1=
所以正比例函数的解析式为
当x ≥100时,设y2=k2x+b (k2≠0),
将(100,40)及(200,60)分别代入得
所以一次函数解析式为
解:
探索新知
因为280>100,
所以将x=280代入 中,得
即月通话时间为280 min时,应交话费76元.
解:
(2)月通话为280 min时,应交话费多少元?
探索新知
分段函数中,自变量在不同的取值范围内的解析式不同,在解决问题时,要特别注意自变量的取值范围的变化.分段函数的应用面广,在水费、电费、商品促销等领域都有广泛应用.本题考查一次函数及识图能力,体现了数形结合思想.解决问题的关键是由图象挖掘出有用的信息,利用待定系数法先求出函数解析式,再解决问题.
总 结
典题精讲
1
明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S (单位:m2)与工作时间t (单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )
A.300 m2 B.150 m2
C.330 m2 D.450 m2
B
典题精讲
2
为增强学生体质,某中学在体育课中加强了学生的长跑训练.在一次女子800米耐力测试中,小静和小茜在校园内200米的环形跑道上同时起跑,同时到达终点.所跑的路程s (米)与所用的时间t (秒)之间的函数图
象如图所示,则她们第一
次相遇的时间是起跑后的
第________秒.
120
易错提醒
汽车由A地驶往相距400 km的B地,如果汽车的平均速度是100 km/h,那么汽车距B地的距离s (km)与行驶时间t (h)的关系用图象表示应为( )
C
易错点:对自变量或函数值代表的实际意义理解不准确
而造成错误.
易错提醒
本题中s 并不是汽车行驶的路程,而是汽车距B 地的距离,不能被思维定式所左右,要仔细弄清题目,理解题意.实际上s 与t 的函数关系式为s=400-100t,其中0≤t≤4,s 是t 的一次函数,故选C.
学以致用
小试牛刀
1
一食堂需要购买盒子存放食物,盒子有A,B 两种型号,单个盒子的容量和价格如表.现有15升食物需要存放且要求每个盒子要装满,由于A 型号盒子正做促销活动:购买三个及三个以上可一次性返还现金4元,则购买盒子所需要最少费用为________元.
型号 A B
单个盒子容量/升 2 3
单价/元 5 6
29
小试牛刀
某蓝莓种植生产基地产销两旺,采摘的蓝莓部分加工销售,部分直接
销售,且当天都能销售完,直接销售是40元/斤,加工销售是130元/斤
(不计损耗).已知基地雇佣20名工人,每名工人只能参与采摘和加工中
的一项工作,每人每天可以采摘70斤或加工35斤,设安排x 名工人采摘
蓝莓,剩下的工人加工蓝莓.
(1)若基地一天的总销售收入为y 元,求y 与x 的函数关系式.
(2)试求如何分配工人,才能使一天的销售收入最大.并求出最大值.
小试牛刀
(1)根据题意得y=[ 70x-(20-x )×35]×40+(20-x )×35
×130=-350x+63 000.
∴y 与x 的函数关系式为y=-350x+63 000.
(2)∵70x ≥35(20-x ),∴x ≥ .
∵x 为正整数,且x ≤20,∴7≤x≤20,且x 为整数.
∵y=-350x+63 000中k=-350<0,
∴y 的值随x 的值的增大而减小,∴当x=7时,y 取最
大值,最大值为-350×7+63 000=60 550.
答:安排7名工人进行采摘,13名工人进行加工,
才能使一天的收入最大,最大收入为60 550元.
解:
小试牛刀
某快递公司的每位“快递小哥”日收入与每日的派送量成一次
函数关系,如图所示.
(1)求每位“快递小哥”的日收入y (元)与日派送量x (件)之间的
函数关系式;
(2)已知某“快递小哥”的日收入不少于110元,则他至少要派
送多少件?
小试牛刀
(1)设每位“快递小哥”的日收入y (元)与日派送量x (件)之
间的函数关系式为 y=kx+b,将(0,70),(30,100)
代入 y=kx+b,
得 解得:
∴每位“快递小哥”的日收入y (元)与日派送量x (件)之
间的函数关系式为 y=x+70.
(2)根据题意得:x+70≥110,解得:x ≥40.
∴他至少要派送40件.
解:
小试牛刀
4 某班级45名同学自发筹集到1 700元资金,用于初中毕业时各项活动的经费.通过商议,决定拿出不少于544元但不超过560元的资金用于请专业人士拍照,其余资金用于给每名同学购买一件文化衫或一本制作精美的相册作为纪念品.已知每件文化衫28元,每本相册20元.
(1)设用于购买文化衫和相册的总费用为W 元,求总费用W (元)与购买的文化衫件数t (件)的函数关系式.
(2)购买文化衫和相册有哪几种方案?为了使拍照的资金更充足,应选择哪种方案?并说明理由.
小试牛刀
(1)根据题意得:W=28t+20×(45-t )=8t+900.
(2)根据题意得:
解得:30≤t≤32,∴有三种购买方案:
方案一:购买30件文化衫、15本相册;
方案二:购买31件文化衫、14本相册;
方案三:购买32件文化衫、13本相册.
∵W=8t+900中W 随t 的增大而增大,
∴当t=30时,W 取最小值,此时用于拍照的费用最多.
∴为了使拍照的资金更充足,应选择方案一:购买30
件文化衫、15本相册.
解:
小试牛刀
“五·一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租
用新能源汽车自驾出游.根据如图所示的信息,解答下列问题:
(1)设租车时间为x 小时,租用甲公司的车所需费用为y1元,租用乙
公司的车所需费用为y2元,分别求出y1,y2关于x 的函数表达式;
(2)请你帮助小明计算并选择哪个出游方案合算.
小试牛刀
(1)设y1=k1x+80,
把点(1,95)代入,可得95=k1+80,
解得k1=15,
∴y1=15x+80(x ≥0);
设y2=k2x,把(1,30)代入,可得30=k2,
即k2=30,
∴y2=30x (x ≥0).
解:
小试牛刀
(2)当y1=y2时,15x+80=30x,解得x= ;
当y1>y2时,15x+80>30x,解得x< ;
当y1<y2时,15x+80<30x,解得x> ;
∴当租车时间为 小时时,选择甲乙公司一样合算;
当租车时间小于 小时时,选择乙公司合算;
当租车时间大于 小时时,选择甲公司合算.
课堂小结
课堂小结
运用一次函数解决实际问题的方法:
在日常生活和生产实践中有不少问题的数量关系可以用一次函数来刻画.在运用一次函数解决实际问题时,首先判断问题中的两个变量之间是不是一次函数关系,当确定是一次函数关系时,求出函数解析式,并运用一次函数的图象和性质进一步求得所需的结果.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
19.2 一次函数
第6课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
我们知道,世界各国温度的计量单位尚不统一,常用的有摄氏温度(℃)和华氏温度(℉)两种.它们之问的换算关系如下表所示:
摄氏温度/℃ … -10 0 10 20 30 …
华氏温度/℉ … 14 32 50 68 86 …
观察上表,如果把表中的摄氏温度与华氏温度都看作变量,那么它们之间的函数关系是一次函数吗
新课精讲
探索新知
1
知识点
建立一次函数模型解实际问题
在日常生活和生产实践中有不少问题的数量关系可以用一次函数来刻画.在运用一次函数解决实际问题时,首先判定问题中的两个变量之间是不是一次函数关系.当确定是一次函数关系时,可求出解析式,并运用一次函数的图象和性质进一步求得我们所需要的结果.
探索新知
确定两个变量是否构成一次函数关系的一种常用方法就是利用图象去获得经验公式,这种方法的基本步骤是:
(1)通过实验、测量获得数量足够多的两个变量的对应值;
(2)建立合适的直角坐标系,在坐标系内以各对应值为坐标描点,并用描点法画出函数图象;
(3)观察图象特征,判定函数的类型.这样获得的函数解析式有时是近似的.
探索新知
“建模”可以把实际问题转化为关于一次函数的数学问题,它的关键是确定函数与自变量之间的解析式,并确定实际问题中自变量的取值范围.
总 结
探索新知
例1
“黄金1号”玉米种子的价格为5元/kg.如果一次购买2 kg以上的种子,超过2 kg部分的种子价格打8折.
(1)填写表.
(2)写出付款金额关于购买量的函数解析式,并画出函数
图象.
购买量/kg 0.5 1 1.5 2 2.5 3 3.5 4 …
付款金额/元 …
探索新知
付款金额与种子价格相关. 问题中种子价格不是固定不变的,它与购买量有关. 设购买x kg种子,当0≤x≤2时,种子价格为5元/kg;当x>2时,其中有2kg种子按5元/kg计价,其余的(x-2)kg(即超出2 kg部分) 种子按4元/kg (即8折)计价,因此,写函数解析式与画函数图象时,应对 0≤x≤2和x>2分段讨论.
分析:
探索新知
(1)
解:
购买量/kg 0.5 1 1.5 2 2.5 3 3.5 4 …
付款金额/元 2.5 5 7.5 10 12 14 16 18 …
(2)设购买量为x kg,付款金额为y 元.
当0≤x≤2时,y=5x,
当x>2时,y=4(x-2)+10=4x+2.
函数图象如图
y 与x 的函数解析式也可以合起
来表示为
探索新知
表格信息题是中考的热点题,解决表格问题的关键是从表格中获取正确、易于解决问题的信息;其建模的过程是:先设出函数的解析式,然后找出两对对应值,列出二元一次方程组,求解即可得到解析式.
总 结
典题精讲
1
小东家与学校之间是一条笔直的公路,早饭后,小东步行前往学校,途中发现忘带画板,停下给妈妈打电话,妈妈接到电话后,带上画板马上赶往学校,同时小东沿原路返回,两人相遇后,小东立即赶往学校,妈妈沿原路返回16 min到家,再过5 min小东到达学校,小东始终以100 m/min的速度步行,小东和妈妈的距离y(单位:m)与小东打完电话后的步行时间t(单位:min)之间的函数关系如图所示,下列四种说法:
典题精讲
①打电话时,小东和妈妈的距离为1 400 m;
②小东和妈妈相遇后,妈妈回家的速度为50 m/min;
③小东打完电话后,经过27 min到达学校;
④小东家离学校的距离为2 900 m.
其中正确的有( )
A.1个
B.2个
C.3个
D.4个
D
典题精讲
2
一旅游团来到黄冈某旅游景点,看到售票处旁边的公告栏如图所示,请根据公告栏内容回答下列问题:
公告栏
各位游客,本景点门票价格如下:
1.一次购买10张以下(含10张),每张门票180元;
2.一次购买10张以上,超过10张的部分,每张门票6折优惠.
典题精讲
(1)若旅游团人数为9人,门票费用是________元;
若旅游团人数为30人,门票费用是________元;
(2)设旅游团人数为x人,写出该旅游团门票费用y
(元)与人数x (人)的函数关系式(直接填写在下面
的横线上).
y=
_________(x=1,2,…,10), _____________ (x >10,且x 为整数).
1620
3960
180x
180x+720
探索新知
2
知识点
用一次函数解含图象的实际问题
思考
你能由上面的函数解析式解决以下问题吗?由函数图象也能解决这些问题吗?
(1)一次购买1.5 kg种子,需付款多少元?
(2)一次购买3 kg种子,需付款多少元?
探索新知
利用函数方法解决实际问题,关键是分析题中的数量关系,联系实际生活及以前学过的内容,将实际问题抽象、升华为一次函数模型,即建模,再利用函数的性质解决问题.一次函数的应用主要有两种类型:
(1)给出了一次函数解析式,直接应用一次函数的性质解决问题;
(2)只用语言叙述或用表格、图象提供一次函数的情境时,应先求出解析式,进而利用函数性质解决问题.
归 纳
探索新知
例2
某移动公司采用分段计费的方法
来计算话费,月通话时间x (min)
与相应话费y (元)之间的函数图象
如图.
(1)分别求出当0≤x<100和x≥100
时,y 与x 之间的函数解析式.
(2)月通话为280 min时,应交话费多少元?
导引:
本题是一道和话费有关的分段函数问题,通过图象可以
观察到,当0≤x<100时,y 与x 之间是正比例函数关系;
当x ≥100时,y 与x 之间是一次函数关系,分别用待定系
数法可求得它们的解析式.
探索新知
(1)当0≤x<100时,设y1=k1x (k1≠0),
将(100,40)代入得100k1=40,解得k1=
所以正比例函数的解析式为
当x ≥100时,设y2=k2x+b (k2≠0),
将(100,40)及(200,60)分别代入得
所以一次函数解析式为
解:
探索新知
因为280>100,
所以将x=280代入 中,得
即月通话时间为280 min时,应交话费76元.
解:
(2)月通话为280 min时,应交话费多少元?
探索新知
分段函数中,自变量在不同的取值范围内的解析式不同,在解决问题时,要特别注意自变量的取值范围的变化.分段函数的应用面广,在水费、电费、商品促销等领域都有广泛应用.本题考查一次函数及识图能力,体现了数形结合思想.解决问题的关键是由图象挖掘出有用的信息,利用待定系数法先求出函数解析式,再解决问题.
总 结
典题精讲
1
明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S (单位:m2)与工作时间t (单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )
A.300 m2 B.150 m2
C.330 m2 D.450 m2
B
典题精讲
2
为增强学生体质,某中学在体育课中加强了学生的长跑训练.在一次女子800米耐力测试中,小静和小茜在校园内200米的环形跑道上同时起跑,同时到达终点.所跑的路程s (米)与所用的时间t (秒)之间的函数图
象如图所示,则她们第一
次相遇的时间是起跑后的
第________秒.
120
易错提醒
汽车由A地驶往相距400 km的B地,如果汽车的平均速度是100 km/h,那么汽车距B地的距离s (km)与行驶时间t (h)的关系用图象表示应为( )
C
易错点:对自变量或函数值代表的实际意义理解不准确
而造成错误.
易错提醒
本题中s 并不是汽车行驶的路程,而是汽车距B 地的距离,不能被思维定式所左右,要仔细弄清题目,理解题意.实际上s 与t 的函数关系式为s=400-100t,其中0≤t≤4,s 是t 的一次函数,故选C.
学以致用
小试牛刀
1
一食堂需要购买盒子存放食物,盒子有A,B 两种型号,单个盒子的容量和价格如表.现有15升食物需要存放且要求每个盒子要装满,由于A 型号盒子正做促销活动:购买三个及三个以上可一次性返还现金4元,则购买盒子所需要最少费用为________元.
型号 A B
单个盒子容量/升 2 3
单价/元 5 6
29
小试牛刀
某蓝莓种植生产基地产销两旺,采摘的蓝莓部分加工销售,部分直接
销售,且当天都能销售完,直接销售是40元/斤,加工销售是130元/斤
(不计损耗).已知基地雇佣20名工人,每名工人只能参与采摘和加工中
的一项工作,每人每天可以采摘70斤或加工35斤,设安排x 名工人采摘
蓝莓,剩下的工人加工蓝莓.
(1)若基地一天的总销售收入为y 元,求y 与x 的函数关系式.
(2)试求如何分配工人,才能使一天的销售收入最大.并求出最大值.
小试牛刀
(1)根据题意得y=[ 70x-(20-x )×35]×40+(20-x )×35
×130=-350x+63 000.
∴y 与x 的函数关系式为y=-350x+63 000.
(2)∵70x ≥35(20-x ),∴x ≥ .
∵x 为正整数,且x ≤20,∴7≤x≤20,且x 为整数.
∵y=-350x+63 000中k=-350<0,
∴y 的值随x 的值的增大而减小,∴当x=7时,y 取最
大值,最大值为-350×7+63 000=60 550.
答:安排7名工人进行采摘,13名工人进行加工,
才能使一天的收入最大,最大收入为60 550元.
解:
小试牛刀
某快递公司的每位“快递小哥”日收入与每日的派送量成一次
函数关系,如图所示.
(1)求每位“快递小哥”的日收入y (元)与日派送量x (件)之间的
函数关系式;
(2)已知某“快递小哥”的日收入不少于110元,则他至少要派
送多少件?
小试牛刀
(1)设每位“快递小哥”的日收入y (元)与日派送量x (件)之
间的函数关系式为 y=kx+b,将(0,70),(30,100)
代入 y=kx+b,
得 解得:
∴每位“快递小哥”的日收入y (元)与日派送量x (件)之
间的函数关系式为 y=x+70.
(2)根据题意得:x+70≥110,解得:x ≥40.
∴他至少要派送40件.
解:
小试牛刀
4 某班级45名同学自发筹集到1 700元资金,用于初中毕业时各项活动的经费.通过商议,决定拿出不少于544元但不超过560元的资金用于请专业人士拍照,其余资金用于给每名同学购买一件文化衫或一本制作精美的相册作为纪念品.已知每件文化衫28元,每本相册20元.
(1)设用于购买文化衫和相册的总费用为W 元,求总费用W (元)与购买的文化衫件数t (件)的函数关系式.
(2)购买文化衫和相册有哪几种方案?为了使拍照的资金更充足,应选择哪种方案?并说明理由.
小试牛刀
(1)根据题意得:W=28t+20×(45-t )=8t+900.
(2)根据题意得:
解得:30≤t≤32,∴有三种购买方案:
方案一:购买30件文化衫、15本相册;
方案二:购买31件文化衫、14本相册;
方案三:购买32件文化衫、13本相册.
∵W=8t+900中W 随t 的增大而增大,
∴当t=30时,W 取最小值,此时用于拍照的费用最多.
∴为了使拍照的资金更充足,应选择方案一:购买30
件文化衫、15本相册.
解:
小试牛刀
“五·一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租
用新能源汽车自驾出游.根据如图所示的信息,解答下列问题:
(1)设租车时间为x 小时,租用甲公司的车所需费用为y1元,租用乙
公司的车所需费用为y2元,分别求出y1,y2关于x 的函数表达式;
(2)请你帮助小明计算并选择哪个出游方案合算.
小试牛刀
(1)设y1=k1x+80,
把点(1,95)代入,可得95=k1+80,
解得k1=15,
∴y1=15x+80(x ≥0);
设y2=k2x,把(1,30)代入,可得30=k2,
即k2=30,
∴y2=30x (x ≥0).
解:
小试牛刀
(2)当y1=y2时,15x+80=30x,解得x= ;
当y1>y2时,15x+80>30x,解得x< ;
当y1<y2时,15x+80<30x,解得x> ;
∴当租车时间为 小时时,选择甲乙公司一样合算;
当租车时间小于 小时时,选择乙公司合算;
当租车时间大于 小时时,选择甲公司合算.
课堂小结
课堂小结
运用一次函数解决实际问题的方法:
在日常生活和生产实践中有不少问题的数量关系可以用一次函数来刻画.在运用一次函数解决实际问题时,首先判断问题中的两个变量之间是不是一次函数关系,当确定是一次函数关系时,求出函数解析式,并运用一次函数的图象和性质进一步求得所需的结果.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
