1.4等腰三角形 课件

课件14张PPT。1.4等边三角形知识回顾:(1).等边三角形的性质
1.等边三角形的内角都相等,且都等于60 °
2.等边三角形是轴对称图形，有三条对称轴
3.等边三角形各边上中线,高和所对角的平分线都三线合一.
1.三边相等的三角形是等边三角形.
2.三个内角都等于60 °的三角形是等边三角形.
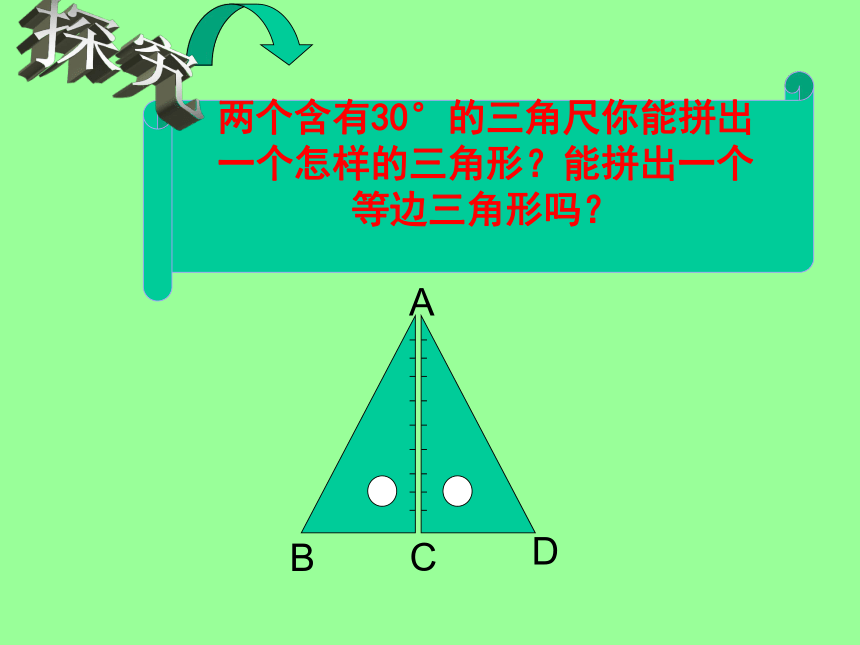
3.有一个内角等于60 °的等腰三角形是等边三角形.(2) 等边三角形的判定:两个含有30°的三角尺你能拼出
一个怎样的三角形？能拼出一个
等边三角形吗？
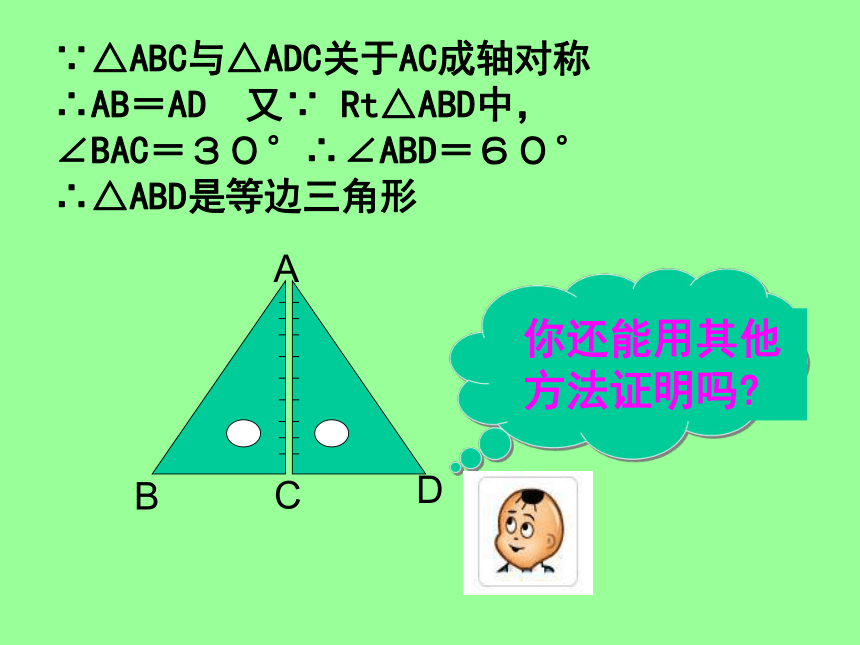
探究∵△ABC与△ADC关于AC成轴对称
∴AB＝AD　又∵ Rt△ABD中，
∠BAC＝３０°∴∠ABD＝６０°
∴△ABD是等边三角形
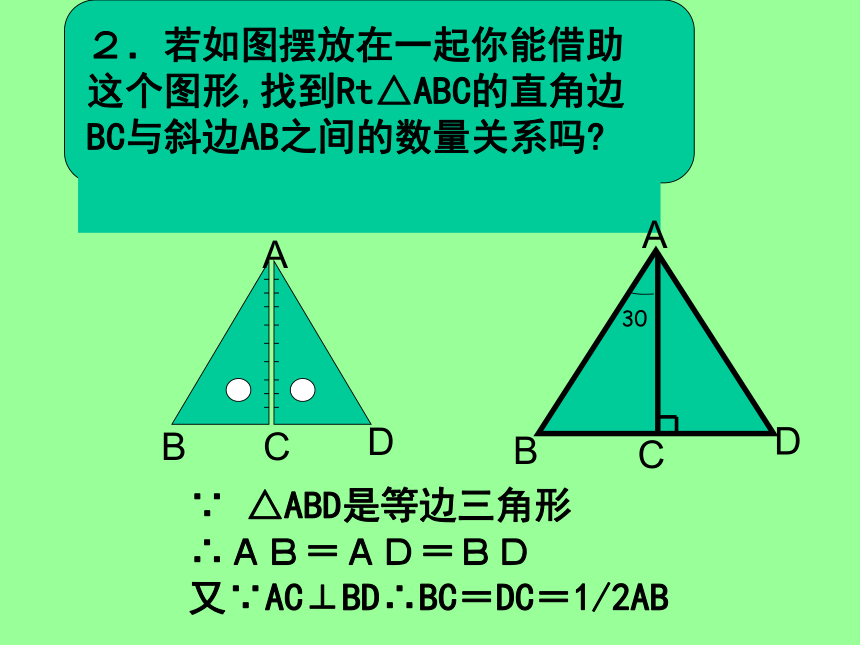
∵ △ABD是等边三角形
∴ＡＢ＝ＡＤ＝ＢＤ
又∵AC⊥BD∴BC＝DC＝1/2AB

定理：
在直角三角形中，如果一个锐角等30°，
那么，它所对的直角边等于斜边的一半。

即在Rt△ABC 中，如果
∠ＡＣB ＝ ９0° ∠A＝ 30 °
那么 ＢＣ＝１／２ＡＢ

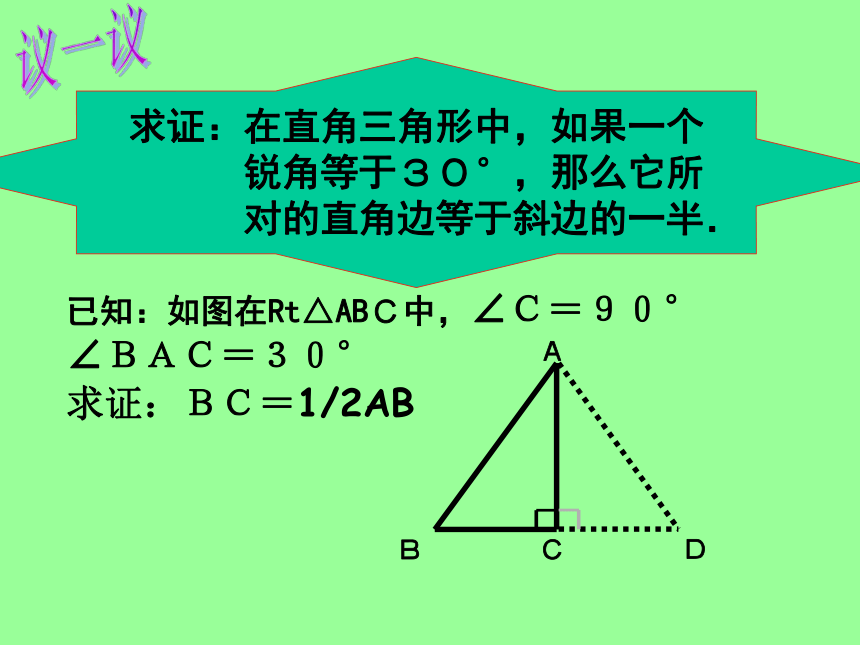
求证：在直角三角形中，如果一个
　　　锐角等于３０°，那么它所
　　　　对的直角边等于斜边的一半．已知：如图在Rt△ABＣ中，∠Ｃ＝９０°
∠ＢＡＣ＝３０°
求证：ＢＣ＝1/2AB
Ｄ议一议证明：延长BC至Ｄ，使CD＝BC，连接AD．
∵∠ACB＝90°∠BAC＝30°则∠Ｂ＝60°．
∵ ∠ACB＝90° ∴∠ACD＝90°
∵ AC＝AC ∴ △ABＣ≌△ADC（ＳＡＳ）
∴ AB=AD（全等三角形的对应边相等）
∴ △ABD是等边三角形（有一个角是60°的等腰三角形是等边三角形）．
∴ BC＝1/2BD＝1/2AB结论： 在直角三角形中，30°所对 的直角边等于斜边的一半。
在RT△ABC中
∵∠A＝30°
∴AC＝2BC
或BC＝1/2 AC语言转化
例5.右图是屋架设计图的一部分，点D是斜梁AB的中点，立柱BC、DE垂直于横梁AC，AB=7.4m, ∠A＝ 30 °,立柱BC、DE要多长？
解： ∵DE⊥AC，BC⊥AC， ∠A＝ 30 °
由上述定理可得：
BC=1/2AB，DE=1/2AD，
∴BC=1/2×7.4=3.7(m)
又AD=1/2AB,=
∴DE=1/2AD=1/2×3.7=1.85(m).
答：立柱BC、DE分别要3.7m、1.85m.
1在Rt△ABC 中， ∠Ｃ＝ ９0°，
∠B＝ 2 ∠Ａ，问∠B 、∠A各是多少度？
边AB与BC之间有什么关系？练习同学们：
“教”不等于“懂”
“懂” 不等于“会”，
“会”不等于“通”，
由“教”到“懂”需要“学”，
由“懂”到“会”需要“习”，
而由“会”到“通”则离不开“悟”。寄语 1 如图,在△ABC 中∠C=90°,∠B=15°,AB的垂直平分线交BC于D,交AB于M,且BD=8㎝,求AC之长.补充练习
2 如图,在△ABC 中,AB=AC, ∠A=120°,AB的垂直平分线
MN交BC于M,交AB于N,
求证:CM=2BM